遥感影像是信息的重要载体。近年来,随着计算机技术的发展,通过对遥感影像的分析处理,进而获得相关信息已成为诸多科研及工程领域研究、应用的一种重要模式[1,2],但其数据量庞大且具有一定冗余度,成为制约其应用的一大障碍。因此,一直以来,关于遥感影像数据的压缩编码及空间对象合并技术都是相关领域研究和关注的重点。
在诸多关于遥感影像压缩合并方法的研究中,四叉树原理以其优良的表现和简洁的编码过程一直以来都是一个重点的研究方向,而且相关的研究成果较多[3,4,5,6,7,8]。
关于四叉树原理的压缩研究主要分为两个研究重点:一个研究重点是研究在一定误差范围内,提高数据的压缩程度。这个问题上比较典型的有3个子方向:一是各种自适应判别谓词的改进,如倪林提出一种自适应四叉树分割处理方法,有效提高了遥感图像的压缩比[4];二是引入新的理论对分割结果进行优化[6];三是分割形状的改进[5]。另一个研究重点是研究如何提高压缩过程效率。这个问题的主要研究内容是将四叉树自上而下的递归构建过程改为自底至上的线性编码过程,以及对这种线性编码过程进行优化[3]。
诸多研究工作者在这两个问题的研究上取得了显著的成果。但其中也有一些尚待研究的问题,如在诸多相关研究文献中,基于四叉树原理的遥感影像处理研究大都是基于单一波段的灰度图像。而在对于遥感影像数据的分析研究中大都是基于多个波段的影像进行的。另外,四叉树算法由于其原理的特性,会在数据分块压缩过程中产生过度分割现象,但在相关文献中,对于这个问题的解决却很少涉及。
本文针对以往研究中存在的这两点待改进之处,提出一种基于四叉树原理的多波段遥感图像区域合并有损压缩算法。该算法能够将多波段的遥感图像数据进行区域合并,经试验验证,比传统的四叉树算法具有更高的压缩比。
一、 多波段遥感图像的区域合并算法 1. 经典四叉树算法原理在介绍本文算法之前,首先来简要介绍一下经典的四叉树算法原理。四叉树是一种树形数据结构,它的每个节点下可以有4个子节点或没有子节点(如图 1所示)。

|
| 图 1 四叉树示意图 |
在构建图像四叉树编码的过程中,算法首先要设立一个判断谓词,以对节点区域是否需要继续分割进行判断;而后将原始数据作为根节点,判断节点是否可以继续分割,若满足继续分割条件,则将节点区域分为4组相同的象限;而后对4组象限继续迭代执行判断分割过程,直到所分节点区域不满足继续分割条件而终止(如图 2所示)。

|
| 图 2 四叉树图像压缩示意图 |
从算法原理上看,四叉树的构造过程本质是递归构造,这在算法实现的过程中具有编码简洁、易于理解等优点。
下面本文将对所提出的改进算法进行详细的阐述。
2. 针对多波段图像的判别谓词设计通过上一节关于经典四叉树算法原理的介绍可以看出,在对数据进行四叉树处理的过程中,首先就是要确定区域可分割条件,即判别谓词。对于单一波段遥感影像,其可用以下形式表示
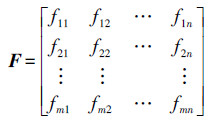
式中,fij为坐标为(i,j)的像元的灰度值。这种情况下,四叉树的判别谓词基本上都是对区域灰度值的一些统计信息的一些判别。而多波段图像中,每一个像元在每个波段上都有一个对应的属性值,这使得对其可分割条件的确定造成了一定的困难。
在此,引入“属性空间”这一概念,即将任一像元所对应的各波段的属性值看作该像元所对应的属性向量,对于k个波段的遥感影像可表示为
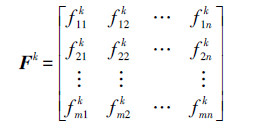
式中,像元(i,j)的属性为一个k维向量,向量的每一维分量对应着该像元的一个波段的属性值。
引入属性空间概念后,一个区域内的像元属性即可看作是属性空间中分布的一些离散点。由灰度图像处理中的判别谓词设计方式很容易联想到,此时,对于判别谓词可以设计为针对这些属性点的某些统计信息的判别。
在对于灰度图像的四叉树分解中,比较常用的一种判别方案是对区域灰度级差的阈值判别,即若区域内灰度最大值与最小值的差大于预设阈值,即判定此区域为非同质区域,需要继续对其进行分解;否则判定为同质区域,保留区域为四叉树的一个叶节点。在“属性空间”的统一表达之下,这种灰度值的级差可以用区域内属性点的最远点距代替。因此,本文所采用的判别谓词为区域内属性点中最远点对的绝对值距离与预设阈值的大小比较,若最远点距大于阈值,则区域需要继续分割;若小于阈值,则保留区域为四叉树的一个叶节点。即对于区域Fk,通过判断
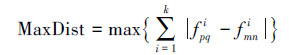
与预设阈值的大小关系,来判定区域是否继续分割。其中,p-m≥0,q-n≥0,且p-m和q-n不同时为0。
确定了判别条件之后,需要设计一套具有可行性的具体方案。由于遥感数据的海量特性,在对其中某个区域进行最远点距计算的过程中不可能采用暴力搜索的方式。本文采取的办法是首先求出区域属性点的凸包点集,属性点中的最远点对显然会产生在凸包点集内。因此,只需要计算凸包点集中最远点对的距离,即可求得区域属性点中的最远点对距离。
在求区域属性点凸包点集的过程中,有一点需要注意,即对于多波段的遥感影像数据,其属性点都是多维的,而某区域内属性点在属性空间中的分布形态维度有可能会与属性空间维度不同,如三维空间中的共面分布或共线分布的离散点。而产生最远点距的凸包点集显然是针对于分布形态下的凸包点集,且对于不同维度的离散点数据,求取凸包点集的过程是有所差别的。因此,在求区域属性点凸包点集之前,需要首先对属性点的分布形态进行确定,而后再针对分布形态,求其凸包点集,并进行最远点距的计算。
对于区域属性点分布形态的确定,本文采用如下策略,以三维数据为例,某区域内的属性点可以表示为
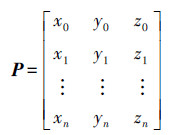
式中,矩阵中每一行代表一个属性点数据,每一列分别代表不同波段。对于属性点集P,首先将其中第一个点移至原点,其余点作相应移动,去掉原点后,得到新点集P′,如下所示

由相关知识易知,原始点集的分布形态维度与新点集矩阵P′的秩相同,即若原始点集呈三维形态分布,则矩阵P′的秩为3;若呈二维形态分布(共面分布),则矩阵P′的秩为2,以此类推。
因此,可以通过取矩阵P′的一个列极大线性无关组来选取对确定属性点位置有独立贡献的分量。那么,就可以通过取原始点集P中的对应列分量,将原始点集投影到相应维度的空间,由选取条件保证,点集分布形态的维度与投影空间的维度必然相等。因此,可以在投影空间中求出凸包点集,再将其对应到原始点集求出属性点的最远点对距离。
采用以上一整套执行方案,不仅可以在多波段遥感影像区域分割条件判别过程中避免错误,还能够极大限度地减少判别过程的运算量,提高程序的效率。
3. 基于四叉树原理的区域合并算法(1)数据结构设计
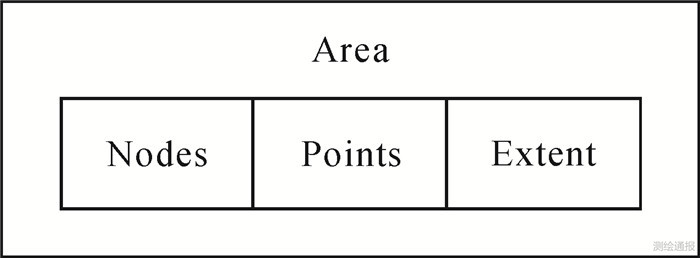
在上文关于经典四叉树原理的介绍中得知,四叉树算法在处理图像数据过程中,在具有相应优势的同时,也存在着过度分割的现象。本文针对这种不足,设计出如图 3所示的数据结构,用于在四叉树处理遥感数据过程中进行区域合并操作。
|
| 图 3 区域数据结构示意图 |
该结构分为3个部分:第一部分称为Nodes,用于存储Area结构内每个四叉树叶节点的上下左右四边界在图中的位置;第二部分称为Points,用于存储对应叶节点内原始像元的属性向量;第三部分称为Extent,用于存储整个Area结构的四方边界位置。
对于这种结构,本文的使用方式为在四叉树分割构建过程中,对于不满足可继续分割的叶节点,首先将其按Area结构进行存储。由于经典的四叉树构建为一种自顶至下的迭代过程,因此在其分割完成之后,必然会存在一个自底至上的返回值过程,其返回的值即为本次迭代区域的四叉树编码序列。本文正是基于这种自底至上返回过程的存在,设计出一种在返回值阶段的区域合并策略。
(2)合并方案设计
首先,对于不满足继续分割条件的区域,算法会自动将其按Area结构进行存储,即在递归过程的最底层,算法可以获得最基础的Area结构对象。这些Area结构对象将会被返回到递归的上一层。本文所提出的区域合并过程,就是从算法接收到由下层递归返回的基础Area结构开始进行的。而这种接收下层返回、合并、返回上一层的模式将一直进行到四叉树的根节点层,以完成全部输入数据的区域合并操作。
确定整体合并过程模式之后,本文重点介绍算法合并环节的具体执行策略。由于算法的合并环节位于四叉树递归的返回值阶段之前,因此,对于任意一个非叶节点,它所接收到的下层返回值都是本节点区域4个象限内已经完成合并的Area结构集合。因此,在本节点将Area结构集合返回给上层节点之前,需要完成本节点内的区域合并任务,而本节点的区域合并任务,即为横纵两条分界线上的Area结构的合并。
具体的合并策略如下,以横向分界线为例。
①获取相关元素集合
首先,搜索Area集合中Extent上界和下界落在分界线位置的元素,会得到两个Area结构的集合
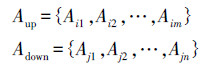
式中,第一个集合为分界线上方,区域下边界落在分界线上的Area结构集合;第二个集合为分界线下方,区域上边界落在分界线上的Area结构集合。由于Area结构中可能存在多个叶节点,而不是每个叶节点都与分界线相邻,因此,为尽可能减小计算量,需要从两个Area集合中选出相应边界落在分界线上的叶节点,可以得到相应的两个叶节点的集合
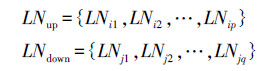
式中,第一个集合为分界线上方,下边界落在分界线上的四叉树叶节点集合;第二个集合为分界线下方,上边界落在分界线上的四叉树叶节点集合。
②合并
获取分界线上的叶节点集合之后,分别对两个集合中的叶节点按其节点左边界进行集合内排序,然后从左至右对两集合中的叶节点进行合并判断。
合并判断的过程如下:
a.首先判断两个叶节点是否邻接,判别的方法为判断表达式
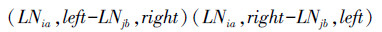
与0的大小,若表达式小于等于0,则两叶节点邻接;否则,两叶节点不邻接。若两个叶节点不相邻,则将右边界较小的叶节点用其右侧相邻的节点代替,继续判断节点相邻;若两节点相邻,则进行下一步。
b.对于相邻叶节点,取两个叶节点所在Area的Points部分,计算两个Area结构的属性点最远点距,判断其是否小于阈值。
若小于阈值,则证明两个Area结构可以合并,将这两个Area结构的ID记录下来。记录ID的目的是用于全部判断完毕之后的合并操作,以及防止有相同Area的重复合并。
若最远点距不小于阈值,证明两个Area不满足合并条件,则在两个叶节点集合中,右边界较小的节点跳过与参与本次判断的叶节点相邻的同Area节点,而后返回步骤1)进行节点相邻判断。
c.完成全部判断之后,按记录的可合并Area结构对Area结构进行合并。
(3)算法流程
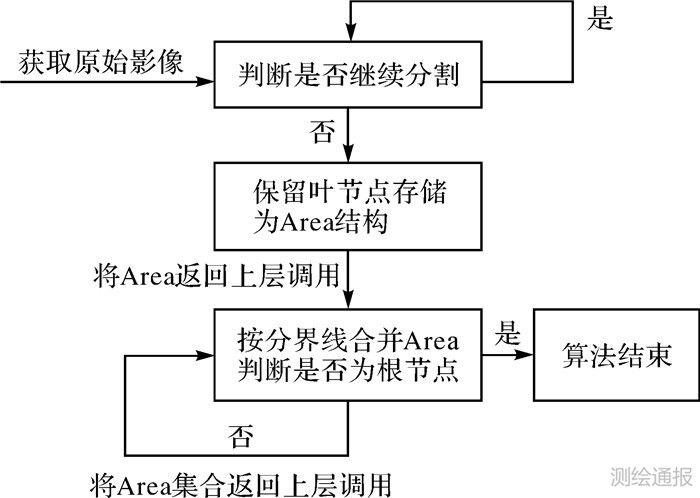
综上所述,本文所提出的多波段遥感影像的区域合并算法流程如图 4所示。
|
| 图 4 本文算法流程 |
如图 4所示,本文算法主要步骤如下:
1)获取原始影像数据,根据判别方案判断区域是否需要分割:①若满足分割条件,将区域四分,重复迭代步骤1);②若不满足分割条件,将区域保留为叶节点,并存储为Area结构,返回给迭代上层。
2)将接收到的下层Area集合返回值按本层分界线进行合并,并判断是否为根节点:①若不是根节点,则将Area结构集合返回给迭代上层,重复迭代步骤2);②若是根节点,算法结束。
二、 试验结果及分析本文随机选取Landsat8卫星某区域1024×1024像素尺度的多波段遥感影像数据,将本文提出的区域合并算法与传统的四叉树算法进行对比试验。并通过对结果进行比较分析,阐述本文提出算法的优势。
本文所选数据波段为2、3、4、5、6共5个波段,由于波段数量较多,本文用其自然真彩色波段来展示试验区的直观概况,如图 5所示。

|
| 图 5 试验区真彩色波段遥感影像 |
在试验过程中,本文所采取的预设阈值策略为用区域整体属性点最远点距乘以一个精度系数作为算法阈值,系数不同则算法的精度也有相应的差异。试验所采取的具体系数为0.1、0.085、0.070、0.055、0.04、0.025、0.01共7种不同的精度。试验结果数据对比见表 1。
| 阈值精度 | 区域数量 | 压缩比 | 误差均值 | 误差变异系数 | ||||
| 传统方法 | 本文方法 | 传统方法 /(%) | 本文方法 /(%) | 传统方法 | 本文方法 | 传统方法 | 本文方法 | |
| 0.1 | 260 986 | 76 776 | 24.89 | 7.32 | 0.019 | 0.025 | 0.781 | 0.659 |
| 0.085 | 320 569 | 100 611 | 30.57 | 9.60 | 0.017 | 0.023 | 0.780 | 0.636 |
| 0.07 | 396 880 | 134 093 | 37.85 | 12.79 | 0.014 | 0.019 | 0.775 | 0.613 |
| 0.055 | 493 945 | 183 322 | 47.11 | 17.48 | 0.011 | 0.016 | 0.781 | 0.588 |
| 0.04 | 613 996 | 260 890 | 58.56 | 24.88 | 0.008 | 0.012 | 0.805 | 0.551 |
| 0.025 | 740 467 | 396 662 | 70.62 | 37.83 | 0.005 | 0.008 | 0.851 | 0.516 |
| 0.01 | 843 130 | 662 554 | 80.41 | 63.19 | 0.002 | 0.003 | 1.105 | 0.574 |
关于表 1有几点需要说明:
1)本文所选区域的原始数据量为区域像元数,即1024×1024像素=1 048 576像素。
2)本文在合并后的误差相关值计算都是以区域内属性均值代替区域内各像元属性值进行的。
3)表中的数据距平均值是将各个波段的属性值除以波段值范围(65 535)后的相应计算值。在各项数据中,误差均值反映出压缩后数据与原始数据误差的平均程度;误差变异系数反映出误差分布的稳定性。
从压缩比一项中可以看到,本文所选取的算法精度控制系数对数据的压缩范围基本涵盖了从低精度压缩到高精度压缩的有效范围,因此,这两组试验的参数选取是有意义的。
从表 1可以看出,两种算法在压缩程度和压缩精度方面都有不错的表现,压缩后的数据在概念上的数据量都有明显的减少,而且与原始数据的误差均值都能够保持在一个较小的范围内。传统的四叉树算法由于对数据的分割较细,因此在误差均值方面总体上比本文算法要略好一些。但是随着算法精度的提升,本文算法在误差均值方面逐渐减小的同时,其与传统四叉树在这方面的差异也在缩小。同时,通过对误差变异系数的对比可以看出,本文算法处理后的数据,其误差的分布较之传统四叉树算法都是相对稳定的,这种误差分布的稳定性优势也是不可忽视的一个方面。
下面,本文将两种算法的试验结果相关数据绘制成图,以便更直观地对两种算法的效果进行比较,如图 6-图 8所示
。
|
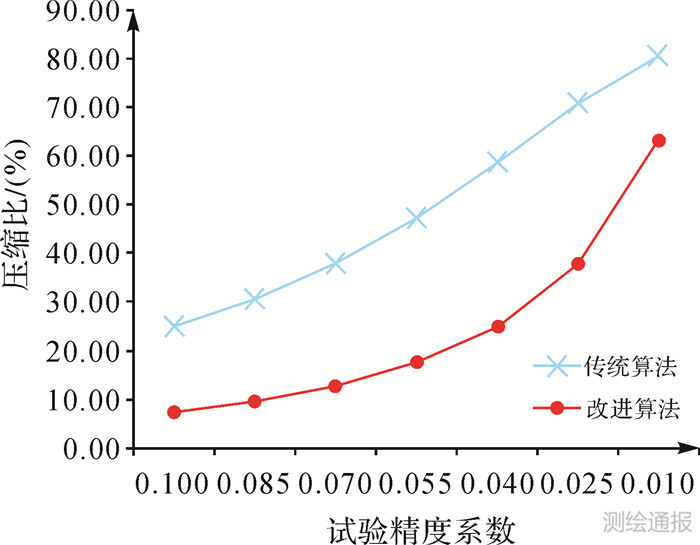
| 图 6 试验结果压缩比比较 |
通过以上3张试验结果数据比较图能够比较直观地看出,虽然随着算法精度的提升,两种算法在压缩程度上都有所减弱,但是本文算法与传统的四叉树算法相比,其在压缩程度上的表现是具有稳定性和明显优势的。由于无限高精度的压缩是无意义的,因此,在有意义的压缩精度范围内,本文算法在压缩程度上是明显优于传统的四叉树算法的。
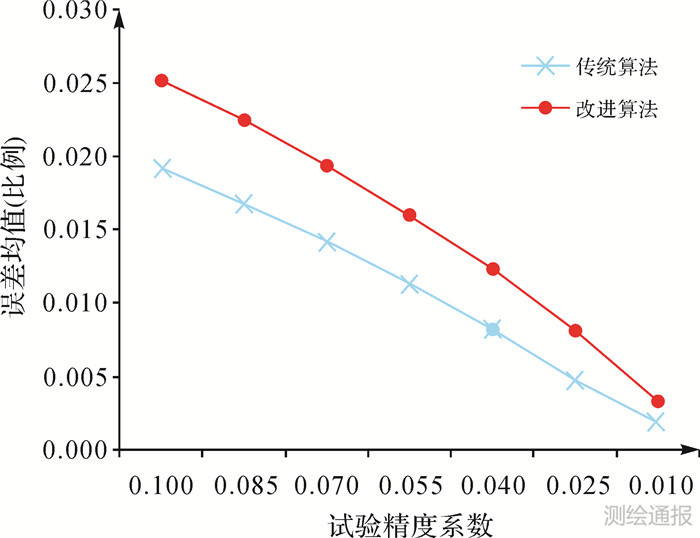
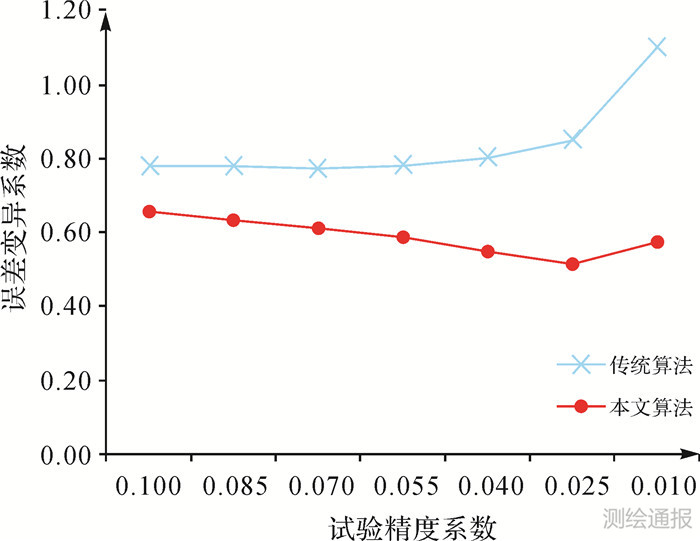
通过图 7可以看出,虽然本文算法在误差均值上比传统四叉树算法略有不足,但是,在算法精度达到某一个程度之后,这种差异是明显减弱的,而由于两种算法本身在误差方面的控制就相对比较出色,因此,在一定算法精度内,这种误差均值上的差异是可以忽略的。而且从图 8中也可以看出,传统四叉树算法在误差分布的稳定性上有明显的不足,而这种误差分布稳定性方面的不足会使相同精度下的数据信息丢失更多。与之相比,本文算法在误差分布上较之传统四叉树算法是相对稳定的。因而随着算法精度的提高,误差均值的差异逐渐减小,本文算法在误差分布稳定性上的优势会使原始数据信息量获得更大程度的保留。因此,从以上图表的分析中可以看出,从整体上来说,本文算法较之传统的四叉树压缩算法无论在压缩程度还是压缩精度上的表现都是具有较为明显优势的。
|
| 图 7 试验结果误差均值比较 |
|
| 图 8 试验结果误差变异系数比较 |
针对以往基于四叉树原理的数据压缩研究中存在的过度分割问题和多波段数据处理问题,本文首先引入“属性空间”这一概念,将多波段与单一波段数据进行统一化表达,而后针对四叉树算法的过程特点,在算法迭代返回前设计区域合并方案以弥补过度分割的问题。通过试验验证,对于多波段遥感影像数据的压缩去冗余过程,本文算法较之传统四叉树算法在压缩程度上有50%以上的提升,在误差控制上都有较为显著的优势。同时,由于本文算法可以对任意数量波段进行压缩合并处理,使其应用范围突破了以往的数据压缩存储局限,因而能够在基于遥感影像的相关分析处理中达到去除冗余信息、精简数据的目的。
致谢:感谢武汉大学资源与环境科学学院刘殿锋老师在论文撰写过程中给予的大力支持与帮助。
| [1] | 赵英时.遥感应用分析原理与方法[M].北京:科学出版社,2003. |
| [2] | 贾坤,李强子,田亦陈,等. 遥感影像分类方法研究进展[J].光谱学与光谱分析,2011,31(10):2618-2623. |
| [3] | 谢顺平,冯学智,王结臣,等.一种基于优势属性存储的四叉树结构及其构建算法[J].武汉大学学报(信息科学版),2009,34(6):663-666. |
| [4] | 倪林.基于自适应四叉树分割的遥感图像压缩算法[J].遥感学报,2002,6(5):343-351. |
| [5] | 范东光. 图像的自适应分解算法及应用研究[D].杭州:杭州电子科技大学,2013. |
| [6] | 周四龙,粱栋,王慧,等.基于四叉树与图割的遥感图像分割方法[J].计算机工程,2010,36(8):224-226. |
| [7] | ADAM S, PIER LUIGI D. Quadtree Structured Image Approximation for Denoising and Interpolation[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1226-1239. |
| [8] | CHEN H H, DING J J, SHEU H T. Image Retrieval Based on Quadtree Classified Vector Quantization[J]. Multimedia Tools and Applications, 2014, 72(2): 1961-1984. |


