近年来随着各种高分卫星的成功发射,QuickBird、IKONOS及国内的高分一号(GF1)、资源三号(ZY-3)等高分数据得到了广泛应用。然而,传感器在测量过程中若使获取的波段更窄则必须增大瞬时视场以采集更多的光,因此导致影像空间分辨率下降,光谱分辨率与空间分辨率很难同时兼具。如何充分发挥不同影像的优势,满足研究过程中对空间分辨率与光谱分辨率的需求,获取高质量的融合影像是当前遥感数据预处理的研究热点。传统的遥感影像融合方法主要以HIS变换[1]、主成分分析(principle component analysis,PCA)[2]、加权融合、Gram_Schimdt(GS)[3]变换法、空间局部相关法[4]等方法为主,这几种方法能够有效增强影像空间域信息,却不能很好地保持光谱信息。随着小波变换(wavelet transform)的出现,因其能够同时进行时间-频率局部分析,能有效反映一维函数的点奇异特性,然而对于高维影像的具有多方向性的纹理和边缘信息小波变换则不能很好地表示[5]。为了更好地处理高维影像,Do提出轮廓波变换(contourlet transform,CT)的多尺度几何分析方法,能够灵活地实现多尺度、多方向变换,但由于其存在下采样过程导致影像出现频域混叠,导致影像失真[6]。2006年Arthur等在Contourlet的基础上构建了一种基于非下采样的变换算法(nonsubsampled contourlet transform,NSCT),NSCT不仅具有多尺度多方向分解特性,同时还具备了平移不变性,可以很好地表示影像的边缘轮廓信息[7]。影像的纹理等细节信息在影像分类应用中十分关键,当影像存在较大噪声时,表现为高频信号,因此NSCT并不能很好地区分出纹理与噪声,为此本文提出采用方向信息测度[8]建立NSCT的高频系数融合规则,实现影像的多尺度多方向分割,同时有效抑制影像的噪声,较好的区分影像的边缘轮廓、纹理细节信息,实现影像融合的光谱信息和空间信息保真,并以GF1卫星的全色波段与多光谱波段融合进行试验,与常用的小波融合方法、GS变换融合法进行对比分析,验证本文方法的优势。
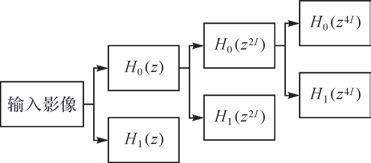
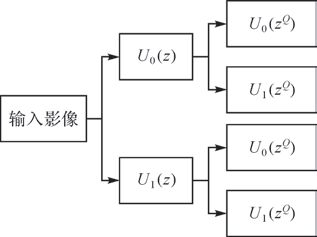
一、 数据与方法 1. NSCT变换原理NSCT很好地解决了因下采样产生的混频问题,能够快速实现多尺度、多方向扩展,有利于表示图像的边缘轮廓信息,因此在图像重建、医学影像信息检测等方面得到了有益的尝试,而在高分影像中的应用还需进一步探讨。NSCT主要是由非下采样金字塔(nonsubsampled pyramid,NSP)和非下采样方向滤波器组(nonsubsampled directional filter bank,NSDFB)构成,其原理首先是通过NSP对影像进行多尺度分解,以捕获影像“奇异点”,然后利用NSDFB对NSP分解的高频子带实现多方向分解,使“奇异点”连接成轮廓段,以此为基元逐步逼近原始影像。NSP是一个金字塔双通道滤波器组,通过NSP的一阶分解可以获得一个高频子带H0(z)及一个低频子带H1(z),同样还可以对高频子带按照2阶单位矩阵进行上采样生成次子带,从而实现输入影像的多尺度分解。如图 1所示即为一个3阶的NSP金字塔分解结构示意图,原始输入影像经过j阶分解后,可以生成j+1个与输入影像尺寸相同的频带,其中低通频带子带的理想支撑频域为[(-π/2j),(π/2j)]2,高通频带子带的理想支撑频域为[(-π/2j-1),(π/2j-1)]2\[(-π/2j),(π/2j)]2。NSDFB也是一组双通道的方向滤波器,经NSDFB分解后可得到两个不同方向的理想支撑频域U0(z)和U1(z),如图 2所示NSDFB不通过使用Contourlet Transform的向下重采样,而是通过其他各种采样矩阵对每一层的频域进行向上重采样,从而得到下一层的方向频域,实现输入影像的多方向分解。对第j层的高频子带影像进行k个方向的分解后,就可以得到2k个高频子带影像。
|
| 图 1 NSP金字塔3阶分解结构 |
|
| 图 2 NSDFB方向滤波器2阶分解结构 |
NSCT变换是通过NSP与NSDFB的分解与重构实现的,且分解滤波器和合成滤波器之间满足Bezout关系式(式(1)),因此经过j级NSCT变换后的影像,分解为1个低频子带及
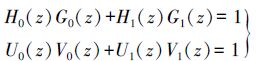 (1)
(1) 式中,H0(z)、G0(z)分别为NSP金字塔的分解、合成滤波器;U0(z)、V0(z)分别为NSDFB方向滤波器的分解、合成滤波器。
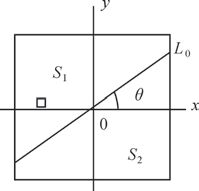
2. 方向信息测度原理在影像的细节信息表征中,影像的边缘和纹理通常都具有方向性,而噪声等不具有方向性,基于此,本文研究在NSCT频域分解的基础上,利用方向信息测度建立高频融合系数选取规则,提取影像的纹理轮廓信息并将其注入到融合影像中,将有利于恢复影像的空间细节等信息,同时还有利于抑制噪声[9]。方向信息测度是一种面向像素灰度值的方法,假定影像的某一个像元为(i,j),该像元的灰度值为p(i,j),以该像元为中心的邻域为R:R={(m,n)‖m-i≤r,n-j|≤r},r为领域半径。如图 3所示,Lθ为过中心点(i,j)角度为θ的一个方向分界线,Lθ将处理邻域分割为S1和S2两部分,则将像素点(i,j)的方向信息测度定义为
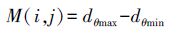 (2)
(2) 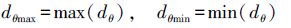 (3)
(3) 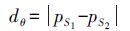 (4)
(4) 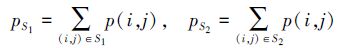 (5)
(5) 边缘纹理点具有方向特性,因此,当Lθ的方向与边缘点的方向一致时,dθ取得最大值。由于边缘两侧像元的灰度值差异较显著,相应的M(i,j)的值也较大,因此方向信息测度有利于提取边缘纹理等细节信息。
|
| 图 3 方向信息测度结构 |
遥感融合方法中,GS、小波变换方法较为突出,GS是利用多光谱波段模拟产生全色波段,并与多光谱波段进行GS变换,采用替代法将变换后的全色波段替换为高分辨率的全色波段,达到融合的效果。小波变换方法则是经小波正变换后获取频域信息,用全色波段的高频分量将多光谱波段的高频分量逐个替换,再进行小波逆变换,即可得到空间分辨率增强的融合影像。本文方法不仅仅是通过简单的替代,而是综合考虑了两幅影像的特征与优势,按照融合规则获取每一频域的系数,最后通过NSCT逆变换重构影像,因此比传统的GS融合算法、小波变换算法更具优势。
基于NSCT的方向信息测度融合方法首先将多光谱影像MS重采样至与全色影像PAN相同空间分辨率,并对影像进行配准;其次将待融合的PAN影像与MS影像进行NSCT正变换,得到PAN、MS影像的低频系数Ljp(x,y)、LjM(x,y),高频系数Hjp(x,y)、HjM(x,y),其中,j为影像的分解尺度;选取一定的融合规则对Ljp(x,y)和LjM(x,y)进行区域灰度方差融合,得到低频融合图像Flow;而对于高频分量则采用改进的方向信息测度对Hjp(x,y)和HjM(x,y)进行融合,得到高频融合图像Fhigh;对Flow和Fhigh进行NSCT逆变换,重构得到最终的融合影像,基于NSCT频域的方向信息测度融合方法基本框架如图 4所示。
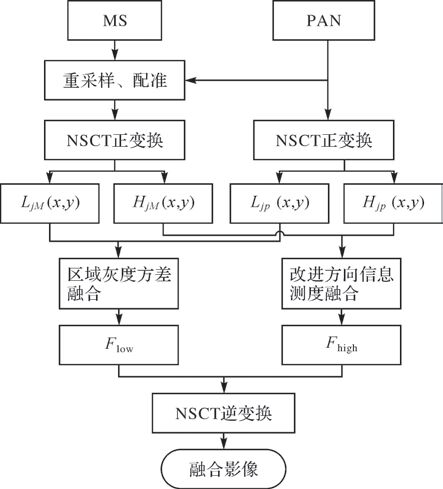
|
| 图 4 影像融合流程 |
低频分量包含大量影像信息,反映了影像的整体轮廓,因此如何选取合适的低频融合系数,将直接决定融合影像的整体质量。低频系数的选择规则一般基于灰度均值、区域熵值等方法进行选择,这种方法仅考虑视觉效果,不仅会降低融合影像的对比度,还会造成部分能量信息损失,并未充分考虑频域的强度变化等包含在内的细节信息,而在影像的低频系数中包含较多的灰度及光谱信息。基于此,本文低频系数的融合采用了基于区域灰度方差的融合规则。区域灰度方差δ2反映了该区域灰度变化的离散程度,δ2值越大表示越离散,区域所包含的灰度越丰富,δ的计算公式为
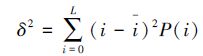 (6)
(6) 式中,i∈[0,L-1];L表示在以(m,n)为中心的M×N窗口范围内的灰度级数,各灰度像素在区域窗口出现的概率为P0、P1、P2、…、PL-1。根据式(6)分别计算出两幅融合影像的各低频系数的区域灰度方差,然后根据以下规则选择融合系数
当δP2(m,n)≠δM2(m,n)时
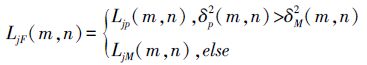 (7)
(7) 当δP2(m,n)=δM2(m,n)时
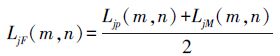 (8)
(8) 高频信号包含了影像的纹理、边缘等细节信息,方向测度信息可以有效地提取边缘纹理信息,然而当影像的噪声水平较高时,噪声处可能会出现方向信息测度较大的情况[10],为此本文采用了灰度和之差的平均值对方向信息测度进行改进。由于噪声处的各方向上灰度和之差的总和较小,有利于区分噪声和纹理边缘信息,像元点(i,j)的各方向灰度和之差dθ的平均值定义为
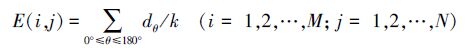 (9)
(9) 式中,M×N为影像处理窗口;k为该窗口的方向信息测度方向数。
将E(i,j)归一化到(0,1)区间
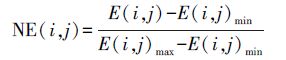 (10)
(10) 改进的方向信息测度为
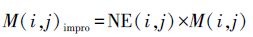 (11)
(11) 本文采用改进的方向信息测度加权融合方法实现高频系数的融合,公式为
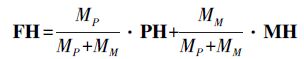 (12)
(12) 式中,FH表示融合影像的高频系数矩阵;PH为全色影像高频系数;MH为多光谱影像高频系数;“·”表示点乘。
三、 试验结果与分析 1. 试验数据与评价标准GF1卫星的投入使用开启了我国高分辨率对地观测的新时代,文中使用的试验遥感影像数据为2014年6月长沙县江背地区的GF1-PMS数据,选取的试验范围轮廓纹理信息较丰富。与现有的国外高分卫星影像(如IKONOS、QuickBird等)相比,GF1幅宽较大,在大范围高分遥感应用研究中具有很大的优势。现有的商业遥感影像处理软件也可对GF1进行融合处理,但其方法仍存在一定的影像细节失真和光谱失真,为此如何提高GF1影像的空间分辨率同时保持其丰富的光谱信息是本文研究的关键。
本文遥感影像融合的算法主要通过Matlab程序实现,如图 5所示,PAN全色影像与MS多光谱影像为输入图像,试验范围为163×168像素,包括水体、道路、耕地、林地、建筑等地物,两幅源影像已经过配准,并将本方法的融合结果与常用的小波融合方法、Gram_Schimdt(GS)变换法的融合结果进行对比分析。影像融合效果通过两个方面进行评价:①通过目视解译对影像进行分析与评价;②通过一定的数理统计参数对影像的能量、纹理、光谱等进行统计分析,即客观定量评价,评价指标包括平均信息熵H、体现空间细节轮廓信息的方差SD、影像清晰度g及表示光谱保真度的光谱扭曲程度D、影像相关系数R,各评价指标统计量见表 1。

|
| 图 5 源多光谱影像 |
| 融合方法 | SD | H | g | D | R |
| 源多光谱影像 | 13.17 | 6.42 | 2.53 | ||
| 源全色影像 | 15.73 | 10.52 | 4.86 | ||
| GS融合算法 | 12.89 | 10.32 | 3.78 | 6.24 | 0.91 |
| 小波变换融合 | 13.24 | 16.52 | 3.99 | 7.52 | 0.89 |
| 本文算法 | 13.96 | 20.45 | 4.28 | 4.82 | 0.93 |
融合结果如图 5—图 9所示,由图中目视解译可以发现3种方法的融合影像空间分辨率比源多光谱影像都有了一定的提高,本文方法与小波变换方法在空间分辨率方面提升效果显著。在空间细节表达能力方面,本文方法和小波变换方法较一致,细节表达明显优于GS融合方法,图像的清晰程度基本能与源全色图像(图 6)保持一致,但小波变换的边缘轮廓信息没有得到很好的保持,如图 9中在耕地、道路轮廓等信息的保持方面显然本文方法表现更佳。

|
| 图 6 源全色影像 |

|
| 图 7 GS融合影像 |

|
| 图 8 小波变换融合影像 |

|
| 图 9 本文算法融合影像 |
从表 1的统计数据分析,本文方法的融合结果各项指标都优于小波变换融合算法、GS融合算法。小波变换算法在方差、信息熵和清晰度等指标都优于GS融合算法,表明小波变换在影像空间细节表达方面较显著,但在光谱保持上却不如GS算法。GS方法尽管其光谱保持能力较强,但细节信息注入不够,导致图像的空间信息失真,视觉效果较差。本文采用基于NSCT变换域的方向信息测度算法,有效地捕捉了源图像的细节信息和边缘信息,平均梯度的提高使得融合图像更加清晰,融合效果更好,光谱扭曲度的降低表明光谱信息的有效保持,本文方法很好地保持了两幅源图像的重要信息,融合结果更接近于标准图像,是一种较理想的图像融合算法。
四、 结束语遥感影像融合的关键在于能够有效反映影像的空间细节信息和光谱信息,根据当前影像融合方法存在的问题,综合了NSCT变换和方向信息测度算法在影像信息表达中的优势,本文提出了一种基于NSCT变换域的方向信息测度融合算法。首先采用NSCT变换方法对目标遥感影像进行多方向多角度分解,分解后的低频系数采用区域灰度方差的融合规则、高频系数采用改进的方向信息测度的融合规则,对GF1影像的多光谱影像与全色波段影像做试验分析,并与常用的小波变换融合算法、Gram_Schimdt融合算法进行对比试验。试验结果显示,本文方法在多光谱波段光谱信息保持中,最接近原始GF1多光谱影像,能够更好地保留源多光谱影像的光谱信息;客观统计评价显示本文方法能够有效地捕捉源图像的细节信息和边缘信息,图像清晰度较高,融合效果更佳,而光谱扭曲度的降低表明光谱信息的有效保持。通过与小波变换融合算法、Gram_Schimdt融合算法的对比试验表明基于NSCT变换和改进方向信息测度结合的融合算法能更好地保持多光谱影像的光谱信息和全色影像的空间细节信息,具有更多的细节特征及更清晰的边缘,提高了遥感影像的解译精度和解译效率,为目标信息的提取和使用提供了技术支持。然而,相对一般算法,本文算法还存在一定的不足,如何提高本文算法对不同影像的适用性及运算速率还需要进一步的探讨与研究。
| [1] | 陶发达, 韩玲, 王惠英, 等. 一种基于HIS融合方法的改进方法[J]. 微计算机信息 , 2011 (11) : 154–156. |
| [2] | 彭实, 张爱武, 李含伦, 等. 一种改进的弱光谱畸变PCA融合方法[J]. 光谱学与光谱分析 , 2013 (10) : 2777–2782. |
| [3] | 邓书斌, 陈秋瑾, 杜会建. ENVI遥感图像处理方法[M]. 北京: 高等教育出版社 ,2014 . |
| [4] | 王慧贤, 江万寿, 雷呈强, 等. 光谱与空间局部相关的SVR影像融合方法[J]. 测绘学报 , 2013, 42 (4) : 508–515. |
| [5] | VETTERLI M. Wavelets, Approximation and Compression[J]. IEEE Signal Processing Magazine , 2001, 18 (5) : 59–73. DOI:10.1109/79.952805 |
| [6] | DO M N, VETTERLI M. Wavelets Beyond[M]. [S.l.]: Academic Press , 2002 . |
| [7] | CUNHA A L, ZHOU Jianping. The Nonsubsampled Contourlet Transform:Theory, Design, and Applications[J]. IEEE Transactions on Image Processing , 2006, 15 (10) : 2091–2106. |
| [8] | YANG H J, LIANG D Q, BI S. Pixel Classification Based on Orientation Information Measure of Image[J]. Journal of Image and Graphics , 2001, 5 (6) : 429–433. |
| [9] | YANG H J, LIANG D Q, BI S. Pixel Classification Based on Orientation Information Measure of Image[J]. Journal of Image and Graphics , 2001, 5 (6) : 429–433. |
| [10] | 杨海军, 梁德群, 毕胜. 基于图像方向性信息测度的图像像素分类[J]. 中国图象图形学报 , 2001, 5 (6) : 429–433. |


