卫星导航观测量的粗差探测修复,尤其是多个粗差的探测修复,是卫星导航接收机完备性监测的研究热点[1-2]。卫星导航中,只有准确获取伪距观测值的精度和偏差信息才能保证定位精度[3]。由于受卫星姿态、空间环境、观测环境及接收机噪声等的影响,伪距观测值难免存在粗差。对伪距粗差进行探测修复是有必要的,而国内外学者的研究对伪距粗差的探测修复关注较少,主要集中在载波相位的周跳探测修复上,逐渐出现了高次差法、电离层残差法、多项式拟合法、多普勒积分法、伪距相位组合法、拟准检定法、小波分析法、卡尔曼滤波法等周跳探测修复方法[4-6]。
较为常见的伪距粗差探测方法有:伪距相位组合法、伪距定位残差判断法。前一种方法不容易区分粗差是源于伪距粗差或载波相位周跳,后一种方法在多颗卫星伪距观测量同时出现粗差时将难以定位[3]。而本文方法是基于历史伪距时间序列的时间相关性和不同卫星伪距间的空间相关性进行伪距粗差的实时探测与修复的。
一、 开窗探测修复法要使得开窗粗差探测修复法奏效,就必须利用窗口内伪距信息精准地定位粗差,再利用窗口内伪距的互相关性进行粗差修复。该方法主要涉及窗口长度设置,伪距的时间相关性、空间相关性探测,粗差修复3方面内容。
1. 时间相关性探测时间相关性探测,即利用窗口内同一卫星的历史伪距时间序列预测当前伪距,并对当前伪距实测值进行合理性检验。利用当前历元k的前l个历元(窗口长度为l)的伪距值拟合预测当前伪距,再获取伪距预测值和实测值的残差,并将伪距残差标准化使其服从标准正态分布,最后进行粗差的时间相关性探测,具体过程为
(1) 多项式拟合预测
采用多项式拟合预测法,假设窗口内伪距集$\bar{\rho }$=$\bar{\rho }$k-l $\bar{\rho }$k-l+1…$\bar{\rho }$k-1,则当前历元伪距预测值$\hat{\rho }$k为
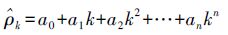 (1)
(1) 式中,a0,a1,a2,…,an为一组多项式系数,由$\bar{\rho }$中的伪距拟合得到,需说明的是$\bar{\rho }$与实测伪距集ρ=ρk-lρk-l+1…ρk-1略有不同,它是经过粗差修复后的伪距;n为多项式最高阶数。
(2) 最高阶数n的确定
n与拟合精度要求有关,认为当窗口内伪距拟合精度Δ小于阈值d时,对应的n即为所求。设窗口内伪距拟合值为$\bar{\rho }$=$\bar{\rho }$k-l$\bar{\rho }$k-l+1…$\bar{\rho }$k-1,令Δ=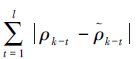
分析表 1可得,阈值越小,阶数越高,拟合精度越高,但拟合时间越长,实际应用中应综合考虑。考虑到伪距的量级较大,其拟合精度在米级即可,因此本文中n取6。
(3) 伪距残差
将伪距实测值与预测值作差,得到伪距残差vk=ρk-$\hat{\rho }$k。
(4) 伪距残差标准化
假设k历元的前l个历元的伪距残差为v=[vk-lvk-l+1…vk-1]。由于观测环境的复杂性,伪距残差往往不服从标准正态分布,现将其标准化,使其服从标准正态分布。k历元伪距残差vk的标准化公式为
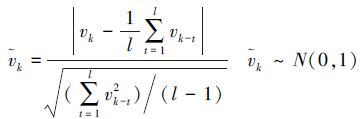 (2)
(2) (5) 时间相关性探测
若当前伪距出现粗差,伪距残差vk必然反常,进而引起标准化伪距残差$\bar{v}$k增大。因此,标准化伪距残差k可作为探测伪距粗差的时间相关因子。
2. 空间相关性探测空间相关性探测即对当前时刻各卫星伪距观测量进行一致性检验。一些外界因素会使得当前所有卫星伪距观测量发生等量跳变,如接收机校时,这种类型的跳变不影响定位,不能判定为粗差,而在发生跳变的历元处,时间相关因子(标准化伪距残差k)必然会增大,若只考虑时间相关因子,则会将该历元的伪距观测量误认为含有粗差。此时,需要空间相关因子来判断所有伪距观测量是否发生等量跳变。
等量跳变一般幅度较大,但由于是跳变时等量的,故各卫星伪距残差的离散程度很小,因此空间相关因子能衡量其离散程度即可。由于不发生跳变与发生跳变时各伪距残差的均值不同,对于均值时变序列的离散程度,用标准差来衡量显得不合理,变异系数是标准差与均值的比值,常用来衡量均值时变序列的离散程度,故本文以当前各伪距残差的变异系数作为空间相关因子ck,即
 (3)
(3) 式中,vki为k历元卫星i的伪距残差;m为k历元可视卫星数量。
当所有卫星伪距观测量发生等量跳变时,虽然时间相关因子$\bar{v}$k急剧变大,但空间相关因子ck基本不受影响,甚至变小。
3. 时间与空间相关性探测的融合伪距粗差探测应综合考虑伪距时间相关性和空间相关性,故时间相关性探测和空间相关性探测的融合是关键之一,融合原则是:当由时间相关性探测到粗差时,若由空间相关性未探测到粗差,则认为伪距发生等量跳变,若由空间相关性也探测到粗差,则认为存在粗差;当由时间相关性未探测到粗差时,则不考虑空间相关性探测,认为未探测到粗差。根据该融合原则建立探测伪距粗差的膨胀因子w,即
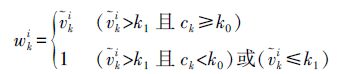 (4)
(4) 式中,wki为k历元卫星i的膨胀因子;k0为空间相关因子ck判定有粗差的阈值;k1为时间相关因子k判定有粗差的阈值。膨胀因子wki为1则说明不存在粗差,否则其值越大则说明存在粗差的可能性越大。
(1) k0的确定
考虑到空间相关因子为变异系数,是标准差与均值的比,其值不超过k0则认为当前数据稳定合格,这在工业制造、医学等行业也有广泛应用。在白细胞过氧化物传感器研制中,制备固定细胞膜的重现性变异系数为5.5%[7];在《实验室质量控制规范》(GBT 27404—2008)中,根据成分浓度的不同其变异系数阈值变动在1.3%~43%。另外,当所有卫星伪距出现等量跳变时其变异系数往往较小,理论上应将k0设小一点以便能更好地识别等量跳变。因此根据实际情况和变异系数的数学性质,本文k0设为0.1。
(2) k1的确定
k1值应根据观测量的特点进行选取,通常选2.5~8.0。对于大地测量,因有较强的几何检核,选3.0左右合适;对于卫星激光测距和卫星伪距观测值,选8.5左右为宜[8]。综合考虑,本文k1设为8。
4. 粗差修复定位粗差后,需要修复粗差。修复粗差是为了减小当前粗差对后续历元伪距预测及粗差探测的影响,且面对连续粗差仍可稳健定位,当可视星少于4颗时也可直接用修复后伪距进行定位解算。粗差修复策略应充分考虑粗差的类型,本文从突变型粗差、连续型粗差着手,充分考虑多星同时且连续出现粗差等复杂情景,提出一种窗口内观测相关修复法。
窗口内观测相关性修复法,即认为窗口内的观测量是相关的,并且离当前历元越近的历元,其观测量与当前观测量相关性越强。基于该观点,详细叙述本文修复策略。
(1) k历元(即标杆历元K)伪距修复
当k历元卫星i的伪距膨胀因子wki超过阈值k1(此时历元作为标杆历元K,伪距残差作为标杆残差V),认为伪距观测量存在粗差,将其伪距预测量$\hat{\rho }$k作为修复后伪距$\bar{\rho }$k,即
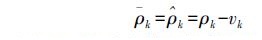 (5)
(5) (2) K+Δk历元伪距修复(Δk<l)
伪距修复过程只修复伪距,不修复对应的伪距残差,故k+Δk历元的伪距预测不受k历元粗差影响,而其伪距残差标准化过程将受到一定影响导致膨胀因子不够准确。不修复伪距残差的原因为:一是修复方法匮乏;二是若修复不恰当,会扰乱窗口内伪距残差的分布,严重影响其标准化,从而引起不可预知的后果。考虑K+Δk历元的膨胀因子不够准确,并且伪距预测不受粗差影响,其伪距残差较好地反映了伪距质量,为避免粗差漏检,故将K+Δk历元的粗差判定条件宽松为:膨胀因子超过阈值k1(进行标杆更新)或伪距残差大于$\bar{v}$的一半,即
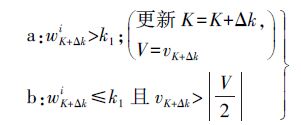 (6)
(6) 当K+Δk历元满足式(6)中的条件a时,按式(5)修复伪距;满足条件b时,考虑窗口内观测相关性,按式(7)修复伪距。
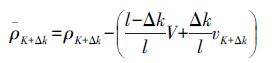 (7)
(7) 式中,ρK+Δk为K+Δk历元的伪距观测量;vK+Δk为历元K+Δk的伪距残差。从式(7)中可看出,Δk越大,K+Δk历元的伪距修复与K历元相关性越弱。
(3) K+Δk历元伪距修复(Δk≥l)
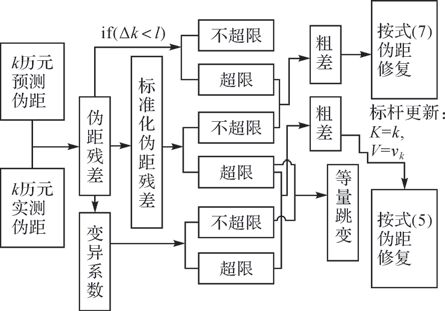
当Δk≥l时,则继续按步骤(1)、(2)修复伪距。流程归纳如图 1所示。
|
| 图 1 开窗探测修复流程 |
为分析本文修复方法的特点,现与两种传统修复方法作比较:一是当出现粗差时,直接以伪距预测量作为修复值;二是以伪距预测量和观测量的均值作为修复值。分别在81、101~105 s的北斗1号星伪距观测量上加入10 m的粗差,在3种修复方法下,修复后伪距与参考伪距的差值见表 2。
| m | ||||||
| 方法 | 历元/s | |||||
| 81 | 101 | 102 | 103 | 104 | 105 | |
| 传统法1 | 0.3 | 0.4 | 1.3 | 3.1 | 10.0 | 20.0 |
| 传统法2 | 0.3 | 0.4 | 5.6 | 3.1 | 10.0 | 15.0 |
| 本文方法 | 0.3 | 0.4 | 0.4 | 0.5 | 0.5 | 0.5 |
从表 2可看出,传统法在出现突变型粗差时的修复效果和本文方法相同,但在出现连续型粗差时效果远不如本文方法。因此,本文修复法的性能较优。
二、 窗口确定关于伪距时间序列的窗口长度l的选取往往是个难题,近几年来受到了学者关注,实践中通常设为经验值[9-10]。窗口长度过长,需存储大量历史伪距信息,且太旧的伪距信息对当前伪距预测的作用不大,而且其误差反而会影响当前预测;但窗口长度过短,窗口内伪距的误差对当前预测的影响无疑增大了。因此,窗口长度理论上存在最优值。
本文是用窗口内的伪距拟合预测当前伪距,另一种预测方法是用窗口内伪距和当前伪距观测量一同预测得到当前伪距最终预测$\hat{\rho }$k,称为平滑法,即
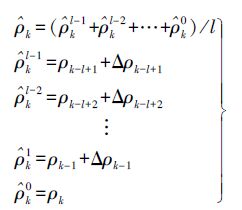 (8)
(8) 式中,$\hat{\rho }$kl-1,…,$\hat{\rho }$k0分别是窗口内伪距观测量ρk-l+1,…,ρk对当前伪距的预测值;Δρk-l+1,…,Δρk-1则是相应的伪距增量。当前伪距最终预测k为窗口内各伪距对当前伪距预测值的均值。
平滑法中,假设当前伪距真值为$\bar{\rho }$k,则有
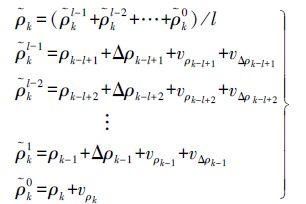 (9)
(9) 式中,窗口内各伪距对当前伪距预测值包含两类误差:一是伪距观测误差vρ,二是伪距增量误差vΔρ。平滑法中也存在类似本文拟合预测的窗口选择问题,窗口过长,存储量大,伪距增量误差增大;窗口过小,难以平滑准确。当伪距增量误差未积累到一个不可忽略的影响时,窗口越长越好,故在理论上,其窗口也存在最优值。
平滑法中,窗口内的伪距与当前伪距的关联性越强,其在平滑过程中的重要性越大,最优窗口就是要判断一个截点,刚好使得截点之外的历史伪距与当前伪距基本不相关;本文对当前伪距的预测过程中,也是需要判断这么一个截点,刚好使得截点之前的伪距对预测过程作用甚微,可有可无。因此,可近似地将本文拟合预测的最优窗口与平滑法的最优窗口等同。
现求取平滑法的最优窗口。由式(8)和式(9)可得,当前伪距最终预测的误差ε为
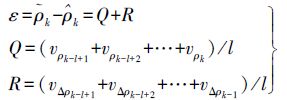 (10)
(10) 则当前伪距最终预测误差ε的均方根误差平方值为
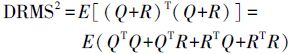 (11)
(11) 为求取窗口l的最优值,将DRMS2对窗口l求导后令其等于零,解出的窗口l为最优值。假设式(9)中的伪距增量由当前载波相位与历史载波相位相减求得,以k-l+1历元为例,伪距增量Δρk-l+1=φk-φk-l+1,则伪距增量误差vΔρk-l+1近似等于两历元载波的载波噪声差和相应的电离层延迟变化量,而对流层延迟等误差被消去了。由于载波与伪距受电离层延迟的影响具有大小相等,符号相反的特点,因此vΔρk-l+1包含的电离层延迟变化量是两历元间电离层延迟变化量的2倍,即vΔρk-l+1=(vφk-vφk-l+1)-2(l-1)idot,则
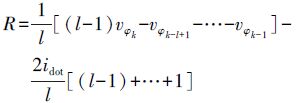 (12)
(12) 式中,vφ是载波噪声;idot为1 s的电离层延迟变化量,近似为不变量。由于载波噪声远小于伪距噪声,可忽略不计,只考虑电离层延迟变化量,则
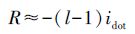 (13)
(13) 假设伪距噪声vρ ~N(0,σρ2),则E(Q)=0,E(QTQ)=$\frac{1}{l}$σρ2。则式(11)变为
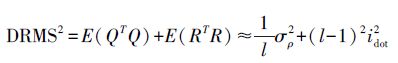 (14)
(14)
前已叙及,当
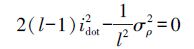 (15)
(15) 经查阅资料,idot2约为0.013 6 m,σρ取2 m[11],代入式(15)中求得l最接近整数23,因此窗口最优值为23。故本文取窗口长度l为23 s。
三、 试验分析为了验证本文方法处理多类型粗差和等量跳变的能力,设计两次试验。
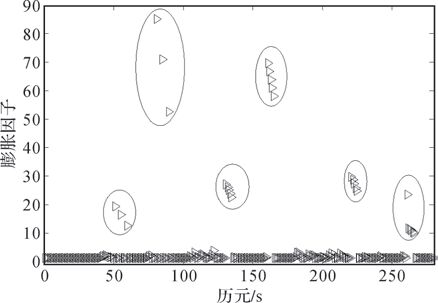
1) 试验1:一种良好的粗差探测修复方法往往能适应多种类型的粗差。为验证开窗探测修复法的性能,分别在伪距原始观测量中加入突变小粗差、突变大粗差、等量连续小粗差、等量连续大粗差、缓变连续小粗差、缓变连续大粗差等多种类型粗差。试验数据为2016年5月4日用GNSS信号源模拟动态跑车数据,频点为北斗B3频点,时长3837 s,采样间隔1 s。分别在1号星伪距原始观测量的前后27处加入不同类型的粗差,经过本文探测修复方法作用后,粗差探测情况参考膨胀因子,如图 2所示,修复情况如图 3所示。
|
| 图 2 1号卫星膨胀因子 |
|
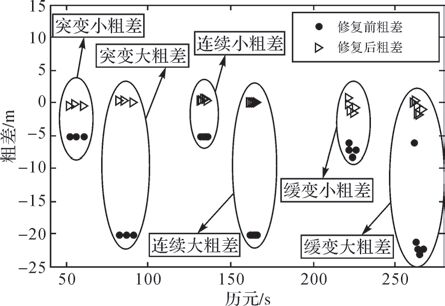
| 图 3 粗差修复效果 |
从图 2可看出,提出的开窗探测修复方法能有效探测多种类型误差;从图 3可看出,该方法对突变型和连续型粗差的修复能力最强,对缓变型粗差修复能力稍差,但也能较好地剔除粗差。
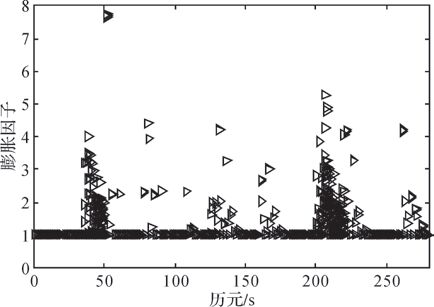
2) 试验2:根据GNSS伪距特点,同一历元所有卫星伪距发生等量跳变时,不影响定位,因此这种跳变不应作为粗差。传统的探测修复方法会将其作为粗差处理,而本文开窗探测修复法能准确识别这种跳变,现以试验说明。试验数据、加入伪距跳变的历元都与试验1相同,只是在这些历元的所有可视卫星伪距原始观测量上加入100 m等量跳变。经本文方法处理后,所有可视卫星的膨胀因子如图 4所示。
|
| 图 4 所有卫星膨胀因子 |
从图 4可看出,虽然在部分历元的所有可视卫星伪距观测中加入了100 m的等量跳变(不影响定位),但利用本文方法求出的所有卫星的膨胀因子均未超过阈值k1(k1为8),从而不将这类跳变视为粗差,这是合理的。因此本文方法能正确处理这类跳变。
四、 结束语针对GNSS伪距的特性,本文提出了一种基于同一卫星历史伪距时间序列的时间相关性、不同卫星伪距间的空间相关性的开窗探测修复方法。试验证明,该方法能有效探测及修复突变型、连续型、缓变型等伪距粗差,并能合理处理由接收机校时等原因引起的所有可视卫星伪距的等量跳变现象。
| [1] | 吴云. GNSS粗差检测的"快照"法与"滤波"法的比较研究[J]. 武汉大学学报(信息科学版) , 2010, 35 (6) : 649–652. |
| [2] | 沙海, 黄新明, 刘文祥, 等. 基于非相干积累的微小伪距偏差RAIM方法研究[J]. 宇航学报 , 2014, 35 (6) : 708–712. |
| [3] | 王甫红, 刘基余. 星载GPS伪距测量数据质量分析[J]. 测绘科学技术学报 , 2007, 24 (2) : 97–99. |
| [4] | 李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报 , 2011, 40 (6) : 718–729. |
| [5] | 龚学文, 王甫红. 低轨卫星星载GPS数据伪距粗差及相位周跳探测与分析[J]. 测绘通报 , 2016 (2) : 17–21. |
| [6] | 刘文祥, 李峥嵘, 王飞雪. 一种可检测和改正微小慢变伪距偏差的新RAIM方法[J]. 宇航学报 , 2010, 31 (4) : 1024–1029. |
| [7] | 那晓琳, 张宏绪. 白细胞过氧化物传感器的研制[J]. 传感技术学报 , 1995, 8 (2) : 39–43. |
| [8] | 杨元喜. 自适应抗差最小二乘[J]. 测绘学报 , 1996, 25 (3) : 206–211. |
| [9] | 杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版) , 2003, 28 (6) : 714–718. |
| [10] | GUO J F, OU J K, YUAN Y B. Optimal Carrier-smoothed-code Algorithm for Dual-frequency GPS Data[J]. Natural Science , 2008 (18) : 591–594. |
| [11] | 尚书亮, 李锐, 黄智刚. 利用卡尔曼滤波估计导航信号电离层差分改正[J]. 武汉大学学报(信息科学版) , 2010, 35 (9) : 1021–1023. |


