随着我国工程建设的需要,钢板桩围堰由于其水密性好、施工简便、节约空间、可重复利用及环保等优点,在国内大型基坑工程和涉水工程中的应用越来越广泛。但钢板桩围堰安全易受地质条件、施工工况、水位、天气等各种复杂因素影响,极易成为工程安全的不稳定因素。国内对钢板桩围堰安全的研究多是从其设计结构特点出发来进行数值模拟分析的[1-2],对钢板桩围堰的变形监测研究较少,尚未构成系统。武汉东湖隧道工程作为武汉市重点工程,是为缓解武汉城市交通压力,在国内最大城中湖--武汉东湖湖底规划设计的一条湖底隧道。本文结合东湖湖底隧道工程中大跨度钢板桩围堰的实测形变数据,分析其形变特点,探索出与其适应的预测模型,从形变预测的角度研究钢板桩围堰的安全性和稳定性。
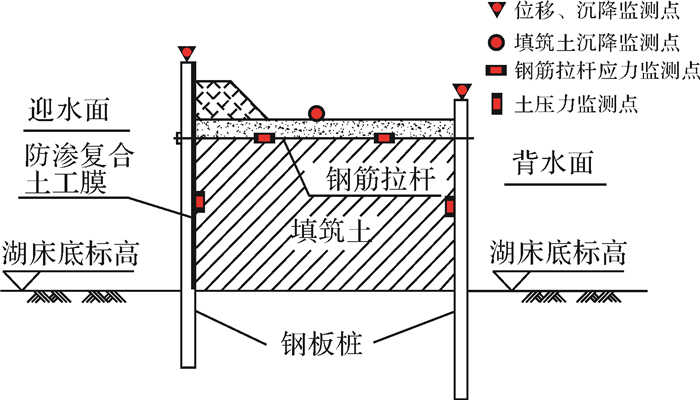
一、 大跨度钢板桩围堰的特点东湖隧道是目前国内最长的城中湖底隧道,全长10.6 km,采用明挖顺作法施工,湖中段约7 km的主体结构在施工前构筑了拉森Ⅳ型双排钢板桩围堰,形成施工场地,其横断面结构如图 1所示。钢板桩围堰呈带状分布在线路两侧,具有大跨度的特点。围堰变形体主要监测内容包括钢板桩顶部水平位移及沉降、钢筋拉杆应力、填筑土压力及沉降。本文选取能直接反映围堰形变的围堰顶部垂直钢板桩的横向水平位移作为围堰变形的分析变量。
|
| 图 1 钢板桩围堰横断面示意图 |
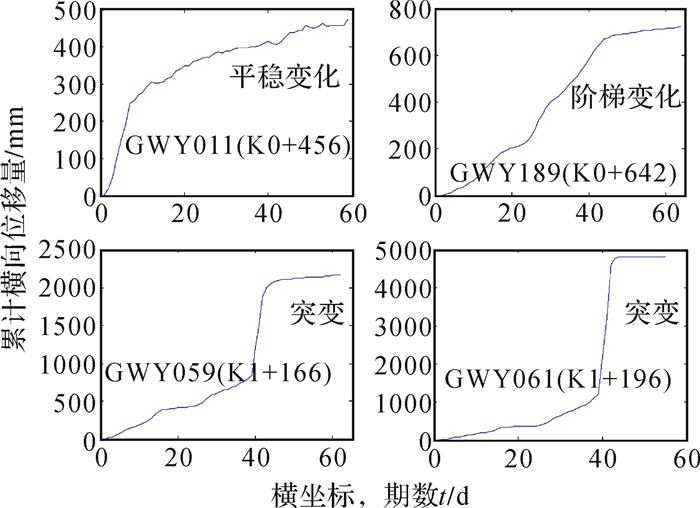
通过对东湖隧道工程K0+300-K2+720段264个钢板桩位移监测点变形数据的分析可知,从整体上大跨度钢板桩围堰形变呈现出大量级、强趋势、波动性的特点;变形具有明显的三维空间效应,围堰中段位移量明显大于两端,围堰迎水面钢板桩位移量大于背水面;围堰位移量受施工工况影响较大,特别是在围堰抽水期尤为明显。从每个特征点的变形曲线分析,本文将大跨度钢板桩围堰的变形特征分为平稳变化类、阶梯变化类和突变类,如图 2所示。对于数据预报,更加关注的是近几期数据的变化速率,根据规范及专家意见,东湖隧道钢板桩变形三级预警值定为连续3天变化速率大于20 mm/d,本文将大跨度钢板桩围堰的变形预报问题分为低增长序列(0~20 mm/d)预测和高增长序列(20~40 mm/d)预测问题。
|
| 图 2 钢板桩形变数据变化类型 |
预测理论方法多种多样,从变形体的变形机理角度分析:有认为形变数据之间存在内在联系和规律的回归分析、时序分析方法;有认为变形数据没有规律性,将数据作相应处理后让数据呈现出相应规律的灰色理论方法;有认为形变值与各相关因素之间存在高度非线性关系,通过挖掘这种关系,来反映变形体复杂变形内在特征的神经网络理论、数据组合分组(GMDH)理论方法;还有马尔科夫模型、小波分析模型、卡尔曼滤波模型等。此外,还有吸收各单项模型优势的权系数组合、非线性组合和自组织组合类型的组合模型。
本文从变形体的形变特征角度出发,针对大跨度钢板桩围堰大量级、强趋势和波动性的数据特点,分析了时序分析理论、灰色理论和自组织数据挖掘理论方法对大跨度钢板桩围堰形变预测的适应性。时序分析理论采用一种无需对建模时间序列平稳化处理,适用于趋势预测和实际工程的DDS建模方法[3]。针对GM (1, 1)对高增长序列预测有滞后效应和不适合中长期预测的弊端,对模型的背景值构造[4]、参数计算方法[5]和建模初始值选择[6]进行改进,建立了改进的动态等L维新息灰数递补GM (1, 1)模型。针对数据波动性的特点,采用一种有效的非线性系统辨识方法--数据组合处理方法(GMDH)[7-8],同时考虑计算量及本文数据波动性强弱的特点,设置迭代层数c≤3的迭代终止阈值。最终,利用3种适合不同数据特点的单项预测模型的拟合预测值,以自组织数据挖掘思想为基础构建GMDH组合预测模型。
2. 形变数据预报分析本文选取发生险情后GWY011(K0+456)点的低增长序列和发生险情之前GWY059(K1+166)点的高增长序列数据作为研究对象,具体分析大跨度钢板桩围堰的高、低增长序列预测问题。
(1)低增长序列预测
GWY011(K0+456)点在第6期出现钢筋拉杆断裂的险情,最大位移速率达56 mm/d,通过打设抗滑桩和焊接加固,后期平均变化速率约8 mm/d,变化较平稳,对低增长序列预测问题具有很好的代表性和研究价值。选取该点处于稳定状态前39天的数据,该时段共监测55次,以一天为周期,共获得39期数据,其中第19期数据采用三次样条插值获得,前30期用于建模,后9期用于低增长序列预测检验。
1)通过Matlab编写的软件,获得GWY011点最优时间序列模型为ARMA (2, 1),模型表达式为
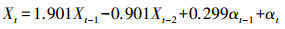 (1)
(1) 2)对于GM (1, 1)模型,利用所编写的软件,获得适合低增长序列的建模步长L=5(见表 1)。
| (%) | ||
| 步长L | 拟合MAPE | 预测MAPE |
| 3 | 5.44 | 9.25 |
| 4 | 5.85 | 1.33 |
| 5 | 7.26 | 0.73 |
| 6 | 8.96 | 1.99 |
| 7 | 10.73 | 2.45 |
| 8 | 13.45 | 2.58 |
获得模型参数a=-0.005 1,u=379.007 7,背景值公式中n=4,初始值中m=4,表达式为
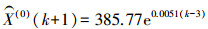 (2)
(2) 然后利用等维灰数递补算得后9期的预测值。
3)单变量时间序列GMDH建模的关键是确定因变量个数m和训练集矩阵比值k。利用软件以预测MAPE (平均绝对百分比误差)最小为原则,获得最优模型(m=7、k=1/2、c=2),结果见表 2。
| (%) | |||||||||||
| m | k | ||||||||||
| 1/3 | 1/2 | 2/3 | 3/4 | ||||||||
| mp | kmp | mp | kmp | mp | kmp | mp | kmp | ||||
| 4 | 5.13 | 17.72 | 2.71 | 14.69 | 1.30 | 1.27 | 1.38 | 2.38 | |||
| 5 | 4.82 | 17.30 | 1.08 | 3.05 | 0.68 | 1.10 | - | - | |||
| 6 | - | - | 1.11 | 10.35 | 0.71 | 2.32 | - | - | |||
| 7 | - | - | 0.62 | 0.81 | 1.16 | 1.42 | - | - | |||
| 8 | - | - | 0.66 | 1.42 | 0.73 | 0.80 | - | - | |||
| 注:mp%为拟合MAPE, kmp%为预测MAPE, “-”表示模型无解。 | |||||||||||
4)将DDS、GM (1, 1)和单变量时间序列GMDH模型的拟合预测值,作为GMDH组合模型的输入值,并利用软件以预测MAPE最小为原则,获得最优组合模型的训练集比k=1/2,迭代层数c=1(见表 3)。
| (%) | ||
| 训练集比k | 拟合MAPE | 预测MAPE |
| 1/3 | 1.24 | 1.31 |
| 1/2 | 1.43 | 0.53 |
| 2/3 | 1.25 | 0.55 |
| 3/4 | 0.76 | 0.88 |
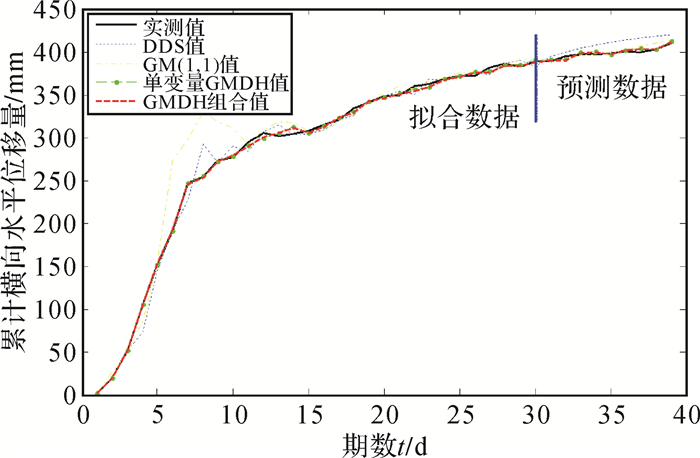
根据以上确定的模型,最终获得各模型向前9期数据的预测值如表 4、图 3、图 4所示。
| 期数t | 实测值/mm | DDS值/mm | GM值/mm | 单变量GMDH/mm | GMDH组合值/mm | 对应建模方法的残差/mm | |||
| 31 | 388.3 | 394.5 | 389.8 | 391.6 | 390.4 | -6.2 | -1.5 | -3.3 | -2.0 |
| 32 | 394.8 | 399.8 | 391.6 | 391.0 | 390.4 | -5.0 | 3.2 | 3.8 | 4.4 |
| 33 | 397.2 | 404.4 | 395.3 | 399.5 | 398.3 | -7.2 | 1.9 | -2.3 | -1.1 |
| 34 | 397.4 | 408.2 | 397.2 | 400.5 | 399.6 | -10.9 | 0.2 | -3.2 | -2.2 |
| 35 | 398.7 | 411.5 | 400.3 | 396.9 | 396.6 | -12.8 | -1.6 | 1.8 | 2.1 |
| 36 | 400.3 | 414.2 | 403.5 | 402.3 | 401.7 | -13.9 | -3.2 | -2.0 | -1.5 |
| 37 | 399.8 | 416.3 | 406.4 | 403.9 | 403.3 | -16.5 | -6.5 | -4.0 | -3.5 |
| 38 | 403.5 | 418.1 | 409.9 | 403.0 | 402.7 | -14.6 | -6.4 | 0.5 | 0.9 |
| 39 | 409.9 | 419.4 | 413.5 | 412.1 | 411.0 | -9.5 | -3.6 | -2.3 | -1.1 |
| MAPE/(%) | 2.51 | 0.73 | 0.80 | 0.53 | |||||
|
| 图 3 GWY011各类预测模型预测值对比曲线 |
|
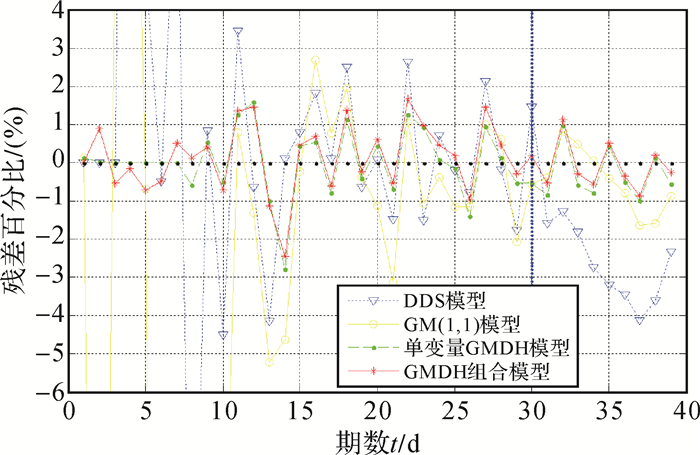
| 图 4 GWY011各类模型预测残差百分比 |
(2)高增长序列预测
GWY059(K1+166)位于围堰二中段,地质条件差,受施工、水位等因素影响,呈现波动性变化,变化速率较大,在第38期出现险情发生突变,当天横向位移量达到708.9 mm,突变前5天内变形速率为20~40 mm/d。选取监测开始到突变前段的监测数据用于建模分析高增长序列预测问题,该时段共监测66次,每天至少监测了一次,仍以一天为周期,数据预处理后获得共37期实测数据,前32期用于建模,突变前5期数据用于高增长序列预测检验。
限于篇幅,具体过程不再详述,同理获得GWY059点DDS法的最终模型为ARMA (2, 1),其表达式为
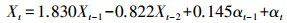 (3)
(3) 改进的GM (1, 1)模型用于向前预测5期数据的模型参数a=-0.029 6,u=606.796 2,背景值公式中n=5,初始值中m=3,表达式为
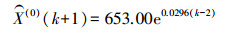 (4)
(4) 单变量时间序列GMDH建模的最优参数因变量个数m=3,训练集矩阵比值k=4/5;GMDH组合模型的训练集比k=3/4。
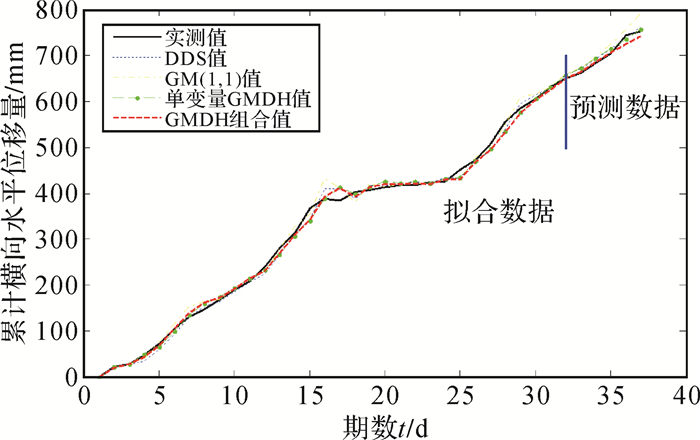
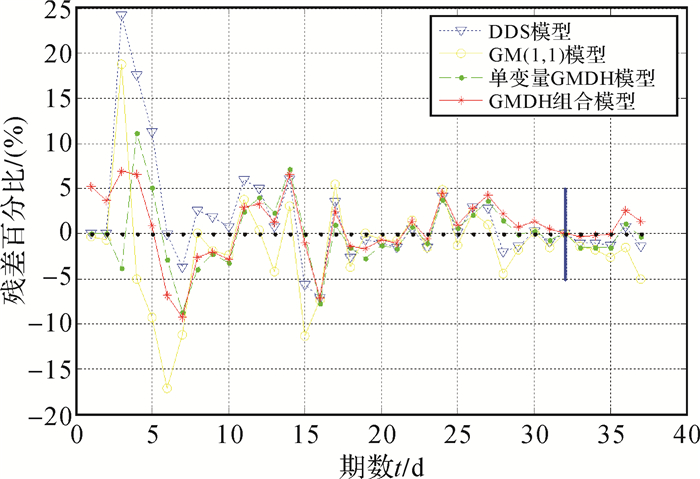
根据以上确定的模型,得到各模型GWY059点向前5期数据的预测值如表 5、图 5、图 6所示。
| 期数t | 实测值/mm | DDS值/mm | GM值/mm | 单变量GMDH/mm | GMDH组合值/mm | 对应方法残差百分比/(%) | |||
| 33 | 663.4 | 670.7 | 672.6 | 673.6 | 665.4 | -1.1 | -1.4 | -1.5 | -0.3 |
| 34 | 684.4 | 691.9 | 697.0 | 694.8 | 686.0 | -1.1 | -1.8 | -1.5 | -0.2 |
| 35 | 705.6 | 714.6 | 724.9 | 716.1 | 706.5 | -1.3 | -2.7 | -1.5 | -0.1 |
| 36 | 744.7 | 738.7 | 756.2 | 736.7 | 725.8 | 0.8 | -1.6 | 1.1 | 2.5 |
| 37 | 753.3 | 764.2 | 791.7 | 756.6 | 743.4 | -1.4 | -5.1 | -0.4 | 1.3 |
| MAPE/(%) | 1.14 | 2.52 | 1.21 | 0.90 | |||||
|
| 图 5 GWY059各类预测模型预测值对比曲线 |
|
| 图 6 GWY059各类模型预测残差百分比 |
为反映各预测模型对预测问题效果的质量,本文采用MAPE (平均绝对百分比误差)、MAE (平均绝对误差)、MSPE (均方百分比误差)、MSE (均方误差)和SSE (误差平方和)指标综合评定模型的精准度,各模型的误差指标值见表 6。
| 方法 | MAPE/(%) | MAE/mm | MSPE/(%) | MSE/mm | SSE | MAPE/(%) | MAE/mm | MSPE/(%) | MSE/mm | SSE |
| GWY011前30期拟合误差指标 | GWY011后9期预测误差指标 | |||||||||
| DDS法GM (1,1)法单变量GMDH GMDH组合 | 3.05 | 7.62 | 1.34 | 2.28 | 3785 | 2.51 | 10.73 | 0.95 | 3.79 | 1165 |
| 7.26 | 14.66 | 2.57 | 4.85 | 19817 | 0.73 | 3.12 | 0.31 | 1.25 | 126 | |
| 0.81 | 2.66 | 0.21 | 0.67 | 240 | 0.80 | 2.58 | 0.23 | 0.93 | 70 | |
| 0.76 | 2.29 | 0.17 | 0.55 | 253 | 0.53 | 2.09 | 0.20 | 0.79 | 51 | |
| GWY059前32期拟合误差指标 | GW059后5期预测误差指标 | |||||||||
| DDS法GM (1,1)法单变量GMDH GMDH组合 | 3.72 | 10.37 | 1.33 | 2.38 | 4128 | 1.14 | 8.12 | 0.52 | 3.70 | 41 |
| 4.00 | 11.27 | 1.21 | 2.79 | 6530 | 2.52 | 18.18 | 1.28 | 9.42 | 91 | |
| 2.75 | 8.87 | 0.81 | 2.16 | 3412 | 1.21 | 8.47 | 0.57 | 3.98 | 42 | |
| 2.97 | 8.77 | 0.75 | 2.07 | 3590 | 0.90 | 6.67 | 0.58 | 4.31 | 33 | |
从文中图表数据及各模型误差指标可以得出:
1) DDS模型对变化转折点的辨识效果不强,但随着数据的变化,能迅速作出调整,能较好预测出数据的变化趋势,高增序列预测MAPE值仅为1.14%,低增长序列的拟合预测MAPE值均在3%左右。
2)改进后的GM (1, 1)模型对高增长序列预测有一定的适应性;对低增长序列预测GM (1, 1)具有明显的优势,预测MAPE仅有0.73%,但随着预测步数的增长,仍然呈现出发散状态。
3)对于单变量时间序列GMDH,发挥了其强大的非线性辨识功能,无论是拟合还是预测的误差,都大大降低。同时,GMDH组合模型进一步提高了预测的精准度,各误差指标明显优于各单项模型。但随着步数的增长,不易预测出变形数据的非线性特性。
4)大量数据验证,对于高增长序列,GM (1, 1)模型步长L取3~5为宜,增长速率与步长L呈负相关;单变量时间序列GMDH中参数k取3/4~4/5,m取3~7为宜;GMDH组合模型m=3确定时,k取2/3~4/5为宜。对于低增长序列,GM (1, 1)模型步长L取4~6为宜;单变量时间序列GMDH中参数k取1/2~2/3,m取5~8为宜;GMDH组合模型m=3确定时,k取1/2~3/4为宜。
综上所述,各预测模型的适应性,对于高增长序列预测问题,GMDH组合>单变量时间序列GMDH>DDS模型>改进GM (1, 1);对于低增长序列预测问题,GMDH组合>改进GM (1, 1)>单变量时间序列GMDH>DDS模型。
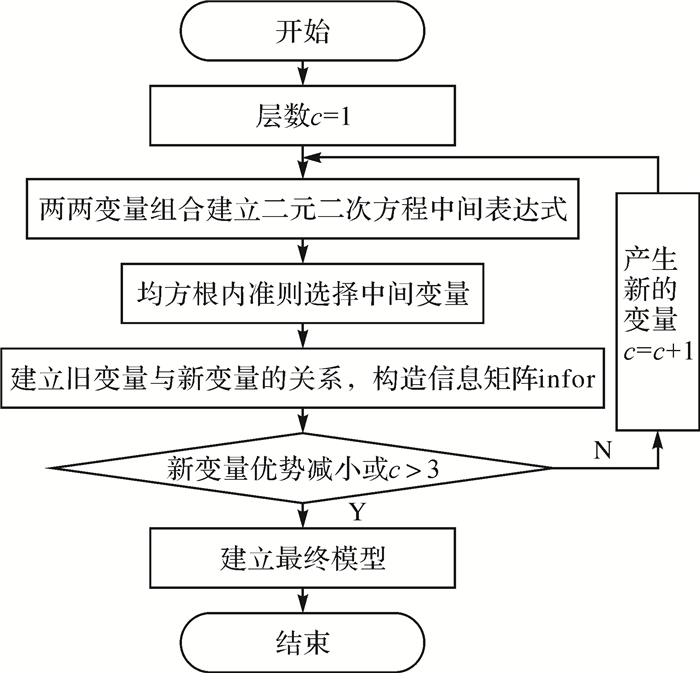
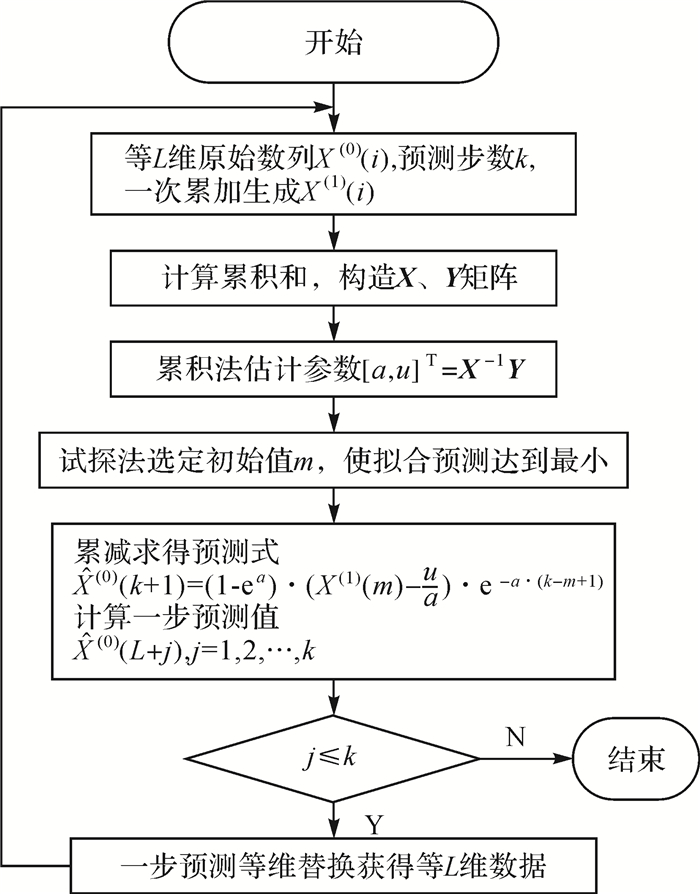
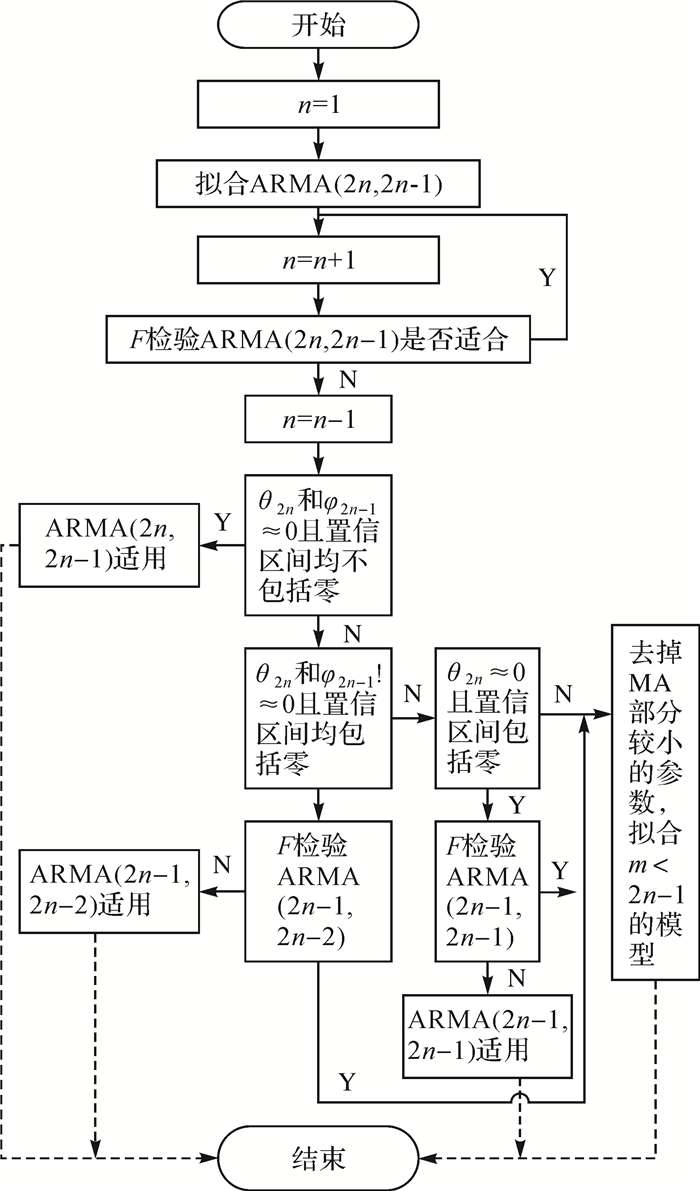
三、 预测软件实现预测软件研制的目的主要是为了提供一个友好的人机交互界面,将预测理论模型实际应用到工程变形监测中,以方便快捷地进行数据的分析与预报。实现软件的关键是模型中的核心算法,各模型算法的流程设计如图 7-图 9所示。
|
| 图 7 GMDH算法流程设计 |
|
| 图 8 改进的GM (1, 1)模型算法设计 |
|
| 图 9 DDS模型算法流程 |
信息矩阵infor记录的是变量组合成部分表达式的整个过程信息,采用Matlab中的“单元阵列”数据结构表示,每一个元素都为一个m×11矩阵,代表一层中所选出新变量的过程信息。
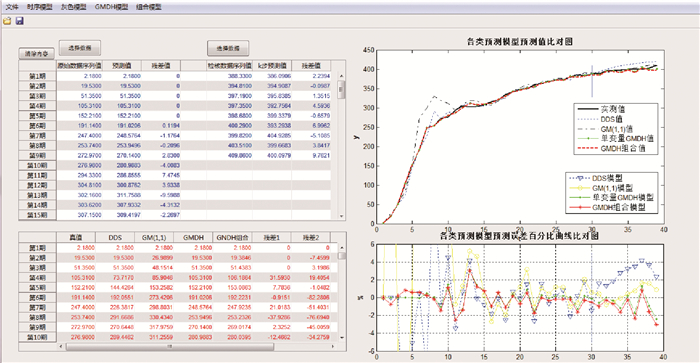
利用Matlab的数据分析与可视化功能[9-10],实现了本文所采用的预测模型方法,以预测平均绝对百分比误差MAPE最小为准则,可快速直观地获得最优预测模型的预测曲线图与预测残差图,如图 10所示。
|
| 图 10 软件界面 |
本文结合武汉东湖隧道工程中大跨度钢板桩围堰实测位移变形数据,对大跨度钢板桩围堰数据的形变特点与预报进行了研究,得出以下结论:
1)大跨度钢板桩围堰变形具有明显的三维空间效应,数据呈现出大量级、强趋势和波动性的特点。
2)针对数据大量级、强趋势和波动性特点,采用DDS模型、改进的GM (1, 1)、单变量时间序列GMDH和新组合形式的GMDH组合模型,并具体分析各模型对高低增长序列预测的适应性及各模型中关键参数的取值范围。
3)采用Matlab实现模型的关键算法,开发了能方便快捷、动态地进行形变数据分析与预报的软件,后期可逐步加入其他实用预测模型,完善软件的功能,扩宽软件的应用范围。
实践验证,本文所建立的单项模型、组合模型形式及编写的预测软件对大跨度钢板桩围堰的形变预测具有良好的效果,为提前了解大跨度钢板桩围堰的变形情况提供了有效途径,对指导施工及变形监测工作具有一定的实际参考意义。
| [1] | 潘泓, 王加利, 曹洪, 等. 钢板桩围堰在不同施工工序下的变形及内力特性研究[J]. 岩石力学与工程学报 , 2013, 32 (11) : 2316–2324. |
| [2] | 张玉成, 杨光华, 姜燕, 等. 软土地区双排钢板桩围堰支护结构的应用及探讨[J]. 岩土工程学报 , 2012, 34 (S1) : 659–665. |
| [3] | 尹晖. 时空变形分析与预报的理论和方法[M]. 北京: 测绘出版社 ,2002 : 23 -37. |
| [4] | 谭冠军. GM (1, 1)模型的背景值构造方法和应用(Ⅱ)[J]. 系统工程理论与实践 , 2000 (5) : 125–127. |
| [5] | 曾祥艳, 肖新平. 累积法GM (1, 1)模型的改进与应用[J]. 统计与决策 , 2009 (5) : 32–35. |
| [6] | 张大海, 江世芳, 史开泉. 灰色预测公式的理论缺陷及改进[J]. 系统工程理论与实践 , 2002 (8) : 140–142. |
| [7] | 张启人, 陈玉宏. GMDH非线性大系统的测辨和预测[J]. 系统工程 , 1984 (1) : 73–82. |
| [8] | 周敏, 李世玲, 张富堂. 数据组合处理方法在数据预测中的应用[J]. 计算机测量与控制 , 2006 (7) : 939–941. |
| [9] | 聂桂根. MATLAB在测量数据处理中的应用[J]. 测绘通报 , 2001 (2) : 39–40. |
| [10] | 薛毅. 实用数据分析与MATLAB软件[M]. 北京: 北京工业大学出版社 ,2015 . |


