地面用户被动接收来自太空的北斗卫星信号,不可避免地会受到人为或自然物的遮挡,造成区域内可接收的卫星数量有限,且卫星分布的几何构型不佳,影响北斗定位的精度、完好性和可用性[1]。此外,受卫星导航系统本身结构所限,其垂直方向的定位误差较大,不能满足一些高精度场景的需求。为此可考虑在地面布设伪卫星,优化几何布局[2],建立区域伪卫星增强的北斗系统,以满足特殊环境下的应用需求。其中,伪卫星着陆系统具有机动灵活、抗干扰性能好、成本低等优点,可以辅助增强北斗系统[3]。
用户通过接收机的自主完好性(RAIM)来监测系统的完好性,导航系统中配置的伪卫星不仅能够优化空间星座几何布局,提高定位精度,还能够提供额外观测量,有效改善系统完好性[4]。在由于地理环境遮挡或电磁干扰等而导致的卫星信号失效的恶劣情况下,利用多颗伪卫星进行独立定位,基于各观测量之间一致性的原理,用户仍然能够在异常情况下提供告警,自主进行故障检测与识别,完成导航定位服务,以保障系统完好性服务[5]。
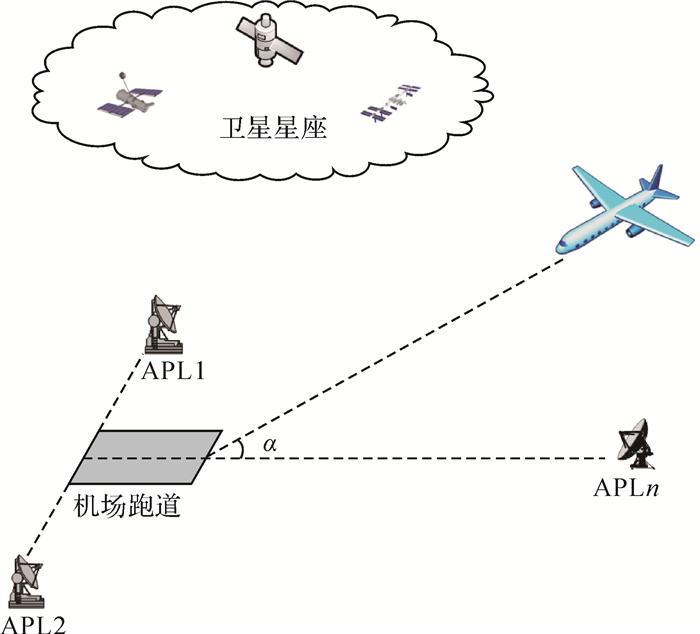
一、 伪卫星辅助北斗定位模型伪卫星辅助北斗定位的定位模型如图 1所示,地面伪卫星能发出空间北斗卫星相同格式的导航信号,用户同时接收地面伪卫星和空间导航卫星信号,并根据两类观测信号不同的误差特性进行联合解算,不但可以提高北斗系统独立定位下的导航精度,而且为导航解算增加了更多的观测量,提高了系统故障检测和识别的能力[6]。
|
| 图 1 伪卫星辅助北斗定位模型示意图 |
在伪卫星增强北斗定位系统中,根据伪卫星组网方式与系统结构的不同,可能有不同的解算方案。伪卫星辅助北斗定位时,用户同时接收其伪距观测模型与伪卫星独立定位下观测模型相似,接收机在进行伪距误差修正后,可获得定位解算的线性化方程,可表示为[7]
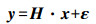 (1)
(1) n维矢量y和噪声矢量ε均与M个可视北斗卫星和N个伪卫星的观测量有关,且M+N=n。n×4的方向余弦向量H由两部分组成,包括高空北斗卫星和地面伪卫星
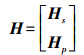 (2)
(2) 其中,伪卫星观测矩阵Hp可表示为
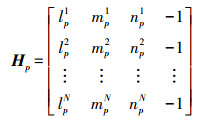 (3)
(3) 卫星观测矩阵Hs可用相同方式获得,各卫星位置由播发的导航电文计算得到。
利用最小二乘法可求解伪卫星辅助北斗定位下的用户位置为
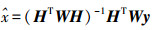 (4)
(4) 式中,W=diag (1/σs2, …, 1/σs2, 1/σp2, …, 1/σp2),为加权对角阵,σs、σp分别为卫星与伪卫星的等效测距误差。
对于卫星观测量,其误差分量包含卫星星历星钟误差、传播电离层对流层误差、多径和接收机噪声等。而对于伪卫星观测量,考虑到伪卫星一般固定安装在地面,不存在卫星星历误差和电离层延迟误差,同时假设所有伪卫星发射机使用共同时钟,以消除相对时钟误差。因此一般认为伪卫星观测量的等效测距误差要小于高空区域的导航卫星。
二、 伪卫星辅助北斗定位的故障检测与识别算法北斗导航卫星位于2万~3万千米高空,而地面伪卫星与用户间的距离往往最多只有几十到上百千米,在伪卫星辅助北斗定位下,应考虑导航卫星与伪卫星测距精度不同,当卫星与伪卫星发生相同故障偏差时,由于伪卫星距离用户更近,测距误差也更小,相对于卫星故障更容易检出。当测距误差较小的伪卫星发生故障时,产生的测距偏差较小,若使用传统的奇偶矢量法进行完好性检测,由于测距误差较大的卫星观测量的存在,使得算法对于较小测距误差伪卫星的敏感度降低,故障检测概率降低。
考虑对式(1)观测方程进行加权[8-9],方程左右两侧乘以权值变换矩阵D,可得
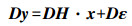 (5)
(5) 式中,变换矩阵D=diag (1/σs, …, 1/σs, 1/σp, …, 1/σp),即W=DTD。
对加权后的观测矩阵进行QR分解,即将观测量的测量误差包含到奇偶矢量p中,由此可以重新构造加权奇偶矢量
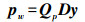 (6)
(6) 因此,可得到各伪距的残差平方和为SSE=pwTpw。无故障观测量时,加权奇偶矢量pw的各分量相互独立,且服从标准正态分布,则各伪距的残差平方和服从χ2(n-4)分布。而有故障观测量存在时,SSE服从非中心的χ2(n-4)分布。可确定故障检测量的检测门限T,通过判断归一化的伪距残差平方和与检测门限的大小,即可判断当前时刻是否包含故障观测量。
同理,若检测到当前时刻包含故障观测量,利用下式对故障卫星和伪卫星进行识别,即可剔除当前故障观测量[10]
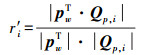 (7)
(7) 通过判断各相关系数r′i的大小,相关系数r′i最大且接近于1对应的观测量即为故障观测量,在定位解算过程中应当剔除。
三、 伪卫星辅助北斗定位的完好性保护级计算方法不同仰角的卫星信号穿过大气层的角度不同,伪距测量误差各异,而伪卫星与卫星观测量的测量精度差异更为明显,基于加权最小二乘的原理,不仅应该在定位解算时考虑各观测量的权值不同,而且在进行完好性监测时同样应考虑各观测量的精度差异。
加权最小二乘定位模式下,若第i颗卫星发生故障,导致的伪距偏差为bi,则由此故障引起的水平定位误差为
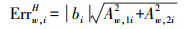 (8)
(8) 式中,Aw=(HTWH)-1HTW,Aw, 1i和Aw, 2i分别为矩阵Aw的第1行第i列和第2行第i列元素。相应的,忽略观测噪声的影响,利用伪距残差平方和作为检验统计量时,该故障条件下的检验统计量为
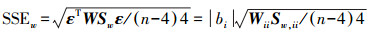 (9)
(9) 式中,Sw=E-H(HTWH)-1HTW;Wii为加权矩阵W的第i个对角线元素;Sw, ii是投影矩阵Sw的第i个对角线元素。由此,可得到与每个观测量关联的斜率为
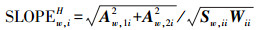 (10)
(10) 由此可得加权最小二乘模式下的完好性误差保护级xPLw为
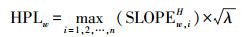 (11)
(11) 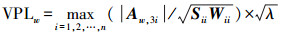 (12)
(12) 通过定位误差保护级与相应的误差保护限值HAL、VAL比较,即可获得完好性故障检测的可用性保证。
四、 仿真分析伪卫星辅助北斗定位模式下,空间用户同时接收地面伪卫星和空间卫星信号。假设该中原地区用户由于地形或遮挡物的影响,仅能全天候不间断观测到5颗北斗GEO卫星,尽管满足4颗卫星定位的最低要求,但由于其卫星几何构型太差,定位精度无法满足航空用户的一般要求。考虑增设地面伪卫星辅助北斗系统定位,在同一区域布设3颗以上的地面伪卫星,设置误警概率和漏检概率分别为10-7和10-3,导航卫星和地面伪卫星的等效测距误差分别取6 m和4 m,卫星截止高度角为5°,分析加入伪卫星辅助定位后对系统完好性保护级的影响。
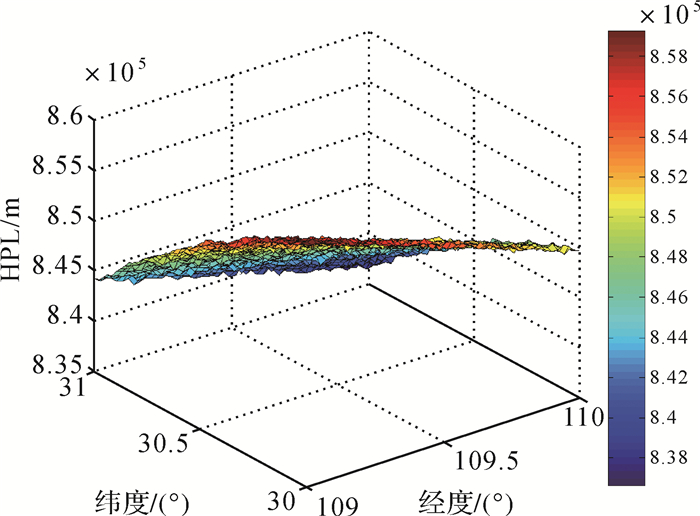
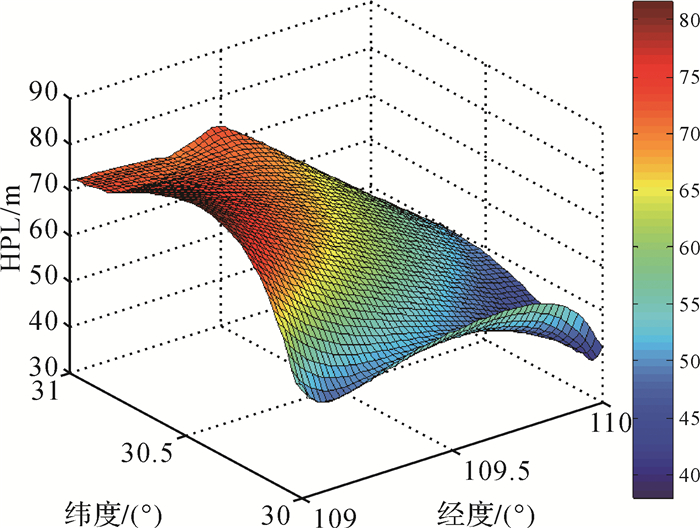
如图 2所示,对于该中原区域内用户,当只能观测到5颗北斗GEO卫星时,不仅卫星几何构型不佳,定位精度差,而且其水平保护级HPL值达到了上千千米,远不能满足完好性检测的可用性要求。而加入3颗伪卫星后,区域内水平保护级HPL分布如图 3所示,其最大值不到80 m,满足非精密进近NPA的完好性需求。
|
| 图 2 不加入伪卫星时HPL分布情况 |
|
| 图 3 加入3颗伪卫星后HPL分布情况 |
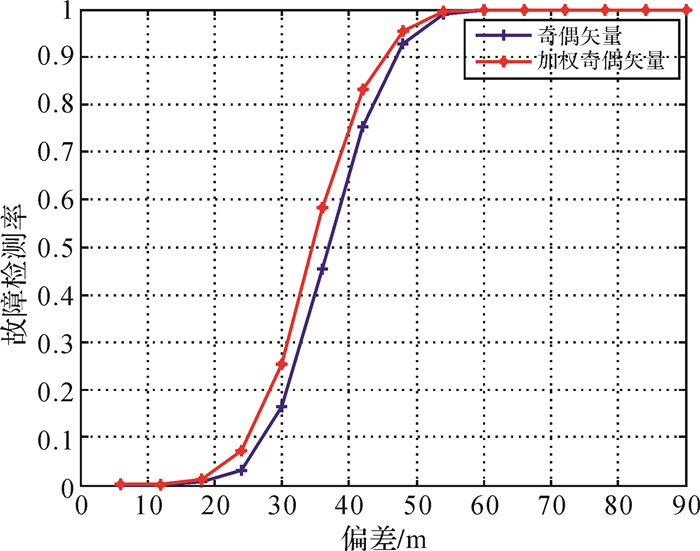
下面分析伪卫星辅助定位模式下的故障检测能力,假定用户在最后进近着陆阶段以匀速直线运动下滑到机场跑道,速度v=60 m/s,下滑角为3°,用户初始位置为(110°E,30.5°N,5000),给其中的5号星加入一定大小的故障偏差,分析上文给出的加权奇偶矢量法的故障检测性能,仿真结果如图 4所示。
|
| 图 4 两种故障检测算法的故障检测性能对比 |
两种故障检测算法的检测性能如图 5所示,细点划线表示常规奇偶矢量法的故障检测性能,粗点线表示加权奇偶矢量的故障检测性能。两种故障检测算法对于小故障偏差都不敏感,而对于故障偏差较大时,加权奇偶矢量法的检测性能岷县优于常规奇偶矢量法。在故障偏差达到10时,即可达到100%的故障检测能力。

|
| 图 5 两种HPL算法的RAIM可用性对比 |
两种HPL算法的RAIM可用性对比如图 4所示,细线表示在整个飞行阶段常规HPL算法得到的HPL值,粗线表示加权HPL算法得到的HPL值。由图中可知,加权HPL可获得相比于传统HPL算法更小的HPL值,因此可在一定程度上提高RAIM算法的可用性。
五、 结束语针对伪卫星辅助北斗定位模式,本文给出了一种考虑观测量不同精度的加权RAIM算法。仿真结果表明,加入伪卫星观测量,能有效降低系统完好性保护级xPL,提高系统可用性。在当前时刻各观测量精度存在明显差异时,加权奇偶矢量法能有效提高对测距误差较小观测量的敏感度,有效提高系统的可靠性。
| [1] | 侯勇, 赵凯印. 伪卫星的远近效应研究[J]. 电脑知识与技术 , 2014, 10 (1) : 216–218. |
| [2] | 桑文刚, 何秀凤, 陈永奇. 基于精度因子几何结构的独立伪卫星布局研究[J]. 测绘通报 , 2013 (9) : 1–4. |
| [3] | 籍利平. 基于北斗导航卫星的伪卫星技术在区域定位中的应用[J]. 测绘科学 , 2002, 27 (4) : 53–56. |
| [4] | 郭睿, 张健铤. 伪卫星增强条件下的RAIM算法可用性及性能分析[J]. 天文学进展 , 2009, 27 (1) : 89–97. |
| [5] | 朱祥维, 徐博, 李井源, 等. 基于广义伪卫星的新一代GNSS增强系统[J]. 测绘通报 , 2016 (2) : 1–7. |
| [6] | 耿建平, 唐先红.第二代北斗卫星导航系统伪卫星辅助定位技术研究[C]//2010第一届中国卫星导航学术年会.北京:[s.n.], 2010. http://www.wenkuxiazai.com/doc/13d1137a31b765ce050814c6.html |
| [7] | 郭睿, 郑勇, 骆亚波, 等. 伪卫星技术及应用[J]. 军事测绘 , 2005 (64) : 21. |
| [8] | 杨永波, 刘峻宁, 张黎. 基于总体最小二乘法的RAIM算法研究[J]. 城市勘测 , 2009 (6) : 55–57. |
| [9] | HATCH R, SHARPE T, YANG Y C.A Simple RAIM and Fault Isolation Scheme[C]//Proceedings of ION GPS 2003.[S.l.]:[s.n.], 2003. |
| [10] | 陈金平.GPS完善性增强研究[D].郑州:信息工程大学, 2001. |


