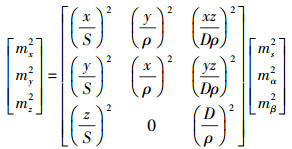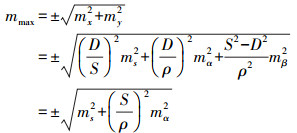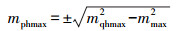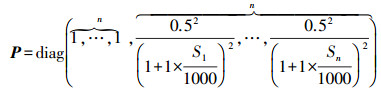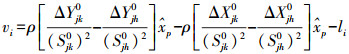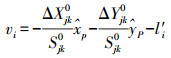2. 武汉市桥梁工程有限公司, 湖北 武汉 430070 ;
3. 大汉阳现代有轨电车试验线BT公司, 湖北 武汉 430050
在变形监测领域,测量机器人的出现,使得监测数据的获取朝着自动化、智能化、系统化的方向发展。而设站点的平面坐标误差在变形监测数据采集过程中会传递给目标点,因此设站点的点位不能任意选取,需要了解基准点附近自由设站点的点位误差分布情况。
在变形监测工程中,一般会设置多个基准点(大于3个)和若干设站点[1],基准点作为参考点,设站点位于变形体上,通常会发生移动。利用自由设站方法[2],在开始目标点的测量之前,先精确计算设站点的平面坐标,如果坐标精度合格则进行后续目标点的监测和分析计算。在不同应用领域中,徕卡测量机器人TS30超高精度全站仪采用自由设站法,能够达到1~2 mm的精度,满足变形监测的精度要求,在管线闸道变形观测中取得了良好的效果[3];通过对基坑边坡水平位移监测工作进行评估,TS30测量机器人能够让精度要求极高的基坑监测工作变得简单起来[4];在地铁隧道自动化监测过程中,采用自由设站的边角后方交会方式,通过计算不同数目控制点下设站点坐标改正,得到TM30 0.5″仪器能够提高的相对精度[5]。
在分析自由设站点坐标误差的过程中,对于3个控制点的情况,若采用方向后方交会法,则存在危险圆的问题[6],即如果设站点与控制点在同一外接圆上,那么设站点的误差将为无限大,但当设站点位于控制点所围成的三角形内切圆的圆心时,设站点的点位误差最小,此时为最佳设站点[6]。边角后方交会法中如果测量边长大于控制点边长,方程的解会有多重性[7]的问题。通过边角后方交会计算公式容易获得两个基准点情况下设站点的误差等值图[8],但是对于多个基准点的情况根据公式获得等值图的过程较为繁琐。TS30[9]能够对基准点同时进行方向和距离的精确观测,但从参数求解的公式直接分析设站点位中误差分布规律的过程较为繁琐。本文通过在基准点周围计算格网分布各自由设站点位中误差,绘制中误差等值图,从而进一步分析设站平面点位误差分布情况。根据测量规范中目标点的平面点位精度要求及测量过程中的测量误差计算设站点的误差范围,结合设站点位中误差等值图可以选择合适的自由设站范围。
一、 自由设站平面点位精度要求设测量过程中水平角为α,竖直角为β,斜距为S,并令平距D=Scosβ,假设设站点无误差,则目标点点位误差计算[10]如下
式中,mS、mα、mβ分别表示测量过程中斜距、水平角、竖直角中误差。假设mα=mβ,则可知当S=D时,测量过程中最弱目标点的测量中误差mmax存在,且
设工程测量规范或项目设计书中对于目标点的点位平面误差要求为mqhmax,则相应的设站点点位平面中误差也存在一个最大值,设为mphmax,且满足
根据TS30不同测量(测角测距)模式,在最大测程3500 m范围内mmax与观测距离S的关系见表 1。
| S/m | mS/mmax | |||
| mα:0.5″, 0.6 mm+1×10-6 D | mα:1.0″,0.6 mm+1×10-6 D | mα:0.5″,1 mm+1×10-6 D | mα:1.0″,1 mm+1×10-6 D | |
| 100 | 0.7/0.70 | 0.7/0.70 | 1.1/1.10 | 1.1/1.10 |
| 500 | 1.1/1.10 | 1.1/1.10 | 1.5/1.50 | 1.5/1.50 |
| 1000 | 1.6/1.60 | 1.6/1.60 | 2.0/2.00 | 2.0/2.00 |
| 1500 | 2.1/2.10 | 2.1/2.10 | 2.5/2.50 | 2.5/2.50 |
| 2000 | 2.6/2.60 | 2.6/2.60 | 3.0/3.00 | 3.0/3.00 |
| 2500 | 3.1/3.10 | 3.1/3.10 | 3.5/3.50 | 3.5/3.50 |
| 3000 | 3.6/3.60 | 3.6/3.60 | 4.0/4.00 | 4.0/4.00 |
| 3500 | 4.1/4.10 | 4.1/4.10 | 4.5/4.50 | 4.5/4.50 |
以测角精度mα=0.5″,测距精度1 mm+1×10-6D的测量模式为例,表 2计算了在不同测量距离及不同目标点精度要求下自由设站点的平面点位中误差。
| mm | ||||||||||
| S/m | mmax | mqhmax | ||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | ||
| 100 | 1.10 | 1.67 | 2.79 | 3.85 | 4.88 | 5.90 | 6.91 | 7.92 | 8.93 | 9.94 |
| 500 | 1.50 | 1.32 | 2.60 | 3.71 | 4.77 | 5.81 | 6.84 | 7.86 | 8.87 | 9.89 |
| 1000 | 2.00 | 0.00 | 2.24 | 3.46 | 4.58 | 5.66 | 6.71 | 7.75 | 8.77 | 9.80 |
| 1500 | 2.50 | 0.00 | 1.66 | 3.12 | 4.33 | 5.45 | 6.54 | 7.60 | 8.65 | 9.68 |
| 2000 | 3.00 | 0.00 | 0.00 | 2.65 | 4.00 | 5.20 | 6.32 | 7.42 | 8.49 | 9.54 |
| 2500 | 3.50 | 0.00 | 0.00 | 1.94 | 3.57 | 4.87 | 6.06 | 7.19 | 8.29 | 9.37 |
| 3000 | 4.00 | 0.00 | 0.00 | 0.00 | 3.00 | 4.47 | 5.74 | 6.93 | 8.06 | 9.17 |
| 3500 | 4.50 | 0.00 | 0.00 | 0.00 | 2.18 | 3.97 | 5.36 | 6.61 | 7.79 | 8.93 |
基准点附近设站点点位中误差等值图绘制过程如下。
1) 设置测角中误差为0.5″,并作为后验单位权中误差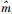
2) 根据经典间接平差求解过程[11],求得参数X协因数矩阵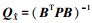
对于边长观测值,其误差方程为
因为这里并没有进行参数的求解过程,只考虑中误差传播过程,因此要把B中用于观测方程单位同一化用的常数ρ省略。
3) 根据公式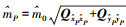
4) 重复以上过程,在基准点周围计算格网分布各点的平面点位中误差。
5) 根据格网中误差数据并利用Matlab绘制基准点中误差等值图。
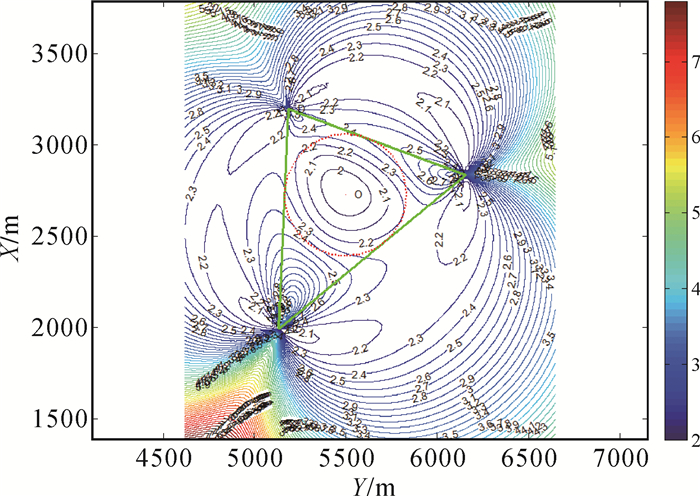
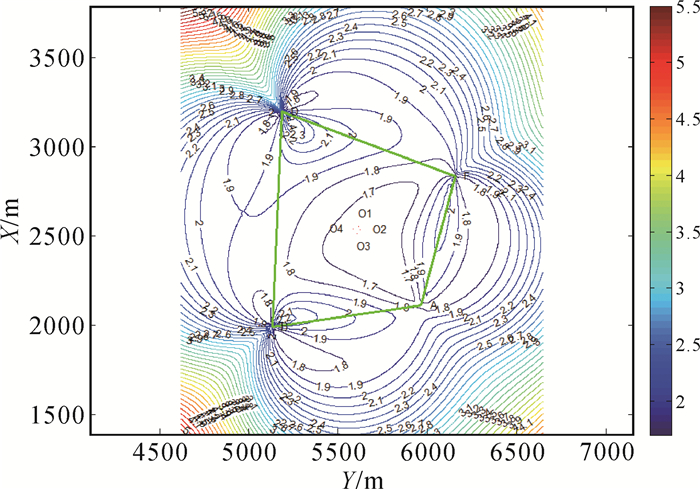
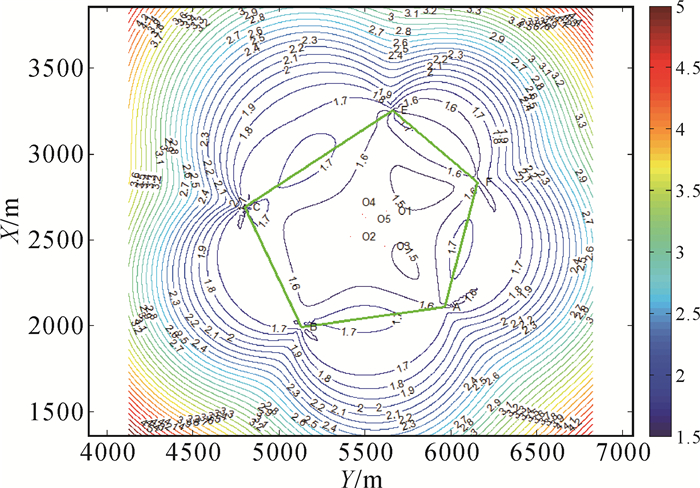
任意选取平面坐标如表 3所示的6个基准点,根据以上过程绘制了采用3、4、5、6个基准点设站的点位误差等值图,如图 1-图 4所示。
| m | ||
| 点号 | X坐标 | Y坐标 |
| A | 2 110.593 | 5 965.422 |
| B | 1 992.765 | 5 132.304 |
| C | 2 692.201 | 4 803.153 |
| D | 3 197.583 | 5 187.635 |
| E | 3 253.235 | 5 662.136 |
| F | 2 837.445 | 6 156.289 |
|
| 图 1 3个基准点下的设站点误差等值图 |
|
| 图 2 4个基准点下的设站点误差等值图 |
|
| 图 3 5个基准点下的设站点误差等值图 |

|
| 图 4 6个基准点下的设站点误差等值图 |
1) 点位误差分布以基准点外围图形的每条边的中垂线为对称轴呈对称分布,且在外围图形外侧随着距该边距离的增大,点位中误差逐渐增大;在外围图形内侧随着距该边距离的增大,点位中误差逐渐减小,但增减缓慢。
2) 点位误差分布以内心与各基准点连线为对称轴呈对称分布,且在外围图形外侧随着距该基准点距离的增大,点位误差逐渐增大;在外围图形内侧随着距该基准点距离的增大,点位误差逐渐减小,但增减迅速。
3) 为提高设站点精度,设站点应尽量位于外围图形内侧并远离基准点。
4) 与方向后方交会情况类似,点位误差最小的点,即最佳设站点的位置在基准点外围图形内侧的内心附近(图中O点附近)。
以图 2为例,并结合表 1对需要达到的设站精度进行了统计,以此来说明各设站精度的设站空间范围。设站范围表示为小于该设站精度的空间范围面积与中误差等值图总范围面积的比值,具体数值见表 4,由此可以得到对某个精度要求的设站范围的大小。
| (%) | ||||||||||
| S/m | mmax/mm | 设站范围 | ||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | ||
| 100 | 1.10 | 0.00 | 60.83 | 85.86 | 95.35 | 98.02 | 99.29 | 100.00 | 100.00 | 100.00 |
| 500 | 1.50 | 0.00 | 53.55 | 83.82 | 94.77 | 97.89 | 99.22 | 100.00 | 100.00 | 100.00 |
| 1000 | 2.00 | 0.00 | 24.04 | 79.30 | 93.56 | 97.66 | 99.07 | 99.99 | 100.00 | 100.00 |
| 1500 | 2.50 | 0.00 | 0.00 | 70.82 | 91.38 | 97.29 | 98.87 | 99.90 | 100.00 | 100.00 |
| 2000 | 3.00 | 0.00 | 0.00 | 55.61 | 87.80 | 96.66 | 98.59 | 99.76 | 100.00 | 100.00 |
| 2500 | 3.50 | 0.00 | 0.00 | 0.11 | 81.49 | 95.30 | 98.26 | 99.57 | 100.00 | 100.00 |
| 3000 | 4.00 | 0.00 | 0.00 | 0.00 | 67.52 | 92.66 | 97.78 | 99.31 | 100.00 | 100.00 |
| 3500 | 4.50 | 0.00 | 0.00 | 0.00 | 12.99 | 87.43 | 97.09 | 98.96 | 99.99 | 100.00 |
由表 4可以看出,随着对设站精度要求的提高,可以用于设站的范围逐渐减小,如果某一变形监测项目对设站点的点位精度有比较高的要求,则可以通过相应的设站点点位中误差等值图寻找最佳设站位置,有时可能不存在这样的设站位置,此时需要考虑重新布设基准点的位置或改变测量模式来提高测量精度。如果对设站点的点位精度要求不是很高,则可以进一步从原始等值图中提取某一误差对应的单条误差等值线并根据该等值线范围确定设站范围,同时在该范围内还可以结合其他地形因素或不利于设站的干扰因素确定可以用于设站的位置。
构建基准点附近设站点位中误差等值图的目的是可以在变形监测工程施工前对设站点和基准点的位置进行模拟,基于目标点的精度要求和测量误差对设站点位置的选取进行可行性分析;同时规划出用于变形监测的设站点的设站范围。
四、 结束语本文基于目标点的点位精度要求及测量过程中中误差的传播规律,采用绘制中误差等值图的方式,分析了在基准点附近进行自由设站时设站点的点位中误差分布规律。采用这种绘图方式能够脱离复杂公式的束缚,直观获得最佳设站点或最佳设站范围,在该范围内可以进一步结合基准点附近的地形分布及影响设站的环境因素,能够进一步指导在有利地形设站。
本文假设基准点是没有误差的,对于考虑基准点点位误差的情况需要进一步分析讨论。
| [1] | 张正禄, 李广云, 潘国荣. 工程测量学[M]. 武汉: 武汉大学出版社 ,2005 : 180 . |
| [2] | 潘正风, 程效军, 成枢. 数字测图原理与应用[M]. 武汉: 武汉大学出版社 ,2009 : 201 -203. |
| [3] | 王洪. 徕卡TS30超高精度全站仪在变形监测中的应用[J]. 辽宁工程技术大学学报(自然科学版) , 2015 (3) : 401–404. |
| [4] | 易致礼, 张维, 李宝安. 徕卡TM30精密监测机器人在基坑边坡水平位移监测中的应用[J]. 测绘通报 , 2014 (S2) : 19–22. |
| [5] | 吴灿鑫, 胡雷鸣, 付和宽. 地铁隧道自动化监测精度分析[J]. 测绘通报 , 2015 (1) : 137–138. |
| [6] | 严伯铎. 后方交会的优化及最佳几何图形[J]. 勘察科学技术 , 2000 (4) : 46–50. |
| [7] | 李全信. 边角后方交会的精度分析及布设方案选择[J]. 测绘工程 , 2000 (3) : 48–52. |
| [8] | 崔有祯, 韩光瞬, 李文杰. 边角后方交会最优图形与精度分析[J]. 北京测绘 , 2011 (3) : 89–90. |
| [9] | 杨俊志. 常用大地测量仪器名称及相关术语的标准化[J]. 测绘通报 , 2004 (2) : 65–66. |
| [10] | 曾勇.基于TS30测量机器人地壳形变自动数据采集系统的研究与应用[D].西安:西安科技大学, 2014:28-29. http://cdmd.cnki.com.cn/Article/CDMD-10704-1014072729.htm |
| [11] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社 ,2009 : 123 . |