2. 31009部队, 北京 100088 ;
3. 北京大学工学院, 北京 100871 ;
4. 中国科学院地理科学与资源研究所, 北京 100101
在面向移动单元的遥感影像服务中,信息分发信道窄严重制约了遥感信息的应用发展,对于移动单元所关注的高价值目标信息,需要一种根据信息价值权重进行自适应压缩的方法。面向上述需求,利用数学形态学方法进行感兴趣区域快速提取,并基于价值权重进行自适应压缩,解决窄带宽条件下高价值遥感影像的提取和压缩问题,为遥感影像直接、快速、高效地支持移动单元提供技术支撑。
近年来不少学者研究了感兴趣区提取及压缩算法,李晓飞等通过形态学运算强化特定结构的多个目标区域,运用阈值分割算法完成了图像区域分割[1];杜维涛等以边缘梯度方向为图像分割的准则,提取了图像的边缘区域和纹理区域,采用通用部分位平面偏移方法进行了感兴趣区编码,并采用SPIHT编码进行了压缩[2];邰华凤等在小波变换的基础上,将小波系数划分为ROI系数和BG系数,然后将ROI系数进行编解码,得到了较高图像质量的ROI区域图像[3]。
本文结合上述方法,经过多次试验,运用数学形态学等方法对上述算法进行整合改进,实现感兴趣区提取,并采用JPEG2000中的感兴趣区编码和SPIHT编码对影像进行压缩编码,模拟移动服务中渐进传输的全过程,发展出一套面向移动服务的遥感影像感兴趣区全流程自动提取压缩重构方法。
一、 算法思路人们往往只对影像中的部分区域感兴趣,因此可以对这些区域采用无损或近无损的方法进行压缩,感兴趣区之外可采用高压缩比处理,在保证不丢失重要信息的同时,又能有效地压缩数据。将基于感兴趣区的编码方法与渐进传输结合起来,使得用户不必完全接收整幅影像就可以清晰地浏览影像中感兴趣部分的内容,能更好地满足用户的需求。
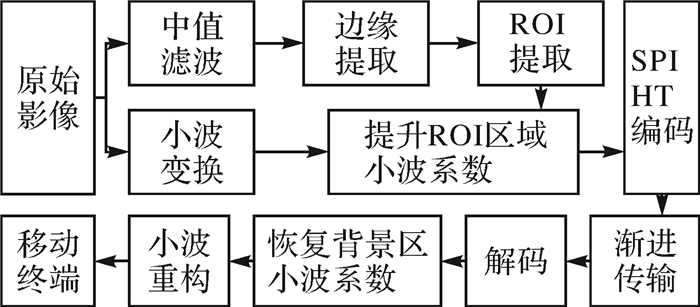
算法思路如图 1所示:①对原始图像进行n层小波分解变换;②通过形态学运算得到ROI区域,生成ROI掩模;③在小波系数矩阵中,提升ROI区域小波系数;④使用SPIHT算法进行压缩编码;⑤码流渐进传输,可在任何位置打断,但打断前收到编码越多,解码后图像质量更好;⑥对解码后的小波系数,根据ROI掩模恢复背景区域的小波系数;⑦通过小波重构获得结果图像,移动端完成接收。
|
| 图 1 遥感影像感兴趣区提取压缩算法思路 |
腐蚀和膨胀是数学形态学的两种基本运算,并发展出开运算和闭运算两个重要函数,都以集合的形式进行运算。设A为影像,B为结构元素,则A对B腐蚀定义为
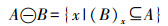 (1)
(1) A被B膨胀的定义为
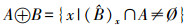 (2)
(2) 式中,x是一个表示集合平移的位移量。腐蚀是一种收缩变换,膨胀是一种扩张变换。开运算定义为
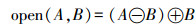 (3)
(3) 闭运算定义为
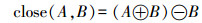 (4)
(4) 开运算使影像变小,闭运算使影像增大[4]。
1. 数学形态学与中值滤波进行边缘提取中值滤波是基于排序的非线性滤波的典型,保留影像结构的同时可以消除噪声。选择模板在影像中漫游,读取模板下对应像素的灰度值,找到灰度值的中位数并将这个中位数赋给模板中心位置的像素。
采用中值滤波与数学形态学结合的方法进行边缘提取,具体步骤如下:①使用3×3的中值滤波模板进行中值滤波,影像高频噪声被去除,影像边缘信息被保护;②对影像进行腐蚀运算,使影像边缘上的灰度得到加强,如图 2所示;③用原影像减去腐蚀后的影像,从而得到影像的边缘,如图 3所示。设原影像为F,滤波后输入的影像为A,B为结构元素,则A被B腐蚀

|
| 图 2 腐蚀运算边缘检测原理 |

|
| 图 3 原始影像及边缘检测 |
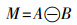 (5)
(5) 利用原图减去腐蚀后的影像,则可获得影像的边缘
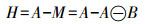 (6)
(6) 此影像上每一个灰度级代表不同等级的边缘点,灰度值越高边缘越明显。
2. 数学形态学进行感兴趣区提取对影像分块,计算块内边缘点的数量,如果小于一定的阈值t,定义为背景区(BG);大于t,则定义为感兴趣区(ROI)。Sum (Grad)为边缘点的数量,一般取t=0.05。分块大小与压缩时小波分解的层数有关。小波分解的层数为n,则块大小不应小于2n×2n。将小波分解的层数定为4,故每一小块大小为16×16。
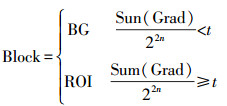 (7)
(7) 边缘点数量判断的ROI区域很杂乱,没有形成区域状,需采取数学形态学中开运算和闭运算结合的开闭运算混合滤波方法对影像进行处理。先进行闭运算,去掉中间的空洞并填补轮廓上的缝隙;再进行开运算,去掉ROI区域中细的突出;由此形成一个规则完整的ROI区域。如图 4所示,与原始影像对比发现,建筑物被清晰地提取出来。

|
| 图 4 边缘点数量判断的ROI区域及形态学后处理 |
获得ROI区域后,小波变换编码无法直接使用,必须转成小波变换相应层数的ROI掩模。对每个ROI点,根据它在原始影像中的比例位置,分别求出N级小波变换形成的3N+1个子带中的相对位置。这种方法没有考虑具体滤波器的操作,并不能保证能获得所有与ROI相关的系数,特别是边缘可能有小部分损失,但这并不影响ROI的编码质量。因此,采用简单的递推法,但却降低了ROI掩模生成的复杂性。
JPEG2000压缩标准中定义了感兴趣区编码方法,规定了两种标准算法:一种是基于缩放的一般方法,另一种是最大位移方法,均通过按比例缩小背景区系数实现,使得感兴趣区系数相比于背景区系数位于更高的比特平面[2]。在熵编码时,感兴趣区系数将比背景区域系数优先进行编码并组织码流。在面向移动服务的渐进传输中,感兴趣区比背景区更精确地优先传输给解码器,由此获得保留更多感兴趣区信息前提下的高压缩性能。
二维离散小波变换可以将二维影像在不同的尺度上进行分解,得到近似分量LL,水平细节分量LH、垂直细节分量HL、对角细节分量HH;再对LL进行分解得到第二级小波变换,依此类推。对影像进行4级小波变换,得到同样大小的小波系数矩阵,如图 5所示。

|
| 图 5 4层小波分解掩模及分解影像 |
用影像作为底面,表示像素亮度大小的8位二进制数作为高度,形成一个立体直方图,各像素位置相同的位形成一个平面,称为位平面。位平面平移是二进制数小数点的平移,即将小波系数背景区的值除以2n,n的值由位平移算法决定。为简化算法,在ROI掩模中,将背景区的小波系数除以22,即通过简单位平面平移方法,获得ROI编码。
2. 子带编码、解码与重构子带编码采用基于嵌入式零树编码思想的SPIHT算法,它将某一树节点及其所有后继节点划归为同一集合,并采用适当的集合分割排序策略,通过初始化、排序过程、细化过程和量化步长更新等4个子工程,完成嵌入编码[2]。SPIHT编码在系数子集的分割和重要信息的传输方面采用了独特的方法,能够实现幅值大的系数优先传输的同时,隐式地传送系数的排序信息,具有较高的峰值信噪比(PSNR)和较好的影像复原质量,是一种适合于感兴趣区压缩的编码方法。SPIHT算法请参考相关文献。
通过上述编码,形成了一系列由0和1构成的二进制码流。解码是编码的逆过程,将编码算法的输入和输出调换,就是解码算法。解码的精度与编码的级数有关。在码流传输过程中,影像是逐渐变清晰的。假如对小波系数矩阵进行了10级编码,传输过程按1、2、…、10级的顺序进行,每传到一级都可以获得一个重构影像,10级解码会获得比1级解码更好的重构影像,即重构影像的质量随着码流的渐进传输越来越好。面向移动单元的服务中,信息分发信道窄的条件下,上述渐进传输的方法可让用户先看到高价值目标信息,再逐渐看到完整影像。为节省流量,也可以提前中断解码过程,并不影响用户接收高价值目标信息。
为保证小波重构能够跟原始影像接近,需将背景区域的小波系数乘以22,恢复到原始数值,实现背景区小波系数的恢复。将小波系数矩阵进行小波逆变换,恢复为重构影像。原始影像采用Daubechies 9/7双正交小波,对影像进行4级小波分解,10级SPIHT编码。如图 6所示,模拟渐进传输的过程中进行解码重构,影像的质量越来越好,符合渐进传输的特点,ROI区比背景区具有更好的重构质量。

|
| 图 6 影像渐进传输模拟过程 |
引入两个概念对试验结果进行分析,峰值信噪比(PSNR)和影像压缩比。PSNR为衡量经过处理后的影像品质,值越大代表失真越少,计算公式为
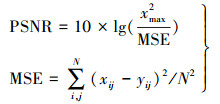 (8)
(8) 式中,xmax为8 bits表示法的最大值255;MSE为mean square error,均方误差;xij与yij表示原影像和重构影像上(i, j)点处的灰度值;PSNR的单位为dB。影像压缩比指原影像大小比值压缩后大小,压缩比越大说明压缩效果越好。分别计算ROI和背景区的PSNR,获得影像渐进传输中影像质量变化情况见表 1。
| 解码级数 | ROI PSNR | BG PSNR | 解码级数 | ROI PSNR | BG PSNR |
| 1 | 5.251 6 | 5.370 6 | 6 | 15.899 1 | 9.382 3 |
| 2 | 6.159 3 | 5.464 7 | 7 | 16.418 4 | 11.451 9 |
| 3 | 8.066 2 | 5.813 1 | 8 | 16.607 9 | 12.514 6 |
| 4 | 11.730 7 | 6.219 6 | 9 | 16.682 3 | 12.983 4 |
| 5 | 14.524 7 | 7.269 | 10 | 16.697 9 | 13.166 2 |
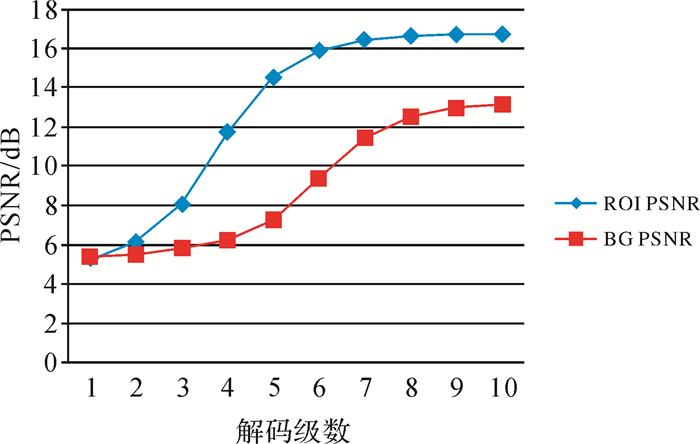
如图 7所示,ROI区的PSNR值高于背景区,并随着码流的传输相差逐渐拉大,而后又逐渐趋近。ROI比背景区获得了更好的重构效果,随着重构级数的上升,背景区的PSNR也逐渐上升,但ROI区始终有比背景区更好的重构质量。
|
| 图 7 影像渐进传输过程中PSNR值比较 |
采用Daubechies 9/7双正交小波,对影像进行4级小波分解,分别进行10、11、12级SPIHT编码和同样级数的解码,进行压缩比和不同编码级别影像质量评价(见表 2)。随着编码级数的增加,压缩率逐渐增加,PSNR也逐渐增加,影像质量逐渐变高。一般来说,当PSNR达到30时,人眼已经难以分辨重构影像与原影像的不同,那么11级编码已经足以符合要求,其压缩比为2.7,这样的压缩比是可观的。
| 编码解码级数 | 原始大小/bit | 压缩大小/bit | 压缩比 | ROI PSNR |
| 10级 | 512×512×8 | 567 854 | 3.69 | 16.697 9 |
| 11级 | 512×512×8 | 776 255 | 2.70 | 48.532 2 |
| 12级 | 512×512×8 | 933 465 | 2.24 | 54.207 5 |
经过上述试验验证得知,本方法实现了遥感影像的ROI区提取、压缩编码、解码重构的全自动流程,保留了高价值目标信息,且较高的压缩比有利于遥感影像在带宽有限条件下传输,并节约大量存储空间,将能够促进遥感影像在移动服务中的普及应用。
| [1] | 李晓飞, 马大玮, 范小麟, 等. 基于数学形态学的遥感图像多感兴趣区域提取[J]. 计算机技术与发展 , 2007, 17 (12) : 56–59. |
| [2] | 杜维涛, 刘方, 陶永宽, 等. 一种遥感图像多级感兴趣区域的压缩方法[J]. 计算机仿真 , 2008, 25 (9) : 215–219. |
| [3] | 邰华凤, 黄大庆. 基于小波变换的感兴趣区域图像压缩算法[J]. 苏州科技学院学报(自然科学版) , 2010, 27 (3) : 51–54. |
| [4] | 王慧锋, 战桂礼, 罗晓明. 基于数学形态学的边缘检测算法研究及应用[J]. 计算机工程与应用 , 2009, 45 (9) : 223–226. |
| [5] | 梁燕, 刘文耀, 郑伟. 实现感兴趣区域编码的通用部分位平面偏移法[J]. 光电子·激光 , 2004, 15 (11) : 1334–1338. |
| [6] | 强永刚, 殷建平, 祝恩, 等. 基于小波变换和数学形态学的遥感图像人工建筑区提取[J]. 中国图象图形学报 , 2008, 13 (8) : 1459–1464. |
| [7] | 万红林, 焦李成, 王桂婷, 等. 在感兴趣的区域层面上进行SAR图像变化检测的方法研究[J]. 测绘学报 , 2012, 41 (2) : 239–245. |
| [8] | 王晓芳, 邱书波, 张绪光. 基于小波变换的ROI图像压缩改进算法研究[J]. 计算机工程与科学 , 2010, 32 (8) : 84–133. |
| [9] | 席志红, 许新利, 刘利彬. 基于SPIHT算法的感兴趣区域编码的研究[J]. 应用科技 , 2007, 34 (1) : 31–34. |
| [10] | 卓力, 沈兰荪, KIN-MANL. 基于感兴趣区的图像编码与渐进传输[J]. 电子学报 , 2004, 32 (3) : 411–415. |


