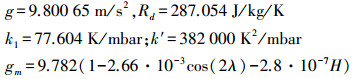全球导航卫星系统(global navigation satellite system,GNSS)卫星信号在通过对流层时产生时延而导致接收机产生的误差称为对流层延迟误差。对流层延迟误差在天顶方向可达2~3 m[1],是北斗等GNSS卫星定位中的重要误差源之一。由于对流层大气分布不均匀,导致对流层延迟误差复杂多样,一般是采用经验模型对其进行改正[2]。总结前人研究成果发现, 这些对流层延迟模型一般分为两类[3]:一是基于理想气体状态方程,针对气象参数建模, 然后利用大气物理方程计算天顶的延迟量,这类模型常用的有Hopfield模型、Saastamoinen模型、Black模型;二是直接对天顶延迟建模,只需要测站的纬度、高程和观测日期相关的经验气象参数,这类模型的代表是EGNOS模型。
本文对上述4种常用模型的建模方法进行了详细的论述,并在Matlab中实现了这些模型的算法。在此基础上,选择了国际GNSS服务(International GNSS Service,IGS)全球观测站中位于中国的6个站(BJFS、WUHN、SHAO、CHAN、URUM和LHAZ),利用全球大地测量观测系统(global geodetic observing system,GGOS) Atmosphere提供的气象数据,用4种模型分别计算得到上述站点2014年的日均对流层天顶延迟数据(zenith tropospheric delays,ZTD),并与IGS组织提供的上述站点2014年的日均ZTD参考值进行了对比验证,然后对4种模型在各站点的精度和误差进行了比对分析和研究。
一、 GNSS信号对流层延迟机理电磁波在真空传播的速度c=299 792.458 km/s,其在真空中沿直线传播,在理想情况下,GNSS信号在大气中的传播距离为
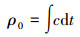 (1)
(1) 若设GNSS信号传播的实际路径为s,传播路径上对流层大气的折射系数为n(s),则其传播速度为
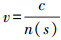 (2)
(2) 因此设信号在大气中的真实传播距离为ρ,则有
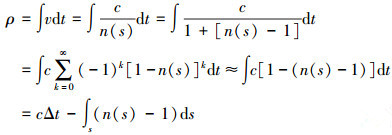 (3)
(3) 式中,Δt是信号在真空中传播ρ所需的时间;ds为传播路径的微元。由式(3)可知,c·Δt为信号源到观测点的几何距离,而在实际观测过程中,因信号在对流层大气中传播速度的变化而产生的折射延迟ΔS可表示为
 (4)
(4) 由于n(s)-1的值很小,因此为了研究和使用方便,又定义了大气折射指数N(s)如下[4]
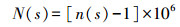 (5)
(5) 式中,N(s)与大气的温度、气压和湿度有关,并且分为干分量Ndry和湿分量Nwet两部分,并且有
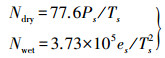 (6)
(6) 式中,Ps为地面大气压,单位为mbar;Ts为地面气温单位为K;es为水汽分压,单位为mbar。
由式(6)可知,只要获取到GNSS信号传播途径上的气象参数,便可计算出相应的大气折射指数,从而计算出对流层的延迟。但是实际上GNSS信号传播路径上的气象参数难以获知,故而只能通过相应的计算模型,利用地面测站的气温Ts、气压Ps和水汽分压es计算传播路径延迟误差。
二、 主要的对流延迟改正模型 1. Hopfield模型1969年H.S. Hopfield利用全球18个台站一年的平均资料,拟合建立了Hopfield模型[5]。Hopfield模型将对流层延迟沿着信号传播方向分为干分量和湿分量,若令i=dry, wet,则对流层延迟总量ΔS为
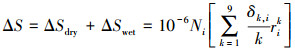 (7)
(7) 式中,折射指数Ndry和Nwet已由式(6)给出;rdry、rwet分别表示地面到信号传播路径干、湿折射指数趋于零的点的距离,单位为m,其计算公式为
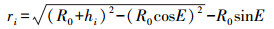 (8)
(8) 其中,hdry和hwet的值定义如下[6]
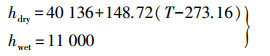 (9)
(9) 对于气温为Ts、气压为Ps、水汽分压为es、高度角为E的测站,经过数值拟合后的Saastamoinen模型的计算公式为[7-8]
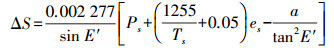 (10)
(10) 式中
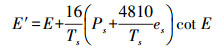 (11)
(11) 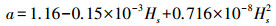 (12)
(12) 式中,Hs表示测站的高程。
3. Black模型H.D.Black于1978年在Hopfield模型的基础上,加入信号传播的路径完全改正后,给出了Black模型,其计算公式为[9]
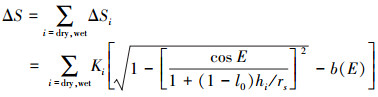 (13)
(13) 其中
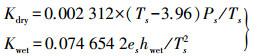 (14)
(14) 式(13)中,rs为测站的地心半径;hwet=1300,hdry=148.98×Ts-3.96;l0和路径弯曲改正因子由下式确定
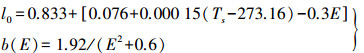 (15)
(15) 上述各式中的温度均采用绝对温度(K),其余参数定义与上述两种模型相同。
4. EGNOS模型EGNOS模型(the European geo-stationary navigation overly system)是欧洲中尺度数值预报中心建立的,与上述几种模型不同的是,在计算对流层天顶延迟时无需输入实测气象数据,而是基于接收机的高程和5个仅与接收机的纬度和年积日有关的气象参数:气压、温度、水汽压、温度梯度和水汽梯度。EGNOS改正模型对流层延迟分为干、湿两个部分[10]
 (16)
(16) 式中,Sdry是干延迟天顶分量(zenith hydrostatic delay);Swet是湿延迟天顶分量(zenith wet delay);m(E)是关于天顶角E的投影函数。将天顶延迟投影到传播路径上,可以简写为
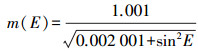 (17)
(17) 干延迟天顶分量Sdry的计算公式为
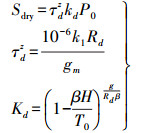 (18)
(18) 湿延迟天顶分量的计算公式为
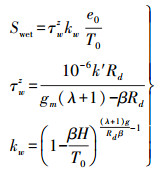 (19)
(19) 其中
式中,气压P0、温度T0、温度变化率β、水汽压e0和水汽变化率λ(无量纲)这5个参数仅与接收机的纬度和年积日有关,可用下式进行插值计算[11]
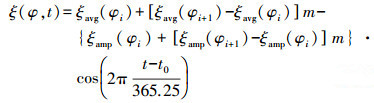 (20)
(20) 式中,φ为测站纬度;t为年积日。
三、 模型比对分析与研究 1. 仿真研究方案为了对模型进行研究和分析,选取了IGS测站中位于中国的6个观测站,这些站点的信息见表 1。
| 观测信息 | 站点 | |||||
| SHAO | WUHN | BJFS | CHAN | URUM | LHAZ | |
| 纬度/φ | 31.10 | 30.53 | 39.51 | 43.79 | 43.47 | 29.66 |
| 高程/m | 22.0 | 40.2 | 87.5 | 273.3 | 917.9 | 3656.6 |
利用GGOS Atmosphere提供的上述6个站点2014年的气象数据,在Matlab中分别用Hopfield、Saastamoinen、Black和EGNOS模型计算上述站点的日均ZTD,并与国际IGS组织通过CDDIS (crustal dynamics data information system)网站提供的2014年的日均ZTD参考值进行对比。同时,为了研究和对比各个模型在各站点的改正精度,分析并给出各个模型相对于各个站点天顶延迟的平均偏差(bias)和表征各个模型计算值的离散程度的均方根误差(RMS)。
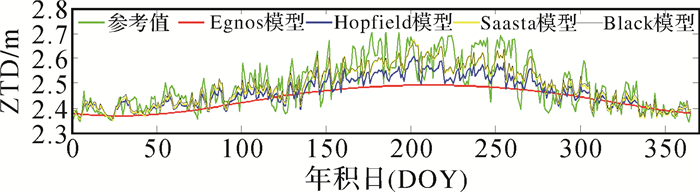
2. 模型验证与对比图 1-图 6分别为4种模型2014年ZTD计算值和IGS提供的ZTD参考值在6个站的延迟日变化的对比。
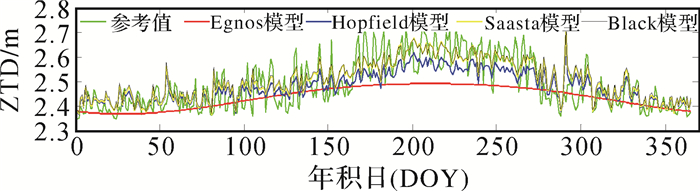
|
| 图 1 4种模型在SHAO站的对比 |
|
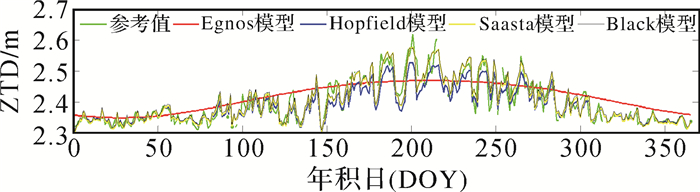
| 图 2 4种模型在WUHN站的对比 |
|
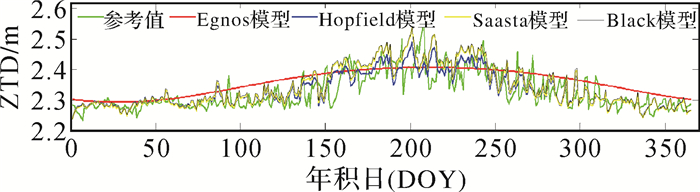
| 图 3 4种模型在BJFS站的对比 |
|
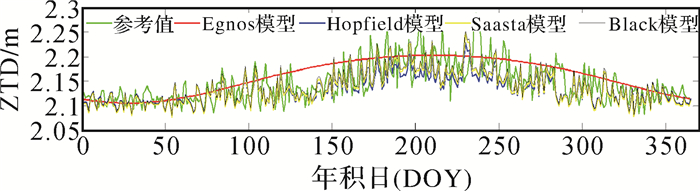
| 图 4 4种模型在CHAN站的对比 |
|
| 图 5 4种模型在URUM站的对比 |
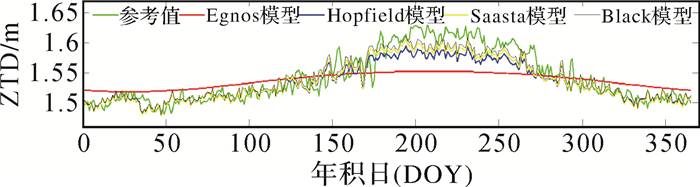
|
| 图 6 4种模型在LHAZ站的对比 |
通过分析发现:
1)从整体上来看,在中国区域的6个测站中,4种模型计算出的ZTD值与IGS给出的参考值基本相符,趋势也基本一致,说明这几种模型都能有效地应用到我国区域的ZTD计算之中。
2)分析ZTD的变化趋势发现,ZTD的值随着季节的变化而发生变化,最大值出现的年积日分别为196(SHAO)、185(WUHN)、191(BJFS)、208(CHAN)、236(URUM)、208(LHAZ),均为夏季;最小值出现的年积日分别为24(SHAO)、364(WUHN)、11(BJFS)、7(CHAN)、338(URUM)、49(LHAZ),均为冬季,可知ZTD夏季最大,冬季最小。并且发现曲线在夏季的波动幅度明显大于冬季,各个模型的计算值与实测值的偏差也是夏季大于冬季,说明各个模型的精度是冬季高于夏季。
3)对比图 4和图 5发现,在纬度相近时,观测站的高程对ZTD的值存在较大影响。其中,CHAN的ZTD取值范围为[2.233, 2.577], URUM的ZTD取值范围为[2.083, 2.288]。对比图 2和图 3发现,在高程相近时,观测站的纬度对ZTD的取值影响不大。其中,BJFS的ZTD取值范围为[2.346, 2.709], WUHN的ZTD取值范围为[2.345, 2.709]。
3. 模型精度分析与对比为分析各个模型在各个站点的改正精度,本文分析并给出各个模型相对于各个站点天顶延迟的平均偏差(bias)和表征各个模型计算值的离散程度的均方根误差(RMS),见表 2。
| 模型 | SHAO | WUHN | BJFS | CHAN | URUM | LHAZ | |||||||||||
| bias | RMS | bias | RMS | bias | RMS | bias | RMS | bias | RMS | bias | RMS | ||||||
| Hopfield | -1.0 | 7.9 | -2.2 | 7.8 | -0.9 | 6.8 | 0.4 | 6.6 | -1.3 | 3.4 | -0.8 | 3.5 | |||||
| Saastamoinen | 1.3 | 6.2 | -0.8 | 6.3 | -0.8 | 5.5 | 1.4 | 5.5 | -1.0 | 2.8 | -0.6 | 3.1 | |||||
| Black | 1.9 | 7.5 | -0.9 | 7.8 | 0.9 | 6.5 | 1.7 | 6.8 | -0.6 | 3.0 | -0.6 | 3.6 | |||||
| EGNOS | 0.5 | 4.3 | -2.9 | 4.4 | 2.0 | 4.3 | 2.8 | 4.1 | 1.0 | 2.8 | -0.3 | 1.2 | |||||
由表 2可知,4种模型在6个观测站的bias的绝对值均小于3 cm,其中最大为EGNOS模型在WUHN站的偏差(-2.9 cm);最小为Saastamoinen模型在LHAZ站的偏差(-0.3 cm)。通过计算可得到4种模型在6个站点的bias绝对值的平均值分别为Hopfield (1.10 cm)、Saastamoinen (0.98 cm)、Black (1.10 cm)、EGNOS (1.63 cm),表明4种模型的精度都比较高,但是整体来说Saastamoinen模型的精度最高,Black模型和Hopfield模型次之,EGNOS模型最低。对于各个站点而言,SHAO站的最适合模型是EGNOS模型,WUHN站、BJFS站和LHAZ站的最适合模型为Saastamoinen模型,CHAN站的最适合模型为Hopfield模型,URUM站的最适合模型为Black模型。由表 2给出的各个站点的RMS信息可知,所有模型的最大误差不超过10 cm。从数据的离散程度来看,EGNOS模型相对于其均值的离散程度最小,Saastamoinen模型次之,Hopfield模型和Black模型离散程度最大,且几乎一致。综上可知,在可以获取实时气象参数的站点建议采用Saastamoinen模型计算ZTD,而在难以获取或缺实时气象参数的站点采用EGNOS模型计算ZTD也可以获得较高的精度。
四、 结论对流层延迟误差是GNSS精确定位中的重要误差源之一,本文基于GGOS Atmosphere提供的2014年的气象数据,利用4种常用的对流层延迟模型计算了我国境内6个测站2014年的ZTD,并将其与国际IGS组织机构CDDIS提供的ZTD数据进行了对比分析,得到以下结论:
1) Hopfield模型、Saastamoinen模型、Black模型和EGNOS模型在我国境内的测站均能使用,并且有较高的精度。
2)对流层天顶总延迟ZTD随着季节的变化而变化,夏季最大,冬季最小;并且4种模型的改正效果也与季节相关,冬季明显优于夏季。
3)几种改正模型的误差均不大于10 cm,而且在需要实时气象参数的模型之中,Saastamoinen模型在中国的6个测站的改正效果要比Hopfield模型和Black模型好。
4)在某些不便实时测定气象参数的应用环境中,EGNOS模型能保证可观的精度,但其精度较Black模型、Hopfield模型和Saastamoinen模型的精度低。
| [1] | 李征航, 黄劲松. GPS测量与数据处理[M]. 2版. 武汉: 武汉大学出版社 ,2010 . |
| [2] | 李昭, 邱卫宁, 邱蕾, 等. 几种对流层延迟改正模型的分析与比较[J]. 测绘通报 , 2009 (7) : 16–18. |
| [3] | 姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报 , 2015, 58 (5) : 1492–1501. |
| [4] | ZHAO T G, MENG W X, ZHANG Z Z.GNSS Signal Tropospheric Zenith Delay Modeling and Analysis[C]//Proceedings of 201113th IEEE Joint International Computer Science and Information Technology Conference.Chongqing:IEEE, 2011. |
| [5] | HOPFIELD H S. Tropospheric Effect on Electron-magnetically Measured Range:Prediction from Surface Weather Data[J]. Radio Science , 1971, 6 (3) : 357–367. DOI:10.1029/RS006i003p00357 |
| [6] | 陈瑞琼, 刘娅, 李孝辉. 卫星导航系统中对流层改正模型分析[J]. 测绘通报 , 2015 (3) : 12–15. |
| [7] | HENRIKSEN S W, MANCINI A, CHOVITZ B H. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging of Satellites[J]. The Use of Artificial Satellites for Geodesy , 2013, 15 (6) : 247–251. |
| [8] | SAASTAMOINEN J. Contribution to the Theory of Atmospheric Refraction[J]. Bulletin Geodesique , 1973 (107) : 13–34. |
| [9] | BLACK H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research:Solid Earth , 1978-2012, 83 (B4) : 1825–1828. DOI:10.1029/JB083iB04p01825 |
| [10] | JIN Shuanggen, ESTEL C, XIE Feiqin. GNSS Remote Sensing:Theory, Methods and Applications[C]//Remote Sensing and Digital Image Processing.[S.L.]:Springer, 2014. |
| [11] | 黄良珂, 刘立龙, 文鸿雁, 等. 亚洲地区EGNOS天顶对流层延迟模型单站修正与精度分析[J]. 测绘学报 , 2014, 43 (8) : 808–817. |
| [12] | 刘靖晔, 宋元明, 胡加星. EGNOS对流层延迟改正模型及其精度分析[J]. 地理空间信息 , 2011, 9 (2) : 96–98. |