天线相位中心是指微波天线的电气中心,其理论设计中心应与天线几何中心一致。但由于天线并非为理想点源,其相位中心将随卫星仰角和方位角而变化[1]。天线相位中心与几何中心之差称为天线相位中心偏差。天线相位中心最大平均偏差可达数厘米[2],若不进行标定和修正,将直接影响测量结果,因此天线相位中心偏差是测量型天线的重要指标。
早期GPS相对测量中,天线相位中心偏差一般认为可以通过差分来消除,但要求使用同一厂商同一型号天线。随着组网规模的增大,混合天线的使用不可避免,逐渐采用平均偏差修正方式来改进相对测量精度。随着GNSS高精度测量技术的进步,应用领域逐步拓展,测量模式已经由较为单一的静态测量发展到包括走走停停、实时或事后动态测量、连续运行参考站(CORS)、实时或事后精密单点定位(PPP)等模式,原来通过差分或平均偏差模型修正来消除天线相位中心偏差的方法也越来越受限制,尤其在动态测量、精密单点定位(PPP)中,天线姿态不断调整,天线相位中心偏差更是难以消除。同时,在GNSS定轨、坐标系统建立与维持、形监测变等毫米级、甚至亚毫米级高精度定位需求的不断牵引下,随着GNSS高精度技术的持续改进,目前不仅要求平均天线相位中心偏差(PCO)小于1 mm,而且还要求对相位中心相对平均相位中心在不同仰角、不同方位的相对变化(PCV)进行标定,标定精度优于0.5 mm[3]。由此可见,现代化GNSS高精度测量对天线相位中心偏差提出了优于1 mm的精度要求。
在GNSS测量型接收机的相关检定规程[4-6]中,对测量型天线相位中心偏差进行了规范,给出了测试方法,并将精度公式中的所谓固定偏差(1倍甚至2倍)作为检测评定门限的依据。笔者认为该门限值的设定不仅理论依据不充分,而且也过于宽松,不利于高精度测量应用。本文将对现有规范的相关内容进行简述,着重分析该检测门限的不合理性,并提出相应的改进建议。
一、 测量型天线相位中心标定方法20世纪90年代早期,天线相位中心大多采用室外天线旋转法进行标定,以平均相位中心的形式进行修正。90年代中后期及以后,为了进一步提高测量精度,逐步采用微波暗室测量法[1]、室外机器人法[7]、室外相对测量法[8]等进行标定,不仅给出了平均相位中心PCO,还以网格模型的形式给出了随仰角和方位角的变化量PCV。美国NGS(National Geodetic Survey)官方网站[9]给出了世界上主流测量型天线厂商多种型号天线的天线相位中心修正模型。目前,国内还没有对测量型天线绝对相位中心进行标定的检测机构,仍采用旋转天线法来标定平均相位中心,并以国家计量技术规范和测绘行业标准的形式对天线相位中心进行了规范。其中文献[4]给出了微波暗室测量法、室外天线旋转法两种方法,而文献[5-6]仅给出了室外天线旋转法一种方法。
技术规范CH 8016-95[4]、JJF 1118-2004[5]、JJF 1347-2012[6]都对室外天线旋转法进行了规范,用相对定位法检定天线相位中心一致性时,在超短基线或短基线上先将GPS接收机、天线按GB/T 18314-2009要求正确安置,按统一约定的方向指向北,观测一个时段。然后固定一个天线,其余天线依次转动90°、180°、270°,各观测一个时段,分别求出各时段基线向量。JJF 1118-2004[5]要求最大值与最小值之差应小于GPS接收机的标称固定标准差;而CH 8016-95[4]、JJF 1347-2012[6]则要求最大互差不能超过2倍固定误差。
比较3个标准,有两点值得注意:一是对于天线相位中心偏差是否合格的判定阈值并不一致,JJF 1118-2004[5]要求最大值与最小值之差应小于GPS接收机的标称固定标准差,而CH 8016-95[4]、JJF 1347-2012[6]要求最大互差不能超过2倍固定误差;二是3个标准都以GPS接收机所谓的“固定标准差”为基准进行判定,姑且不谈3个标准的判定阈值不一致问题,笔者认为以“固定标准差”为基准来判断天线相位中心偏差是否合格,该方法本身就缺乏理论依据,是对测量型接收机精度公式存在误解而导致的错误应用。
二、 测量型接收机精度公式的理解 1. 精度指标公式在GNSS高精度相对测量中,基线测量精度不仅与卫星星历误差、电离层延迟、对流层延迟相关,而且还与卫星几何结构、天线相位中心偏差、多路径效应、观测噪声、数据采样率、数据处理软件及设置、数据处理算法、接收机性能等众多因素相关。
一般而言,由于受卫星星历误差、电离层延迟、对流层延迟等误差影响,基线精度表现为与基线长度相关的线性函数[10]
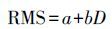 (1)
(1) 式中,a、b为拟合系数,单位分别为mm和mm/km;D为基线长度,单位为km。式(1) 显示基线越长其测量精度越差。由于该精度公式与全站仪精度公式相同,通常采用与全站仪标称精度系数相同的名称,系数a常称为固定误差、固定标准差,b常称为比例系数误差或比例标准差。
不过,如果采用精密星历、双频消电离层组合观测值和对流层估计等技术措施,相对定位精度与基线长度的相关性很小,与观测时段长度密切相关[11-14]。文献[11]基于长度在26~300 km之间的11条基线,将连续观测10天的数据切割为4、6、8、12、24 h等不同时段,利用PAGES专用软件,并采用精密星历、双频载波消电离层等处理方法,获得基线解算,再对其标准差进行拟合,得出GPS基线解相对定位误差(标准差)可以表示为
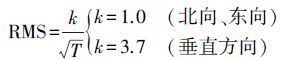 (2)
(2) 式中,T为观测时间,单位为h。式(2) 显示基线精度与基线长度相关性很低,与观测时长直接相关,适用于4~24 h之间的观测时长。文献[12]基于Trimble TTC商用软件,在TTC缺省模式下,分别采用广播星历和精密星历,对10 000多条基线(长度覆盖0.6~1069 km,时长覆盖10 min~24 h)的观测数据进行了处理,给出如下精度拟合公式
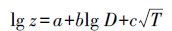 (3)
(3) 式中,D表示基线长度,单位为km;T表示观测时长,单位为h;z表示测量精度,用rms 表示,单位为m;a、b、c为拟合系数。式(3) 显示基线精度与基线长度和观测时间都相关。
由于式(2) 不适用于4 h以下的观测基线,式(3) 复杂不便计算,而式(1) 简易直观,基本上可以反映利用广播星历和商业软件处理的基线精度,因此商业接收机目前仍更多地采用式(1) 来反映接收机的整体测量性能。
由此可见,基线解算精度与众多因素相关,其测量精度也有多种拟合公式。这些公式反映了在不同测量模式、不同处理软件和算法条件下的基线测量精度量级,主要用来指导作业计划和测量实施,也用来反映接收机的整体测量性能。
2. 精度指标公式的理解国际主流的商业测量型接收机大多利用式(1) 来反映接收机在不同测量模式下的测量性能,标称精度(2014年)见表 1。从表中可以看出,在相同测量模式下,不同厂商的接收机系数略有不同;即使是同一型号接收机的不同测量模式,其精度公式系数a、b均有较大差异;水平精度和高程精度的系数也有差异。由此可以看出,a值主要反映了超短基线条件下GNSS星座构型、多路径误差、观测值噪声、天线相位中心等多种因素的综合影响,a值设定的主要目的是为了避免在超短基线情况下对测量精度的预估过于乐观。
| 接收机类型 | 伪距差分 | 长时静态 | 静态/快速精度 | RTK( <30 km) | 网络RTK |
| Trimble R10 | 0.25 m+1×10-6D0.5 m+1×10-6D | 3 mm+0.1×10-6D3.5 mm+0.4×10-6D | 3 mm+0.5×10-6D5 mm+0.5×10-6D | 8 mm+1×10-6D15 mm+1×10-6D | 8 mm+0.5×10-6D15 mm+0.5×10-6D |
| Leica GS14 | 0.25 m | 3 mm+0.1×10-6D3.5 mm+0.4×10-6D | 3 mm+0.5×10-6D5 mm+0.5×10-6D | 8 mm+1×10-6D15 mm+1×10-6D | 8 mm+0.5×10-6D15 mm+0.5×10-6D |
| Novatel | - | - | - | 10 mm+1×10-6D | - |
| Javad RIUMPH-1 | 0.5 m | 3 mm+0.1×10-6D3.5 mm+0.4×10-6D | - | 10 mm+1×10-6D15 mm+1×10-6D | - |
| Ashetch ProMark800 | 0.25 m+1×10-6D | 3 mm+0.1×10-6D3.5 mm+0.4×10-6D | 3 mm+0.5×10-6D5 mm+0.5×10-6D | 10 mm+1×10-6D20 mm+1×10-6D | - |
将a理解为仪器固定误差,认为它仅包含接收机天线相位中心偏差,并以此为依据来限定天线相位中心偏差的检测门限,不但缺乏理论依据,而且该门限也过于宽松,不利于高精度测量应用。表 1中a值最小为3 mm。表中同一型号接收机,a值一般约5 mm。如果将5 mm作为天线相位中心偏差的检测门限,而天线相位中心偏差的确也存在5 mm偏差却又通过了检测,这将会给后续GNSS测量引入无法解决的偏差。因为天线相位中心偏差只有通过精确标定才能解决,难以通过数据处理来解决。5 mm偏差对于很多毫米级甚至亚毫米级精度的测量应用是不可接受的,如大地坐标系的建立与维护、形变监测、水准测量、精密工程测量等。
4. 天线相位中心偏差有可独立检测的指标要求测量型天线相位中心偏差有独立的指标要求,如Trimble Zephyr Geodetic 2天线相位中心偏差最大不大于2 mm[9]。标定方法包括天线旋转法、微波暗室标定法、机器人野外标定法等,天线标定精度优于0.5 mm[2-3, 9]。
三、 结论1) 国内GNSS测量型接收机的检定规程中,天线相位中心采用室外天线旋转法进行标定,并以GNSS测量型接收机标称精度中所谓的“固定标准差”作为阈值进行判定。该阈值的设定缺乏理论依据,是对测量接收机精度公式存在误解而导致的错误应用,存在给GNSS测量引入无法解决的偏差的隐患。
2) GNSS测量型接收机标称精度中的a值,与星历类型、数据处理软件、观测时间长度、天线相位中心偏差等因素相关,其主要目的是为了避免在超短基线情况下对测量精度的预估过于乐观。
3) 天线相位中心偏差有独立的指标要求,也有独立的精确检测方法,因此建议按照天线相位中心偏差的指标要求设定检测门限,而不要采用精度公式中的a值作为检测门限。
| [1] | BARTELS G A. GPS-Antenna Phase Center Measurements Performed in an Anechoic Chamber[M]. Delft: Delft University Press , 1997 : 8 -12. |
| [2] | SCHUPLER B R, CLARK T A. Characterizing the Behavior of Geodetic GPS Antennas[J]. GPS World , 2001, 12 (2) : 48–55. |
| [3] | GÖRRES B, CAMPBELL J, BECKER M, et al. Absolute Calibration of GPS Antennas: Laboratory Results and Comparison with Field and Robot Techniques[J]. GPS Solution , 2006 (10) : 136–145. |
| [4] | 全球定位系统(GPS)测量型接收机检定规程: CH 8016-1995[S]. 北京: 测绘出版社, 1995. |
| [5] | 全球定位系统(GPS)接收机(测地型和导航型)校准规范:JJF 1118-2004[S].北京: 中国计量出版社, 2004. |
| [6] | 全球定位系统(GPS)接收机(测地型)型式评价大纲: JJF 1347-2012[S].北京: 中国计量出版社, 2012. |
| [7] | WÜBBENA G, SCHMITZ M, MENGE F, et al. Automated Absolute Field Calibration of GPS Antennas in Real Time[C]//Proceedings of ION GPS 2000. Salt Lake City:[s.n.], 2000. |
| [8] | MADER G L. GPS Antenna Calibration at the National Geodetic Survey[J]. GPS Solutions , 1999 (3) : 50–58. |
| [9] | BILICH A, MADER G L. GNSS Absolute Antenna Calibration at the National Geodetic Survey[C]//The 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland:[s.n.], 2010. |
| [10] | BEUTLER G, BAUERSIMA I, BOTTON S, et al. Accuracy and Biases in the Geodetic Application of the Global Positioning System[J]. Manuscripta Geodaetica , 1989 (14) : 28–35. |
| [11] | ECKL M C, SNAY R, SOLER T, et al. Accuracy of GPS-derived Relative Positions as a Function of Interstation Distance and Observing-session Duration[J]. Journal of Geodesy , 2001, 75 (12) : 633–640. DOI:10.1007/s001900100204 |
| [12] | HÄKLI P, KOIVULA H, PUUPPONEN J. Assessment of Practical 3-D Geodetic Accuracy for Static GPS Surveying[C]//Integrating Generations FIG Working Week 2008 Stockholm. Sweden:[s.n.], 2008. |
| [13] | SNAY R A, SOLER T, ECKL M. GPS Precision with Carrier Phase Observations: Does Distance and/or Time Matter?[J]. Professional Surveyor Magazine , 2002, 22 (10) : 20, 22, 24. |
| [14] | SOLER T, MICHALAK P, WESTON N D, et al. Accuracy of OPUS Solutions for 1-to 4-h Observing Sessions[J]. GPS Solution , 2006 (10) : 45–55. |


