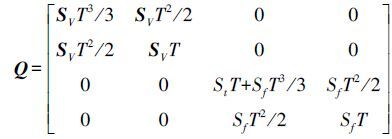北斗卫星导航系统(Beidou Navigation Satellite System,BDS)是中国正在实施的自主发展、独立运行的全球卫星导航系统[1]。截至2015年7月,北斗系统在轨工作卫星为13颗,形成区域服务能力,面向我国及周边部分地区提供无源定位、导航和授时等服务。北斗伪距单点定位具有速度快、数据处理简单等优点,其定位精度为10 m[1],是导航与低精度测量中常用的一种定位方法。常见的伪距单点定位算法有高斯牛顿迭代最小二乘(Gauss-Newton isterative least squares, GNILS)定位算法,加权最小二乘(weighted least squares, WLS)快速算法[2]。通过前人的研究,北斗伪距单点定位平面精度优于3.5 m,高程精度优于8 m[3]。
卡尔曼滤波作为一种降低、分离卫星信号中所含有噪声量的技术,可以用来提高北斗伪距单点定位的精度。由于最小二乘法没有将不同时刻的定位值联系起来相互制约,使得其定位结果通常会显得非常粗糙。所谓滤波,就是将一个信号中的某些成分过滤掉,并保留所需要的信号成分。所有滤波的一个共同特点是将用户在相邻时刻的位置状态联系起来,从而克服最小二乘法在不同时刻的定位值之间不互相关联的这一缺点,使滤波后的定位结果显得更加平滑、准确。卡尔曼滤波技术是一种线性最小方差滤波估计,它只需要通过上一时刻状态向量的最优估计和现在时刻的观测值就可以得到当前时刻状态向量的最优估计值[4-6]。
本文通过建立单点定位和卡尔曼滤波数学模型,对采集的数据分别进行最小二乘伪距单点定位解算和卡尔曼滤波解算,得出各自的处理结果,并比较分析两者的区别,得出相应的结论。
一、 数学模型 1. 伪距单点定位原理伪距测量的观测方程可表示为[7]
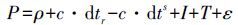 (1)
(1) 式中,P为伪距观测值;ρ为卫星与接收机之间的真正距离;c为光速;dtr和dts分别为接收机钟和卫星钟差;I为电离层延迟改正;T为对流层延迟改正;ε表示伪距的观测噪声和多路径延迟的影响。
线性化后式(1) 可表示为
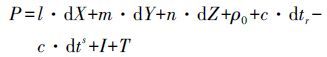 (2)
(2) 式中,(l, m, n)为接收机到卫星的方向余弦;ρ0为测站到卫星的距离初值;(dX, dY, dZ)为测站坐标的改正数。利用伪距观测方程进行最小二乘平差即可求出测站坐标和接收机钟差。
2. 多普勒单点测速原理由于接收机和卫星的相对运动,造成传播路程差,导致相位和频率的变化,这种变化称为多普勒频移[8]。通过多普勒频移可以求出接收机的速度。
观测方程可以从伪距观测方程推导出来,式(2) 对时间进行微分可得
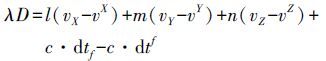 (3)
(3) 式中,λ为载波相位的波长;D为卫星的多普勒观测值;(vX, vY, vZ)表示接收机的运动速度;(vX, vY, vZ)表示卫星的运动速度;dtf和dtf分别表示接收机和卫星钟差的变化率。利用多普勒观测方程进行最小二乘平差即可求出接收机的速度和钟速。
3. 卡尔曼滤波原理随着对卡尔曼滤波器的深入研究,卡尔曼滤波技术已被运用于求解GPS位置、速度和时间,在北斗伪距单点定位中仍然适用。假设接收机低速运动,则其运动状态可采用常速模型(历元间接收机速度不变)表示为
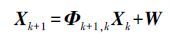 (4)
(4) 式中,下角标k表示历元号;X为描述接收机运动状态的向量;Φ为前后历元的状态转移矩阵;W表示过程噪声向量。假设T为采样间隔,则有
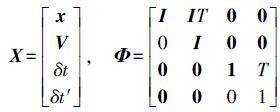 (5)
(5) 式中,x=xyzT为接收机的位置分量;V=vXvYvZT,为接收机的速度分量;δt和δt′分别为接收机钟差和频漂;I为一个3×3的单位阵。
联合伪距和多普勒的观测方程,即可得到系统的观测方程为
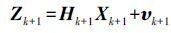 (6)
(6) 式中,
为观测值向量,分别由伪距和多普勒观测值组成;Hk+1代表观测量与系统状态之间的关系矩阵,且有
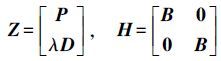 (7)
(7) 结合式(4) 和式(6) 即可组成卡尔曼滤波系统,然后按照卡尔曼滤波的递推公式即可依次求出每个历元的状态向量及其协方差阵。本文滤波过程噪声W的方差矩阵定义为
观测噪声的方差矩阵R[7]定义为
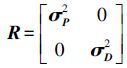 (9)
(9) 式中,
SV=diag(SVX, SVY, SVZ)为速度噪声,是加速度的功率谱密度值,其中diag()表示对角阵;(St, Sf)为钟差噪声和钟漂噪声的功率谱密度,经过调试,(SVX, SVY, SVZ)、(St, Sf)均取0.05可获得较好结果。σP2=diag(σP12,σP22,…,σPk2),为伪距观测值的观测方差阵;σD2=diag(σD12,σD22,…,σDk2),为多普勒测值的观测方差阵;σP2、σD2均为k×k的对角阵,由于多普勒观测噪声远小于伪距观测噪声,且其具体数值很难获取,故先验给出,经过调试,取σ2Pi=4.5、σDi2=0.18时的滤波结果较好。
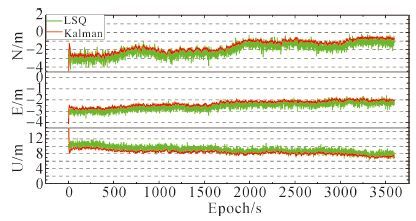
二、 算例分析 1. 静态数据分析静态数据采用2015年1月16日武汉大学教学实验大楼楼顶的观测数据,接收机为Trimble NetR9,采样率为1 Hz,采样时间为8:00—9:00(GPS时)。对于伪距单点定位,对流层延迟改正采用简化的Hopfield模型[9],电离层延迟改正采用Klobuchar模型[10]。平差过程采用标准最小二乘和卡尔曼滤波两种处理方式,其定位结果与事先已知的测站精确坐标进行对比,并将三维坐标偏差转换到站心坐标系,得到两种解算模式下的定位结果在N、E、U方向上的偏差,如图 1所示。
|
| 图 1 两种定位结果的精度比较 |
从图 1可以看出,在滤波初始阶段偏差很大,但是经过10多个历元后趋于稳定,出现这种现象是因为给定的滤波初始值不准确,且用的是动态滤波模型处理静态数据,因此会有一个滤波收敛的过程;经过对比,卡尔曼滤波的处理结果明显比最小二乘估计平滑,波动幅度更小,更加趋近于实际,精度更高,可靠性更好。通过两种处理方式获得的定位结果与已知的测站精确坐标,计算出各自的均方根误差(RMS值)见表 1。
表 1的数据可以反映出卡尔曼滤波解算的定位结果比最小二乘解算结果更优,在平面方向上的精度提高42%,高程方向提高22%。但是,从偏差的大小来看,卡尔曼滤波的结果仍存在一定偏差,其原因在于所采用的定位数据为静态数据,而本文所建立的滤波器模型为低动态滤波模型,与实际情况存在一定偏差,从而导致滤波估值未能达到最优。
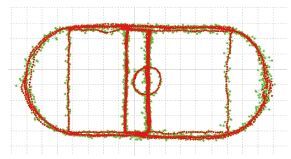
2. 动态数据分析动态数据采用2015年1月16日在武汉大学信息学部操场绕行的观测数据,接收机为Trimble NetR9,采样率为1 Hz,采样时间为8:00—9:00(GPS时)。围绕学校操场走圈而获得接收机的运动轨迹,所采用的数学模型与静态数据所采用的模型一致,经过数据处理,得到最小二乘与卡尔曼滤波的解算结果。两种方法得到的轨迹如图 2和图 3所示,其中灰色为最小二乘解,深灰色为卡尔曼滤波解。表 2是通过GrafNav精密软件处理得到的操场运动轨迹的参考坐标,分别与最小二乘和卡尔曼滤波解算结果定量进行对比分析,计算出各自的RMS值。
|
| 图 2 轨迹全局 |
|
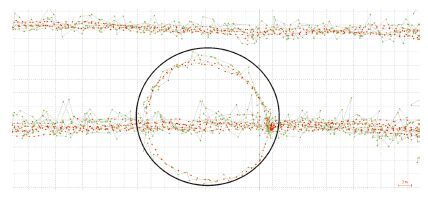
| 图 3 操场中间圆圈细节 |
根据伪距观测值解算出的接收机轨迹如图 2所示,经过数据处理,卡尔曼滤波的定位轨迹相比最小二乘解的定位轨迹更加平滑、集聚,定位偏差更小、可靠性更高。为了更好地证明以上结论,特取信息学部操场中间的圆圈轨道细节图,如图 3所示,卡尔曼滤波解较最小二乘解轨迹偏差更小,波动幅度小,各个点位之间更加连续,更加趋近于实际运动轨迹,定位结果更好。从表 2也可以看出,卡尔曼滤波定位结果在平面方向精度提高33%,高程方向提高21%。总的来说,相对于最小二乘解算结果,经卡尔曼滤波处理后可获得更好的结果。
通过分析卡尔曼滤波对静态数据和动态数据的处理结果,得出以下结论:
1) 该滤波模型对于静态数据和动态数据的处理,一定程度达到了平滑和提高精度的作用。从对静态数据的处理结果来看,由于模型误差及给定的滤波初值不够准确,导致滤波初始阶段存在很大偏差,经过一段历元之后回归正常,但相比最小二乘解算结果来说,卡尔曼滤波解算结果精度更高,更平滑,平面及高程方向的可靠性均有所提高。从对动态数据的处理结果分析可知,卡尔曼滤波解算结果较最小二乘解算结果轨迹偏差更小,波动幅度小,各个点位之间更加连续,过渡更自然,更加趋近于实际运动轨迹,定位结果更优。
2) 与最小二乘结果相比,使用卡尔曼滤波算法对观测数据进行处理的精度和可靠性都更高,结果更加平滑,对于实际应用具有一定的参考意义。
本文对获取的动态数据和静态数据的卡尔曼滤波分别进行处理与分析,最后得出结论:卡尔曼滤波估计对最小二乘结果具有平滑和提高精度的作用,对于实际应用来说具有一定的参考价值。
| [1] | 陈坡, 孙付平, 韩雪峰, 等. 北斗卫星导航系统定位精度分析[J]. 海洋测绘 , 2013, 33 (5) : 34–37. |
| [2] | 李春华, 蔡成林, 邓克群, 等. 一种北斗伪距单点定位的加权最小二乘(WLS)快速算法[J]. 重庆邮电大学学报(自然科学版) , 2014, 26 (4) : 466–472. |
| [3] | 陆亚峰, 蒋海林, 彭遥. 北斗伪距单点定位与差分定位结果精度分析[J]. 海洋测绘 , 2014, 34 (4) : 28–30. |
| [4] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社 ,2009 : 127 -135. |
| [5] | 杨丹. 卡尔曼滤波器设计及其应用研究[D]. 湘潭:湘潭大学, 2014. http://cdmd.cnki.com.cn/article/cdmd-10530-1014412541.htm |
| [6] | 赵奇. 卡尔曼滤波在GPS定位中的研究与实现[D].成都:电子科技大学, 2013. |
| [7] | 刘威, 陈向东, 朱军, 等. 北斗单频与多频伪距单点定位精度与可用性分析[C]//第五届中国卫星导航学术年会论文集.北京:[s.n.], 2014. |
| [8] | 单瑞, 赵铁虎, 于得水, 等. 单点GPS多普勒测速模型比较与精度分析[J]. 测绘通报 , 2013 (3) : 7–9. |
| [9] | 唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J]. 武汉大学学报(信息科学版) , 2015, 40 (4) : 529–533. |
| [10] | 李征航, 黄劲松.GPS测量与数据处理[M]. 2版. 武汉:武汉大学出版社, 2010:97-99. |
| [11] | YAMAGUCHI S, TANAKA T. GPS Standard Positioning Using Kalman Filter[C]//International Joint Conference on SICE-ICASE.[S.l.]:IEEE, 2006: 1351-1354. |
| [12] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估 , 2014, 44 (1) : 72–81. |