2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
合成孔径雷达(SAR)为侧视斜距成像,地形起伏会对SAR影像造成较大的几何畸变[1],存在着不同程度的透视收缩、叠掩和阴影等现象,在横断山脉等复杂地形区域表现得尤为突出[2],从而大大限制了其应用范围。因此,从SAR影像上获取地物特征的精确空间位置信息,或对多时相、多源信息进行综合分析,需要对SAR影像进行高精度的正射纠正。
星载SAR影像的正射纠正是利用几何模型、数字高程模型(digital elevation model,DEM)及控制点,将星载SAR影像的SLC产品按照指定采样间隔重投影到指定坐标系。目前,针对星载SAR影像的几何模型,很多学者进行了相关研究。侯家槐等利用距离多普勒模型进行星载SAR影像正射纠正,TerraSAR-X影像在稀少控制点纠正后最高可以达到5.21 m的精度[3];张波等针对Radarsat-1影像,采用距离多普勒模型与共线方程分别进行星载SAR影像的正射纠正,利用同一地区获取的高精度控制点和数字高程模型对两种方法进行系统分析比较,两个模型的精度输出基本一致[4];Zhang G等采用有理函数模型(Rational function model, RFM)拟合SAR影像的成像几何模型,对TerraSAR-X、COSMO-SkyMed、ERS-2和ENVISAT ASAR影像进行正射纠正,在平原地区可达2 m的精度,在高山地区可达7 m的精度[5]。
在以上相关研究中,均需要利用地面控制点来消除轨道和距离测量引起的系统误差,控制点的像点坐标量测精度直接影响SAR影像的定向精度[6],进而影响正射纠正精度。由于角反射器点在SAR影像中呈现为“亮点”,容易精确提取角反射器点的像面坐标,故通过角反射器点进行SAR影像的正射纠正是一种常见的方法。然而,布设角反射器是一项很艰巨的任务,无法满足SAR正射影像的大区域生产和工程化需求,在某种程度上限制了其广泛应用。因此,需要通过在星载SAR影像和相关正射影像上选取控制点,优化几何模型参数进行正射纠正,减少布设角反射器成本,提高工程化应用的可能性。
资源三号测绘卫星是我国第一颗民用高分辨率测绘卫星[7],与国外相近分辨率的卫星相比,可以达到较高的几何精度,在四角布设控制点的情况下DOM平面精度优于3 m,DSM高程精度优于2 m[8-9]。本文利用资源三号卫星影像的DSM和DOM,在RFM的基础上采用四角布设控制点的方式,选取遥感13号SAR卫星影像与资源三号光学影像的同名点作为控制点,对遥感13号SAR影像进行正射纠正,并与基于角反射器点的正射纠正方法进行对比分析。
一、 基于RFM的星载SAR正射纠正 1. 基于RFM的星载SAR几何模型RFM能获得与严密成像几何模型近似相同的精度,但形式更简单[10]。为了减少计算过程中由于数据数量级差别过大引入的舍入误差,增强参数求解的稳定性,RFM将地面坐标和影像坐标标准化到-1到1之间。对于一个遥感影像,定义如下比值多项式[11]
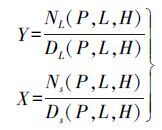 (1)
(1) 式中,NL(P, L, H)、DL(P, L, H)、Ns(P, L, H)、Ds(P, L, H)为P、L、H的三次多项式;(P, L, H)为正则化的地面坐标;(X, Y)为正则化的影像坐标。
由于卫星星历、传感器延时和测距等观测值常常带有误差,根据这些参数建立的针对星载SAR的严密几何模型不可避免地包含误差,故利用带有误差的距离多普勒模型求解RFM参数会带有误差,进而对SAR影像的几何精度存在行方向误差与列方向误差。在RFM的基础上,通过建立影像面上的仿射变换模型来消除这两类误差。仿射变换定义为
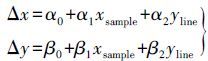 (2)
(2) 式中,Δx、Δy为控制点在影像坐标系中量测坐标与真实坐标的差值;xsample、yline为地面控制点利用RFM投影至影像面的像面坐标值;α0、α1、α2、β0、β1、β2为影像对应的平差参数。
2. 星载SAR正射纠正根据DEM坐标空间与SAR影像坐标空间的映射关系式(1) 和式(2) 建立了DEM和真实SAR影像之间的几何关系,采用间接纠正方式,即利用双线性内插获得正射影像的灰度值,从而获得正射纠正后的影像。主要步骤如下:
1) 解算模型参数。由距离多普勒模型构建的星载SAR严密成像几何模型,建立空间格网,采用与地形无关的RFM参数求解方式,求解RFM参数;根据式(1) 和式(2) 构建的优化星载SAR几何模型,利用4个以上的地面控制点求解6个平差参数。
2) 计算地面点坐标。设正射影像上任意一点P的像面坐标为P(xi, yi),根据式(1) 和式(2) 的正变换,计算出P点对应的地面坐标PX, Y, Z。
3) 计算像面点坐标。根据式(1) 和式(2) 的反变换,计算出P点在原始影像中的像面坐标P′x′, y′。
4) 灰度值内插。由于P′点像面坐标不一定为像素中心,采用双线性内插获得P′点的灰度值g′x′, y′。
5) 生成正射影像。将原始影像中P′点的灰度值g′x′, y′赋给正射影像的P点,获得正射影像。
3. 控制点选取针对平原和丘陵等选点较容易区域的星载SAR影像,通常在SAR影像上选取控制点,优化星载SAR几何模型参数进行正射纠正。控制点的选取可以分为两类:一是基于布设的人工角反射器点选取控制点;二是基于光学正射影像选取控制点。
(1) 基于角反射器点的选取
角反射器点的识别主要有两种方法,即目视识别和算法提取[12]。由于SAR影像斑点噪声的存在,目视识别无法准确找出角反射器点的准确位置;定位模型的误差导致算法提取角反射器点可能存在偏差。因此,本文采用目视识别和算法提取相结合的方法确定角反射器点的准确位置。
首先,根据角反射器点的地面坐标和SAR影像的成像几何模型,预测角反射器点在SAR影像的大致位置;然后,通过目视识别的方法,人工初步确定角反射器点在SAR影像上的中心位置;最后,利用亚像元精度的算法[13],即根据目标像点的灰度分布特性,通过内插细分算法精确提取角反射器点的像点坐标,提取精度可达1/16像素。
(2) 基于光学正射影像的选取
以资源三号卫星正射纠正影像产品等为参考影像,选取星载SAR影像和光学影像的同名像点作为星载SAR影像正射纠正的控制点。李莹莹等提出了一种基于归一化互相关原理的高分辨率SAR 图像与光学图像之间的同名点精匹配方法[14],但该方法需要先进行人工选取少量控制点。通常情况,采用四角布设控制点即可进行星载SAR正射纠正。因此,本文采用人工选取控制点的方式进行星载SAR正射纠正。
由于光学影像和SAR影像的成像机理和影像纹理不同,故同名像点(即控制点)的选取是非常困难的。根据选点经验,得出以下几个选取光学影像和SAR影像同名像点的原则:①选择道路的“十”字交叉口或“T”字交叉口,确定两条道路中心线的交点。由于SAR影像的道路纹理较清晰,便于与光学影像的道路进行匹配,而且道路一般地势平坦,因而受高差影响较小。②道路尺寸适当,道路过窄在SAR影像上无法清晰识别,道路过宽则无法确定中心线的准确位置。③由于斑点噪声的存在,SAR影像的道路边界没有光学影像的清晰,尤其是两条路的交汇处,故应尽量选择两条笔直的道路,根据两条路的趋势走向来确定两条道路中心线的交点。④两条道路交叉处起伏或高差应尽量小,如避免选择天桥处的“十”字交叉口。⑤道路周围地势平坦,防止地物或建筑物对道路成像造成影响,如避免道路“十”字交叉口附近有房屋等。
根据以上的选点原则,选取了西安市阎良区遥感13号影像和资源三号影像的同名点,如图 1所示。其中,左侧为遥感13号影像,右侧为资源三号影像。

|
| 图 1 遥感13号和资源三号同名点选取 |
本文将地势较平坦的陕西省西安市阎良区和渭南市蒲城县两个地区作为试验区,获取了资源三号三线阵影像数据与统一的地面控制点数据,对遥感13号SAR卫星影像进行正射纠正试验。
1. 试验数据试验采用的资源三号三线阵影像数据,成像时间为2014年5月8日,分辨率分别为3.5、2.5、3.5 m;两景遥感13号SAR影像数据,成像时间是2014年7月16日,分辨率为3 m,阎良地区影像为降轨右视,蒲城地区影像为升轨右视。
利用双频GPS接收机,采集了37个厘米级精度的野外测量控制点数据。其中,光学控制点18个,角反射器点19个,大部分光学控制点和角反射器点都存在一一对应关系,每组点相距100 m左右,其中点号为5210的角反射器点无对应的光学控制点。影像数据和控制点分布如图 2所示。
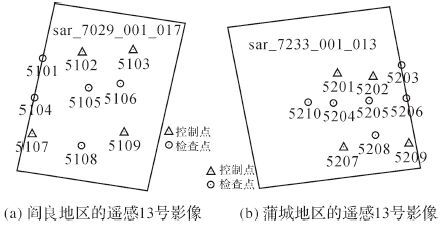
|
| 图 2 影像与控制点的分布 |
由于遥感13号SAR卫星的波位限制,部分角反射器点未成像到相应的SAR影像范围内,点号分别为5101、5104、5203。
2. 试验方法本次试验采用以下两种方案:
方案1:以角反射器点作为控制点的正射纠正方法。采用四点布控的方法,基于RFM对资源三号三线阵影像数据进行立体平差,利用资源三号前、后视影像构建立体像对制作高精度的DSM。根据角反射器点的像面坐标和地面坐标,采用四角布控的方法求解仿射变换参数,分别对阎良地区和蒲城地区的遥感13号SAR影像进行正射纠正。
方案2:基于资源三号卫星影像选取控制点的正射纠正方法。首先,利用方案1制作的高精度DSM,对资源三号正视影像进行正射纠正。利用星载SAR影像和分辨率相匹配的光学影像,通过在SAR影像的四角区域寻找同名像点作为控制点,根据资源三号的DSM和DOM提取控制点的地面坐标,求解仿射变换参数,结合资源三号高精度DSM分别对阎良和蒲城地区的遥感13号SAR影像进行正射纠正。
本次试验均以野外采集的角反射器点作为检查点,对两种方案的SAR正射影像精度进行评价。
3. 试验结果及分析(1) 资源三号定位精度
① 高程精度验证
利用野外测量的光学控制点和角反射器点的GPS高程值,与资源三号DSM相应内插出的高程值进行差值计算,对所提取的DSM进行精度验证,它能直接反映资源三号立体影像获取的DSM精度。经统计,高程中误差为1.504 m。
② 平面精度验证
选取一定数量的控制点,控制点在正射影像上的平面坐标与该控制点的实测坐标之间存在一个差值,统计所有控制点的精度即为正射影像的纠正精度。资源三号影像的正射纠正精度见表 1。
| m | |||
| ID | 差值 | ||
| ΔX | ΔY | 平面 | |
| 101 | 0.687 5 | -4.657 1 | 4.707 6 |
| 102 | 1.339 5 | -3.740 1 | 3.972 7 |
| 103 | -0.203 5 | -3.669 1 | 3.674 7 |
| 104 | 1.904 5 | -4.181 1 | 4.594 4 |
| 105 | 1.746 5 | -3.843 1 | 4.221 3 |
| 106 | 0.602 5 | -2.194 1 | 2.275 3 |
| 108 | 1.061 5 | -3.047 1 | 3.226 7 |
| 202 | 0.103 5 | -2.321 1 | 2.323 4 |
| 204 | 2.047 5 | -2.212 1 | 3.014 2 |
| 205 | 0.679 5 | -2.862 1 | 2.941 7 |
| 206 | 0.123 5 | -2.207 1 | 2.210 6 |
| 207 | 1.801 5 | -1.424 1 | 2.296 4 |
| 208 | 1.213 5 | -2.538 1 | 2.813 3 |
| 209 | 2.8745 | -3.241 1 | 4.332 1 |
| 误差均值 | 1.417 6 | 3.1374 | 3.442 8 |
从表 1的结果可以看出,该地区的资源三号正射影像平面定位精度在3 m左右。综合资源三号DSM的高程精度,可以说明基于资源三号影像选取星载SAR影像控制点的可靠性。
(2) 遥感13号正射纠正
① 影像定向试验
采用方案1和方案2,分别对阎良地区和蒲城地区的遥感13号SAR影像进行单景定向试验,结果见表 2和表 3。
| pixels | ||||||||
| 方案 | 控制点个数 | 检查点个数 | 控制点精度 | 检查点精度 | ||||
| x | y | 平面 | x | y | 平面 | |||
| 方案1 | 4 | 3 | 0.028 | 0.302 | 0.303 | 0.44 | 0.709 | 0.834 |
| 7 | 0 | 0.277 | 0.415 | 0.5 | — | — | — | |
| 方案2 | 4 | 7 | 0.535 | 0.55 | 0.768 | 1.142 | 1.214 | 1.667 |
| 11 | 0 | 0.672 | 0.711 | 0.978 | — | — | — | |
| pixels | ||||||||
| 方案 | 控制点个数 | 检查点个数 | 控制点精度 | 检查点精度 | ||||
| x | y | 平面 | x | y | 平面 | |||
| 方案1 | 4 | 5 | 0.054 | 0.07 | 0.088 | 0.353 | 0.413 | 0.543 |
| 9 | 0 | 0.171 | 0.242 | 0.296 | — | — | — | |
| 方案2 | 4 | 9 | 0.035 | 0.287 | 0.289 | 1.438 | 0.591 | 1.555 |
| 13 | 0 | 0.72 | 0.375 | 0.812 | — | — | — | |
通过以上试验结果可以看出,通过四角布控的方式,两种方案的定向精度大幅度提升,分别优于0.9和1.7像素,说明很好地消除了各景影像存在的系统误差。相比之下,方案1比方案2的单景定向精度高,从全部控制点的定向结果可以看出,方案2可能存在一定的选点误差。
② 正射纠正
采用两种方案对阎良和蒲城两个地区的遥感13号SAR影像进行正射纠正,精度见表 4和表 5。
| m | ||||||
| ID | 方案1差值 | 方案2差值 | ||||
| ΔX | ΔY | 平面 | ΔX | ΔY | 平面 | |
| 5102 | — | — | — | -3.419 | -1.9 | 3.911 |
| 5103 | — | — | — | 2.817 | -5.532 | 6.208 |
| 5105 | -2.914 | 0.627 | 2.98 | -1.572 | 3.205 | 3.57 |
| 5106 | -0.865 | 0.012 | 0.865 | -1.823 | -4.21 | 4.588 |
| 5107 | — | — | — | 3.988 | 2.472 | 4.692 |
| 5108 | -2.49 | 0.502 | 2.5396 | -1.148 | 3.08 | 3.287 |
| 5109 | — | — | — | 3.746 | -4.015 | 5.491 |
| 误差均值 | 2.268 | 0.464 | 2.315 | 2.53 | 3.646 | 4.502 |
| m | ||||||
| ID | 方案1差值 | 方案2差值 | ||||
| ΔX | ΔY | 平面 | ΔX | ΔY | 平面 | |
| 5202 | — | — | — | 2.089 | 4.313 | 4.792 |
| 5204 | 2.549 | 2.233 | 3.389 | -2.878 | 2.232 | 3.642 |
| 5205 | 1.965 | 1.321 | 2.368 | -1.262 | 3.3197 | 3.552 |
| 5206 | 2.326 | 0.004 | 2.326 | 3.499 | 2.003 | 4.032 |
| 5207 | — | — | — | -3.502 | -1.972 | 4.019 |
| 5208 | 1.551 | 0.761 | 1.728 | -1.676 | 2.76 | 3.229 |
| 5209 | — | — | — | -2.185 | -2.207 | 3.106 |
| 5210 | 2.304 | 0.115 | 2.307 | -3.123 | -1.886 | 3.648 |
| 误差均值 | 2.167 | 1.211 | 2.482 | 2.577 | 2.707 | 3.742 |
通过以上结果可以看出,两种方案的正射纠正精度与单景定向精度基本一致。方案1的正射纠正精度优于2.5 m,方案2的正射纠正精度优于4.5 m;根据单景定向结果可以看出,由于方案2相比之下存在一定的选点误差,方案1比方案2的正射纠正精度高。但是,方案2的正射纠正精度仍可以满足1∶1万测图需求。由此可以说明,利用资源三号的高精度DSM和DOM,选取遥感13号SAR影像与资源三号光学影像的同名像点作为控制点,对平原地区的遥感13号SAR影像进行正射纠正的方法是可行的。
(3) 误差分析
由于星载SAR是斜距成像,地形起伏引起正射纠正的误差是主要的误差源。本文采用资源三号的高精度DSM产品作为高程参考,因此DSM的误差是正射纠正试验的主要理论误差。
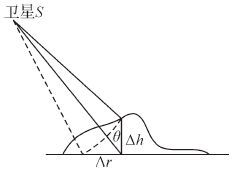
如图 3所示,地面高程误差Δh引起的定位误差为
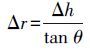 (3)
(3) 式中,Δh为地表高程误差;θ为雷达入射角;Δr为由于高程误差在斜距方向引起的误差,即定位误差。
由上可知,试验区的资源三号DSM高程精度为1.50 m,可根据拍摄计划的雷达入射角,估计SAR影像的高程误差引起的定位误差,结果见表 6。
由于定向精度分别为1.67和1.56像素,正射纠正影像的理论平均精度应分别在2.41~7.61 m和3.16~6.20 m之间,由表 4和表 5的结果可以看出,此次试验的正射纠正结果是合理的。
三、 结论在RFM模型的基础上,利用国产星载SAR影像与分辨率相匹配的光学影像选取同名像点作为控制点,对西安市阎良地区和渭南市蒲城县两个地区的遥感13号SAR影像进行正射纠正,与基于角反射器点的正射纠正方法进行对比分析,得到如下结论:
1) 在四角布控的情况下,平原地区的资源三号卫星影像可以提供高精度的DSM和DOM产品,平面精度约3 m,高程精度优于2 m。
2) 针对平原地区的遥感13号SAR影像,基于光学正射影像的正射纠正方法比基于角反射器点的正射纠正方法精度略差,但平面精度优于4.5 m,可以满足1∶1万测图的需求。
3) 提出星载光学影像和星载SAR影像同名像点的选取准则,确保了星载SAR影像的定向精度和正射纠正精度。
| [1] | 陈尔学. 星载合成孔径雷达影像正射校正方法研究[D]. 北京:中国林业科学研究院, 2004. http://cdmd.cnki.com.cn/article/cdmd-82201-2005030713.htm |
| [2] | 张继贤, 魏钜杰, 赵争, 等. 基于多方向多源合成孔径雷达数据融合的假彩色正射影像制作[J]. 测绘学报 , 2011, 40 (3) : 276–282. |
| [3] | 侯家槐, 吕宝庆, 张俊. 基于RD模型的SAR影像正射纠正研究[J]. 测绘与空间地理信息 , 2012, 35 (4) : 100–103. |
| [4] | 张波, 侯四国, 张红, 等. R-D与共线模型在星载SAR影像正射纠正应用中的对比分析[J]. 武汉大学学报(信息科学版) , 2010, 35 (9) : 1069–1073. |
| [5] | ZHANG G, QIANG Q, LUO Y, et al. Application of RPC Model in Orthorectification of Spaceborne SAR Imagery[J]. Photogrammetric Record , 2012, 27 (137) : 94–110. DOI:10.1111/phor.2012.27.issue-137 |
| [6] | 张过, 李贞. 基于RPC的TerraSAR-X影像立体定向平差模型[J]. 测绘科学 , 2011, 36 (6) : 146–148. |
| [7] | 李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报 , 2012, 41 (3) : 317–322. |
| [8] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报 , 2012, 41 (2) : 191–198. |
| [9] | 张过, 汪韬阳, 李德仁, 等. 轨道约束的资源三号标准景影像区域网平差[J]. 测绘学报 , 2014, 43 (11) : 1158–1164. |
| [10] | ZHANG L, HE X Y, BALZ T, et al. Rational Function Modeling for Spaceborne SAR Datasets[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2011, 66 (1) : 133–145. DOI:10.1016/j.isprsjprs.2010.10.007 |
| [11] | 张过, 费文波, 李贞, 等. 用RPC替代星载SAR严密成像几何模型的试验与分析[J]. 测绘学报 , 2010, 39 (3) : 264–270. |
| [12] | 闫世勇. 角反射器雷达干涉实验及在形变监测中的应用[D]. 邯郸:河北工程大学, 2009. |
| [13] | XIA Y, KAUFMANN H, GUO X F. Landslide Monitoring in the Three Gorges Area Using D-InSAR and Corner Reflectors[J]. Photogrammetric Engineering & Remote Sensing , 2004, 70 (10) : 1167–1172. |
| [14] | 李莹莹, 吴昊, 俞雷, 等. 高分辨率SAR和可见光图像同名点自动匹配技术[J]. 测绘通报 , 2014 (5) : 66–70. |
| [15] | 张过, 墙强, 祝小勇, 等. 基于影像模拟的星载SAR影像正射纠正[J]. 测绘学报 , 2010, 39 (6) : 554–560. |