2. 中国测绘科学研究院, 北京 100830 ;
3. 四川省第一测绘工程院, 四川 成都 610100
北斗卫星导航系统具备了亚太区域的导航定位功能,提供三频观测信号,可以组合成多种波长较长、噪声较小的组合观测值,利于模糊度的实时快速固定,而相位模糊度的固定是实现厘米级RTK动态定位的关键。
GNSS三频观测值模糊度固定算法研究已有很多,其中RTK短基线三频模糊度单历元固定方法最为著名的是TCAR(three carrier ambiguity resolution)法和CIR(cascade integer resolution)方法。这两种算法原理上是相同的,利用不同伪距和相位组合其波长不同的特点,单颗卫星逐级(超宽巷—宽巷—窄巷)直接取整方式固定模糊度,算法非常简单,无须搜索,但容易出现模糊度固定错误。随着三频模糊度解算概念的扩展[1-2],基于几何模型的三频模糊度固定方法发展起来,将位置和模糊度同时作为待估参数求解,计算模糊度浮点解和方差阵,并使用最小二乘降相关搜索法(the least-squares ambiguity decorrelation adjustment methods,LAMBDA)固定模糊度,同样逐级固定超宽巷—宽巷—窄巷或基本频点模糊度。LAMBDA方法理论上讲是一种数学方法,计算量较大,可靠性较高,但仍存在区间次小和最小方差比值RATIO值大于设定阈值,即出现RATIO大但模糊度错误的情况,同样也会出现RATIO较小但模糊度正确的情况。Teunissen在2002年比较了TCAR、CIR和LAMBDA方法在三频模糊度解算中的应用,指出TCAR和CIR比较适合无几何模型的单星模糊度解算,LAMBDA适用于有几何模型的模糊度固定[3]。
TCAR方法单历元单星固定三频模糊度受观测噪声影响较大,容易出现模糊度误判固定错误,无法实现模糊度100%固定。为了实现北斗三频RTK单历元模糊度固定,本文基于三频组合观测值的组合特性选取了几组合适的超宽巷、宽巷组合观测值,发现超宽巷或宽巷组合双差残差与波长差异明显,如超宽巷波长4.8 m的组合双差残差一般在0.2 m左右,因此模糊度一旦固定错误,则引起整周波长倍数的粗差(至少4.8 m),超宽巷组合观测值单位权中误差会出现跳变异常(1周约1 m);类似的模糊度固定错误中误差异常跳变同样适用于宽巷和基本频点观测值。因此对三频TCAR方法进行了改进,在固定超宽巷、宽巷和基本频点模糊度时,附加观测值单位权中误差作为模糊度固定的标准。此算法对观测噪声较大模糊度直接取整容易出现错误的卫星给定2个备选模糊度,而观测噪声较小的卫星直接取整固定,从而形成少量备选模糊度向量组合,进而对备选模糊度组合分别判断观测值单位权中误差,其中最小中误差且中误差小于设定的阈值时对应的模糊度向量为固定解,逐级(超宽巷—宽巷—窄巷)固定模糊度。通过河北局域实测数据验证,此方法固定成功率为100%,克服了TCAR中模糊度直接取整误判问题。
一、 三频观测值及其线性组合 1. 伪距和相位观测值北斗具有3个频点(B1、B2和B3) 观测值,对于卫星S和接收机R相应的伪距和相位观测方程可以表示为[4]
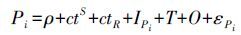 (1)
(1) 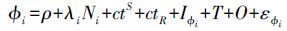 (2)
(2) 式中,P为伪距观测值;φ为载波相位观测值;ρ为站星间几何距离;c为光速,即299 792 458 m/s;tS为卫星钟差;tR为接收机钟差;IPi为相应频率伪距电离层延迟;T为对流层延迟;O为星历误差;i为频点(B1、B2、B3);εPi为伪距观测噪声;λi为波长;Ni为整周模糊度;Iφi为相应频率相位电离层延迟;εφi为相位观测噪声。
2. 最优三频组合观测值选取为了单历元实现模糊度固定,组合观测值应该具有更长的波长、更小的噪声和电离层影响,三频观测值可以组合成很多相应的观测值。根据相关文献关于三频组合观测值的特性的研究[5-8],三频观测值线性组合可以表示为
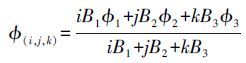 (3)
(3) 组合频率为
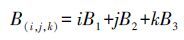 (4)
(4) 组合波长为
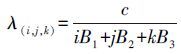 (5)
(5) 组合整周模糊度为
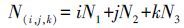 (6)
(6) 组合电离层延迟一阶放缩因子
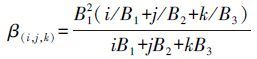 (7)
(7) 假设3个频率观测值等精度,组合观测噪声为
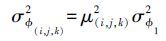 (8)
(8) 噪声因子为
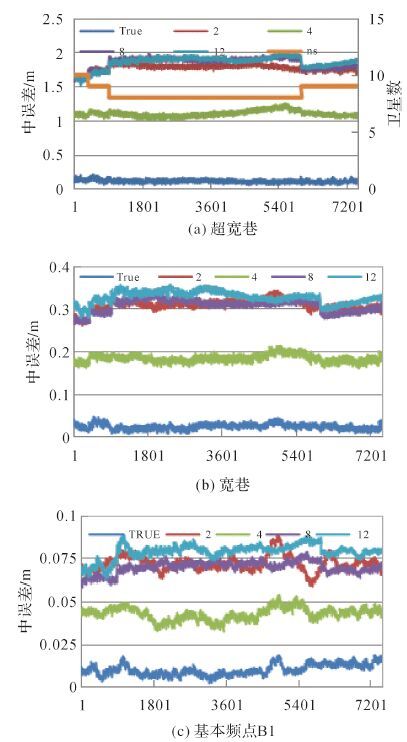
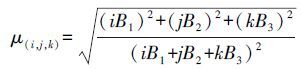 (9)
(9) 常用的组合观测值见表 1,φ0, 1, -1由于具有4.8 m的长波长,称为超宽巷组合(EWL),φ1, -1, 0、φ1, 0, -1波长分别约为0.86和1.02 m,称为宽巷组合(WL)。本文中采用的宽巷组合波长为0.86 m,B1、B2和B3称为基本频点模糊度。
| 组合系数 | λ(i, j, k)/m | β(i, j, k) | μ(i, j, k) | ||
| 1 | 0 | 0 | 0.19 | 1.00 | 1.00 |
| 0 | 1 | 0 | 0.24 | 1.67 | 1.00 |
| 0 | 0 | 1 | 0.23 | 1.51 | 1.00 |
| 0 | 1 | -1 | 4.88 | -1.59 | 28.53 |
| 1 | -1 | 0 | 0.84 | -1.29 | 5.57 |
| 1 | 0 | -1 | 1.02 | -1.23 | 6.87 |
观测值模糊度固定后,观测残差主要是差分后大气延迟残差和观测噪声,一般模糊度固定错误造成观测值出现波长整周倍数的粗差,粗差和正常残差大小相差悬殊,如超宽巷模糊度粗差一般为4.8 m,正常差分后的残差为0.2 m左右,最小二乘估计是均方误差最小的参数估计,粗差与正常残差的大小悬殊必然引起定位偏差,并直接反映在中误差上。粗差引起中误差的变化大小与样本空间的大小,即卫星个数、模型结构即(卫星图形),以及出现粗差的样本(哪颗卫星)有关。
图 1为2、4号GEO,8号IGSO和12号MEO模拟超宽巷、宽巷和基本频点模糊度固定错1周引起的中误差值变化。从图中可以看出,粗差与残差的大小悬殊导致错误中误差与真值差异明显,且较高卫星与卫星数有关,而较低4号GEO卫星对中误差影响比较平缓,但与真值差异同样明显。总之,模糊度固定错误(发生跳周引入粗差时中误差明显大于真值),可以作为模糊度固定参考指标。
|
| 图 1 模糊度错1周引起的中误差变化 |
将式(1) 和式(2) 组成双差观测方程,再相减用于模糊度浮点解计算。常规TCAR方法认为残差(电离层、观测噪声等)对载波影响小于半周,顾及整数特性直接取整获得固定解。当观测噪声和电离层残差较大时容易出现模糊度固定错误,此时本文用TCAR计算的模糊度建立少量备选模糊度组合,前文分析可知模糊度固定错误会引起中误差跳变,因此引入中误差作为模糊度固定的附加判断标准,相应的模糊度固定步骤如下:
1) 忽略残差影响,应用式(10) 计算组合观测值模糊度浮点解ΔΔN,四舍五入取整得ΔΔ N。
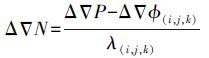 (10)
(10) 2) 当|ΔΔN-[ΔΔN]|≤δ时,[ΔΔN]为模糊度固定解。
3) 当|ΔΔN-[ΔΔN]>δ|时,取ΔΔN两边的整数为备选模糊度。即ΔΔN-[ΔΔN]>δ时,取[ΔΔN]和[ΔΔN+0.5];ΔΔN-[ΔΔN] <δ时,取[ΔΔN]和[ΔΔN-0.5]。
4) 当前历元所有卫星通过步骤1) —步骤3) 后,建立了备选模糊度向量组合,进而对备选模糊度向量计算中误差,其中最小且小于设定阈值的中误差对应的模糊度向量为固定解。
按照步骤1) —步骤4) 依次固定超宽巷、宽巷和基本频点B1模糊度。当固定超宽巷时,P为伪距;固定宽巷时,P为超宽巷;固定B1时,P为宽巷。
四、 试验分析采用河北区域实际测量数据进行实例分析,采用和芯星通370三频接收机,观测时间2015年6月4号中午12:00—14:00,数据采样率为1 s,基线长度为10.8 km,卫星截止高度角为15°。测站准确坐标用GPS数据静态解算获得。
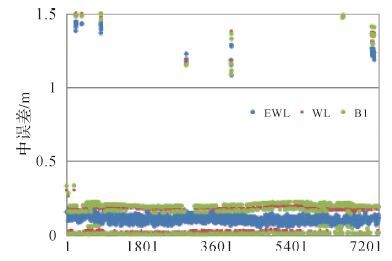
表 2统计了常规TCAR方法全部历元中出现模糊度固定错误的卫星情况,宽巷是采用正确超宽巷模糊度下固定错误统计、B1是正确宽巷下错误统计,显然三者同时固定错误的历元很少,互不相关。图 2显示了4号GEO卫星超宽巷、宽巷和基本频点B1的模糊度浮点解,线条的粗心反映了组合观测值的组合噪声大小,当偏差大于0.5周时,直接取整固定错误,其中宽巷模糊度37%固定错误。
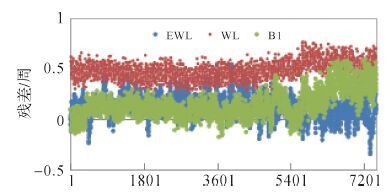
|
| 图 2 4号GEO卫星超宽巷、宽巷、B1浮点解 |
图 3显示了TCAR方法固定超宽巷、宽巷和基本频点B1模糊度后相应的观测值中误差值。超宽巷模糊度固定错误会引起宽巷和B1模糊度固定错误,并且超宽巷、宽巷和B1的中误差大小差不多,明显大于超宽巷观测值中误差数量级;宽巷模糊度固定错误同样引起B1模糊度固定错误,并且宽巷与B1的中误差大小差不多,明显大于宽巷观测值中误差数量级;而B1模糊度固定错误时,B1的中误差明显大于B1观测值中误差数量级。因此模糊度固定正确时,观测值中误差明显小于固定错误时,并且差异明显。
|
| 图 3 TCAR方法中误差 |
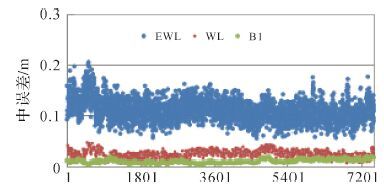
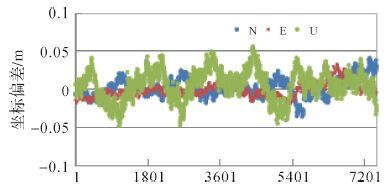
图 4 显示了采用文中所述方法固定模糊度后相应的超宽巷、宽巷和B1频点观测值中误差值,其中没有较大的跳点值,并且图 5分别显示了B1使用固定的模糊度的定位偏差值,平面定位偏差优于3 cm,高程优于5 cm。因此附加中误差约束的TCAR搜索法实现了模糊度100%固定,克服了TCAR直接取整模糊度误判问题。
|
| 图 4 TCAR搜索法的中误差 |
|
| 图 5 基本频点B1定位偏差 |
本文提出的附加中误差约束的TCAR搜索法引入观测值中误差作为模糊度固定的判断标准,对TCAR方法建立的少量备选模糊度向量组进行搜索,其中中误差最小值对应的模糊度向量为固定解,实现了北斗三频RTK单历元模糊度实时固定。经实测数据验证,超宽巷、宽巷和B1模糊度的固定成功率达到100%,克服了常规TCAR方法直接取整的模糊度误判的弊病,从而实现了三频单历元RTK厘米级定位。
| [1] | 范建军, 王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报 , 2007, 36 (1) : 43–49. |
| [2] | 刘炎炎, 叶世榕, 江鹏, 等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报(信息科学版) , 2015, 40 (2) : 209–213. |
| [3] | TEUNISSEN P J G, JOOSTEN P. A Comparison of TCAR, CIR and LAMBDA GNSS Ambiguity Resolution[C]//Proceedings of ION GPS. Portland, Oregon:[s.n.], 2002:2799-2808. |
| [4] | 程鹏飞, 蔡艳辉, 文汉江, 等. 全球卫星导航系统GPS, GLONASS, Galileo及其他系统[M]. 北京: 测绘出版社 ,2009 . |
| [5] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy , 2008 (82) : 847–862. |
| [6] | COCARD M, BOURGON S, KAMALI O, et al. A Systematic Investigation of Optimal Carrier-phase Combinations for Modernized Triple-frequency GPS[J]. Journal of Geodesy , 2008 (82) : 555–564. |
| [7] | 张小红, 何锡扬. 北斗三频相位观测值线性组合模型及特性研究[J]. 中国科学(地球科学) , 2015, 45 (5) : 601–610. |
| [8] | 黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报 , 2012, 41 (5) : 763–768. |


