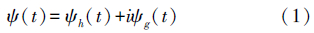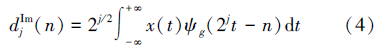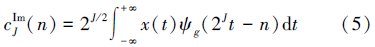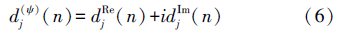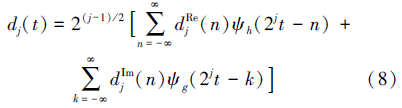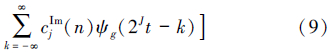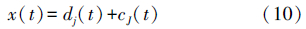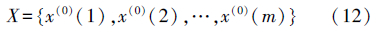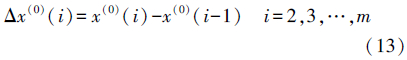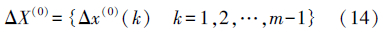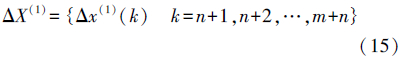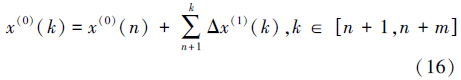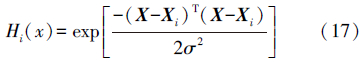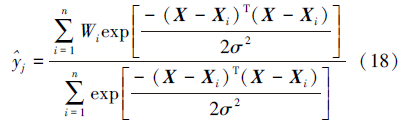2. 广西空间信息与测绘重点实验室,广西 桂林 541004;
3. 广西城市建设学校,广西 桂林 541004
卫星钟差(satellite clock bias,SCB)的预报是一项非常重要的工作,钟差预报的可靠程度直接决定导航精度,研究钟差预报有利于提高参数预报的可靠性和准确性,优化卫星钟差改正数据上传时间间隔;而且在实时动态精密单点定位中需要采用钟差预报结果参与计算来实现高精度定位[1, 2]。因此,提高导航卫星钟差预报的精度尤为重要。然而,空间中的卫星钟容易受到各种因素的影响[3],如温度、电离层、磁场等环境因素,导致了卫星钟差存在较为复杂的变化。而且,载原子钟频率总的波动是白噪声调相、白噪声调频、闪变噪声调相、闪变噪声调频以及随机游走调频5种噪声线性叠加的结果[4],这些使得建立精准的星载原子钟运行模型变得较为困难,也不利于建立高精度的钟差预报模型。因此,针对钟差预报,国内外许多学者已经研究出了多种方法,主要有:线性模型、二次多项式模型、灰色模型、卡尔滤波模型等[5, 6, 7],但这些模型均仅适用于卫星钟差处于平稳的情况下,而星载原子钟频率高且非常敏感,极易受到外界及其自身因素的影响,很难掌握其复杂细致的变化规律,往往卫星钟差呈非平稳变化[3]。文献[8]指出,一个变化异常复杂的非线性、非平稳随机序列很难使用单一的模型进行有效预报。近年来,随着机器学习理论的不断发展,神经网络由于其在非线性系统建模与优先求解方面的优势,已在预测控制中得到较为广泛的应用,也出现了多种多样的神经网络控制算法[9],其中,广义回归神经网络由于具有良好的逼近非线性模型的性能和有能力得到较为稳定的结果而得到了广泛应用。
因此,本文结合钟差数据的特点,利用小波原理在信号特征分析中的优势和广义回归神经网络(generalized regression neural network,GRNN)在非线性时间序列预报方面的优良特性,建立了将双树复小波和广义回归神经网络相结合的卫星钟差预报方法。首先利用双树复小波[10]将钟差时间序列分解成具有不同频率特征的分量;然后根据各分量的特点分别构建高频和低频广义回归神经网络模型进行预报,其中,考虑到低频分量的数据位数过多,预先进行一次差处理再建立低频预报模型;最后将各分量的预报结果进行叠加得到最终的钟差预报值。以IGS提供的5 min采样率的精密钟差序列作为算例,与灰色模型、最小二支持向量机和广义回归神经网络进行对比分析,探讨和研究本文方法对不同原子钟类型以及不同预报长度的可行性和有效性。
一、算法原理 1. 双树复小波变换Kingsbury 等于1998年首次提出了双树复小波(dual-tree complex wavelet transform,DTCWT) 的概念[10],成功克服了离散小波变换不具有平移不变性和会造成频率混叠的缺陷。2005 年,双树复小波变换分解与重构的算法又被 Selesnick 等进一步构出[11]。双树复小波变换[10, 11]作为一种新型的小波变换方法,具有近似平移不变性、良好的方向选择性、有限的数据冗余性、完全重构性和计算效率高等优良特性。目前,已在图像处理、语音处理、振动信息提取等[12, 13, 14]领域被广泛应用。其原理如下:
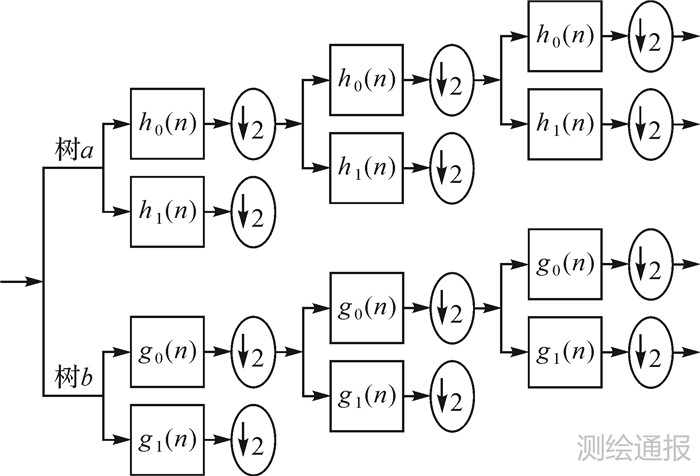
双树复小波变换是采用二叉树结构( 树a和树b) 的两路离散小波变换,树a生成实部,而树b生成虚部。对于一维信号,分解流程如图 1 所示,其中,h0(n)、h1(n)表示共轭正交滤波器对;g0(n)、g1(n)表示共轭积分滤波器对;↓2表示各点采样。
|
| 图 1 一维双树复小波变换原理 |
根据DTCWT的构造方法,复小波可表示为
式中,ψh(t)、ψg(t)表示两个实小波;i为复数单位。由于DTCWT由两个平行的小波变换组成,因此,根据小波理论,图 1中,虚线上面实部树小波变换的小波系数和尺度系数可分别表示为
同理,虚部树小波变换的小波系数和尺度系数可分别表示为
由此可得DTCWT的小波系数和尺度系数为
通过式(8)和式(9)对DTCWT的小波系数和尺度系数进行重构
因此,双树复小波变换后的重构信号可表示为
最后,原始信号x(t)的重构信号可表示为
式中,TRe为小波分解的实部树系数;TΙm为小波分解的虚部树系数。 2. 钟差一次差预报原理根据原子钟的钟差数值可知,相邻历元的数值相差不大,对钟差序列相邻历元间作一次差,可得到有效数字位数减少的数据序列。设一组不同历元时刻的钟差值为
对该序列相邻历元作一次差得
得到一组新的时间序列
设ΔX(0)钟差序列对应的时间为tk(k=1,2,…,m-1),建立广义回归神经网络预报n个历元以后的一次差序列
最后,通过一次差预报序列和钟差值x(0)(m)对应相加即得到所求历元的钟差
3. 广义回归神经网络GRNN是美国学者Donald F. Specht在1991年提出的,它是一种改进的径向基神经网络,在逼近能力和学习速度上较RBF网络有更强的优势,其模型的泛化性能良好。
GRNN网络结构由输入层、模式层、求和层和输出层组成,输入层不处理信息,只为模式层分配输入信息,输入层神经元数目等于学习样本中输入向量的维数[15]。模式层与输入层全部相连,其神经元数目同学习样本的数目相同,神经元传递函数为
式中,X为输入向量;i未输入样本的数目,i=1,2,…,n;σ为平滑参数,是GRNN仅有的一个人为调节参数,学习能力很强,对网络输出影响比较大,并且基本依赖样本数据。求和层神经网络应用权重Wi和模式层神经元的输出信号Hi(X),根据公式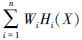 进行计算。
进行计算。
输出层神经元数目等于学习样本的输出向量的维数j,其实际执行除运算,即
二、算 例 1. 试验数据以2013年7月7日至2013年7月10日IGS提供的5 min采样率的精密钟差数据为例,为使试验更具代表性和一般性,本文选择不同类型钟所对应的卫星进行试验: BLOCK II A铯钟-PRN08和10、BLOCK II A铷钟-PRN04、BLOCK II R铷钟-PRN18和28、BLOCK IM铷-PRN31。
2. 钟差预报过程1) 采用双树复小波对原始钟差序列进行分解,得到一系列不同频率特征的分量。
2) 分别建立低频和高频GRNN预报模型,确定网络的输入、输出量。对于低频模型,输入量为实际分解的分量值;对于高频模型,输入量为经一次差后的值;两种模型的输出量分别为对应的实际值。
3) 根据已知数据,进行学习集和样本集的分配。
4) 网络建立:采用Matlab神经网络工具箱函数建立GRNN,并通过交叉验证方法来确定网络最佳的平滑参数。
5) 网络训练:利用学习集对GRNN进行训练。
6) 网络仿真:利用训练好的GRNN进行钟差预报。
3. 试验分析为验证本文算法的可行性、有效性和优越性,建立4种预报方案进行对比分析:灰色GM(1,1)预报模型,最小二乘支持向量机预报模型,单一的GRNN预报模型,以及基于DTCWT的GRNN预报模型。考虑到IGS的钟差数据以5 min为间隔单位,本文选取前144历元作为模型的训练样本,预报长度为未来12 h、24 h、36 h、48 h、60 h和72 h,分别对所选的卫星钟进行预报,并以IGS相应的精密钟差值为基准,使用均方根误差(RMS)作为统计量。其中,方案 1—方案 3直接采用原始数据进行建模,方案 4采用经小波分解重构后的分量建模,为了加快GRNN的收敛速度和降低建模误差,方案 1—方案 3在建模预报时,所有的钟差序列归一化到[-1-1]区间,经模型预报后再还原到原始区间。对于方案 4的低频分量,考虑到数据位数给模型带来的误差,先进行一次差处理,然后利用前143个差值建立GRNN预报模型。
对于小波分解,需要确定分解级数,往往根据信号特征来选择,分解层数越多,分解和重构过程中产生的计算误差越大,计算上的误差会带到预报的误差中,使预报精度下降;相反,如果分解层数过少,则无法体现信号在不同频带上的变化特征[16]。通过试验比较分析发现,一般情况下,进行3~5层分解便可达到理想效果。因此,本文采用双树复小波对钟差序列进行三层分解,原钟差时间序列及其分解后的各个分量如图 2所示。
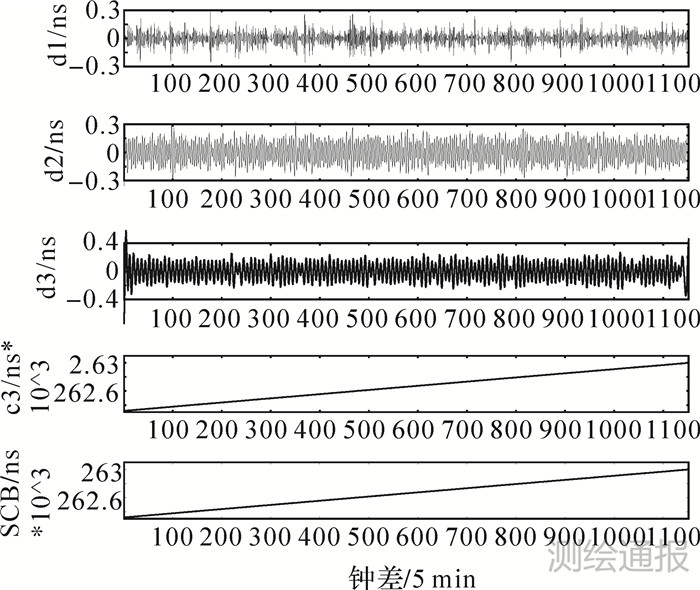
|
| 图 2 PRN18钟差序列的分解结果 |
由图 2可看出,d1至c3序列明显趋于平稳,频率依次降低。针对低频分量c3,先进行一次差值处理,结果如图 3所示。

|
| 图 3 PRN18钟差序列的一次差值 |
由图 3对比原始钟差序列,显然,经一次差后的钟差值变化更有利于GRNN模型的建立预报。各分量的预报误差如图 4所示(预报长度为12 h),可见,各分量的预报值与实际值的差值相差很小。对各分量的预报结果进行叠加,得到最终的预报结果,预报误差如图 5所示。
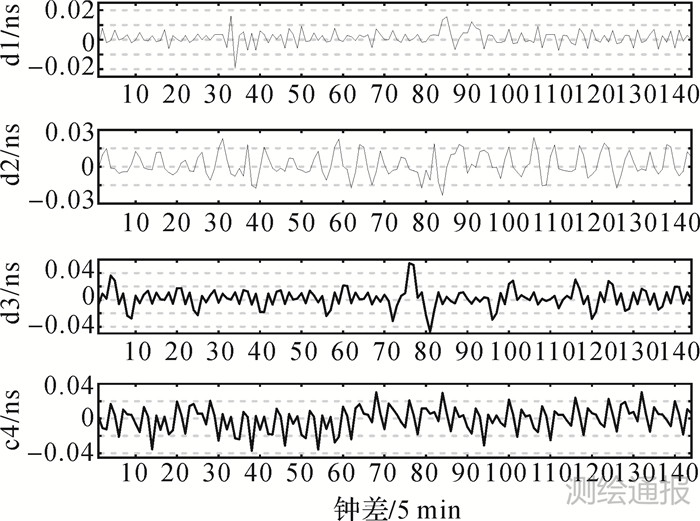
|
| 图 4 各个分量的预报误差 |
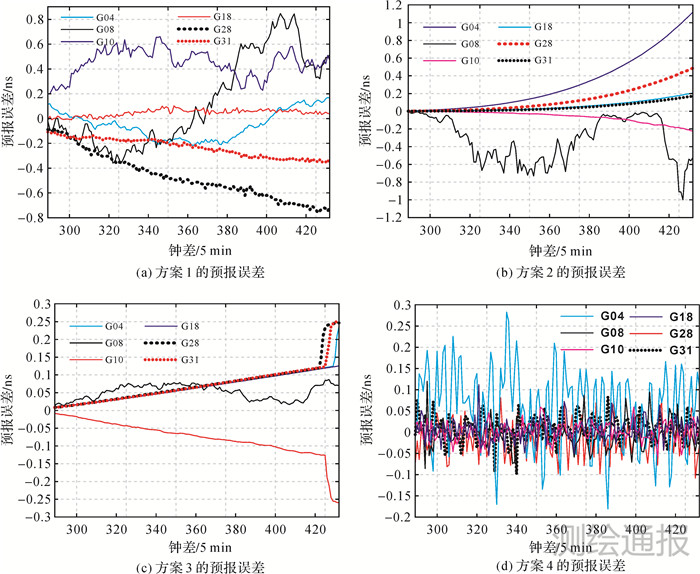
|
| 图 5 各卫星钟差的预报误差 |
与PRN18卫星钟差的预报过程相似,采用双树复小波对原始钟差序列进行自适应分解,采用GRNN对其余5颗卫星的钟差进行预报。限于篇幅,仅给出了预报长度为12 h的误差对比图,如图 5所示。为进一步分析不同预报长度下的效果,表 1给出了各卫星钟差不同预报长度的预报结果统计值,以RMS作为统计标准。
| ns | |||||||
| 预报模型 | 卫星钟 | 不同预报长度/h | |||||
| 12 | 24 | 36 | 48 | 60 | 72 | ||
| 灰色GM(1,1) | G04 | 0.141 | 0.197 | 0.343 | 0.592 | 0.895 | 1.220 |
| G08 | 0.392 | 0.474 | 0.708 | 0.877 | 0.877 | 0.843 | |
| G10 | 0.327 | 0.338 | 0.342 | 0.345 | 0.389 | 0.466 | |
| G18 | 0.085 | 0.095 | 0.114 | 0.138 | 0.161 | 0.212 | |
| G28 | 0.511 | 0.764 | 1.059 | 1.371 | 1.760 | 2.220 | |
| G31 | 0.253 | 0.370 | 0.438 | 0.481 | 0.524 | 0.563 | |
| 最小支持向量机 | G04 | 0.449 | 0.592 | 0.691 | 0.732 | 0.922 | 1.252 |
| G08 | 0.412 | 0.481 | 0.506 | 0.618 | 0.636 | 1.138 | |
| G10 | 0.109 | 0.165 | 0.733 | 0.893 | 0.962 | 1.012 | |
| G18 | 0.105 | 0.212 | 0.495 | 0.710 | 0.770 | 1.144 | |
| G28 | 0.106 | 0.202 | 0.604 | 0.713 | 1.374 | 1.578 | |
| G31 | 0.589 | 0.684 | 0.724 | 1.393 | 1.676 | 2.308 | |
| 广义回归神经网络 | G04 | 0.103 | 0.232 | 0.315 | 0.393 | 0.468 | 0.541 |
| G08 | 0.087 | 0.169 | 0.258 | 0.322 | 0.406 | 0.495 | |
| G10 | 0.113 | 0.229 | 0.315 | 0.390 | 0.466 | 0.539 | |
| G18 | 0.099 | 0.230 | 0.315 | 0.393 | 0.468 | 0.541 | |
| G28 | 0.114 | 0.230 | 0.314 | 0.390 | 0.467 | 0.541 | |
| G31 | 0.109 | 0.234 | 0.320 | 0.396 | 0.470 | 0.541 | |
| 本文算法 | G04 | 0.117 | 0.168 | 0.210 | 0.258 | 0.289 | 0.327 |
| G08 | 0.048 | 0.083 | 0.101 | 0.132 | 0.180 | 0.273 | |
| G10 | 0.028 | 0.034 | 0.046 | 0.050 | 0.065 | 0.096 | |
| G18 | 0.028 | 0.030 | 0.033 | 0.043 | 0.051 | 0.071 | |
| G28 | 0.043 | 0.046 | 0.049 | 0.055 | 0.061 | 0.076 | |
| G31 | 0.030 | 0.035 | 0.042 | 0.051 | 0.068 | 0.102 | |
由图 5可看出,方案 1—方案 3的预报不稳定,预报残差呈上升趋势,不利于较长时间的预报;方案 1对于PRN18的预报效果较好,方案 3对PRN08的预报效果较为稳定,而本文方法的预报误差较小,变化较为平缓。由表 1可进一步分析,随着预报长度的增加,各种预报方法的预报精度都出现不同程度的变化,方案 1、方案 2的预报精度明显降低,方案 3的预报精度优于方案 1和方案 2,而方案 4的预报精度远优于其他预报方法,误差增加幅度较小。综上,本文算法不仅能保证较优的局部预报值,而且具有较好的全局预报精度。因此,当卫星钟差变化较为复杂,需要进行更长时间的预报时,采用本文方法能够取得较好的预报效果。
三、结 论针对呈非线性、非平稳性的卫星钟差,本文提出了将双树复小波和GRNN相结合进行钟差预报,理论分析和算例表明:
1) 利用双树复小波对钟差时间序列进行分解,可得到一系列不同频率的分量;并对其采用GRNN建模预报,试验结果表明,该方法可行、有效。
2) 统计分析结果表明,本文方法对于不同长度的预报精度明显优于单一的灰色GM(1,1)、LSSVM和GRNN模型,表明该方法具有较高的预报能力和较好的预报精度,应用于卫星钟差的预报更具优越性,为钟差预报提供了新的思路。
3) 卫星钟差存在较为复杂的变化,建立一个更为准确的原子钟预报模型还比较困难,有待进一步的研究。
| [1] | GOTOH T. Improvement GPS Time Link in Asia with All in View[C]//Proceedings of the 2005 IEEE International Frequency Control Symposium (FCS) and Exposition. Vancouver. BC: IEEE, 2005. |
| [2] | HOU J, DONG S W, QU L L, et al. Real-time Solution of Atomic Clock Operating Parameters Based on Adap-tive Kalman Filtering[J]. Chinese Astronomy and Astrophysics, 2013, 37(1):90-96. |
| [3] | HEO Y J, JEONGHO C, HEO M B. Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behaviour[J]. Measurement Science and Technology, 2010, 21(7):110-118. |
| [4] | ALLAN D W. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987, 34(6):647-654. |
| [5] | VERNOTTE F, DELPORTE J, BRUNET M, et al. Uncertainties of Drift Coefficients and Extrapolation Errors:Application to Clock Error Prediction[J]. Metrologia, 2001, 38(4):325. |
| [6] | 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2005, 30(5):447-450. |
| [7] | 朱祥维, 肖华, 雍少为, 等. 卫星钟差预报的Kalman算法及其性能分析[J]. 宇航学报,2008, 29(3):966-970. |
| [8] | HUANG N E, WU M L, QU W D, et al. Applications of Hilbert-Huang Transform to Non-stationary Financial Time Series Analysis[J]. Applied Stochastic Models in Business and Industry, 2003, 19:245-268. |
| [9] | 戴文战, 娄海川, 杨爱萍. 非线性系统神经网络预测控制研究进展[J]. 控制理论与应用, 2009, 26(5):521-530. |
| [10] | KINGSBURY N G. The Dual-tree Complex Wavelet Transform: a New Technique for Shift Invariance and Directional Filters[C]//Proceedings of the 8th IEEE Digital Signal Processing Workshop. Bryce Canyon:IEEE, 1998:2-5. |
| [11] | SELESNICK I W, BARANIUK R G, KINGSBURY N G. The Dual-tree Complex Wavelet Transform[J]. IEEE Signal Processing Magazine, 2005, 22(6):123-151. |
| [12] | 翟振兴. 基于小波变换的信号去噪研究[D]. 重庆:重庆大学, 2010. |
| [13] | 王娜, 郑德忠, 刘永红. 双树复小波包变换语音增强新算法[J]. 传感技术学报, 2009, 22(7):983-987. |
| [14] | 吴定海, 张培林, 任国全, 等. 基于双树复小波包的发动机振动信号特征提取研究[J]. 振动与冲击, 2010, 29(4):160-163,176. |
| [15] | 陈娇, 王永泓, 翁史烈. 广义回归神经网络在燃气轮机排气温度传感器故障检测中的应用[J]. 中国电机工程学报, 2009, 29(32):92-97. |
| [16] | 徐科, 徐金梧, 班晓娟. 基于小波分解的某些非平稳时间序列预测方法[J]. 电子学报, 2001, 29(4):566-568. |