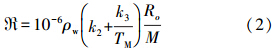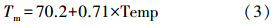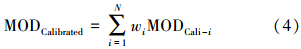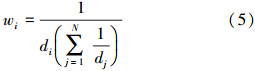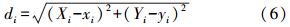一、引 言
Goldstein于1995年首次研究了大气对InSAR的影响,发现了由低空大气层动态水汽含量引起的大气延迟误差,延迟误差均方根误差为0.24 cm[1]。Tarayre等利用ERS-1雷达数据发现可以反演对流层的水汽现象,分辨率可达40 m[2]。Sandwell等提出了基于多幅差分干涉图的相位梯度算法以削弱对流层和电离层造成的大气延迟误差的理论[3]。Williams等利用美国California的GPS网络获取的数据解算出了每个站点的总大气延迟量,有效地削弱了沉降监测结果中的大气延迟误差;同时发现了在长基线干涉测量中水汽湿延迟遵循Treuhaft-Lanyi统计模型[4]。Webley等利用欧洲埃特纳火山的ERS-2卫星数据提取了不同时期的地表沉降量,同时基于GPS观测数据反演了大气水汽含量IWV。结果表明同时期内IWV最大为10 kg/m3[5]。Li等在试验中利用MERIS大气产品改正了ASARD-InSAR监测结果中的水汽信息[6]。斯坦福大学的Fayaz Onn研究了通过稀疏的地面GPS观测数据模拟大气中的水汽含量和延迟影响,从而对InSAR进行误差改正[7]。本文通过利用广东地区的GPS网络数据和MODIS数据对TerraSAR-X数据干涉图中的大气改正作了一些尝试性的研究。
二、GPS对流层湿延迟与水汽含量反演 1. 反演模型广东地区的6个CORS站点的数据和对应时间上的MODIS数据被用来作比较研究,站点的分布如图 1所示,使用的数据时间段和本文中所用到的SAR影像的获取时间相一致。同时从IGS官网下载了国内昆明、上海、西安3个站点的o文件、精密星历与导航电文。MODIS的水汽产品给出的是可降水汽(precipitable water vapour,PWV),因此经过Gamit软件处理后得到的GPS-ZWD需要通过式(1)转换为GPS-PWV。而GPS-PWV数据需要通过云掩膜产品去除有云存在的像素(置为零)。站点采用WGS-84坐标系,处理过程采用多基线解算方法,将昆明点作为起始解算点。最终解算得到了6个站点的空间坐标、天顶湿延迟和水汽含量
式中,R为无量纲的转换因子,即式中,ρw表示水密度;TM表示大气平均温度;M表示液态水摩尔质量;k2与k3表示大气折射常数。通常R变化不大,取值范围为6~7。本文中根据GPS解算的天顶湿延迟和PWV得出各站点的转换因子,然后取平均值。
(1) GPS天顶湿延迟解算方案
Gamit处理GPS数据方案见表 1。
| 解算方法 | RELAX | 观测值类型 | LC_AUTCLN |
| 分析值类型 | 1-ITER | 时间间隔/s | 30 |
| 卫星截止高度角 | 15° | 天顶延迟模型 | PWL |
| 干延迟映射函数 | GMF | 湿延迟映射函数 | GMF |
(2) 水汽解算结果
基线解算的精度见表 2。
精度符合一般要求(小于0.5),表明数据可用。最终获取的各GPS站点天顶向总延迟、湿延迟及水汽含量见表 3。
| 时间 | 站点名称 | (GPS-ZWD)/cm | (GPS-PWV)/cm | 转换因子 |
| 2009-12-28 | DMGT | 16.371 | 2.659 | 6.156 825 874 |
| 2009-12-28 | JMGT | 16.409 | 2.663 | 6.161 847 54 |
| 2009-12-28 | NLGT | 16.156 | 2.623 | 6.159 359 512 |
| 2009-12-28 | ZHGT | 17.165 | 2.786 | 6.161 162 958 |
| 2009-12-28 | ZSGT | 16.188 | 2.627 | 6.162 162 162 |
| 2010-03-04 | JMGT | 24.995 | 4.057 | 6.160 956 372 |
| 2010-03-04 | NLGT | 26.806 | 4.352 | 6.159 466 912 |
| 2010-03-04 | ZHGT | 27.213 | 4.417 | 6.160 968 983 |
| 2010-03-04 | ZSGT | 25.618 | 4.157 | 6.162 617 272 |
| 2010-05-09 | DMGT | 35.77 | 5.809 | 6.157 686 349 |
| 2010-05-09 | JMGT | 35.667 | 5.79 | 6.160 103 627 |
| 2010-05-09 | JWGT | 35.23 | 5.719 | 6.160 167 862 |
| 2010-05-09 | NLGT | 35.524 | 5.768 | 6.158 807 212 |
| 2010-05-09 | ZHGT | 36.264 | 5.886 | 6.161 060 143 |
| 2010-05-09 | ZSGT | 35.411 | 5.746 | 6.162 721 893 |
本文研究采用Terra平台的MOD05_L2级可降水汽产品,可从NASA官网上免费下载,空间分辨率为1000 m×1000 m。为了对InSAR结果进行有效改正,结合同期云掩膜去除了可能存在污染的像素。
3. GPS与MODIS可降水量的整体拟合改正基于上述分析可知,GPS大气可降水量与MODIS大气可降水量存在较高的相关性,其相关系数高于0.9。而整体上MODIS-PWV与GPS-PWV存在偏差且GPS解算大气水汽的精度较高。因此,可利用GPS站点天顶向PWV与MODIS-PWV的相关性进行最小二乘线性拟合,基于线性方程改正MODIS-PWV,以提高MODIS大气水汽含量的精度,为D-InSAR大气改正提供较高精度的对流层大气水汽分布图,进而得到对流层湿延迟改正图。这是本文中融合GPS与MODIS数据改正D-InSAR大气误差的方法。
(1) GPS和MODIS水汽数据对比
由于GPS观测站气象数据缺失,因此在解算天顶湿延迟与对流层水汽含量的转换因子时,其地表温度计算方式为
式中,Tm表示地表平均温度;Temp表示某点的地表温度。
由GPS-ZWD与GPS-PWV求得其转换因子,在试验中取平均值6.16,同时是MODIS反演天顶湿延迟的转换因子。上述MODIS可降水汽图覆盖了整个试验区域。
将上述MODIS水汽值与GPS解算的水汽值进行比较,其散点分布如图 1所示。
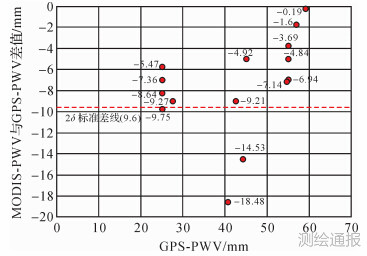 |
| 图 1 MODIS-PWV与GPS-PWV水汽差分散点分布 |
可以看出,MODIS水汽值平均值为4.3 cm,GPS平均值为3.5 cm。二者差值平均为-0.75 cm,标准差为0.466。其中有两个点超过两倍标准差,应视为粗差予以去除。利用Matlab根据其余GPS点水汽值与MODIS进行最小二乘线性拟合,求得MODIS水汽改正方程。
(2) 可降水量整体改正
利用上述线性改正方程对MODIS水汽值进行改正,经GPS改正后的MODIS水汽值效果较好,其平均值为4.2 cm,与GPS水汽值的差值均值由-0.75 cm降至-0.12 cm,改正后差值标准差为0.824,与之前相比降低了82.4%。可见将GPS较高精度的大气水汽值与MODIS结合起来,利用最小二乘线性拟合可以有效地提高MODIS水汽精度。这对于精确反演D-InSAR大气延迟改正图有重要的意义。
4. 顾及空间关系的GPS与MODIS可降水汽局部改正由于GPS空间密度较低,且分布十分离散。因此利用整体改正存在空间上的误差。宋小刚等认为利用同期GPS-PWV拟合方程对整幅MODIS-PWV进行改正无法体现大气水汽场空间分布及变化特性,因此可利用GPS站点的时空水汽含量与MODIS水汽含量进行单点分块改正[8]。
本文考虑了GPS站点空间分布与水汽变化的关系,提出并实现了考虑GPS-MODIS空间距离影响的局部改正算法,其基于欧氏距离构建权重因子对MODIS-PWV进行有效改正,数学模型如下
式中,MODCalibrated表示改正后的MODIS水汽值;MODCali-i表示根据第i个GPS点的线性拟合方程改正后的MODIS水汽值;N表示GPS站点数量;wi表示与空间距离相关的影响权重,距离越远对水汽变化的影响越小,权重也越小权;di表示GPS点与待改正MODIS像元的空间距离。各GPS点拟合方程见表 4。| GPS站点 | 最小二乘线性方程 | 相关系数 |
| JMGT | y=1.148 1x-16.828 | 0.87 |
| NLGT | y=1.035 5x-9.404 1 | 0.88 |
| ZHGT | y=1.292 4x-17.552 | 0.98 |
| ZSGT | y=1.014 3x-8.433 8 | 0.972 |
根据上述局部改正模型及拟合方程对所有的MODIS-PWV进行局部改正。
三、考虑大气延迟改正的二轨法D-InSAR形变监测试验及分析根据Terrasar-x成像参数和每个像素的绝对相位差,经过地理编码可以获取区域地表沉降监测初步结果。图 2、图 3为利用D-InSAR技术初步提取的地表沉降格局。可以看出在2010年这一时段内有部分沉降漏斗。同时图中圆圈区域偏差较大,主要是受山体地形和植被覆盖的影响,对流层底部水汽含量变化很大,引入了较大的大气延迟误差。因此需要进一步进行大气改正。
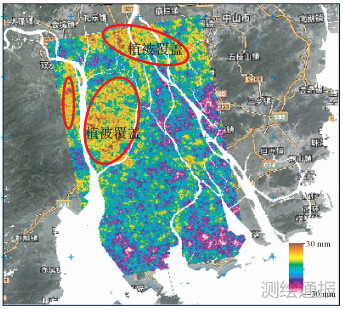 |
| 图 2 2009年12月—2010年3月D-InSAR初步监测 |
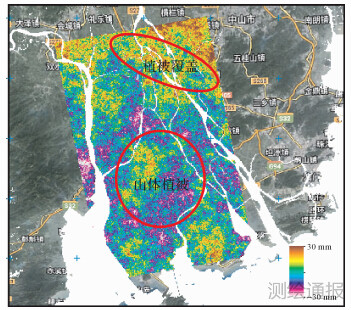 |
| 图 3 2010年3月—2010年5月D-InSAR初步监测 |
图 4、图 5为利用MODIS反演的大气延迟图改正结果。
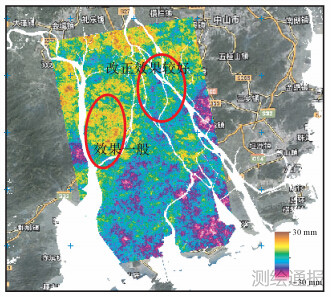 |
| 图 4 2009-12-28—2010-03-04干涉对MODIS改正 |
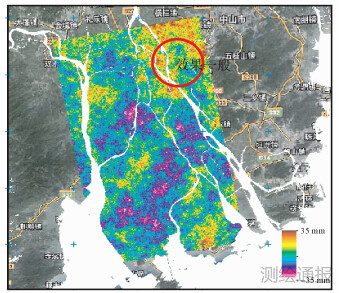 |
| 图 5 2010-03-04—2010-05-09干涉对MODIS改正 |
从图 5中可以看出,利用MODIS05_L2水汽值改正大气延迟误差结果整体精度较低,局部效果较好。
将图 6大气延迟改正图与D-InSAR地表形变场进行差分,结果如图 7、图 8所示。
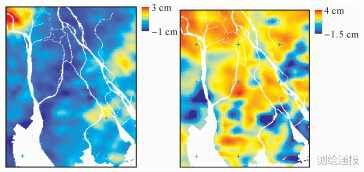 |
| 图 6 2009-12-28—2010-03-04与2010-03-04—2010-05-09整体改正后的差分大气延迟改正 |
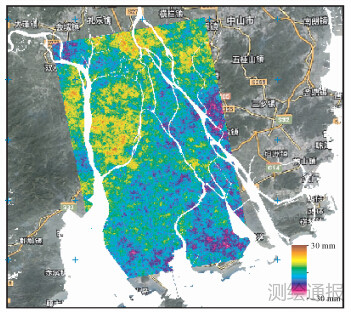 |
| 图 7 2009-12-28—2010-03-04大气延迟改正 |
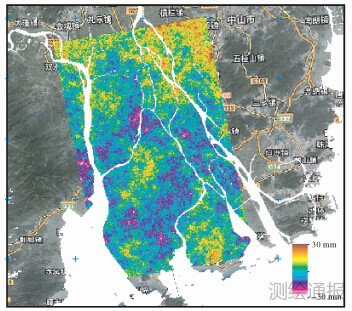 |
| 图 8 2010-03-04—2010-05-09大气延迟改正 |
试验表明,基于这一算法改正后的珠三角地表沉降量平均值分别为1.58 cm与2.2 cm,标准差分别为0.93和1.07。相对利用MODIS改正后的地表沉降平均值有所降低,表明改正效果较好。但在东北局部区域及沿海区域大气延迟改正效果一般。
将图 9大气延迟改正图应用于D-InSAR大气改正,结果如图 10、图 11所示。
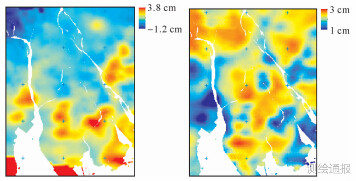 |
| 图 9 2009-12-28—2010-03-04与2010-03-04—2010-05-09局部改正后的差分大气延迟改正 |
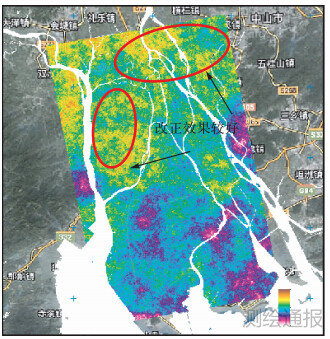 |
| 图 10 2009-12-28—2010-03-04局部纠正大气延迟改正 |
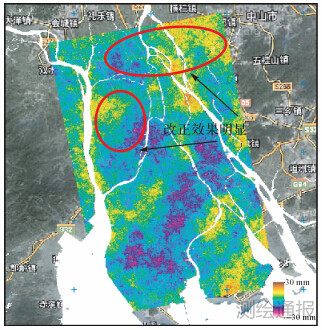 |
| 图 11 2010-03-04—2010-05-09局部纠正大气延迟改正 |
从图中干涉测量大气改正结果可以看出,相比初始监测结果,山区等大气影响较强的区域其延迟误差得到了明显削弱。整体上地表沉降量较小,在0~7 mm之间,表明形变趋势缓慢。
上述分别利用MODIS大气延迟、GPS与MODIS整体改正后的大气延迟、GPS与MODIS局部改正的大气延迟对D-InSAR形变场进行了大气改正。根据试验结果,本文统计分析了经大气改正后的沉降量变化,见表 5。
| cm | ||||||||
| 2009-12-28—2010-03-04 | 2010-03-04—2010-05-09 | |||||||
| 最小沉降量 | 最大沉降量 | 平均沉降量 | 标准差 | 最小沉降量 | 最大沉降量 | 平均沉降量 | 标准差 | |
| D-InSAR | -2.16 | 2.83 | 1.79 | 1.26 | -1.72 | 2.775 | 2.249 | 1.45 |
| MODIS | -1.12 | 1.87 | 1.23 | 1.3 | -1.89 | 2.96 | 2.77 | 1.32 |
| 整体改正 | -1.55 | 1.89 | 1.38 | 0.931 | -1.8 | 2.9 | 1.83 | 1.07 |
| 局部改正 | -1.45 | 1.67 | 0.85 | 1.03 | -1.8 | 1.6 | 1.26 | 0.87 |
为了直观地对比试验结果,本文获取了测区内均匀分布的100个样本点的数据,如图 12所示。
 |
| 图 12 样本点分布范围 |
1) GPS与MODIS整体改正结果如图 13、图 14所示。
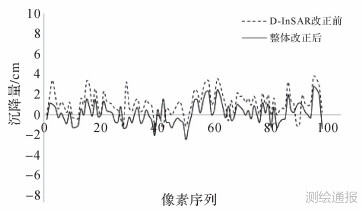 |
| 图 13 2009年12月—2010年3月大气改正结果 |
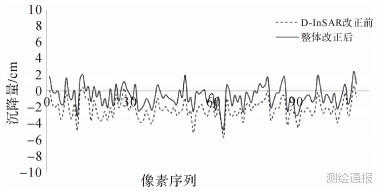 |
| 图 14 2010年3月—2010年5月大气改正结果 |
2) GPS与MODIS局部改正结果如图 15、图 16所示。
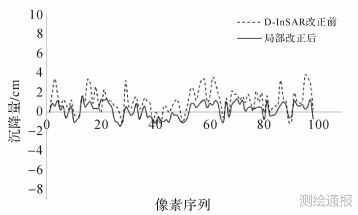 |
| 图 15 2009年12月—2010年3月大气改正结果 |
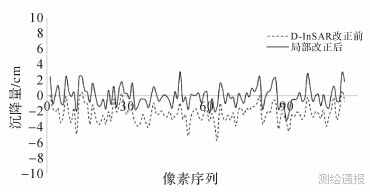 |
| 图 16 2010年3月—2010年5月大气改正结果 |
从图 13中可以看出,3种改正算法对D-InSAR大气延迟相位均有一定的削弱作用。经大气改正后的样本点沉降量更趋向于零面,总体上RMS有所降低。试验表明基于GPS与MODIS水汽数据融合从而反演精确的大气延迟改正是一种可行的方法。然而从上述结果可以看出,这并不能完全去除大气对于干涉测量的影响。改正后的地表沉降场中仍然有大气附加值,这主要受到了几个方面的影响:GPS由于高度角、测站坐标、地表加权平均温度等导致的反演天顶对流层湿延迟误差;MODIS水汽数据获取时间与SAR影像的非同步特性;对流层湿延迟转换至雷达方向的转换方程误差。
四、结束语本文研究了GPS融合MODIS水汽数据以反演D-InSAR大气延迟算法,基于同时期的GPS数据与MODIS大气数据研究分析了GPS-MODIS数据整体改正算法。在此基础上,根据大气水汽分布的时空相关性及局部特征,提出了基于空间距离加权改正的GPS-MODIS局部改正算法,并验证了其有效性。为了更好地进行大气延迟改正,需要在以下几个方面进一步开展研究:①GPS站点的同步气象观测数据:利用大气水汽计算路径湿延迟的一个关键因素是转换因子的计算。这就需要在GPS观测时同步测量地表气象数据,包括相对湿度、气压、温度等。②电离层折射影响的考虑:一般认为电离层在小区域内变化较小,通过双次差分可抵消。实际上其对SAR信号的折射率变化与空间辐射和太阳活动密切相关。因此研究电离层的电子浓度变化对改正电离层延迟影响具有重要的作用。③考虑地表高程与大气水汽分布关系:大气水汽含量及变化具有空间相关性,且与地形密切相关。因此研究顾及空间和地形分布的插值方法对表达水汽的分布机理有重要的作用。
| [1] | GOLDSTEIN R. Atmospheric Limitations to Repeat-track Radar Interferometry[J]. Geophysical Research Letters, 1995, 22(18): 2517-2520. |
| [2] | TARAYRE H, MASSONNET D. Atmospheric Propagation Heterogeneities Revealed by ERS-1 Interferometry[J]. Geophysical Research Letters, 1996, 23(9): 989-992. |
| [3] | SANDWELL D T, PRICE E J. Phase Gradient Approach to Stacking Interferograms[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1998, 103(B12): 30183-30204. |
| [4] | WILLIAMS S, BOCK Y, FANG P. Integrated Satellite Interferometry: Tropospheric Noise, GPS Estimates and Implications for Interferometric Synthetic Aperture Radar Products[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1998, 103(B11): 27051-27067. |
| [5] | WEBLEY P W, BINGLEY R M, DODSON A H, et al. Atmospheric Water Vapour Correction to InSAR Surface Motion Measurements on Mountains: Results from a Dense GPS Network on Mount Etna[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2002, 27(4): 363-370. |
| [6] | LI Z, MULLER J P, CROSS P, et al. Assessment of the Potential of MERIS Near-Infrared Water Vapour Products to Correct ASAR Interferometric Measurements[J]. International Journal of Remote Sensing, 2006, 27(2): 349-365. |
| [7] | ONN F. Modeling Water Vapor Using GPS with Application to Mitigating InSAR Atmospheric Distortions[D]. [S.l.]:Stanford University, 2006. |
| [8] | 宋小刚,李德仁,单新建,等.基于GPS和MODIS的ENVISAT ASAR数据干涉测量中大气改正研究[J].地球物理学报,2009,52(6):1457-1464. |
| [9] | 陈瑞琼, 刘娅, 李孝辉. 卫星导航系统中对流层改正模型分析[J]. 测绘通报, 2015(3): 12-15,36. |
| [10] | 张晋升,匡翠林,谢荣安,等.GPS自动变形监测软件设计与实现[J].工程勘察,2013(8):67-70. |
| [11] | 薛永安, 葛永慧. GPS变形监测数据处理管理系统的设计与实现[J]. 太原理工大学学报, 2006, 37(4):423-426. |
| [12] | 龙四春,唐涛,张赵龙,等. DInSAR集成GPS的矿山地表形变监测研究[J]. 测绘通报, 2014(11): 6-10. |
| [13] | 李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉:武汉大学出版社, 2009. |
| [14] | 焦道振, 谢荣安, 杨贤伟. 三维GIS平台的地面沉降地质灾害信息系统研究[J]. 测绘通报, 2014(11): 120-122. |