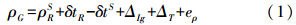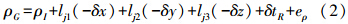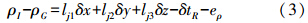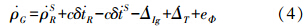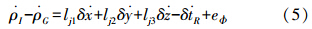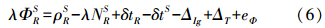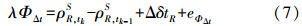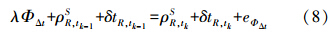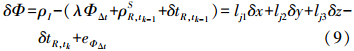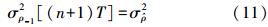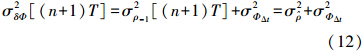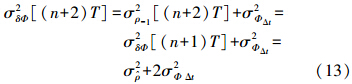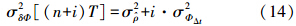一、引 言
紧组合模式直接依赖于GNSS原始观测值,相比松组合,紧组合系统可以在卫星少于4颗时工作,而且运算精度较高,速度较快[1]。传统的GNSS/INS组合系统一般利用伪距作为观测值,导航性能依赖于伪距精度。载波相位观测值精度远高于伪距,但组合导航中整周模糊度的实时解算还很困难,时间差分载波相位(time-differenced carrier phase,TDCP)则可以避免整周模糊度问题。通常,时间差分载波相位可用于导出平均多普勒[2],作为伪距率观测信息引入到紧组合观测系统中[3, 4],实际上,它可以作为原始观测值直接应用到紧组合观测系统中[5, 6]。
时间差分载波观测方程中,前后历元状态参数相关,不符合标准Kalman滤波的要求[7, 8, 9]。Wendel和Han均推导了严密的时间差分载波观测方程[10, 11],该方程以速度误差参数为媒介将状态向量融合进来,但是这种较为严密的公式计算过于复杂,影响滤波效率。Soon等认为可以直接将前一历元的信息作为已知值,采用简化方程,取得了较好的结果[12],但是该方法没有考虑前一历元信息对随机模型的影响及差分载波引起的位置误差积累问题。
本文采用简化时间差分载波观测模型,分析了此模型的误差影响,说明了短期内时间差分载波观测更新精度较高但存在误差积累问题的特点,重点推导了双周期组合情况下的时间差分载波观测值的实用随机模型确定公式,该随机模型同时顾及了长周期伪距更新的误差影响和短周期时间差分相位更新的误差叠加效应。将采用时间差分载波的组合方案与传统伪距组合方案进行比较,结果表明,时间差分载波观测值精度高,在观测随机模型可靠的情况下优于传统的伪距紧组合导航。 二、传统伪距紧组合观测模型 1. 伪距差观测模型
GNSS的伪距观测方程为
式中,ρG为伪距观测值;ρRS为星地距离;δtR为接收机钟差;δtS为卫星钟差;ΔIg和ΔT为大气折射延迟。为简洁起见,后面推导省略卫星钟差和大气折射延迟有关项。
将ρRS在INS坐标处展开,则有
式中,ρI为由INS坐标计算的伪距;δx、δy和δz为位置误差参数δR的三分量;lj为方向余弦反号。
移项整理得
ρI-ρG即为组合导航系统的伪距差观测值。2. 基于多普勒观测值的伪距率差观测模型
GNSS的伪距率通常由多普勒观测值求出,低成本接收机中也可由伪距和载波时间差分导出。
伪距率观测方程为
将INS速度值代入并整理可得伪距率差观测方程为
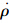 I-
I-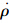 G即为伪距率差观测量。
G即为伪距率差观测量。伪距率差反映了载体的速度信息,有利于提高姿态和速度精度。因此,为更好地比较分析伪距观测值和时间差分载波相位观测值对系统定位精度的不同影响,应用多普勒观测值作为速度约束方程,即多普勒观测值分别与伪距和时间差分载波相结合。
三、时间差分载波(TDCP)观测模型
非差载波相位观测方程为
对tk和tk-1时刻的载波相位观测值做差,可消去模糊度参数。历元间作差得到时间差分载波相位(TDCP)观测方程为
式中,TDCP观测值λΦΔt=λΦSR,tk-λΦSR,tk-1;接收机钟差之差ΔδtR=δtR,tk-δtR,tk-1。
对于接收机钟差之差ΔδtR,可以在卫星间第二次作差来消去。周跳对TDCP的影响远远小于对非差观测值的影响,它只影响本历元的TCDP观测值,因此,在TDCP的组合导航系统中,周跳的影响可以忽略[11]。
式(7)所示的TDCP观测方程中同时含有前后两个历元的导航参数,无法直接应用Kalman滤波公式,使用状态延迟Kalman滤波[9]可以解决这个问题,但是这种滤波器将前后历元的参数整合成一个整体参数,极大地增加了滤波器的负担。Wendel和Han以速度误差参数为媒介将状态向量融合进来,得到一个极为复杂的严密公式,且此严密公式实际上是速度约束方程。同为速度约束方程,多普勒观测值的精度稳定性高于TDCP,在使用多普勒的情况下,不需要再使用此TDCP严密公式。
TDCP观测值主要描述用户位置的相对变化,因此,可以从应用效率的角度出发,直接将前一时刻组合导航系统的状态值作为已知值代入式(7)中,可得
式(8)在INS位置处展开,有
式中,δΦ即为GNSS/INS组合导航中的TDCP观测值。如果采用星间再作二次差,则接收机钟差相关的参数可进一步消去。
若要应用式(9),关键问题是确定δΦ的随机模型,这里不仅要考虑eΦΔt的影响,还需要考虑前一时刻参数的统计信息的影响,其中,eΦΔt的影响相对较小且比较稳定。
四、利用TDCP的组合导航系统滤波结构
TDCP观测值精度高,相对于伪距观测值能够维持组合导航系统短期内较高的精度。但是,前一时刻导航信息的误差必然会不断积累,影响系统的长期精度。这里,先分析仅用TDCP观测值时的导航性能,再给出双周期更新的滤波结构,重点推导了此滤波结构下的随机模型。
1. 仅用TDCP观测值的组合导航精度
对一组GPS/INS组合数据进行TDCP观测值与INS系统的组合,不使用伪距观测信息。将TDCP观测值组合导航结果与传统伪距观测值(这里用的C/A码)组合导航结果进行比较,组合系统位置初值为精度极高的已知点。两种组合方式2 min内的误差绝对值分别如图 1—图 3所示。
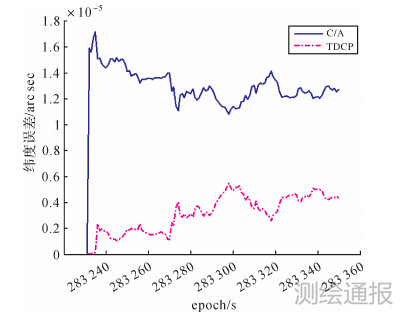 |
| 图 1 纬度误差 |
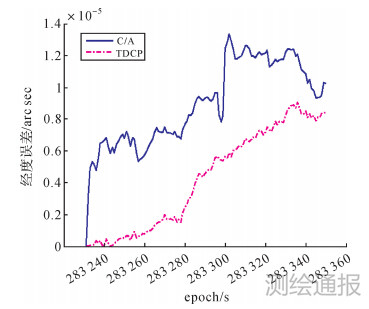 |
| 图 2 经度误差 |
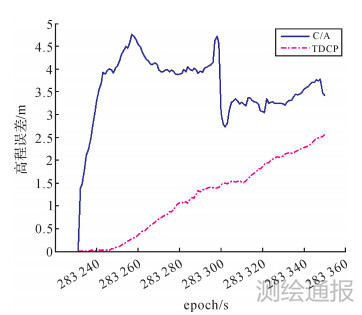 |
| 图 3 高程误差 |
传统伪距辅助的组合导航精度主要受伪距测距精度影响,由于非差伪距测量受大气折射延迟误差、卫星钟差等影响较大,组合后经纬度精度基本稳定在1.0e-5角秒量级,高程精度基本维持在4.0 m量级,此位置精度和单独使用GNSS伪距进行导航的精度相当。
使用TDCP观测值的组合系统短时间内定位精度明显高于伪距组合结果。TDCP观测值的观测误差eΦΔt经过时间差分后仅含少量残余误差成分的影响,对INS的位置约束能力更强。但是随着时间变化,前一时刻导航参数ρSR,tk-1等所含误差使得定位误差不断积累。如果仅仅使用TDCP观测值的话,导航结果在一段时间之后会发散。因此,在组合导航中对于TDCP观测值的应用关键是要在利用其短期高精度的同时抑制其误差积累。
2. 双周期更新及滤波随机模型确定方法
本文的组合更新结构是将用TDCP在各GNSS采样时刻上与INS组合的同时,利用伪距在更长的周期上进行组合,以抑制TDCP观测值的误差积累。可以从频域角度理解该组合导航系统,INS优势在高频部分,伪距优势在低频部分,而TDCP便是介于两者之间的频带。
记TDCP更新周期为T,伪距更新周期为nT,对于一段历元nT,(n+1)T,(n+2)T,…,2nT,其中nT和2nT时刻使用伪距观测模型组合INS;(n+1)T,(n+2)T,…,(2n-1)T时刻使用TDCP观测模型组合。对于任一时刻的TDCP观测值δΦ,其误差影响包含两个部分
式中,σ2ρ-1代表前一时刻状态参数估计误差所引起的等效距离误差;σ2ΦΔt为误差项eΦΔt的方差。
对于(n+1)T时刻,σ2ρ-1为nT时刻伪距更新结果的等效距离误差,即
则有
对于(n+2)T时刻,σ2ρ-1即为(n+1)T时刻的误差,即
显然,(n+i)T时刻的误差为
式(14)即为滤波更新过程中TDCP观测方程的随机模型确定公式。值得指出的是,σp2虽为伪距观测值更新时刻计算所得的导航参数等效距离误差,但不同于传统单纯使用伪距组合导航时的距离误差,因为组合导航滤波实际上是一个两种导航系统不断互补的结果,是前面所有历史信息的总和,伪距更新周期内的TDCP更新贡献很大。
五、计算与分析
采用一组战术级GPS/INS试验数据,IMU采样频率为100 Hz,GPS采样频率为1 Hz,对GPS/INS数据进行紧组合解算。以载波相位差分获得的位置作为参考解。分别采用如下两种方案进行紧组合导航解算:
方案1:使用传统伪距观测值更新的紧组合算法。
方案2:使用TDCP短周期结合伪距长周期更新的紧组合算法。
在方案2中,TDCP观测值的更新周期为1 s,伪距观测值的更新周期为30 s,采用第4章第2节的方法确定观测值随机模型。两种方案的三方向误差结果(绝对值)分别如图 4—6所示,RMS比较见表 1。
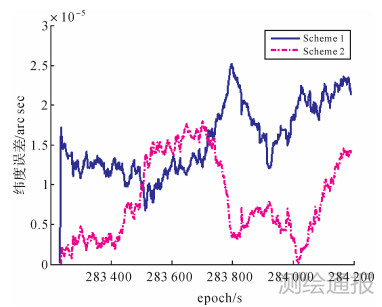 |
| 图 4 两种方案的纬度误差 |
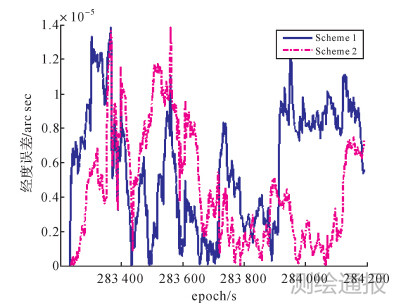 |
| 图 5 两种方案的经度误差 |
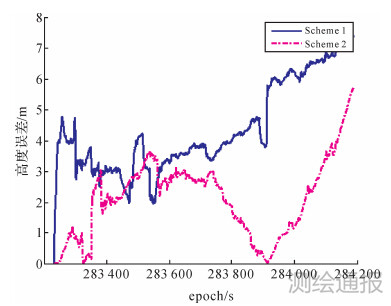 |
| 图 6 两种方案的高度误差 |
| 纬度/arc sec | 经度/arc sec | 高程/m | |
| 方案1 | 1.614e-005 | 0.684e-005 | 4.634 |
| 方案2 | 0.959e-005 | 0.561e-005 | 2.465 |
通过上述计算结果,可以得出结论:
1) 本文利用TDCP的组合导航方案优于传统利用伪距的组合导航方案。TDCP观测值削弱了多种误差成分,在每一段短时间的更新周期内能更好地维持组合系统的精度。因为避免了模糊度解算问题,其效率与传统伪距方法相当。
2) 使用TDCP和伪距双周期更新的紧组合系统相比传统伪距组合在各方向上精度分别提高41%、18%和47%,其中误差最大的高程方向改善最为明显,时间差分对误差的削弱效果明显。
六、结束语
时间差分载波相位避免了整周模糊度解算问题,并减小了周跳的影响范围,其对卫星钟差和大气折射延迟等误差的削弱作用明显,具有短期精度高的特点。
时间差分载波本质上属于相对测距,其误差随时间积累,利用伪距在更大的周期上组合能同时发挥时间差分载波和伪距在不同频带上的优势,提高导航精度。在简化的时间差分载波相位观测模型基础上,本文推导了双周期更新滤波结构下的随机模型,并应用于组合导航实际数据处理中。相对于传统伪距组合,利用载波相位时间差分的双周期更新滤波在经度和纬度方向的精度分别提高41%和18%,而在误差最大的高程方向,则高达47%。
| [1] | 柴艳菊. 挖掘信息提高GPS/INS导航精度的理论与方法研究所[D]. 武汉: 中国科学院测量与地球物理研究所, 2008. |
| [2] | 何海波, 杨元喜, 孙中苗. 几种GPS测速方法的比较分析[J]. 测绘学报, 2002, 31(3): 217-221. |
| [3] | 吴富梅, 秦显平, 唐颖哲. 低成本车载GPS/INS组合导航速度更新算法[J]. 测绘科学技术学报, 2010, 27(4): 243-246. |
| [4] | MOAFIPOOR S, GREJNER-BRZEZINSKA D A, TOTH C K. Tightly Coupled GPS/INS Integration Based on GPS Carrier Phase Velocity Update [C]//ION NTM 2004. San Diego CA: [s.n.], 2004: 1094-1102. |
| [5] | 汤勇刚, 练军想, 吴文启, 等. 北斗载波相位时间差分/SINS紧组合技术与实验研究[J]. 国防科技大学学报, 2007, 29(2): 19-23. |
| [6] | 温永智, 吴杰. 高轨飞行器精确导航的载波相位时间差分/捷联惯导紧组合算法[J]. 武汉大学学报:信息科学版, 2011, 36(10): 1195-1199. |
| [7] | FARRELL J L. GPS/INS-streamlined[J]. Navigation, 2002, 49(4): 171-182. |
| [8] | VAN GRASS F, FARRELL J L. GPS/INS-a Very Different Way [C]//ION 57th Annual Meeting/CIGTF 20th Biennial Guidance Test Symposium. Albuquerque NM: [s.n.], 2001: 715-721. |
| [9] | FORD T J, HAMILTON J. A New Positioning Filter: Phase Smoothing in the Position Domain [J]. Navigation, 2003, 50(2): 65-78. |
| [10] | WENDEL J, TROMMER G F. Tightly Coupled GPS/INS Integration for Missile Applications[J]. Aerospace Science and Technology, 2004, 8(7): 627-634. |
| [11] | HAN S L, WANG J L. Integrated GPS/INS Navigation System with Dual-Rate Kalman Filter [J]. GPS Solution, 2012, 16(3): 389-404. |
| [12] | SOON B K H, SCHEDING S, LEE H K, et al. Performance Analysis of an Integrated Navigation System In Urban Canyon Environment [C]//IGNSS Symposium 2007. Sydney, Australia: [s.n.], 2007. |