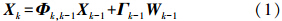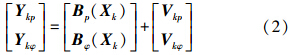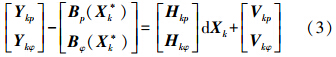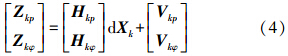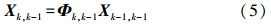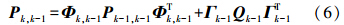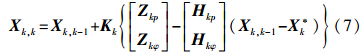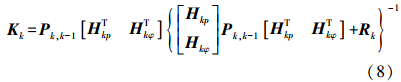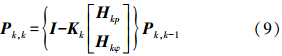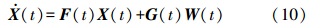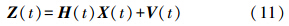,
一、引 言
全球卫星导航系统(global navigation satellite system,GNSS)和惯性导航系统(inertial navigation system,INS)具有良好的互补特性，因此GNSS/INS组合成为组合导航领域主要的组合方法。目前应用最广泛的是基于伪距的组合，但是其定位精度只能达到米级，尚不能满足对于厘米级甚至更高精度的位置姿态系统(positioning and orientation system，POS)的要求。POS系统广泛应用于遥感[1]、车载移动测图[2]、国家基础测绘、城市规划、国土资源管理[3, 4]等方面，它充分利用了载波相位信息与惯导组合来获取载体的位置和姿态信息，高精度的数据处理算法是POS系统的核心技术之一[5]。
本文首先介绍了POS系统数据处理的流程，利用双卡尔曼滤波器进行整周模糊度的估计与误差修正量的计算；其次对基于载波相位观测量的紧组合卡尔曼滤波模型进行了分析，列出了其状态方程和量测方程；最后通过实测数据验证了该算法的精度，并与高精度GNSS/INS数据处理软件IE(Inertial Explore)的后处理结果进行了比较。
二、数据处理流程
整个系统数据的采集主要通过惯性测量单元(inertial measurement unit，IMU)、基站GNSS接收机及移动站GNSS接收机3部分获得，如图 1所示。IMU可实时测量载体的角速度及加速度信息，通过解算获得载体的位置速度和姿态等全部运动参数，但是其误差随时间积累，GPS利用载波相位信息可以得到高精度的位置和速度，但是信号容易受到遮挡和干扰，因此POS系统中常常将二者组合起来实现优势互补[6]。在数据处理方面，为了减小矩阵的维数便于计算，不采用附加模糊度参数的集中卡尔曼滤波器，而是利用两个分散的滤波器共同完成[7]。其中主卡尔曼滤波器用于状态参数的估计，对惯导计算出来的导航结果及惯性器件误差进行闭环修正，次卡尔曼滤波用来对模糊度的浮点解及其协方差阵进行估计；同时利用惯导输出的位置信息，提高模糊度浮点解的精度和缩小搜索范围，LAMBDA用来完成模糊度的搜索，将固定之后的整数模糊度代入主卡尔曼滤波器中，完成参数的估计过程。
 |
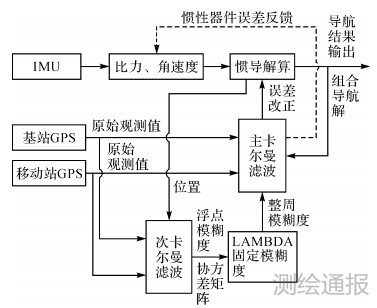| 图 1 数据处理流程 |
由于主卡尔曼滤波需要用到次卡尔曼滤波的整周模糊度信息，因此首先介绍次卡尔曼滤波的状态方程和量测方程。
1. 次卡尔曼滤波器
次卡尔曼滤波器完成浮点模糊度及其协方差矩阵的估计，状态向量为Xk=[xkykzkΔ∇N12Δ∇N13…Δ∇N1n]T，其中，(xk,yk,zk)为移动站位置估计，Δ∇N为双差载波相位整周模糊度，n为共视卫星数，状态向量中包括n－1个整周模糊度参数[8]。
滤波器的状态方程为
式中
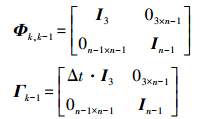
Wk－1为系统噪声协方差矩阵。
滤波器的量测方程为
式(2)为非线性方程，令其在近似值Xk*处线性化，可得线性化观测方程
或记为
式中，Zkp=Ykp－Bp(Xk*)；Zkφ=Ykφ－Bφ(Xk*)；Ykp为移动站双差伪距观测量；Ykφ为移动站双差载波相位观测量；Bp(Xk*)为近似值处几何双差伪距计算量；Bφ(Xk*)为近似值处几何双差载波相位计算量。
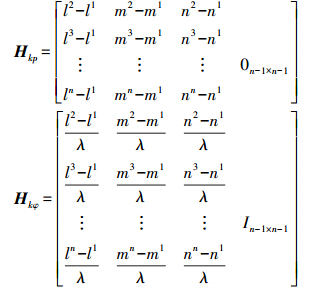
为第i颗卫星坐标；ρi*为第i颗卫星与近似值处的几何距离。
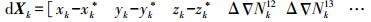
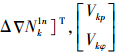设为零均值白噪声，若伪距、载波相位方差分别为σp2，σφ2，且伪距、载波相位观测值不相关，则量测噪声协方差阵为
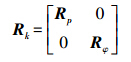
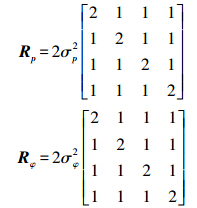
整个滤波器的递推方程为
首先设定初值，通过递推求出每个历元整周模糊度浮点解及其协方差矩阵，然后经过LAMBDA算法固定整周模糊度，同时也可以求出移动站位置。
2. 主卡尔曼滤波器
主卡尔曼滤波器采用双差紧组合的模式来完成状态变量的估计，设状态变量Xk=[φn δvn δrn bgb bab]T，其中，φn为姿态角误差矢量，δrn为速度误差矢量，δrn为位置误差矢量，bgb为陀螺仪常值零偏矢量，bab为加速度计常值零偏矢量。在当地水平坐标系下，系统状态方程即为INS的误差状态方程
式(10)中各参数矩阵的设计参考文献[9]。
利用次卡尔曼滤波器求出整周模糊度后，就可将其代入双差载波相位观测方程，形成主卡尔曼滤波器的量测方程
式中
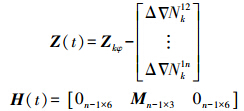
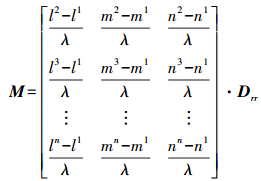
Drr为ECEF坐标系转换为当地水平坐标系的误差转换矩阵，因为状态方程的状态变量为当地水平坐标系下的，而双差载波相位观测方程的误差是ECEF坐标系下的，因此需要乘以一个转换矩阵Drr，其具体计算公式可参考文献[9]；V(t)为量测误差。
经过卡尔曼滤波的递推计算，即可估计出移动站的位置、速度和姿态信息。
四、算例分析
为验证本文所提算法的精度，采用一组实测的跑车试验数据，其中陀螺仪的零偏为0.75 deg/h，加速度计的零偏为1 mg，整个系统采用基准站加流动站的工作模式，图 2为跑车运行轨迹路线，图 3为整个运动过程中基准站和流动站的共视卫星数。
 |
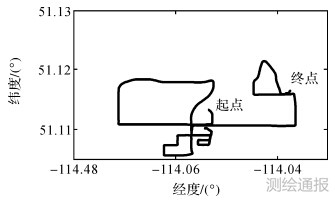| 图 2 跑车运行轨迹 |
 |
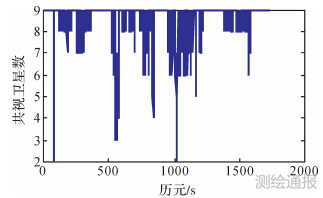| 图 3 共视卫星数 |
由于跑车路线位于市区，高楼林立，遮挡情况比较严重，可视卫星数变化剧烈，个别时刻只有2～3颗可见星，给模糊度的固定带来一定的困难，直接影响导航解算的精度。为验证本文所提算法的效果，以Inertial Explore 8.4软件的解算结果作为参考值，利用本文所述算法解算出来的位置、速度及姿态误差如图 4—图 6所示，误差的统计结果见表 1。
 |
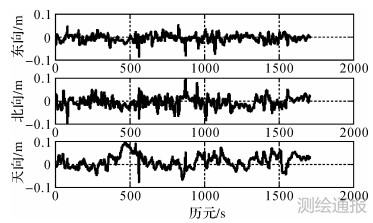| 图 4 位置误差 |
 |
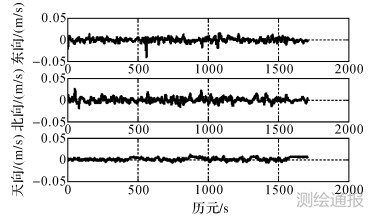| 图 5 速度误差 |
 |
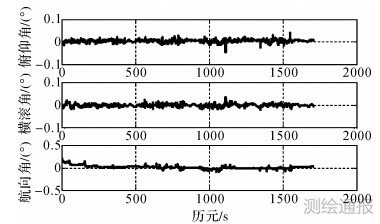| 图 6 姿态误差 |
| 平均值 | 标准差 | RMS | 最大值 | ||
| 位置/m | 东向 | -0.005 3 | 0.015 1 | 0.016 0 | 0.050 2 |
| 北向 | -0.006 3 | 0.022 0 | 0.022 9 | 0.113 3 | |
| 天向 | 0.014 8 | 0.028 5 | 0.032 1 | 0.099 0 | |
| 速度/(m/s) | 东向 | -0.000 4 | 0.004 5 | 0.004 5 | 0.015 0 |
| 北向 | -0.000 1 | 0.005 2 | 0.005 2 | 0.025 0 | |
| 天向 | 0.002 2 | 0.003 1 | 0.003 8 | 0.012 0 | |
| 姿态/(°) | 俯仰角 | 0.005 4 | 0.005 8 | 0.008 0 | 0.042 0 |
| 横滚角 | -0.000 5 | 0.005 6 | 0.005 6 | 0.034 0 | |
| 航向角 | 0.018 6 | 0.035 5 | 0.040 1 | 0.220 0 |
从图 4—图 6误差曲线及表 1的误差统计结果可以看出，在观测条件好、可视卫星数较多的情况下，利用本文所述的双卡尔曼滤波算法，可以取得较好的位置、速度及姿态精度，其中位置误差的RMS值优于4 cm，速度误差RMS值不大于5 mm/s,俯仰和横滚角RMS值小于0.008°，航向角误差的RMS值为0.04°，这主要是因为航向角的可观测性较差。虽然个别时刻观测卫星数较少，但是由于在解算时采取了紧组合的模式，对解算结果的精度影响不大，充分说明了紧组合模式的优越性。
五、结束语
充分利用载波相位信息并正确解算模糊度是获得高精度POS系统的关键，本文通过双卡尔曼滤波器实现了模糊度的解算和导航参数误差的估计，解决了单卡尔曼滤波解算由于参数多带来的稳定性问题，详细论述了每个滤波器状态方程与量测方程的建立过程，利用实测数据将该算法与高精度数据后处理软件IE的处理结果进行了比较。结果表明，该方法能够达到较高的定位、定姿及测速精度，充分证明本文提出的算法是一种高精度的数据处理方法。
| [1] | 李斐, 束蝉方, 陈武. 遥感技术中GPS/INS组合系统的应用[J]. 测绘通报, 2004(12): 1-4. |
| [2] | 陈允芳, 叶泽田. 基于多传感器融合的车载移动测图系统研究[J]. 测绘通报, 2007(1): 5-7, 19. |
| [3] | DE AGOSTINO M, PORPORATO C. Development of an Italian Low Cost GNSS/INS System Universally Suitable for Mobile Mapping[C]//2008 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA: IEEE, 2008: 53-59. |
| [4] | EI-SHEIMY N. The Development of VISAT-A Mobile Survey System for GIS Applications[D]. Calgary: University of Calgary, 1996: 13-18. |
| [5] | 邱宏波, 周东灵, 李文耀, 等. 基于闭环误差控制器的高精度POS后处理算法[J]. 中国惯性技术学报, 2010, 18(6): 691-695. |
| [6] | 房建成, 杨胜, 刘百奇. 高性能POS及其在移动测图系统中的应用[J]. 红外与激光工程, 2007, 36(S0): 478-482. |
| [7] | 孙红星. 差分GPS/INS组合定位定姿及其在MMS中的应用[D]. 武汉: 武汉大学, 2004: 95-98. |
| [8] | 刘基余. GPS卫星导航定位原理与方法[M]. 北京: 科学出版社, 2003: 289-292. |
| [9] | 苗岳旺. SINS/GPS组合导航数据处理方法研究[D]. 郑州: 信息工程大学, 2013. |