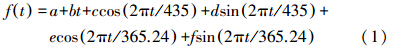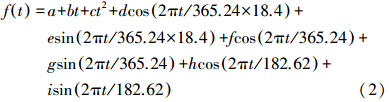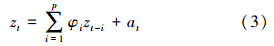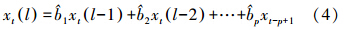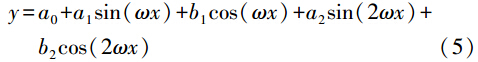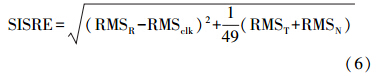一、引 言
TTFF(time to first fix)指GPS接收机开机启动后首次定位所用时间,是衡量GPS接收机性能的一个重要指标,一般来说广播星历搜集时间可占TTFF的73%[1, 2]。冷启动时,用户接收一组完整的导航电文需12.5 min[3],理想情况下(热启动且卫星通视良好)也需要18 s才能完整下载广播星历,当用户处于街道或室内等复杂环境下,卫星信号的搜索及解调将受阻,若有信息未成功完整下载,就得再重复30 s的子帧下载过程。若能预先提供广播星历,则可使TTFF由几分钟减至几秒钟,并提高接收终端灵敏度,减少功耗。在这一市场诉求下,A-GPS(assisted- Global Positioning System)技术应运而生。A-GPS技术主要以两种方式提供辅助信息:一种是即时性的连线模式(Online A-GPS),即通过GSM、GPRS、CDMA或UMTS等无线通信网络来传输辅助数据;另一种是离线模式(Offline A-GPS),即依使用者的方便预先下载卫星资料,当需要时就能使用其辅助定位。然而,Online模式容易因无线网络速率、移动运营商的服务品质及用户所在位置而影响连线效率,且受限于移动运营商的管理,这些对于用户都是不可控因素。采用Offline模式,用户只需预先在移动终端下载并保存卫星轨道资料,没有网络时即可使用其辅助定位,从而减短TTFF,也节省了网络传输费用。
由于Offline的轨道资料必须具有长期有效性,因此移动终端需具备专业的卫星轨道预测能力。本文针对GPS系统,给出了一种适用于移动终端的自主轨道预报方法,并对基于广播星历的卫星轨道预报方法与模型、EOP参数的长期预报、精化光压模型等关键问题进行了分析与测试。
二、基于广播星历的轨道预报方法
移动终端使用广播星历实现自主轨道预报的基本思路可描述为:利用终端已收集的广播星历计算一组有效时间内的卫星位置时间序列,并将其转换至惯性系,使用动力学轨道拟合方法[4]估计出拟合弧段的精确卫星初始轨道参数和力模型参数,再使用轨道积分进行外推,并将外推结果转换至地固系下生成预报轨道,以广播星历的形式供移动用户使用。该方法的优点是不需要移动网络支持,使移动用户在失去A-GPS支持及弱信号情况下可以充分使用已有观测资料,实时、快速地实现GPS卫星轨道预报。然而,该方法存在以下难点:①已知信息仅有终端存储的广播星历,原始数据精度不高;②在自主轨道预报过程中需要使用地球自转参数(earth orientation parameters,EOP),由于没有网络及其他辅助数据的支持,移动终端需具备自主预报长期EOP参数的能力。因移动终端系统资源与计算能力十分有限,为了尽可能减少系统资源的占用,缩短轨道预报耗时,需合理简化力模型,获得精确的初始轨道参数及力模型参数,以保证轨道长期预报的精度。本文将分别对基于广播星历的轨道预报方法与模型、EOP参数的长期预报、精化光压模型等关键问题进行讨论与分析。
1. 轨道预报方法与力模型
基于广播星历精确估计初始轨道状态的具体流程如下:
1) 使用收集的广播星历,计算有效时长内的卫星位置时间序列[3, 5],并将其由地固系转换至惯性系下。
2) 初始化卫星状态向量。卫星状态向量包括初始轨道参数(卫星位置、速度)及力模型参数。其中,初始轨道参数可直接通过广播星历计算获得,也可使用卫星位置时间序列内插得到,笔者使用everett方法[6]对卫星位置时间序列进行内插获得初始轨道参数;因太阳辐射压摄动是影响高轨卫星轨道确定的最大误差项,需准确估计,本文将动力学模型参数选为BERN(ECOM)光压模型的5个光压参数[7, 8, 9],可设为待估参数与初始轨道参数一起估计,也可采用精化模型来固定,笔者将对这两种方法分别进行测试与分析。本文初始化卫星状态向量时光压参数设为0。
3) 用Runge-Kutta-Fehlberg方法(RKF6(7))单步起算后,采用基于Adams方法的预报-校正算法,将轨道从初始时刻外推至末尾历元时刻,获得参考轨道及其对各动力学参数的偏导数,联合惯性系下的卫星位置坐标序列观测值,建立观测方程与法方程。
4) 解得初始轨道状态改正量。
5) 更新初始轨道状态,循环步骤3)—4),求解精确的初始轨道状态参数。
需要说明的是,对于移动用户来说,终端系统资源与计算能力有限,为了尽可能减少系统资源的占用,缩短定位时间,需对卫星摄动力模型进行合理简化。对于MEO(medium earth orbit)卫星,在仅考虑量级大于10-11km/s2力的条件下,除中心引力外,主要受到地球非球形引力、日月引力和太阳光压等摄动力的影响。大气阻力对于中高轨卫星的影响可以不顾及,地球反照摄动、潮汐摄动、相对论效应及其他第3体引力摄动基本都在10-15~10-12km/s2量级[9]。本文构造的卫星运动方程所重点考虑的力及其模型见表 1。
因轨道预报过程涉及地固系与惯性系的相互转换,此过程需使用地球定向参数EOP。考虑到在无外部辅助数据的支持下,移动终端需具备自主预报长期EOP参数的能力,本文使用文献[10]提出的基于LS+AR模型进行EOP长期预报的方法,具体实现如下:
以2年的EOPC04序列为原始数据,因AR模型要求观测时间序列平稳、正态、零均值,为满足后期建模的需求,需对原始序列进行预处理:首先去除UT1-UTC序列中的跳秒、固体地球带谐潮汐项和季节性变化项,以及LOD序列中固体地球带谐潮汐项等,然后将极移序列和经过上述改正的UT1-UTC序列、LOD序列分别进行差分,获得平稳的差分时间序列。
对差分时间序列进行LS拟合。其中,对X方向极移和Y方向极移的LS拟合,主要考虑极移的长期线性趋势项、Chandler摆动项和年周期项,拟合模型如式(1)所示;对UT1-UTC及LOD的LS拟合,主要考虑线性项、18.4年项、周年项和半年项,拟合模型如式(2)所示。
式中,t为时间;a、b、c、d、e、f、g、h、i为待估参数。LS预测之后,去除极移、UT1-UTC及LOD序列中的趋势项和周期项,获得各自的残差序列并对极移的残差序列进行差分,获得平稳的新序列,对其建立AR模型 式中,zt(t=1,2,…,N)为EOP参数残差序列值;a为零均值白噪声;p为阶数;φ1,φ2,…,φp为自回归系数。其中,最佳阶数p可以通过 Akaike最终预测误差(final prediction error,FPE)准则来确定,自回归系数可以通过解Yule-Walker方程获得[11]。求得模型阶数和系数后,即可根据下式对EOP参数进行预报。 式中,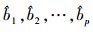 为已确定的回归系数;l 为预报步长,即天数。
为已确定的回归系数;l 为预报步长,即天数。得到所需天数的残差预报值之后,将其恢复为非差分值,并对UT1-UTC和LOD项依次加入季节性改正项、固体地球带谐潮汐项、跳秒等改正值,即可得到所需的EOP预测值。 3. 精化光压模型参数
太阳辐射压摄动是影响高轨卫星轨道确定的最大误差源[7],因此高精度的光压参数是实现高精度轨道预报的重要因素。本文采用BERN(ECOM)光压模型,模型参数 D、Y、B、BC、BS可以作为待估参数通过动力学轨道拟合来估计,也可以在预报轨道时固定一组光压参数。固定光压参数的方法是根据较长时间(如几年)的事后精密星历,通过动力学方法获得每颗卫星的BERN(ECOM)光压模型五参数,采用二阶傅里叶多项式对这些模型参数进行拟合[8],即
获得系数a0、a1、b1、a2、b2、ω后,再使用式(5)预报光压模型参数,供轨道预报使用。此方法的优点是利用了光压模型参数的长期变化规律,能够有效提高卫星轨道面定向参数(Ω和i)的长期预报精度,使太阳光压模型参数预报值更为准确合理[8]。三、算例分析
因轨道预报精度与拟合时长和光压参数强相关,本文分别以1、2、3、4、5、6、7、8、9、10、11、12 d为拟合时长,分析在不同的光压参数处理策略下,第1、7、14 d预报轨道的精度(如图 1所示)。不同拟合时长所对应的拟合弧段及预报弧段见表 2,详细的轨道预报光压参数方案见表 3。
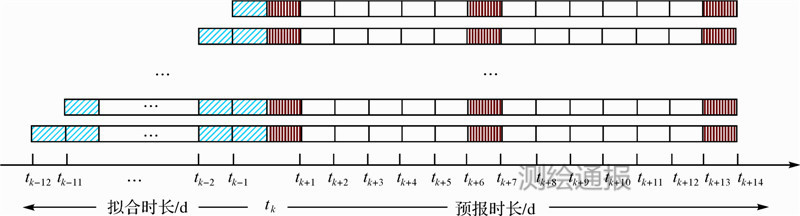 |
| 图 1 轨道预报示意图 |
| 拟合时长 /d | 拟合 弧段1 | 拟合 弧段2 | 拟合 弧段3 | … | 拟合 弧段14 |
| 1 | 110 | 111 | 112 | … | 123 |
| 2 | 109—110 | 110—111 | 111—112 | … | 122—123 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| 11 | 100—110 | 101—111 | 102—112 | … | 113—123 |
| 12 | 099—110 | 100—111 | 101—112 | … | 112—123 |
| 预报弧段 | 111—124 | 112—125 | 113—126 | … | 124—137 |
根据表 2和表 3获得每种方案在不同拟合时长下的预报轨道后,以预报时段的事后IGS精密轨道为真值与预报轨道比较,将轨道差值转换至卫星轨道坐标系(RTN坐标系),并统计每颗卫星每天的径向(R)、切向(T)、法向(N)轨道误差RMS,以及系统所有卫星的平均RMS。因每个方向误差影响不同,本文使用SISRE(signal-in-space range error)来评价预报轨道的整体精度,其表达式为[3]
式中,RMSR、RMST、RMSN分别表示径向、切向、法向的轨道误差;RMSclk为卫星钟差(本文中为0),其统计结果可直接反映整个系统预报轨道的精度。结合表 2和表 3,一种光压参数方案对应12种拟合时长方案,则共有48种处理策略,且每种策略均有14个样本,对这14个样本的预报轨道结果统计SISRE并求取平均值,则可获得每种处理策略的综合平均值。图 2给出了不同处理策略下预报第1 d、第7 d、第14 d的SISRE。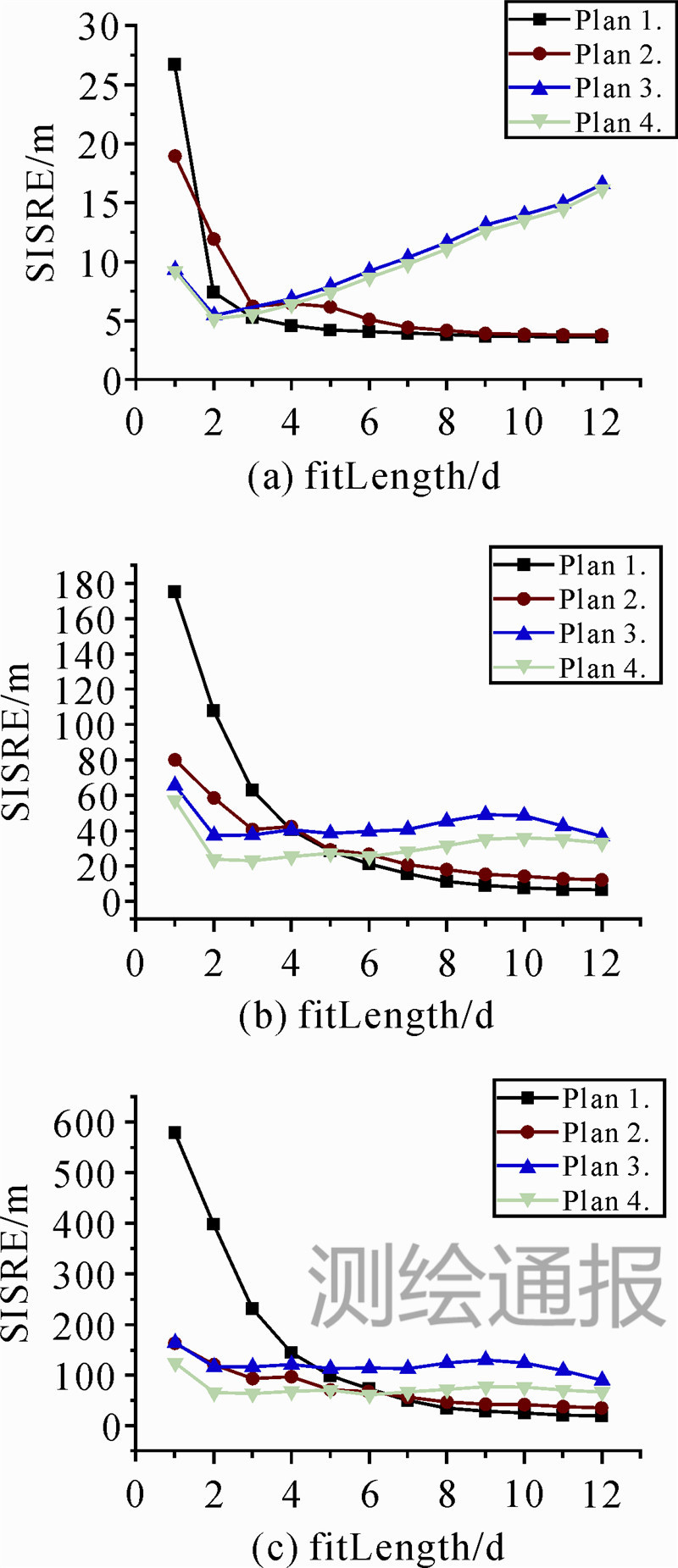 |
| 图 2 不同策略预报第1 d、7 d、14 d的SISRE注:图(a)为第1 d预报结果,图(b)为第7 d预报结果,图(c)为第14 d预报结果 |
根据图 2,从轨道精度随拟合时长的变化和光压参数的选择来分析,采用方案1和方案2进行轨道预报,其预报精度随拟合时长的增加有明显提升,这主要是因为增加轨道拟合弧长使初始轨道参数和光压参数的估计更加精确,但当广播星历弧长达8 d以上时,精度改善趋向稳定。然而,这两种方案的预报轨道精度随拟合时长、预报时长的变化程度是具有差异的,在拟合时长较短的情况下,方案2的预报轨道精度优于方案1,但随着拟合时长的增加,方案1将优于方案2,并且两种方案预报轨道精度差异的分界点(交叉点)随着预报时长的增加而后移,这主要是由于不同拟合时长条件下,轨道初始状态参数和光压参数的改进对改善轨道预报的主导作用不同而引起的。
比较方案3与方案4的轨道预报结果,当拟合弧长在3 d以内时,其预报轨道精度均明显优于方案1和方案2,这是因为在拟合弧长较短时(3 d以内)没有足够的原始数据,方案3、方案4轨道拟合仅估计6个初始轨道参数(位置、速度),减少了估计参数个数,提高了解的精度;当拟合时长增加至3 d以上,短期预报轨道精度迅速衰减,这说明增加拟合时长对改善初始轨道参数影响有限;另外在预报时,方案3没有引入光压摄动改正,而方案4使用了精化光压模型参数,故中长期预报结果优于方案3。
综上,可根据移动终端实际储存的广播星历弧长,制定不同的预报策略。为节省移动终端系统资源,给出如下建议:将终端存储的广播星历弧长控制在最近8 d以内,不同拟合弧长条件下的最佳光压参数方案见表 4,此方案统计结果如图 3所示。
| 拟合弧段 长度/d | 预报弧段 长度 | 轨道拟合 | 轨道预报 |
| 1~2 | 14 d | 不估计,设为0 | 精化模型固定 |
| 3~4 | 3 d以内 | 估计 | 轨道拟合估计值 |
| 4 d以上 | 不估计,设为0 | 精化模型固定 | |
| 5 | 7 d以内 | 估计 | 轨道拟合估计值 |
| 8 d以上 | 不估计,设为0 | 精化模型固定 | |
| 6~8 | 14 d | 估计 | 轨道拟合估计值 |
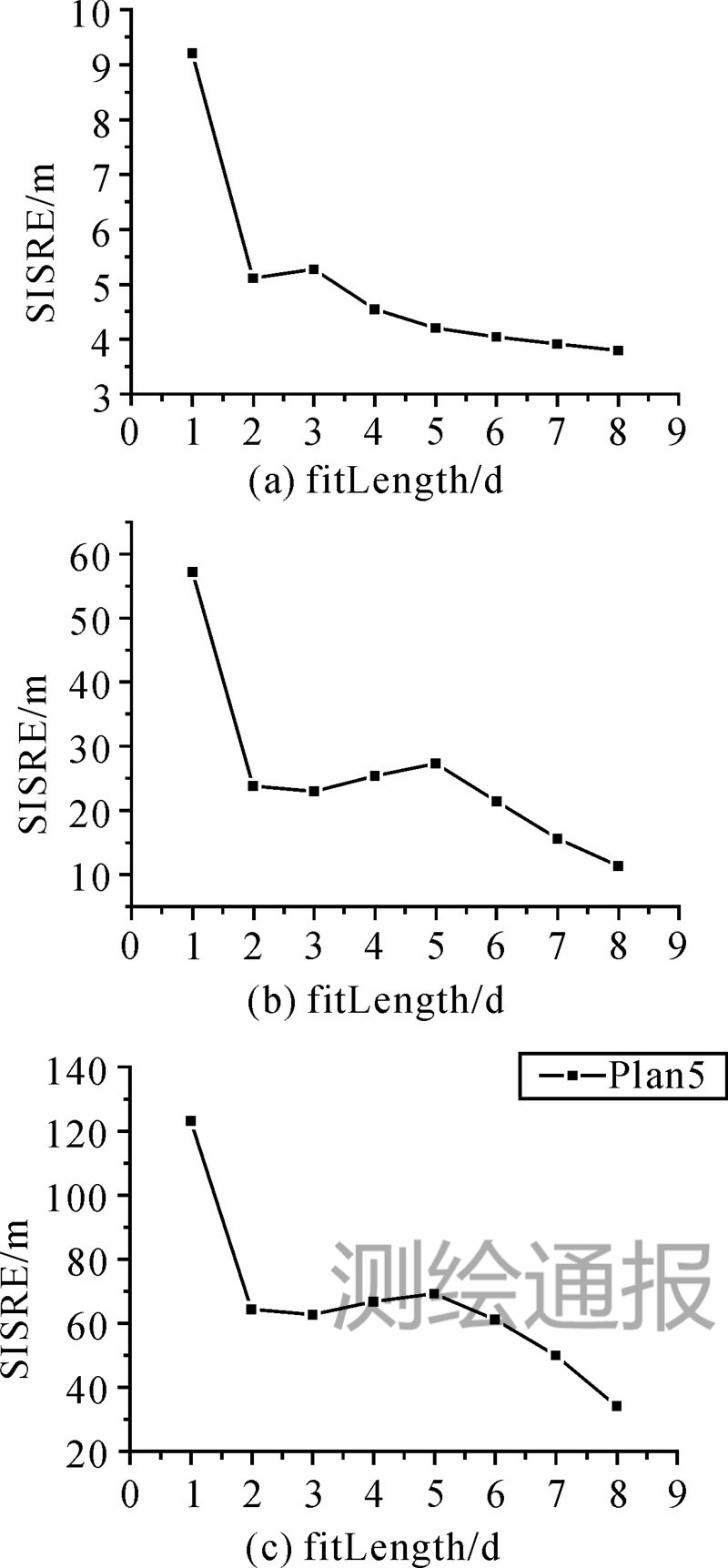 |
| 图 3 使用最佳方案(Plan5)预报第1 d、7 d、14 d的SISRE注:图(a)为第1d预报结果,图(b)为第7d预报结果,图(c)为第14d预报结果 |
根据此建议,当拟合时长仅有1 d时,可使预报1 d、7 d、14 d的SISRE分别在10 m以内、57 m左右和120 m左右;当拟合时长在2~6 d时,可使预报1 d、7 d、14 d的SISRE分别降至5 m、23 m和64 m左右;若拟合时长保持在6~8 d,可使预报1 d、7 d、14 d的SISRE分别达3 m、15 m及30 m左右。
四、结束语
本文给出了一种基于移动终端广播星历的GPS卫星轨道预报方法,并对移动终端轨道预报方法与简化力模型参数、EOP参数的长期预报、精化光压模型等关键问题进行了分析。实测数据计算的结果表明,将用于生成扩展星历的陈旧广播星历弧段控制在最近8 d以内,若广播星历弧长不足3 d,在轨道拟合时则不估计光压参数,但在轨道预报时使用精化光压模型参数进行外推;若广播星历有3~4 d弧段,可在轨道拟合时同时估计初始轨道参数与光压参数以进行3 d以内的短期预报,对于4 d以上的预报,则可在轨道拟合时仅估计初始轨道参数,而外推时使用精化光压模型参数;若广播星历有5 d弧段,则在轨道拟合时同时估计初始轨道参数和光压参数,以进行7 d以内的短期预报,对于7 d以上的中长期预报,则在轨道拟合时仅估计初始轨道参数,使用精化光压模型参数外推;若广播星历弧长达6~8 d,在轨道拟合时同时估计初始轨道参数和光压参数并基于此进行预报。
| [1] | RAO V, LACHAPELLE G. Propsed Single Frequency Signal Design for Optimal TTFF in IRNSS[C]//NAVCOM 2012 Pearl Jubilee International Conference on Navigation and Communication. Hyderabad: [s.n.], 2012. |
| [2] | SEPPÄNEN M, PERÄLÄ T, PICHé R. Autonomous Satellite Orbit Prediction[C]//Proceedings of the Institute of Navigation 2011 International Technical Meeting. San Diego: [s.n.], 2011. |
| [3] | 黄劲松. GPS测量原理与数据处理[M]. 武汉: 武汉大学出版社, 2005. |
| [4] | 常志巧. 利用非差观测量确定GPS 卫星轨道的方法研究[D]. 郑州: 信息工程大学, 2006. |
| [5] | 李显, 吴美平, 张开东, 等. 导航卫星速度和加速度的计算方法及精度分析[J]. 测绘学报, 2012, 41(6): 816-824. |
| [6] | 葛茂荣, 刘经南. 改进后的EVERETT差值方法[J]. 武测科技, 1994(4): 18-20. |
| [7] | 陈俊平, 王解先. GPS定轨中的太阳辐射压模型[J]. 天文学报, 2006, 47(3): 310-319. |
| [8] | 张卫星, 刘万科, 龚晓颖, 等. 导航卫星自主定轨中光压模型精化方法及其影响研究[J]. 武汉大学学报: 信息科学版, 2013, 38(6): 700-704. |
| [9] | 刘万科. 导航卫星自主定轨及星地联合定轨的方法研究和模拟计算[D]. 武汉: 武汉大学, 2008. |
| [10] | 柳文明, 李峥嵘, 刘文祥, 等. EOP预报误差及对导航卫星轨道预报的影响分析[J]. 全球定位系统, 2009(6):17-22. |
| [11] | BROCKWELL P J, DAVIS R A. Introduction to Time Series and Forecasting[M]. New York: Springer, 1996: 420. |