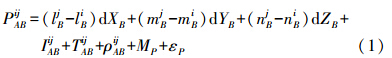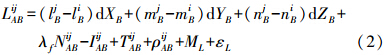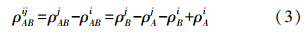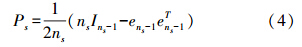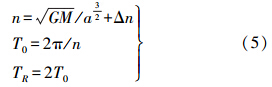2. 同济大学,上海 200092
一、引 言
北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是中国自行研制的继美国全球定位系统(GPS)和俄罗斯GLONASS之后第3个成熟的卫星导航系统[1]。2012年底第13、14号卫星的成功运行标志着覆盖亚太地区的北斗区域卫星导航系统已经建设完成,伪距定位精度可达10 m以内,并且初步具备高精度定位能力。GNSS系统具有高精度定位能力,逐渐在各类地形、地貌、地震预警和建筑物变形监测等方面得到广泛应用。随着我国北斗系统的完善与高频(1 Hz)、超高频(20~50 Hz)GNSS定位技术的进一步发展,基于相位观测值的北斗单历元相对定位技术可以快速、准确地获得接收机的位置信息,它可以应用于地震学、火山学等领域,越来越多的国内外学者对其数据处理方法和应用前景产生了浓厚的兴趣[2]。相对定位技术可以大幅度削弱相关误差,获得高精度的定位结果。但是差分技术无法消除多路径误差,在局部监测中,布设的基线较短,在消除其他强相关性的误差后,多路径误差便成为影响监测结果的主要误差源[3, 4, 5, 6]。GNSS系统星座多由轨道具有周期特性的卫星构成,静态观测站的多路径等环境误差将会呈现出周期特性,因此可利用前一天同时段的多路径误差改进后一天定位结果的方法(称为恒星日滤波)[5, 6]。本文探索了北斗系统的多路径误差周期,在获得其周期后,给出了基于北斗系统的恒星日滤波方法。试验结果显示,该方法对北斗多路径效应的消除和卫星地形监测具有重要的意义。
二、北斗单历元基线解算单历元基线解算属于动态相对定位的一种,其观测方程与静态相对定位是相同的[7],因为是单历元解算,考虑到单历元解算若仅采用载波相位观测值会导致法方程秩亏,本文同时加入伪距观测值组建双频伪距及载波相位观测方程。
1. 数学模型进行双差后,可消除接收机和卫星钟差,其观测方程为[7]
式中,下标A、B为测站;上标i、j为观测卫星。其中,A为基准站;i为参考卫星;下标组合表示对测站作差,上标组合表示对卫星作差;P为伪距观测值;dX、dY和dZ分别为基线向量的3个坐标改正数;l、m和n分别为3个坐标方向上的方向余弦;λf是f频率载波所对应的波长;N是载波信号的整周模糊度;I和T分别为电离层延迟改正和对流层延迟改正,当基线长度较短时此两项误差可忽略不计。常数项为 式中,ρ为测站到卫星之间的距离;MP、ML分别为伪距和相位的多路径误差;εP、εL分别为伪距和相位的观测噪声;双差观测值的随机模型为[8] 式中,s表示观测值类型;ns为该类观测值的卫星数。 2. 模糊度固定方法进行快速定位时,虽然观测时间较短,但只要能正确确定整周模糊度,依然能得到高精度的定位结果,因此,基于载波相位观测值的单历元基线解算的关键在于快速确定整周模糊度,文中采用LAMBDA法进行模糊度搜索。
本文采用了较为成熟的on the fly(OTF)技术进行单历元短基线动态定位解算。该解算方法可以概括为两部分:模糊度参数的初始化和固定模糊度后的单历元定位解算[9]。
3. 基线解算算例分析采用和芯星通(UNICORE)公司生产的UB240-CORS北斗/GPS双系统四频接收机(GPS:L1、L2;北斗:B1、B2)对两条小于1 km的短基线进行了数据采集,一条位于北京的超短基线3.066 9 m,数据 时间段为2012年11月8—10日;另一条位于上海同济大学的基线,长度为470.300 9 m,数据时间段为2012年11月8—15日,数据的采样间隔均为1 s。
利用自行编制的北斗数据处理软件,按1 s采样率分别解算了同济大学测站11月8—15日、北京测站11月8—10日的实测数据。同时利用Bernese软件对两个地区的GPS数据进行了解算,将解算得到的观测站坐标作为真值开展后续分析。由于篇幅限制,本文只给出上海站11月8日一天观测数据(采样率1 s,解算历元86 400个)求得的北斗基线相对于标准值的误差序列,如图 1所示。其他时间段观测数据的解算结果如图 2所示。
 |
| 图 1 上海站2012年11月8日北斗基线解算误差时间序列 |
由图 1的误差序列求得北斗基线在北(N)、东(E)、高程(U)各方向上的RMS值分别为0.41 cm、0.30 cm和0.71 cm。
为了评估北斗系统在上海、北京两站的定位表现,对多天解算结果进行了统计分析,如图 2所示。经统计,上海站6天北斗解算结果N、E、U方向误差序列的平均RMS值分别为0.42 cm、0.31 cm、0.80 cm;北京站3天北斗解算结果N、E、U方向误差序列的平均RMS值分别为0.21 cm、0.18 cm、0.55 cm。可以看到,对于这两条短基线数据,北斗单历元基线解算得到了较好的结果。
 |
| 图 2 上海(上)、北京(下)站北斗系统多天基线解算结果坐标三分量RMS统计 |
多路径效应是指北斗信号通过不止一条不同路径到达接收机天线的现象,即对所期望信号经反射或散射后的复制品的接收。多路径误差不仅与观测 环境有关,同时还与卫星的视运动有关。对于静止的观测站,其周边环境长期保持不变,而导航卫星绕地球轨道进行周期性运动,因此观测站接收机的多路径误差具有周期特性,同时与卫星轨道信息高度相关。
1. 基于基线解算结果的北斗多路径误差提取定位解算后的时间序列主要包含载波相位多路径误差和随机噪声,因此该数据可以分析站点相位多路径误差的综合影响。相对多路径信号,随机噪声信号具有高频特性,多路径误差具有低频特性,利用随机噪声和多路径信号的频率特性进行小波滤波提取多路径误差。本文采用db10小波进行7层的小波包分解,剔除高频噪声信号后合成去噪后的新信号。
2. 北斗多路径误差周期特性为了从理论上探讨多路径误差的相关性,计算连续多天多路径误差时间序列的相关性。
算例采用北京、上海两站11月8—10日连续3天的基线数据,先分别进行北斗单历元基线解算,依次获得第1天、第2天、第3天N、E、U方向误差的时间序列,然后对原始解算结果进行小波去噪滤波提取相对纯净的多路径误差(见表 1)。
| station | relevant date | direction | correlation lag/s | max. corr. coefficient |
| Beijing | Day1~2 | N | 244 | 0.513 |
| E | 253 | 0.455 | ||
| U | 247 | 0.469 | ||
| Day2~3 | N | 243 | 0.598 | |
| E | 246 | 0.623 | ||
| U | 242 | 0.590 | ||
| Day1~3 | N | 491 | 0.410 | |
| E | 487 | 0.396 | ||
| U | 488 | 0.322 | ||
| Shanghai | Day1~2 | N | 252 | 0.622 |
| E | 239 | 0.573 | ||
| U | 245 | 0.501 | ||
| Day2~3 | N | 241 | 0.575 | |
| E | 243 | 0.592 | ||
| U | 245 | 0.611 | ||
| Day1~3 | N | 490 | 0.584 | |
| E | 483 | 0.416 | ||
| U | 485 | 0.409 |
从表 1结果可见,相邻两天在相关延迟约为240 s附近出现最大相关,略大于相关延迟的理论值236 s,随着间隔天数的增加,最大相关系数值会逐渐减小[10]。如第1天与第3天的相关值比第1天与第2天或第2天与第3天这类相邻两天的相关值都要低。说明同一地点,随着天数增加,卫星几何条件在发生变化。如上所述,对于静止观测站,北斗多路径效应的周期约为86 160 s,略少于24 h。
3. 多路径误差周期与卫星轨道周期的关系本文介绍了两种方法来确定各个卫星的轨道周期:广播星历法与精密星历法。
(1) 通过广播星历计算轨道重复周期根据广播星历提供的长半轴的平方根和平均角速度摄动参数,由开普勒第三定律得
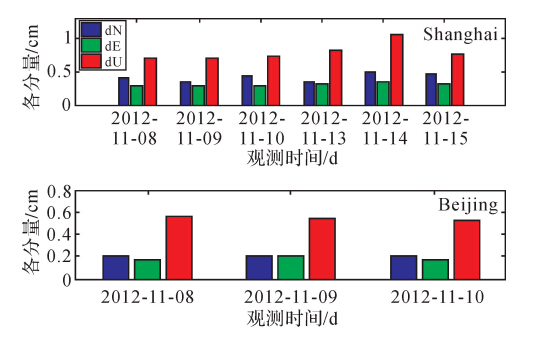
式中,a为卫星轨道椭圆长半轴的平方根;GM为万有引力常数G与地球总质量M的乘积,其值为:GM= 398 600.441 8×109 m3/s2;Δn为平均运动角速度的改正量;T0为卫星运行一周的时间;TR为轨道重复周期。利用2012年6月13日至2012年8月1日这段时间的广播星历求得在这段时间内北斗卫星的轨道重复周期。图 3所示分别为GEO、IGSO和MEO三类卫星的轨道重复周期,其中1—5号、6—10号和11、12号卫星分别为GEO、IGSO和MEO卫星。可以看出,每一类卫星的轨道重复周期都各不相同,对于同一颗卫星来说,每天的运动周期也不完全一致。但是对于每一类卫星,其轨道重复周期都在某一常数附近波动。根据统计,GEO、IGSO和MEO卫星的平均轨道重复周期分别为86 163 s、86 162 s、46 391 s,与以前求得的重复周期基本一致[10]。即卫星每天提前时间分别为237 s、238 s和245 s(北斗MEO卫星与GPS系统的MEO卫星有较大差异,与GPS卫星11 h 58 min的运行周期不同,北斗MEO卫星7 d绕地球运行13圈,7 d累计提前上一周1715 s,平均每天提前245 s,该提前时间与GPS的MEO卫星结果基本一致)。
 |
| 图 3 通过2012年6月13日至8月1日广播星历获得的全部北斗卫星轨道重复周期 |
利用广播星历可以方便、快速地得到卫星的轨道重复周期,然而利用精密星历求得的轨道重复周期更加准确,同时还克服了广播星历计算时并未考虑测站位置信息影响的不足(广播星历计算的重复周期仅仅体现了卫星运行一周的时间)。对于长期静止的观测站而言,为了进一步的数据处理(如恒星日滤波),我们更关心的是卫星相邻2天在测站上空同一位置出现的时间间隔(即地面跟踪重复时间,Duncan Carr Agnew等人在《Finding the repeat times of the GPS constellation》中将它定义为Aspect repeat time,也就是视方位重复时间[10])。
由精密星历计算卫星轨道重复周期的步骤为:
1) 收集观测站的测站坐标(X0,Y0,Z0)及要处理的数据相邻2 d的精密星历。
2) 指定初始参考时间Tr,然后根据精密星历计算Tr时刻各个北斗卫星的空中位置坐标(xi,yi,zi)及测站和卫星构成的各个方向向量ni。
3) 假定经过一个恒星日后,当前时刻T1=Tr+86 164 s,为了得到轨道重复周期的准确值,在T1时刻附近的20 s内进行间隔为0.01 s的搜索,分别将搜索时刻的测站对卫星的方向向量ni与初始参考时间的测站对卫星的方向向量ni进行对比,当矢量ni与ni的夹角最小时,即为该卫星的重复位置,所对应的搜索时刻T′1减去初始参考时间Tr则求得相应卫星的轨道重复周期。
表 2中通过精密星历计算了2012年11月11日 各颗北斗卫星的轨道重复周期。其中,SatID为卫星编号,Tp为精密星历计算结果。有一点需要指出的是,由于北斗MEO卫星7 d绕地球运行13圈(一周运行时间大约12.92 h),无法像GPS卫星一样以天进行对比,一般以一周7 d为周期进行比较,因此在表 2中未进行对比。
| 类型 | SatID | Tp | 86 400-Tp |
| GEO | C01 | 86 163.03 | 236.97 |
| C03 | 86 162.41 | 237.59 | |
| C04 | 86 163.37 | 236.63 | |
| C05 | 86 164.04 | 235.96 | |
| IGSO | C06 | 86 162.78 | 237.22 |
| C07 | 86 161.93 | 238.07 | |
| C08 | 86 160.82 | 239.18 | |
| C09 | 86 163.27 | 236.73 | |
| C10 | 86 162.51 | 237.49 | |
| MEO | C11 | - | - |
| C12 | - | - |
对比以上两种方法的结果,基于广播星历与精密星历计算得到的卫星轨道重复周期与静止观测站北斗多路径误差周期大致相同,验证了多路径误差周期与卫星轨道信息高度相关这一结论。
四、基于多路径误差周期的恒星日滤波GPS系统星座由多颗MEO卫星构成,卫星轨道运行周期为11 h 58 min。接收机位置不变时,第二天提前236 s时刻的卫星与接收机天线相位中心的几何构形在理论上与前一天完全相同,静态观测站的多路径等环境误差将会呈现出周期特性,因此可利用前一天同时段的多路径误差改进后一天定位结果的方法称为恒星日滤波[5, 6, 11]。
北斗系统卫星星座的构成与GPS系统差异较大,其星座由GEO、IGSO、MEO三种不同类型的卫星构成,导致其卫星轨道的重复特性也与GPS相异,因此基于GPS星座特性的恒星日滤波方法不适用于北斗卫星系统。根据上文北斗多路径误差周期计算的结果综合考虑,北斗卫星的平均提前时间约为240 s。
算例根据前文得到的平均重复周期来对基线解算结果进行恒星日滤波。所用数据为上海、北京站连续2 d的短基线数据。北斗系统滤波前后的坐标三分量结果如图 4所示(由于篇幅限制,只绘制了上海站北斗系统的滤波结果图),其他解算结果见表 3、表 4。
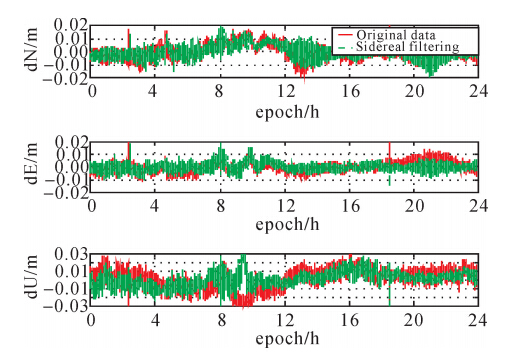 |
| 图 4 2012年11月14日上海站滤波前后的坐标三分量时间序列 |
| RMS N | RMS E | RMS U | |
| 原始数据解算结果/cm | 0.51 | 0.34 | 1.06 |
| 恒星日滤波结果/cm | 0.43 | 0.27 | 0.82 |
| 提升比例/(%) | 15.69 | 20.59 | 22.64 |
| RMS N | RMS E | RMS U | |
| 原始数据解算结果/cm | 0.23 | 0.20 | 0.62 |
| 恒星日滤波结果/cm | 0.19 | 0.18 | 0.55 |
| 提升比例/(%) | 17.39 | 10.00 | 11.29 |
可以看出,恒星日滤波消除了部分周期误差,坐标时间序列的精度有了明显的提高,这说明此方法在北斗数据处理中是具有实际意义的。
五、结 论本文就北斗单历元相对定位解算方法进行了研究,对两条1 km以内的短基线数据进行了测试。根据基线解算结果提取了测站的多路径误差时间序列,并通过最大相关性分析确定了多路径误差的周期,在此基础上提出了适用于北斗系统的恒星日滤波算法。得出以下结论:
1) 对于1 km以内的短基线,北斗单历元相对定位解算可以达到厘米级甚至毫米级的定位结果,北斗系统已经具备高精度定位能力。
2) 对于静止观测站,北斗多路径效应的周期约为86 160 s,与卫星轨道信息高度相关。
3) 北斗恒星日滤波算法消除了部分周期误差,坐标时间序列的精度有了10%~20%的改进,此方法在北斗数据处理中具有实际意义。
| [1] | 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件(测试版)[R]. 北京: [s.n.], 2011. |
| [2] | 殷海涛, 甘卫军, 肖根如. 恒星日滤波的修正以及对高频GPS定位的影响研究[J]. 武汉大学学报:信息科学版, 2011, 36(5): 609-611. |
| [3] | 刘思慧, 樊婧琦, 欧钢, 等. 多径效应的动态特性对码跟踪环路的影响分析[J]. 测绘学报, 2011, 40(S0): 89-94. |
| [4] | 王梦丽, 王飞雪. 三频电离层延迟改正中多路径误差和观测噪声的削弱算法[J]. 测绘学报, 2008, 37(4): 418-422. |
| [5] | CHOI K, BILICH A, LARSON K M, et al. Modified Sidereal Filtering: Implications for High-Rate GPS Positioning[J]. Geophysical Research Letters,2004,31(22). DOI: 10.1029/2004GL021621. |
| [6] | RAGHEB E A, CLARKE P J, EDWARDS S J. GPS Sidereal Filtering: Coordinate and Carrier Phase Level Strategies[J]. Journal of Geodesy,2007,81(5): 325-335. DOI: 10.1007/s00190-006-0113-1. |
| [7] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005. |
| [8] | 魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998. |
| [9] | 胡丛玮, 刘大杰. 单历元确定GPS整周模糊度的分析[J]. 南京航空航天大学学报, 2001, 33(3): 267-271. |
| [10] | MA X Y, SHEN Y Z. Multipath Error Analysis of COMPASS Triple Frequency Observations[J].Positioning,2014,5(1):12-21.DOI:10.42361/pos.2014.51002. |
| [11] | AGNEW D C, LARSON K M. Finding the Repeat Times of the GPS Constellation[J]. GPS Solutions, 2006, 11(3): 71-76.DOI: 10.1007/s10291-006-0038-4. |