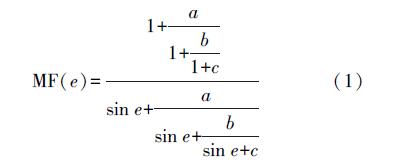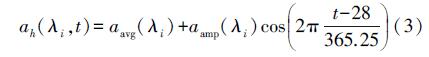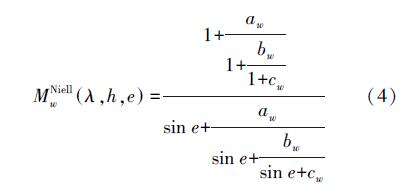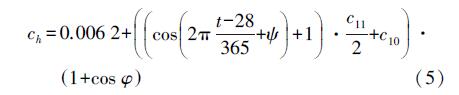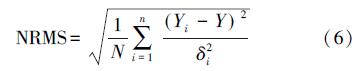一、引 言
GPS信号在穿越地球大气层时,由于电离层和对流层产生时延和弯曲两种效应,从而造成信号传播延迟误差。电离层引起的传播误差可由不同频率的相位组合消除;而对流层由于成分复杂,其误差无法完全消除,目前大多采用建立大气模型的方法来进行延迟改正[1, 2, 3, 4]。而映射函数则是将由对流层模型得到的天顶延迟准确转化为传播路径延迟的关键。因此,选择合适的映射函数对于提高整个模型的准确性和GPS定位的精度有着十分重要的意义。
近年来,国内外学者开展了关于映射函数在GPS数据处理中影响方面的研究。J.Boehm和A.E.Niell等利用1984—2005年的全球VLBI数据对3种映射函数(NMF、VMF1、GMF)进行分析,结果表明使用VMF1可以得到更好的结果,尤其在高程方向上更加明显,其精度在水平方向要比其他函数高出3%,而在高程方向则提高了7%[5]。姜卫平等通过处理某一工程数据,认为GMF模型的精度明显优于NMF模型[6]。徐杰等使用SCIGN、PBO和IGS中的部分测站混合组成观测网进行观测,结果表明NMF和GMF的精度要比CHAO等直接使用地表气象参数的映射函数更好,在亚洲地区更推荐GMF[7]。王君刚等分别使用3种函数模型进行PPP定位,结果发现,VMF1与GMF模型精度相当,两者均优于NMF模型[8]。蒋光伟等利用香港区域CORS站数据进行分析,认为基于VMF1映射函数的基线重复率更好,大地高方向精度有一定的改善,基于GMF映射函数基线重复率优于基于NMF映射函数的结果[9]。
本文采用GAMIT软件,分别使用NMF、GMF及VMF1 3种映射函数对南极地区的GPS数据进行处理,分析上述3种对流层映射函数在南极地区对基线解算的影响。
二、映射函数简介NMF、VMF1、GMF 3种映射函数均属于连分式映射函数,其静力学分量和湿分量映射函数均可表示为下列形式
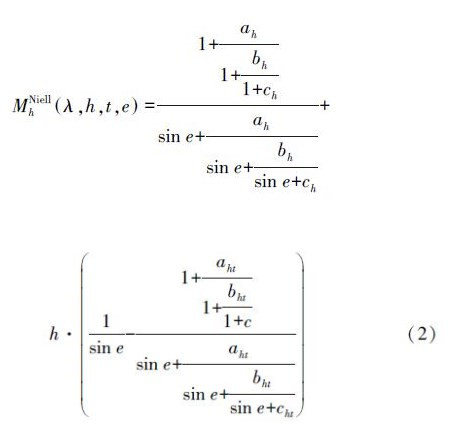
式中,e是高度角;a、b、c是远小于1的常数,且静力学分量和湿分量映射函数各不相同,各个映射函数之间也存在差异。 1. NMF映射函数NMF(Niell mapping function)映射函数是Niell利用43°S至75°N之间的无线电探空站资料,计算建立的全球大气对流层映射函数模型。NMF与之前的映射函数的不同之处在于:其他函数大多取决于地表参数,而NMF则考虑大气层分布随时间的周期性变化,以及南北半球季节非对称性。NMF的静力学映射函数(即干映射函数)仅由测站纬度、高程及年积日决定,其精度在当时优于其他映射函数;而湿映射函数则是仅仅由测站纬度决定[10]。NMF映射函数形式采用式(1),其静力学映射函数表达式为
式中,e为卫星高度角;h为测站海拔高,单位km;aht、bht、cht均为常数(见表 1);ah、bh、ch是与地理纬度λ和观测时间t有关的参数。以ah为例,其计算公式如下 式中,λ为测站纬度;t为年积日;aavg、aamp则是由NMF系数表线性内插而来(见表 1)。其中,当测站高度小于15°时,按照纬度15°时的值进行计算;当测站高度大于75°时,按照75°时的值进行计算。| 名称 | 纬度/(°) | |||||
| 15 | 30 | 45 | 60 | 75 | ||
| 平均项 (average) | ah | 1.276 993 4e-3 | 1.268 323 0e-3 | 1.246 539 7e-3 | 1.219 604 9e-3 | 1.204 599 6e-3 |
| bh | 2.915 369 5e-3 | 2.915 229 9e-3 | 2.928 844 5e-3 | 2.902 256 5e-3 | 2.902 491 2e-3 | |
| ch | 62.610 505e-3 | 62.837 393e-3 | 63.721 774e-3 | 63.824 265e-3 | 64.258 455e-3 | |
| 波动项 (amplitude) | ah | 0.0 | 1.270 962 6e-5 | 2.652 366 2e-5 | 3.400 045 2e-5 | 4.120 219 1e-5 |
| bh | 0.0 | 2.141 497 9e-5 | 3.016 077 9e-5 | 7.256 272 2e-5 | 11.723 375e-5 | |
| ch | 0.0 | 9.012 840 0e-5 | 4.349 703 7e-5 | 84.795 348e-5 | 170.372 06e-5 | |
| 常数项 | aht bht cht | 2.53e-5 5.49e-3 1.14e-3 | ||||
湿映射函数NMFW的计算公式为
式中,aw,bw,cw是与地理纬度λ有关的参数。其计算方式与前文类似,但是由于对流层中湿大气成分所占的比例很小,而其造成的延迟仅占总延迟的10%左右,数值很小,因此,公式中的波动项amplitude不再考虑,仅考虑平均项average即可(见表 2)。其中,当测站高度小于15°时,按照纬度15°时的值进行计算;当测站高度大于75°时,按照75°时的值进行计算。| 相关系数 | 纬度/(°) | |||||
| 15 | 30 | 45 | 60 | 75 | ||
| average | aw bw cw | 5.802 189 7e-4 1.427 526 8e-3 4.347 296 1e-2 | 5.679 484 7e-4 1.513 862 5e-3 4.672 951 0e-2 | 5.811 801 9e-4 1.457 275 2e-3 4.390 893 1e-2 | 5.972 754 2e-4 1.500 742 8e-3 4.462 698 2e-2 | 6.164 169 3e-4 1.759 908 2e-3 5.473 608 3e-2 |
NMF映射函数由于适用于全球且易于实现,以至于后来虽然陆续又有新函数推出但是仍然有人继续使用它。因为NMF并不依赖于地表气象数据,但是和那些需要地表气象输入的映射函数相比精度相当,有时甚至更好,这对在地表气象数据缺失的地区使用对流层映射函数有着尤其重要的意义。不过NMF也存在不足:一是不能反映更短周期的变化(如日变化);二是由于数据的限制,在某些地区会出现较大的系统性偏差。
2. VMF1映射函数VMF1(Vienna mapping function 1)函数由Boehm等在2004年根据欧洲中尺度天气预报中心(ECMWF)提供的数据进行计算而建立,形式上与NMF类似。它利用射线跟踪法得到全球任意2°×2.5°的格网区域,时间分辨率为6 h[11]。系数a即利用上述格网文件内插得到,具体可以从维也纳理工大学网站查询得到;b和c则是利用ECMWF提供的数据资料进行再分析获得,静力学分量bh=0.002 9为常数,而
式中,t为年积日;φ为测站纬度。北半球时,c10=0.001,c11=0.005,ψ=0;南半球时,c10=0.002,c11=0.007,ψ=π。而湿分量系数bw和cw一般分别取0.001 46和0.043 91。VMF1通常被认为是目前全球精度和可靠性较好的映射函数,它的解拥有更好高程结果和坐标重复率,并且不仅可用于静态GPS定位,也可以适用于动态定位和精密大地测量解算中。但是由于该函数是根据实测气象数据得到,因此其有约34 h的时间延迟,实时性较差。另外,由于它基于格网产生并不连续,在某些特殊的时间和地点可能会无法使用。
3. GMF映射函数Boehm等通过将VMF1映射函数的参数在全球格网上进行球谐展开,于2006年提出了新的全球实用的映射函数GMF(global mapping function)。GMF的使用与NMF类似,映射函数中各系数的计算只需用到测站坐标和观测年积日;系数b和c的选取与VMF1相同,a则同样利用格网文件内插获得[12]。在网上可以获得VMF1和GMF映射函数的相关模型及源代码(http://www.hg.tuwien.ac.at/~ecmvmf1/)。
GMF与VMF1都是基于数值天气模型的映射函数。它具有NMF的种种优点而且精度更好,解决了VMF1的时延问题并与其达成很好的契合,即当VMF1在某些地区不能实现时可以用GMF代替求解。因此将GMF作为VMF1的一种后备函数是十分合适的。3种映射函数比较见表 3。
| 映射函数 | 建立时间 | 提出者 | 国家 | 数据来源 | 输入参数 |
| NMF | 1996年 | Neill | 美国 | 无线电探空站 | 测站纬度、高程、年积日 |
| VMF1 | 2004年 | Boehm | 奥地利 | ECMWF | 直接使用全球格网文件 |
| GMF | 2006年 | Boehm | 奥地利 | ECMWF | 测站坐标、年积日 |
选取2011年1月份的南极地区的11个IGS站点(CAS1、DAV1、DUM1、MAW1、MCM4、OHI2、OHI3、PALM、ROTH、SYOG、VESL),以及我国的长城站(GRW1)和中山站(ZHON)两个GPS跟踪站,共计13个站点进行分析,如图 1所示。
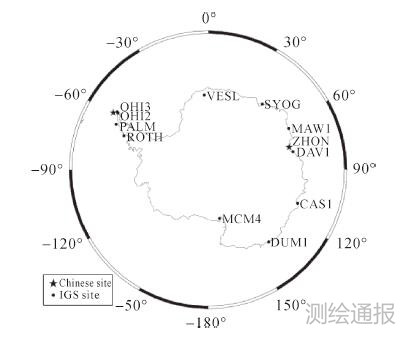 |
| 图 1 南极地区GPS站点图 |
为了比较3种对流层映射函数在南极地区对GPS基线解算的影响,将南极大陆上的11个IGS站设置为固定站,站坐标约束为0.05 m、0.05 m、0.05 m,将中山站和长城站设置为非固定站,站坐标约束为100 m、100 m、100 m。对流层误差采用分段参数估计,每1 h设置一个参数,采用萨斯塔莫宁模型。采用ITRF2000参考框架,空间惯性参考系使用J2000,采用SP3精密星历,电离层模型使用LC-AUTCLN观测量。截止高度角分别设置为5°、10°、15°、20°、25°及30°,利用GAMIT软件分别进行计算。
首先,标准化均方根误差(NRMS)表示单时段解算出的基线值偏离其加权平均值的程度(式(1)),结果如图 2所示。一般情况下NRMS值越小则基线解算的精度越高,其值一般应小于0.3。
从图 2可以看出,上述3种映射函数在相应高度角解算基线得到的NRMS值均小于0.3,解算结果符合要求。采用GMF和VMF1的NRMS要小于NMF,说明采用这两种映射函数处理数据的效果要优于NMF。
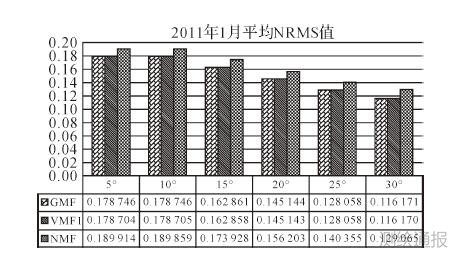 |
| 图 2 2011年1月份平均NRMS值 |
由于基线较多,限于篇幅,选取长城站和中山站各一条基线DAV1-ZHON、OHI3-GRW1,解算结果见表 4和表 5,如图 3和图 4所示。
| 基线名 | 映射函数 | 高度角/(°) | ΔN/mm | ΔE/mm | ΔU/mm |
| DAV1_ZHON | NMF | 5 | 2.6 | 2.0 | 8.0 |
| 10 | 2.6 | 2.1 | 8.1 | ||
| 15 | 4.0 | 2.7 | 10.4 | ||
| 20 | 6.0 | 3.6 | 17.1 | ||
| 25 | 7.8 | 5.2 | 34.0 | ||
| 30 | 8.4 | 6.8 | 60.3 | ||
| VMF1 | 5 | 2.2 | 1.6 | 7.1 | |
| 10 | 2.2 | 1.6 | 7.1 | ||
| 15 | 2.9 | 2.1 | 9.6 | ||
| 20 | 4.0 | 2.7 | 14.4 | ||
| 25 | 5.8 | 3.6 | 23.3 | ||
| 30 | 6.0 | 4.7 | 40.7 | ||
| GMF | 5 | 2.4 | 1.8 | 7.5 | |
| 10 | 2.4 | 1.8 | 7.5 | ||
| 15 | 3.4 | 2.4 | 9.9 | ||
| 20 | 4.9 | 2.9 | 14.9 | ||
| 25 | 6.4 | 3.9 | 23.6 | ||
| 30 | 6.9 | 5.0 | 41.9 | ||
| 基线名 | 映射函数 | 高度角/(°) | ΔN/mm | ΔE/mm | ΔU/mm |
| DAV1_ZHON | NMF | 5 | 2.9 | 2.5 | 8.8 |
| 10 | 2.9 | 2.5 | 8.8 | ||
| 15 | 4.5 | 2.9 | 12.2 | ||
| 20 | 6.5 | 4.6 | 22.8 | ||
| 25 | 9.7 | 7.0 | 43.0 | ||
| 30 | 10.7 | 7.8 | 70.5 | ||
| VMF1 | 5 | 2.3 | 2.0 | 7.1 | |
| 10 | 2.3 | 2.0 | 7.1 | ||
| 15 | 2.9 | 2.2 | 9.3 | ||
| 20 | 3.9 | 2.7 | 13.3 | ||
| 25 | 5.3 | 3.5 | 20.7 | ||
| 30 | 6.6 | 4.2 | 31.5 | ||
| GMF | 5 | 2.5 | 2.2 | 7.4 | |
| 10 | 2.5 | 2.2 | 7.4 | ||
| 15 | 3.3 | 2.4 | 9.8 | ||
| 20 | 4.4 | 2.8 | 13.8 | ||
| 25 | 6.0 | 4.0 | 21.7 | ||
| 30 | 7.3 | 4.5 | 32.6 | ||
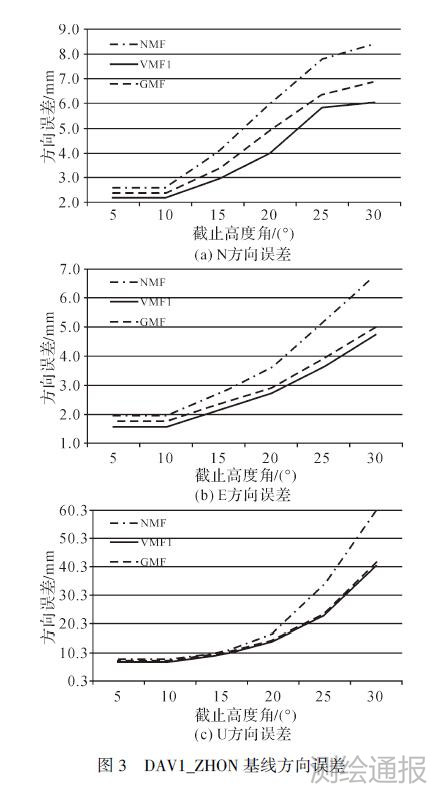 |
| 图 3 DAV1_ZHON基线方向误差 |
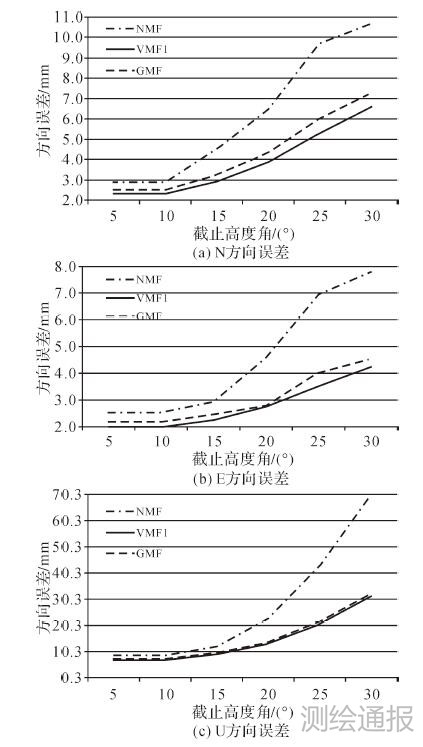 |
| 图 4 OHI3-GRW1基线方向误差 |
从表 4、表 5及图 3、图 4中可以看出,3种映射函数在N方向的误差优于11 mm,在E方向的误差优于8 mm,而在U方向,误差达到70 mm,说明3种映射函数在水平方向误差较小,而在垂直方向误差较大。高度角为5°和10°时,解算结果几乎没有差别,随着高度角的增大,3种映射函数在N、E、U 3个方向的误差也随着增大。高度角为5°时,由于高度角较低,所受对流层延迟的影响较大,因此在南极地区进行高精度GPS数据处理时,综合考虑对流层延迟和卫星几何分布等方面的影响,建议采用10°的高度角。在各个高度角下,NMF映射函数在N、E、U 3个方向误差均要明显大于GMF和VMF1,说明主要基于北半球测站数据建立的NMF映射函数在南极地区存在较大的误差,VMF1映射函数在N、E、U 3个方向的结果要略好于GMF,不过由于GMF是由VMF1进行球谐展开得到,具有很好的连续性,而这正好可以弥补VMF1不连续的缺点,因此在南极地区推荐优先使用VMF1,GMF作为备用函数。
四、结束语本文利用南极地区我国的长城站、中山站及11个IGS站1个月的数据,截止高度角分别设为5°、10°、15°、20°、25°及30°,比较了NMF、VMF1和GMF 3种映射函数在南极地区对GPS基线解算的影响,结果表明:
1) NMF、VMF1和GMF 3种映射函数在水平方向误差较小,约为11 mm,而在垂直方向误差较大,达70 mm。
2) 随着高度角的增大,3种映射函数在N、E、U 3个方向的误差也随着增大,综合考虑对流层延迟和卫星几何分布等方面的影响,建议采用10°的高度角。
3) 在各个高度角下,NMF映射函数在N、E、U 3个方向误差均要明显大于GMF和VMF1,VMF1的效果要略好于GMF,因此在南极地区推荐优先使用VMF1映射函数。
| [1] | 李昭, 邱卫宁, 邱蕾,等. 几种对流层延迟改正模型的分析与比较[J]. 测绘通报, 2009(7):16-18. |
| [2] | 葛茂荣, 刘经南. GPS定位中对流层折射估计研究[J]. 测绘学报, 1996,23(4):285-291. |
| [3] | 姚宜斌, 胡羽丰, 余琛. 一种改进的全球对流层天顶延迟模型[J]. 测绘学报, 2015, 44(3):242-249. |
| [4] | 李征航,张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉:武汉大学出版社, 2009. |
| [5] | BÖHM J, NIELL A E, SCHUH H, et al. Mapping Functions for Atmospheric Delay Modelling in GNSS Analysis[R]. Wien:[s.n.],2006. |
| [6] | 姜卫平, 李昭, 邱蕾. 一种最新的经验投影函数GMF分析[J]. 大地测量与地球动力学, 2009, 29(5):85-88. |
| [7] | 徐杰, 孟黎, 任超, 等. 对流层延迟改正中投影函数的研究[J]. 大地测量与地球动力学, 2008, 28(5):120-124. |
| [8] | 王君刚, 陈俊平, 王解先. GNSS对流层延迟映射模型分析[J]. 天文学进展, 2014, 32(3):383-394. |
| [9] | 蒋光伟, 田晓静, 王斌,等. 高精度GNSS服务中对流层映射函数的影响性分析[J]. 测绘工程, 2013, 22(5):13-15. DOI:10.3969/j.issn.1006-7949.2013.05.004. |
| [10] | NIELL A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 1996, 101(B2):3227-3246. |
| [11] | KOUBA J. Implementation and Testing of the Gridded Vienna Mapping Function 1(VMF1)[J]. Journal of Geodesy, 2008, 82(4-5):193-205. |
| [12] | BÖHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7):1-4. |