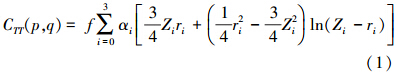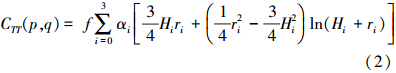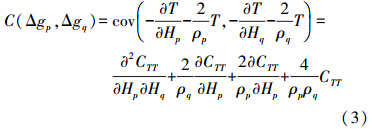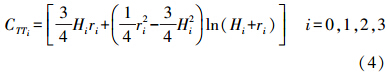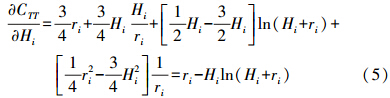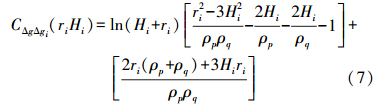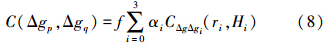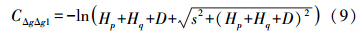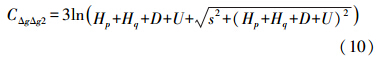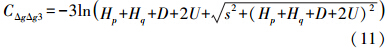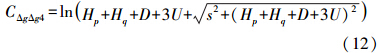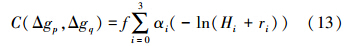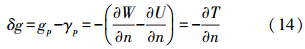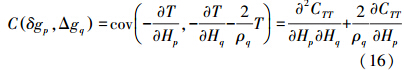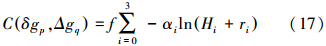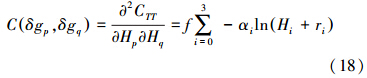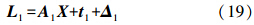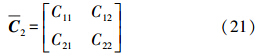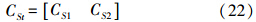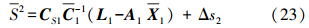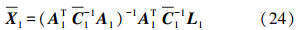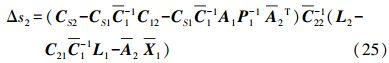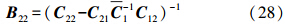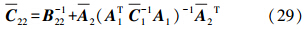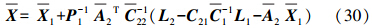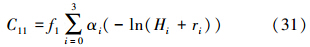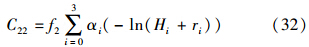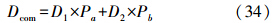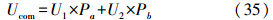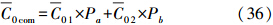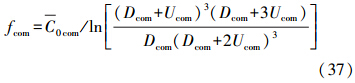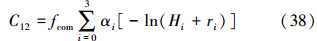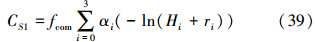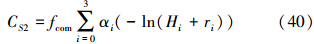一、引 言
目前,利用航空重力测量技术获取局部区域的高分辨率重力场信息成为一个非常有效的手段。在航空测量数据处理中,传统的技术流程是先将观测得到的航空扰动重力数据进行滤波、格网化,然后转化为重力异常数据,最后向下延拓至对应的地面区域获得最终的地面重力异常数据[1]。上述数据处理过程往往会使测量数据受到不当的处理(如采用不准确的模型)而影响最终数据的质量(如存在一定的系统误差)。如果能找到一种直接利用测线扰动重力数据进行处理的方法则可以在减少处理流程的同时提高产品数据的精度。在航空重力测量实施的区域,地面上或多或少会有已知的重力异常测量点,这些测量点的重力数据较之航空测量精度更高,因此,如何将地面已知重力数据有效利用起来构建航空和地面一体化的处理方法成为国内外学者关注的重点。最小二乘配置法具有联合多种数据类型的处理优势[2, 3, 4, 5],然而在运用最小二乘配置法进行处理时,多数学者都是在固定的协方差模型及模型参数下进行解算,即所有观测数据都采用同一个先验信息,而后按照该先验信息完成数据的推估和滤波[6, 7, 8]。针对上述问题,本文将在最小二乘配置法基础上,构建一种能够对航空和地面重力数据进行一体化处理的方法,该方法应顾及不同高度和不同数据类型,且兼具格网化和向下延拓等功能。
二、局部重力异常的协方差模型构建能够反映局部重力场空间变化的重力异常协方差模型是进行一体化处理的基础工作。根据文献[3]的研究成果,采用扰动位的三维协方差经验模型如下
式中,f表示比例系数;α0=1,α1=-3,α2=3,α3=-1;ln表示自然对数函数;Zi=Zp+Zq+Di;i=0,1,2,3;D表示高频衰减因子;U表示低频衰减因子;Di=D+iU,D、U含义同上;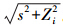 。其中,s=
。其中,s=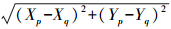 ,s表示空间两点p、q间的平面距离,X、Y、Z表示观测点的三维坐标。
,s表示空间两点p、q间的平面距离,X、Y、Z表示观测点的三维坐标。考虑到局部区域的应用环境,将式(1)用大地坐标替换得到如下形式的局部扰动位协方差模型
式中,f、α具体含义同上式;Hi=Hp+Hq+Di,Hp、Hq代表p、q两点的大地高。
根据扰动场元间的线性关系,按照协方差传播定律可得p、q两点重力异常间协方差为
式中,CTT表示扰动位协方差模型;ρp、ρq分别是p、q两点的地心向径。
考虑到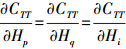 ,以及扰动位协方差模型的4部分具有相同的形式,即
,以及扰动位协方差模型的4部分具有相同的形式,即
对扰动位协方差模型的通用形式CTT求导得 二阶导数为
将式(5)、式(6)代入式(3)得到局部重力异常协方差的一般形式为
其完整形式为
式(8)虽然严密,但过于复杂,不利于实际应用,若能在保证效果的前提下进行简化,则更具有实用价值。由于航空重力测量高度有限,同时考虑到局部重力场的测量区域有限,
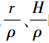 的最大量级一般在0.1左右,再加上模型的4个部分会有一定的抵消,因此这个量级对结果应该没有大的影响。实际计算也证明对最终结果的影响在1/100量级,因此在模型中可以忽略有关这两部分的影响,通过进一步简化后得到局部重力异常协方差模型的4部分分别为
的最大量级一般在0.1左右,再加上模型的4个部分会有一定的抵消,因此这个量级对结果应该没有大的影响。实际计算也证明对最终结果的影响在1/100量级,因此在模型中可以忽略有关这两部分的影响,通过进一步简化后得到局部重力异常协方差模型的4部分分别为模型的完整形式为
式(9)—式(13)即为简化后的局部重力异常的协方差实用模型。 三、局部扰动重力和重力异常的互协方差模型
扰动重力与扰动位间的关系为
考虑到椭球面上大地高方向H与n方向相同,因此
按照协方差传播定律可得空间扰动重力观测点p和地面重力异常待求点q的互协方差为
将局部扰动位协方差模型CTT代入上式并忽略小项得到互协方差模型为
式(17)即扰动重力与重力异常互协方差模型的完整形式。
同理,局部扰动重力的自协方差模型按照上述原理推导如下
将式(18)、式(17)与式(13)对比发现,扰动重力与重力异常互协方差模型与重力异常协方差模型、扰动重力协方差模型形式上完全一致,这样在航空扰动重力数据和地面重力异常数据处理时只采用同一个协方差模型即可。
四、一体化处理方法假设航空扰动重力数据观测值为L1,地面重力异常数据观测值为L2,对应的观测信号为t1、t2,对应的观测噪声分别为Δ1、Δ2,航空重力数据对应的系统性参数为X,此时得到两组观测方程分别为
式中,A1为系数阵;观测值的协方差阵为
式中,C11、C22表示两组数据的自协方差;C21、C12表示两组数据的互协方差。
未测信号S(地面未测点的重力异常)与已测信号t的互协方差为
按照经典理论可推导获得未测信号的推估公式[9, 10, 11]如下
式中,C-11=C-111;X1表示由第一组观测值求出的系统性参数
式中
系统参数的估值为 根据大量的试验分析和理论推导,采用以下计算步骤。对于两类数据的自协方差,分别采用各自的参数计算即Δg1的自协方差C11为
Δg2的自协方差为
对于两类数据的互协方差的计算,首先加入两个调整因子Pa、Pb对模型参数进行调整,为了保证加入调整因子后的参数符合实际情况,Pa、Pb应满足如下关系
利用Pa、Pb对模型参数进行调整得到
Dcom、Ucom、C0com分别表示调整后的高、低频因子和区域方差值,利用这些调整后的参数可以得到协方差模型的比例系数
利用Dcom、Ucom、C0com、fcom计算两种数据的互协方差(C12与C21等价)
由于未测信号的先验信息未知,因此未测信号与已测信号的互协方差也按照调整后的模型参数计算
在实际应用中,Pa、Pb需要进行迭代计算,迭代循环的截止条件则以每次计算获得的单位权中误差作为评判依据,当前后两次获得的单位权中误差之差小于某个限值时,循环结束,如图 1所示。
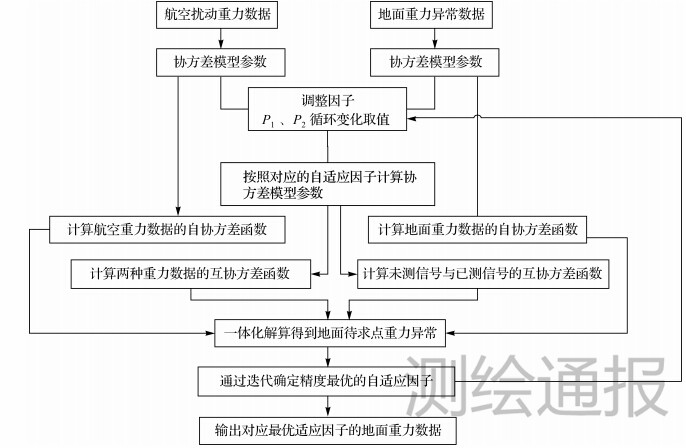 |
| 图 1 航空和地面重力数据一体化处理流程 |
试验区位于我国陆地某区域,该区域航空重力测量与陆地重力数据分布如图 2所示,整个区域有分辨率为5′×5′的航空扰动重力数据(飞行平均高度3600 m,测线数据采样频率为1 Hz)和2.5′分辨率的地面重力异常数据,地形数据采用SRTM 90 m分辨率的地形模型。为了检验一体化处理算法,本文假设参与地面重力异常数据ΔgT布设形式为均匀分布,如图 3所示,其中“★”代表参与一体化处理的地面重力数据,其余空格区域代表需要求解的重力数据,同时也用来对一体化处理结果进行检核。
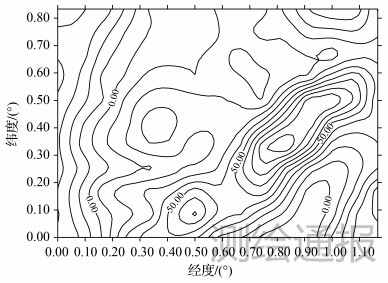 |
| 图 2 航空重力测量与陆地重力数据分布 |
 |
| 图 3 地面重力数据呈均匀分布 |
首先利用航空扰动重力数据进行格网化,然后利用直接代表法向下延拓[12]获得地面待求点数据。其次利用地面重力数据按照经典的最小二乘配置法推估该区域待求点重力数据,两种方法分别与已知的地面重力数据进行比较,见表 1。
最后按照本文提出的一体化处理方法,利用航空扰动重力的测线数据求解地面待求点重力数据,统计结果见表 2,最终处理后的地面重力异常数据如图 4所示。
 |
| 图 4 航空和地面重力数据一体化处理后的三维重力图 |
通过表 1、表 2对比可以看出,一体化处理方法比单独使用航空和地面重力数据进行推估的效果都要好,这也说明了一体化处理方法对于联合处理航空和地面重力数据是非常适用的。
本文深入研究了航空扰动重力数据和地面重力异常数据的联合处理问题,构建了一种一体化处理方法,主要结论和创新点如下:
1) 在三维扰动位协方差模型基础上,推导获得局部重力异常协方差模型、局部扰动重力协方差模型,以及扰动重力和重力异常的互协方差模型。这3个模型在忽略小项后是一致的,即航空扰动重力数据与地面重力异常数据的联合处理采用一个模型即可,大大简化了处理流程,提高了计算效率。
2) 以最小二乘配置法为基础,构建了航空扰动重力数据与地面重力异常数据一体化处理的具体方法和实施步骤,利用该方法可推估地面任意待求点的重力数据,并可有效估计航空重力数据中的系统偏差。
3) 在某试验区开展了一体化处理试验,结果表明,采用一体化处理获得的重力异常数据比单独使用5′分辨率航空重力数据推估获得的数据精度提高2.4 mGal,比单独使用2.5′分辨率地面重力数据推估获得的数据精度提高1.2 mGal,且一体化处理过程自动完成了航空扰动重力数据的向下延拓,同时也大大削弱了航空数据中存在的系统偏差。
本文所构建的航空扰动重力数据和地面重力异常数据的一体化处理方法将为未来我国大规模的航空重力测量及磁力测量数据处理提供很好的参考和借鉴。
| [1] | 孙中苗。航空重力测量理论、方法及应用研究[D].郑州:中国人民解放军信息工程大学,2004. |
| [2] | OLESEN A V, ANDERSEN O B, TSCHERNING C C. Merging of Airborne Gravity and Gravity Derived from Satellite Altimetry: Test Cases Along the Coast of Greenland[J]. Studia Geophysica et Geodaetica, 2002, 46(3): 387-394. |
| [3] | STRYKOWSKI G, FORSBERG R. Operational Merging of Satellite, Airborne and Surface Gravity Data by Draping Techniques[C]//Geodesy on the Move: Gravity, Geoid, Geodynamics and Antarctica. Berlin: Springer Verlag, 1997: 243-248. |
| [4] | BAYOUD F A. Some Investigations on Local Geoid Determination from Airborne Gravity Data[D]. Calgary, Canada:University of Calgary,2001:33-35. |
| [5] | HWANG C, GUO J Y, DENG X L, et al. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry:Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204-216. |
| [6] | 郝燕玲,成怡,刘繁明,等。融合多类型海洋重力数据算法仿真研究[J]. 系统仿真学报,2007, 19(21): 4897-4899. |
| [7] | KERN M, SCHWARZ K K P P, SNEEUW N. A Study on the Combination of Satellite, Airborne, and Terrestrial Gravity Data[J]. Journal of Geodesy, 2003, 77(3-4): 217-225. |
| [8] | 杨元喜,曾安敏。大地测量数据融合模式及其分析[J]. 武汉大学学报:信息科学版,2008, 33(8): 771-774. |
| [9] | 杨元喜,张菊清,张亮。基于方差分量估计的拟合推估及其在GIS误差纠正的应用[J]. 测绘学报,2008, 37(2): 152-155. |
| [10] | 陆仲连。地球重力场理论与方法[M]. 北京:解放军出版社,1996: 316-320. |
| [11] | 邹贤才。最小二乘配置在物理大地测量中的应用[D]. 武汉:武汉大学,2003. |
| [12] | 王兴涛,夏哲仁,石磐,等。航空重力测量数据向下延拓方法比较[J].地球物理学报,2004,47(6):1017-1022. |