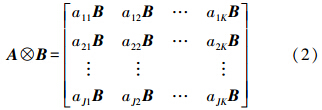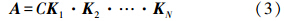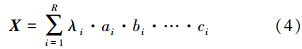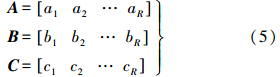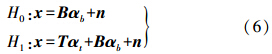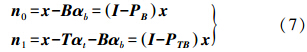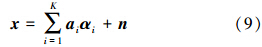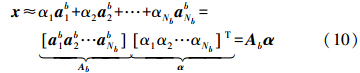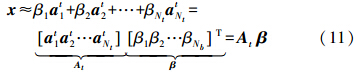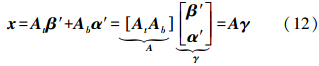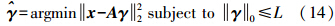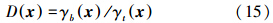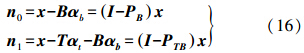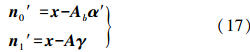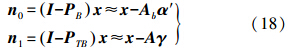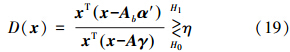一、引 言
高分辨率对地遥感观测系统的搭载平台主要有星载平台和机载平台两种,星载平台观测范围广,收集速度快,但其观测轨道是固定的,观测分辨率不能随任务而修正。机载平台作为一种十分灵活的遥感观测方式,通过控制飞行高度和更换搭载观测仪器,可使空间/光谱分辨率达到更高的水平,这对于局部区域的高精度信息探测十分有利。因此,各国都在大力发展机载高分辨率遥感观测系统。该类研究国外相对较早,技术也十分成熟,各种产品都处于主导地位。近些年国内也在大力发展高分遥感,国家适时地提出了“高分辨率对地观测系统重大专项”,简称“高分专项”,而航空观测系统便是“高分专项”的重要组成部分。它以大气层航空飞行器为载体,由飞行平台、对地观测设备和地面数据处理系统3部分组成,可获取可见光和微波等各类高分辨率数据,经数据处理形成对地观测信息,服务于基础测绘、灾害监测、资源和环境调查、气象水文观测等众多领域。
在硬件平台蓬勃发展的同时,基于任务驱动的高分遥感也在不断前进,目标检测作为遥感的主要应用之一,在高分辨率对地观测发展的大环境下,面临着新的任务和挑战。在马航搜救行动中,即可看出高分遥感发展的重要性,但目前面临高分目标的检测问题时还存在能力的不足。在高分辨率对地观测背景下,目标检测的最小尺度会不断提升,尺度较大目标的检测完整性和检测正确性不断提高;但与此同时,高分观测带来的空间信息冗余和光谱波段间冗余也随之增大,如何在冗余的空-谱信号中有效地挖掘目标信息是高分背景下目标检测应首要解决的问题。
当前的目标检测手段主要有3种:异常检测[1, 2, 3]、已知样本下的光谱匹配检测和一分类方式的检测[4]。而作为主流的光谱匹配检测模型主要有欧氏距离模型,概率统计模型与子空间模型[5, 6],这方面的代表性研究机构有美国海军空战中心武器分部和美国马里兰陆军研究实验室:H. Kwon等在异常检测领域提出了最优全对角带宽系数的Gaussian RBF kernel检测技术[7]。而Trac D. Tran等在光谱匹配检测,尤其是稀疏匹配检测领域作出了很多前瞻性的研究,包括提出了一种基于稀疏表示的高光谱图像自动目标检测算法,这种算法的思想是高光谱图像的像素位于一个低维子空间,从而可以用训练样本的稀疏线性组合对像素进行表示,对测试样本的稀疏表示可以通过求解零范数最小值问题获得,一旦得到了稀疏向量,测试样本的类别可以通过重建的稀疏向量特征进行判断[8];在此基础上,考虑空间邻域信息的影响,又提出了联合稀疏模型用于高光谱图像目标检测[9];针对高光谱图像的非线性特性,在原来的稀疏目标检测基础上引入核方法,提出了核稀疏表示的高光谱图像目标检测算法[10]。
当前目标检测主要利用光谱匹配特性,通过光谱匹配程度判断单点光谱的属性,并未充分考虑在高分条件下空间约束增强的特性,即局部相关性增大的特性,空谱联合检测方法可以提高光谱和空间的利用能力,但一般的空谱联合方法仅仅从光谱或空间的简单组合操作进行分析,而不能从三维数据整体进行信息挖掘。
张量分析作为高维数据整体分析的有效工具[11, 12],可有效挖掘高维数据整体信息,同时,基于Kruskal张量分解的信号,在保留信号原有特征的同时舍去信号的冗余,降低光谱噪声影响。信号在张量分解后各个方向上的分量又保留着各自独立的信号属性:在x、y方向的分量可视为光谱维方向的整体变化趋势,而光谱维方向的分量恰恰是信号属性的缩影,即光谱维方向上投影可视为目标属性分量,因此,Kruskal张量分解对于目标的检测和属性分析有其他方法无法比拟的优势。
鉴于张量分解在三维空谱联合分析中的优势,本文提出了一种基于Kruskal秩一张量分解的稀疏匹配子空间目标检测方法。算法首先利用基于CP优化的Kruskal分解[13],获取一阶秩一张量[14]作为信号的去冗余近似,并将三维投影分量重组为新的光谱维取代原始中心点光谱,以此挖掘出空谱三维联合信息;然后通过将匹配子空间和稀疏检测方法联合得到稀疏匹配子空间检测方法,该方法可有效解决匹配子空间检测时正交向量的难于求取问题,同时又将子空间检测模型的理论优势与稀疏检测优势相结合,本文将该结合方法用于张量分解后的目标检测;最后本文在两组高光谱目标数据中进行验证,并将该方法与稀疏方法、拉普拉斯空谱约束检测方法[15]和协同稀疏空谱联合方法[9]进行对比。
二、高光谱图像的张量表示张量又称多阶阵列,是数据从一维(向量)、二维(矩阵)向高维数的扩展,而高光谱图像数据立方体就是一个典型的三阶张量。设N阶张量为A∈RI1×I2×…×IN,张量A中所含有的点的个数为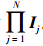 。图 1所示为一个属于RI×J×K的三阶张量示意图。
。图 1所示为一个属于RI×J×K的三阶张量示意图。
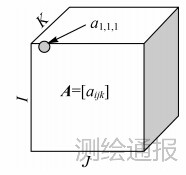 |
| 图 1 典型的三阶张量 |
对于外积运算,熟知的向量外积运算为
式中,U=[u1 u2 … um];V=[v1 v2 … vn]。
而张量的Kronecker product 运算可以定义为
式中,A∈RJ×K;B∈RM×N。
经过外积运算后,新的张量维数是原始两个张量维数之和(M+N),即A∈RI1×I2×…×IN,B∈RJ1×J2×…×JM,A⊗B∈RI1×I2×…×IN×J1×J2×…×JM。假如有N个一维向量Ki(i=1,2,…,N),向量的元素个数分别为I1,I2,…,IN,则可以把这N个一维向量组成一个N阶的张量K1·K2·…·KN=A。凡是能用这种方式表述的张量称之为秩一张量。反之,将一个秩一张量A分解为N个一维向量的过程称之为张量A的秩一分解。但通常需要添加一个比例系数,即张量的秩一分解为
张量的秩一分解是最主要的张量分解形式[16]的一种,又叫Kruskal张量分解。如果一个张量可以由R个秩为一的张量经过线性叠加而成,则可以认为这个张量的秩为R,假设张量X的秩为R,则Kruskal分解可以描述如下
式中,A、B、C分别为3个方向的秩一分量,表示为
故此三阶张量的Kruskal张量分解过程如图 2所示。
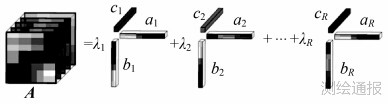 |
| 图 2 三阶高光谱张量Kruskal分解示意图 |
对于高光谱目标检测,目标光谱可以视为背景光谱与典型目标光谱的线性组合,即目标和背景像素向量可由典型光谱子空间和背景光谱子空间的线性组合来表示。这种利用子空间线性组合表述光谱的方式被称为线性子空间模型。而目标检测问题可以看作是两种假设H0和H1的竞争问题
式中,H0假设代表无目标情况;H1代表有目标情况,T和B是两个矩阵,它们的列向量分别张成了目标和背景子空间;αt和αb是未知系数向量,代表着相应于目标和背景子空间T与B的丰度;n为噪声项。如果x是目标像素,它趋向于由假设H1表示;否则它趋向于由假设H0表示。可以通过检查输入信号是否包含目标子空间信号来识别它是否为目标像素。由式(6)可以得到 式中,输入向量向子空间进行投影,实际上是提供了线性子空间模型的最小均方解;PB是相应于背景子空间的投影矩阵;PTB是相应于目标和背景子空间的投影矩阵。线性子空间检测模型的GLRT形式为
即是匹配子空间检测模型。
通过选择合理的阈值ηMSD,当DMSD(x)>ηMSD,则x被标记为目标;反之标记为背景。
2. 稀疏目标检测模型稀疏表示目标检测方法是假定每一个像素都可以由一个过完备字典中少量的原子的线性组合来表示。这种思想与线性子空间检测模型的思想本质上是相同的。
给定一个高光谱像素x,设它为一个P维向量,P为光谱波段数。令A=[a1,a2,a3,...,aK]∈RP×K(P≤K)为一个过完备字典,则对于一个高光谱像素x,它可以表示为
式中,{αi}是分解系数;n是噪声。
对于高光谱图像目标检测问题,假定像素x是目标或背景像素中的一种。当像素x是背景像素时,它可以近似地表示为
式中,Ab是背景字典;α是一个只含有少量非零元素的向量,非零元素的位置也就相当于字典Ab中相应的原子;Nb是背景字典中原子的个数。
类似地,当像素x是一个目标像素时,它也可以近似地表示为
式中,At是目标字典;β是一个只含有少量非零元素的向量,非零元素的位置也就相当于字典At中相应的原子;Nt是背景字典中原子的个数。
在基于稀疏的检测模型中,一个未知的测试像素x可以表示成由目标和背景联合子空间中原子的线性组合。因此,组合目标字典At与背景字典Ab,得到一个新的过完备字典A。然后,测试像素x可以表示为
式中,β′和α′是相应于两个字典的系数。然而,在进行表示时,通常认为线性表示所需要的组合元素是较少的,即系数向量γ是稀疏的,这个问题可以描述如下
但零范数的优化求解是一个NP-hard问题,为方便求解,通常将其转化为1范数进行优化求解,即
式中,L是稀疏度,并且有L≥1。
上述优化问题可利用凸优化方法或贪婪追踪算法来解决,如orthogonal matching pursuit (OMP)算法[17]或subspace pursuit (SP)方法[18]。
获取稀疏系数向量后,就可以通过比较残差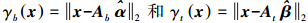 的大小来判定测试像素x是目标还是背景。因此,检测器的输出计算公式为
的大小来判定测试像素x是目标还是背景。因此,检测器的输出计算公式为
如果D(x)>η,那么x可以被认为是目标像素;否则x是背景像素。η是给定的阈值。
3. 稀疏匹配子空间检测模型通过比较匹配子空间检测(MSD)模型与稀疏表示的目标检测方法可知,两者在本质上极为相似,都可视为线性子空间模型。在该模型下,测试像素都是假定可以由目标和背景类张成的子空间来表示。区别在于基于稀疏表示的目标检测方法是用过完备字典来代替子空间模型中的子空间。
匹配子空间模型有较好的目标检测模型解释能力,但要求子空间内元素必须正交,这对于子空间的构建和模型的泛化十分不利,但如果借助于稀疏表示的字典空间代替匹配子空间,则可以利用现有的稀疏字典学习和稀疏求解框架进行求解,使得该子空间匹配模型得到推广,因此,可以结合匹配子空间检测方法与稀疏表示方法,提出一种稀疏匹配子空间检测(Sparse MSD,SMSD)模型,该模型结合了匹配子空间检测模型和稀疏表示的目标检测方法的优势,有着更好的检测性能。
从线性子空间检测模型可以得到
由稀疏表示理论,可以得到
从式(16)、式(17)可知,其噪声项在物理意义和形式上都是类似的,将两者结合,可以得到
将式(18)代入式(8)中,可以得到新的检测方法,即SMSD方法
从式(19)可以看出,对于一个测试像素x来说,想要通过SMSD方法来判断其是目标还是背景,在已有目标和背景字典的情况下,需要先通过OMP等方法来求解出相应的稀疏系数α′和γ,然后,类似于匹配子空间模型,如果D(x)>η,那么X可以被认为是目标像素;否则,X是背景像素。η是给定的阈值。
4. 稀疏张量目标检测算法流程本文的核心思想是利用Kruskal分解挖掘空间和光谱的三维一体协同信息,并在挖掘后信息的基础上,通过将匹配检测和稀疏检测方法相结合的稀疏匹配检测方式,提高挖掘信息后的目标检测精度和准确性。
下面给出稀疏张量目标检测算法(Kruskal SMSD)的详细流程,输入高光谱图像、邻域尺度k、稀疏度L,输出检测结果图D。
1) 对于原始高光谱图像张量X中每一个像素,取周围k×k邻域,构建三阶张量,通过CP优化方法进行Kruskal秩一分解,获取一个最近似秩一张量,将该张量3个投影向量重组为一维向量并取代原始中心点光谱。
2) 设定字典中背景与目标原子数目,通过已有的目标真值图选取部分背景与目标光谱构建原始字典,然后利用KSVD算法进行字典训练,获取优化字典Ab和At。
3) 将得到系数α′和γ代入到目标函数中,即式(19),得到检测结果D。
四、试验与结果 1. 数据来源介绍为验证算法的检测性能,共收集两组数据进行测试,分别是2013年和2014年IEEE国际遥感数据融合竞赛的比赛数据[19, 20],鉴于数据量过大,这里仅截取其中的部分进行测试试验。2013年融合竞赛所采用的数据为空间分辨率2.5 m的可见光高光谱数据(外加激光雷达数据),而2014年数据融合比赛采用空间分辨率为1 m的长波红外高光谱数据(以及相应的可见光全色图)。而常见的遥感高光谱图像空间分辨率都在5~10 m级别,因此,这种米级或接近米级的高分辨率高光谱图像非常适合于测试算法对高分辨率高光谱图像的适用性。图 3(a)为2014年红外高光谱图像测试数据相应区域的RGB图;图 3(b)为其相应的车辆的真值图;图 3(c)为2013年可见光高光谱图像测试数据区域的伪彩色图;图 3(d)为图 3(c)图相应车辆目标的真值图。
 |
| 图 3 两组真实航空高光谱成像测试数据 |
为验证算法的有效性和优越性,本文通过结合常见的检测方法(一般稀疏检测)或联合处理方法(拉普拉斯空谱联合和联合稀疏方法)与本文提出的思想进行了对比试验,对比方法包括:一般稀疏检测(Sparse)、稀疏匹配检测(SMSD)、拉普拉斯空谱联合稀疏检测(Laplacian Sparse)、拉普拉斯空谱联合稀疏匹配子空间检测(Laplacian SMSD)、联合稀疏检测模型(Joint Sparse)、张量低秩分解一般稀疏检测(Kruskal Sparse)和基于张量低秩分解的稀疏匹配子空间检测(Kruskal SMSD)。
在对比试验中,分别给出了各种算法的AUC值、ROC曲线、检测效果图和稀疏度对算法AUC指标的影响曲线。
3. 试验结果表 1是各种算法在不同稀疏度下对红外高光谱图像的目标检测性能AUC指标。取AUC的最大值进行对比。从表 1可以看出,Kruskal分解的稀疏和稀疏匹配子空间检测方法要比原始光谱的稀疏和稀疏匹配子空间方法检测效果好,稀疏匹配子空间检测方法对于原始稀疏检测有着明显的提高,而且,基于Kruskal分解的稀疏匹配子空间检测方法要优于其他所有方法和组合检测方法。因此,在该数据上算法的AUC指标明显优于其他方法。同样,表 2是各种算法在不同稀疏度下对可见光高光谱图像的目标检测性能AUC指标。从表 2可以直观地看出,基于Kruskal分解的稀疏和稀疏匹配子空间检测方法要比原始光谱的稀疏和稀疏匹配子空间检测效果好,而稀疏匹配子空间方法相对于原始稀疏检测在原始光谱、拉普拉斯联合检测、联合稀疏检测及Kruskal分解优化上检测效果都明显得到提高,因此本文提出的Kruskal SMSD方法在AUC指标上是最优的。
| 稀疏度L | Spectral | Laplacian | Joint | Kruskal | ||||
| Sparse | SMSD | Sparse | SMSD | Sparse | SMSD | Sparse | SMSD | |
| 1 | 0.624 4 | 0.900 2 | 0.812 5 | 0.849 5 | 0.902 5 | 0.921 3 | 0.900 0 | 0.961 4 |
| 2 | 0.604 4 | 0.879 0 | 0.816 3 | 0.829 3 | 0.880 7 | 0.921 9 | 0.895 8 | 0.961 3 |
| 3 | 0.610 7 | 0.854 8 | 0.843 6 | 0.841 8 | 0.91 48 | 0.932 0 | 0.893 8 | 0.960 1 |
| 4 | 0.621 5 | 0.838 9 | 0.853 7 | 0.845 5 | 0.922 0 | 0.936 9 | 0.892 4 | 0.957 0 |
| 5 | 0.619 0 | 0.827 3 | 0.912 7 | 0.916 0 | 0.937 5 | 0.949 9 | 0.891 2 | 0.954 5 |
| 6 | 0.617 2 | 0.814 6 | 0.874 5 | 0.913 6 | 0.941 2 | 0.952 9 | 0.890 3 | 0.951 0 |
| 7 | 0.624 5 | 0.801 2 | 0.895 9 | 0.915 4 | 0.938 5 | 0.948 4 | 0.889 6 | 0.947 4 |
| 8 | 0.621 2 | 0.788 0 | 0.892 0 | 0.917 5 | 0.933 4 | 0.942 0 | 0.887 7 | 0.944 2 |
| 9 | 0.620 1 | 0.777 7 | 0.888 1 | 0.919 3 | 0.936 3 | 0.945 5 | 0.884 9 | 0.940 5 |
| 10 | 0.618 5 | 0.764 0 | 0.893 1 | 0.921 4 | 0.933 6 | 0.943 9 | 0.884 4 | 0.937 1 |
| 11 | 0.627 7 | 0.756 8 | 0.895 7 | 0.920 9 | 0.933 0 | 0.943 0 | 0.885 4 | 0.934 0 |
| 12 | 0.624 8 | 0.742 6 | 0.901 7 | 0.921 7 | 0.930 4 | 0.939 9 | 0.883 9 | 0.930 0 |
| 13 | 0.631 5 | 0.730 2 | 0.908 5 | 0.923 6 | 0.926 4 | 0.935 7 | 0.883 2 | 0.927 5 |
| 14 | 0.632 7 | 0.724 1 | 0.912 2 | 0.924 9 | 0.919 1 | 0.926 9 | 0.881 0 | 0.923 6 |
| 15 | 0.639 3 | 0.722 6 | 0.914 6 | 0.920 9 | 0.911 1 | 0.918 4 | 0.880 8 | 0.920 2 |
| 16 | 0.650 6 | 0.723 2 | 0.919 5 | 0.922 0 | 0.902 1 | 0.909 5 | 0.878 8 | 0.918 0 |
| 稀疏度L | Spectral | Laplacian | Joint | Kruskal | ||||
| Sparse | SMSD | Sparse | SMSD | Sparse | SMSD | Sparse | SMSD | |
| 1 | 0.791 9 | 0.928 4 | 0.523 6 | 0.957 8 | 0.693 0 | 0.920 4 | 0.703 0 | 0.971 1 |
| 2 | 0.774 0 | 0.853 0 | 0.525 2 | 0.948 1 | 0.712 7 | 0.706 0 | 0.736 4 | 0.944 7 |
| 3 | 0.758 3 | 0.827 6 | 0.636 8 | 0.923 9 | 0.689 2 | 0.703 8 | 0.734 4 | 0.908 9 |
| 4 | 0.744 1 | 0.808 2 | 0.723 1 | 0.892 8 | 0.659 8 | 0.695 8 | 0.731 1 | 0.877 5 |
| 5 | 0.754 1 | 0.790 8 | 0.839 8 | 0.838 5 | 0.639 1 | 0.674 6 | 0.728 3 | 0.841 8 |
| 6 | 0.759 7 | 0.776 7 | 0.845 4 | 0.776 8 | 0.630 1 | 0.645 6 | 0.724 9 | 0.818 9 |
| 7 | 0.777 3 | 0.776 2 | 0.846 3 | 0.755 8 | 0.653 4 | 0.649 4 | 0.721 2 | 0.796 3 |
| 8 | 0.783 5 | 0.773 1 | 0.844 4 | 0.737 5 | 0.686 3 | 0.670 4 | 0.718 6 | 0.779 0 |
| 9 | 0.787 2 | 0.769 7 | 0.842 7 | 0.723 0 | 0.719 3 | 0.698 3 | 0.714 9 | 0.758 2 |
| 10 | 0.796 7 | 0.773 2 | 0.841 6 | 0.717 2 | 0.764 7 | 0.741 5 | 0.713 4 | 0.746 8 |
| 11 | 0.797 7 | 0.769 1 | 0.841 2 | 0.712 7 | 0.793 4 | 0.770 8 | 0.712 0 | 0.731 9 |
| 12 | 0.800 7 | 0.770 6 | 0.840 1 | 0.708 9 | 0.803 0 | 0.783 7 | 0.711 8 | 0.719 5 |
| 13 | 0.802 0 | 0.771 4 | 0.839 8 | 0.704 6 | 0.813 1 | 0.798 4 | 0.710 5 | 0.707 1 |
| 14 | 0.804 3 | 0.772 2 | 0.839 8 | 0.701 2 | 0.818 7 | 0.807 5 | 0.709 1 | 0.700 4 |
| 15 | 0.807 2 | 0.775 1 | 0.839 1 | 0.694 0 | 0.830 3 | 0.822 3 | 0.707 7 | 0.694 7 |
| 16 | 0.800 9 | 0.771 8 | 0.838 8 | 0.685 8 | 0.834 3 | 0.827 0 | 0.706 8 | 0.688 5 |
AUC指标能表述检测算法在各个误警率下总的检测效果,而很多时候目标检测对误警率有严格限制,需要误警率低于某个限度,因此,这里给出了各方法在误警率小于10-2时的检测率曲线(即ROC曲线),此处针对分辨率较高的红外高光谱图像进行了试验,图 4为红外高光谱数据的试验结果,从图 4中可以看到基于Kruskal秩一分解的两种方法(Kruskal Sparse,Kruskal SMSD)在低误警率下检测率要明显高于其他方式,因此,Kruskal分解显示出明显的空间信息挖掘优势。
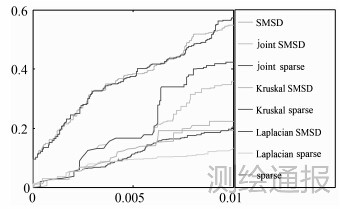 |
| 图 4 针对红外高光谱图像中各方法的ROC曲线 |
对于算法的性能,稀疏度的取值有着很大的影响,因此,分析了稀疏度对AUC的影响曲线(如图 5所示,其中,(a)为红外高光谱数据结果;(b)为可见光高光谱数据结果),从两个曲线图的分析中可以得到一致的结论:仅使用单纯的稀疏检测方法时,稀疏度的选择是无规律的,而其他方法都倾向于选择较小的稀疏度。这个现象可能存在的原因是,Kruskal分解和稀疏匹配子空间方法都倾向于将光谱向目标光谱转变,这样,通过使用较少的变换光谱即可实现目标检测。
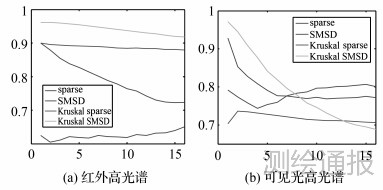 |
| 图 5 稀疏度影响曲线 |
由于一般算法的检测效果图中检测值分布不均匀,直接进行显示时,检测区域效果不太明显,因此这里对所有的检测图进行了取对数运算
式中,t为像素的检测值。式(20)中加1运算可以保证所有变换后的检测值都非负。
图 6和图 7分别是各个算法对两组数据的检测结果经式(20)变换后的效果图。从图 6对比可以看出,各种方法都可以检测出车辆目标区域。但是,对于车辆区域外的背景区域,非Kruskal分解的算法误判过多,不适合在低检测率下分析。而从图 7中可以看出拉普拉斯空谱约束和联合稀疏空谱约束检测错误区域过多,一般稀疏和Kruskal分解误判区域较小,因此,从空谱联合上讲,Kruskal分解是有优势的。
 |
| 图 6 各种算法对红外高光谱车辆目标检测效果 |
 |
| 图 7 各种算法对可见光高光谱车辆目标检测效果 |
针对高分条件下车辆目标检测问题,本文提出了一种基于Kruskal张量低秩分解的稀疏匹配子空间检测方法。该方法通过对局部高光谱图像三维空间进行低秩张量分解后的各分量的投影来挖掘高光谱数据的三维空谱联合一体信息;然后通过将匹配子空间的理论优势和稀疏分解的有效运行框架相结合;最后通过本文提出的稀疏匹配子空间检测模型对张量分解后的信息进行稀疏检测,由此提高了目标检测的精度,并降低了检测误警率。通过在高分辨率机载红外高光谱图像和高分辨率机载可见光高光谱图像数据中的测试,验证了本文算法的可行性和有效性,并将该方法与一般稀疏方法和空谱联合约束方法进行对比,验证了本文算法的优越性。
| [1] | HUCK A, GUILLAUME M. Asymptotically Cfar-Unsupervised Target Detection and Discrimination in HyperspectralImages with Anomalous-Component Pursuit[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(11): 3980-3991. |
| [2] | DAVIDSON C E, BEN-DAVID A. On the Use of Covariance and Correlation Matrices in Hyperspectral Detection[C]//2011 IEEE Applied Imagery Pattern Recognition Workshop (AIPR).Washington, DC: IEEE, 2011: 1-6. |
| [3] | KHAZAI S, SAFARI A, MOJARADI B, et al. An Approach for Subpixel Anomaly Detection in HyperspectralImages[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012,6(2): 769-778. |
| [4] |
 J, BOVOLO F, GÓMEZ-CHOVA L, et al. Semisupervised One-Class Support Vector Machines for Classification of Remote Sensing Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3188-3197. J, BOVOLO F, GÓMEZ-CHOVA L, et al. Semisupervised One-Class Support Vector Machines for Classification of Remote Sensing Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3188-3197.
|
| [5] | ZHAO L Y, ZHANG K, LI X R. Kernel Signature Space Orthogonal Projection for Target Detection in HyperspectralImagery[J]. Journal of Remote Sensing, 2011, 15(1): 13-28. |
| [6] | MATTEOLI S, ACITO N, DIANI M, et al. An Automatic Approach to Adaptive Local Background Estimation and Suppression in Hyperspectral Target Detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 790-800. |
| [7] | KWON H,GURRAM P. Optimal Kernel Bandwidth Estimation for Hyperspectral Kernel-Based Anomaly Detection[C]//Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium. Honolulu: IEEE, 2010: 2812-2815. |
| [8] | CHEN Y, NASRABADI N M, TRAN T D. Sparse Representation for Target Detection in HyperspectralImagery[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 629-640. |
| [9] | CHEN Y, NASRABADI N M, TRAN T D. Simultaneous Joint Sparsity Model for Target Detection in HyperspectralImagery[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 676-680. |
| [10] | CHEN Y, NASRABADI N M, TRAN T D. Kernel Sparse Representation for Hyperspectral Target Detection[C]//2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Munich: IEEE, 2012: 7484-7487. |
| [11] | KRUSKAL J B. Three-way Arrays: Rank and Uniqueness of Trilinear Decompositions, with Application to Arithmetic Complexity and Statistics[J]. Linear Algebra and Its Applications, 1977, 18(2): 95-138. |
| [12] | TUCKER L R. Some Mathematical Notes on Three-Mode Factor Analysis[J]. Psychometrika, 1966, 31(3): 279-311. |
| [13] | KIERS H A L. Towards a Standardized Notation and Terminology in Multiwayanalysis[J]. Journal of Chemometrics, 2000, 14(3): 105-122. |
| [14] | ZHANG T, GOLUB G H. Rank-one Approximation to High Order Tensors[J]. SIAM Journal on Matrix Analysis and Applications, 2001, 23(2): 534-550. |
| [15] | CHEN Y, NASRABADI N M, TRAN T D. HyperspectralImage Classification Using Dictionary-based Sparse Representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3973-3985. |
| [16] | SUN J M, TAO D C, PAPADIMITRIOU S, et al. Incremental Tensor Analysis: Theory and Applications[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2008, 2(3): 11. |
| [17] | TROPP J A, GILBERT A C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. |
| [18] | DAI W, MILENKOVIC O. Subspace Pursuit for Compressive Sensing Signal Reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249. |
| [19] | IEEE. 2013 IEEE GRSS Data Fusion Contest[EB/OL].2012-02-03.[2013-01-06].http://sites.ieee.org/spotlight/ieee-grss-announces-plans-for-2013-data-fusion-contest/. |
| [20] | IEEE. 2014 IEEE GRSS Data Fusion Contest[EB/OL].2010-05-05.[2011-06-07].http://www.grss-ieee.org/community/technical-committees/data-fusion/data-fusion-contest/. |