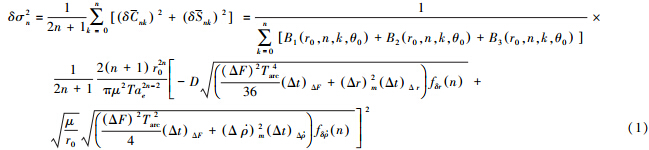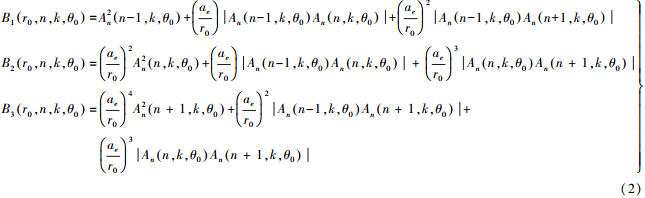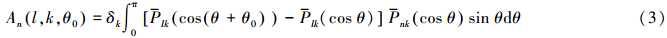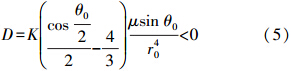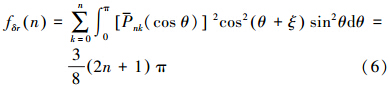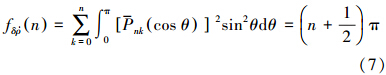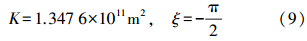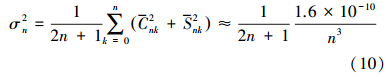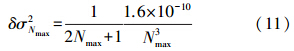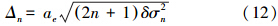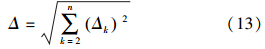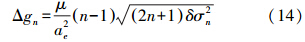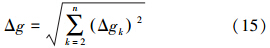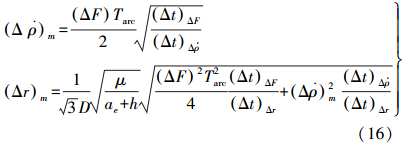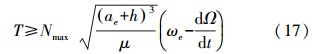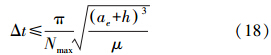2. 清华大学航天航空学院,北京 100084
一、引 言
重力场是地球的基本物理场,在地球科学研究、国土资源勘探和地质灾害预报等方面具有重要应用,历来是大地测量学研究的核心问题。随着航天技术的发展,卫星重力场测量以其全球高覆盖率、全天候、不受地缘政治和地理环境影响等独特优势,受到了越来越多的重视,在理论研究和工程实践上均取得了长足发展,已成为获取全球重力场模型的最有效手段[1, 2]。
根据观测数据的不同,卫星重力场测量可以分为轨道摄动、低低星星跟踪和重力梯度3种原理[3]。其中,轨道摄动原理适宜于低阶重力场测量,它的主要观测数据是卫星摄动轨道;低低星星跟踪原理适宜于中高阶重力场测量,它的主要观测数据是两个低轨卫星之间的距离及其变化率;重力梯度原理适宜于高阶重力场测量,它的主要观测数据是重力梯度值。已成功实施或正在研制的重力卫星均采用了以上测量原理或其组合,如CHAMP卫星利用轨道摄动原理恢复低阶重力场[4],GRACE、GRACE Follow-on、NGGM卫星同时利用了轨道摄动和低低星星跟踪原理恢复中高阶重力场[5, 6, 7],GOCE卫星分别利用轨道摄动和重力梯度原理恢复低阶和高阶重力场[8]。虽然这3种原理适宜于不同的重力场测量频段,但是重力场测量有效阶数和精度最终要取决于重力卫星的载荷指标。在针对中高阶重力场测量的低低星星跟踪和重力梯度方式下,以目前的载荷性能指标分析可知,低低星星跟踪测量完全可以达到甚至超过重力梯度的测量水平。为此,2007年在荷兰召开的“未来重力卫星测量”专题研讨会上决定,目前国际重力卫星继续采用低低星星跟踪重力场测量方式,同时考虑提高改善系统参数以提高重力场测量性能[9]。
针对低低星星跟踪重力场测量系统轨道参数和载荷指标设计,传统上主要采用数值模拟法分析系统参数对重力场测量性能的影响,进而确定系统设计参数。但是,重力场测量数值模拟对计算机性能要求非常高,计算时间非常长,不利于分析系统参数对重力场测量的影响规律,不便于进行系统参数的优化设计。为克服这一缺陷,本文从能量守恒原理出发,建立了分析低低星星跟踪重力场测量性能的解析方法,可以快速获取重力场测量有效阶数、大地水准面误差和重力异常误差等重力场测量性能,确定系统参数对重力场测量的影响规律,对低低星星跟踪重力卫星系统参数设计具有重要的指导意义。
二、星星跟踪重力场测量性能的解析计算模型基于频谱分析方法,得到星星跟踪重力场测量的阶误差方差为
其中上述公式中的物理参数说明见表 1。
| 参数名称 | 参数涵义 | 参数名称 | 参数涵义 |
| δσ2n | 阶误差方差 | δCnk,δSnk | 位系数误差 |
| r0 | 卫星地心距 | θ0 | 两个卫星之间的地心矢量夹角 |
| ae | 地球平均半径 | μ | 地球万有引力常数 |
| h | 卫星轨道高度 | Tarc | 积分弧长 |
| ΔF | 非引力干扰 | ΔtΔF | 非引力干扰的采样间隔 |
| Δrm | 卫星定轨位置误差 | ΔtΔr | 卫星轨道数据采样间隔 |
| Δm | 星间距离变化率误差 | ΔtΔ | 星间距离变化率误差采样间隔 |
| T | 重力场测量的总时间 |
利用式(1)—式(9)给出的阶误差方差可以确定重力场测量的有效阶数、大地水准面误差和重力异常误差等重力场测量性能。
根据Kaula准则,地球重力场模型的阶方差[10]为
阶误差方差δσ2n是n的增函数,阶方差σ2n是n的减函数。随着n的增加,当δσ2n等于σ2n时,认为达到重力场反演的最高阶数Nmax,即
由式(11)得到n阶大地水准面的阶误差为
进而得到n阶大地水准面的累积误差为
由式(11)得到n阶重力异常的阶误差为
进而得到n阶重力异常的累积误差为
三、重力场测量性能解析模型验证
GRACE卫星采用了星星跟踪重力场测量原理,它由500 km轨道高度上的两颗卫星组成跟飞编队,星间距离为(220±50) km,轨道倾角为89°,利用GPS接收机实现厘米级精密定轨,利用加速度计以1.0×10-10m/s2的精度实现非引力干扰测量,利用K/Ka波段电磁波以1 μm/s的精度实现星间距离变化率测量[11, 12, 13]。GRACE重力场测量的有效阶数为160左右,相应的大地水准面累积误差为分米级[14]。可以将GRACE卫星系统参数代入本文建立的星星跟踪重力场测量性能解析计算模型中,计算重力场测量的有效阶数和大地水准面误差,进而与GRACE卫星重力场测量的实际性能相比,可以验证本文所建立解析模型的正确性。
基于GRACE卫星系统参数,利用解析模型计算得到重力场测量的阶误差方差和大地水准面误差,如图 1—图 2所示。
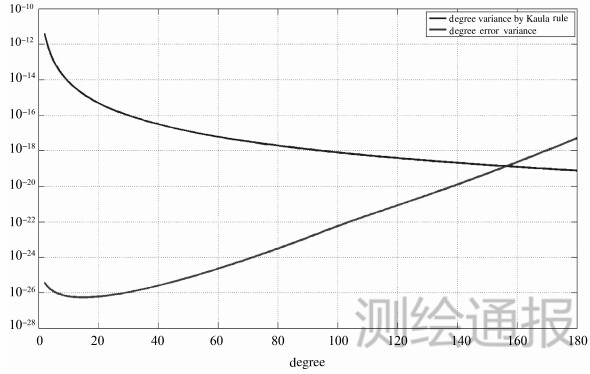 |
| 图 1 重力场测量的位系数阶误差方差 |
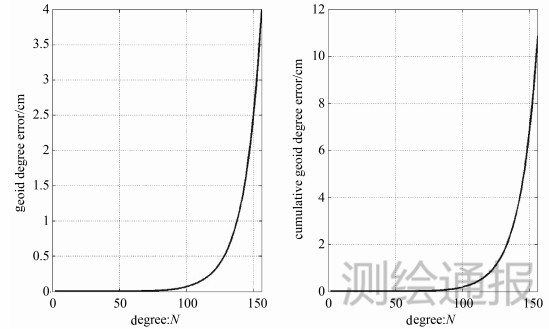 |
| 图 2 重力场测量的大地水准面阶误差及其累积误差 |
由图 1和图 2可知,利用解析模型计算得到的重力场测量有效阶数为156,相应的大地水准面累积误差为11 cm,与GRACE卫星实际重力场测量性能相吻合,从而验证了本文所建立的星星跟踪重力场测量性能解析模型的正确性。
四、卫星系统参数对重力场测量性能的影响机理下面基于式(1)—式(15)分析星星跟踪重力卫星系统参数对重力场测量性能的影响机理,其中标称参数见表 2;进而,根据系统参数的影响机理,提出星星跟踪重力场测量卫星任务优化设计方法,实现地球重力场测量性能的最大化。
| 参数名称 | 参数值 | 参数名称 | 参数值 |
| 轨道高度 | 300 km | 星间距离 | 100 km |
| 星间距离变化率测量误差 | 1.0×10-8m/s | 星间距离变化率数据采样间隔 | 30 s |
| 卫星定轨误差 | 5 cm | 卫星定轨数据采样间隔 | 30 s |
| 非引力干扰误差 | 1.0×10-12 m/s2 | 非引力干扰抑制间隔 | 30 s |
| 重力场测量总时间 | 6 months |
在仅改变轨道高度的情况下,得到重力场测量的最高阶数及相应的大地水准面阶误差,如图 3所示。由图 3可知,重力场测量性能随轨道高度的降低而迅速增加。由此说明,重力信号随轨道高度的增加而迅速衰减,轨道高度越低,越有利于敏感重力信号。
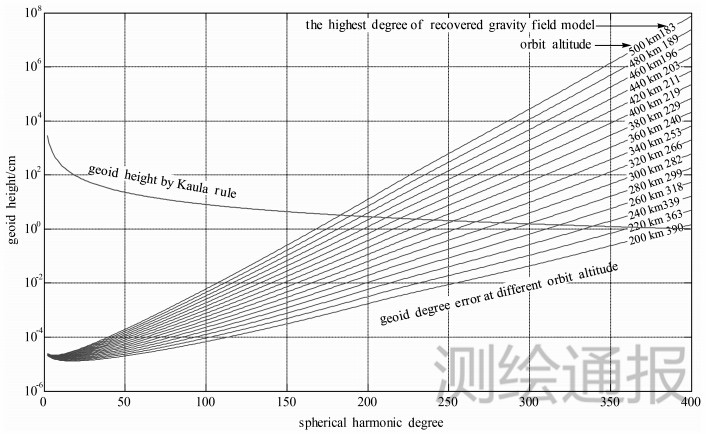 |
| 图 3 不同轨道高度下的重力场测量性能 |
在仅改变星间距离的情况下,得到卫星重力测量的大地水准面阶误差,并在不同的阶数范围内将其累积,如图 4所示,其中标注了与所累积阶数范围对应的空间分辨率。由图 4可知,使第n阶重力信号测量误差最小的星间距离为π(ae+h)/n,这恰好等于阶数n所对应的空间分辨率。这是因为当两星距离为π(ae+h)/n时,它们始终相距第n阶引力波长的一半,其测量信号之差的信噪比最高,从而使测量误差最小。
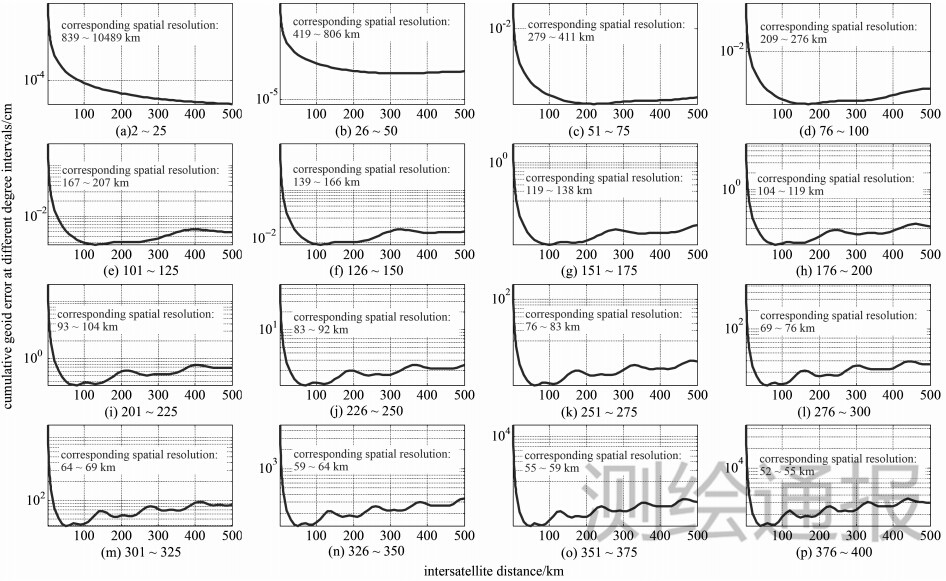 |
| 图 4 大地水准面累积误差随轨道高度的变化 |
星间距离变化率测量误差、卫星定轨误差和非引力干扰误差反映了重力卫星载荷的引力敏感能力,原则上它们越小越有利于获取两个内卫星在纯地球引力作用下的动力学信息,从而越有利于提高重力场测量性能。但是,由于重力场测量是这3项误差综合作用的结果,只有使3项测量误差相互匹配,也就是说使它们在阶误差方差中所占的比重一致时,才能最大限度地发挥各个载荷的测量能力,实现重力信息获取的最大化。根据匹配要求得到这3项误差在数量上满足
4. 总任务时间和测量数据采样间隔为获取全球重力场模型,需要使重力卫星测量数据覆盖全球,分为沿经度和纬度方向的覆盖测量。沿经度方向的覆盖测量是指在总任务时间内,重力卫星运动轨迹在东西方向上的间隔不大于重力测量的空间分辨率,由此得到对总任务周期T的下限约束为
式中,Nmax是重力场测量的最高阶数;ωe是地球自转角速度;dΩ/dt是摄动作用下升交点赤经随时间的变化率。
沿纬度方向的覆盖测量是指在一个轨道周期内,相邻两次数据采样的间隔不大于重力测量的空间分辨率,由此得到对数据采样率的上限约束为
在满足全球覆盖测量要求的条件下,总任务时间越长,测量数据采样间隔越小,越有利于降低测量误差的影响,提高重力场测量性能。
由此,得到了高分辨率星星跟踪重力卫星任务优化设计方法为:
1)轨道高度尽可能低,同时应与总任务时间、数据采样间隔相协调,满足全球覆盖测量要求,见式(17)和式(18);
2)星间距离选取为重力场测量阶数对应的空间分辨率;
3)星间测量误差、卫星定轨误差和非引力干扰误差越小越好,但应满足误差匹配关系,见式(16);
4)数据采样间隔和总任务时间满足覆盖测量要求,见式(17)和式(18)。
五、结束语
本文建立了星星跟踪重力场测量性能的解析计算模型,并利用GRACE卫星参数及其实际重力场测量性能验证了模型的正确性;基于该解析模型,揭示了轨道高度、星间距离、定轨误差、星间距离变化率测量误差、非引力干扰确定误差、任务测量时间和数据采样间隔等参数对重力场测量影响的复杂机理,进而提出了星星跟踪重力场测量任务优化设计方法,为合理设计重力卫星系统参数、实现重力场测量性能最大化提供了理论指导。
| [1] | 宁津生。跟踪世界发展动态致力地球重力场研究[J]. 武汉大学学报:信息科学版,2001, 26(6): 471-474, 486. |
| [2] | 宁津生。卫星重力探测技术与地球重力场研究[J]. 大地测量与地球动力学,2002, 22(1): 1-5. |
| [3] | 谷振丰,刘红卫,王兆魁,等。基于引力位系数相对权重的卫星重力场测量分析[J]. 地球物理学进展,2013, 28(1): 17-23. |
| [4] | REIGBER C, SCHWINTZER P, NEUMAYER K H, et al. The CHAMP-only Earth Gravity Field Model EIGEN-2[J]. Advances in Space Research, 2003, 31(8): 1883-1888. |
| [5] | TAPLEY B, RIES J, BETTADPUR S, et al. GGM02-An Improved Earth Gravity Field Model from GRACE[J]. Journal of Geodesy, 2005, 79(8): 467-478. |
| [6] | LOOMIS B D, NEREM R S, LUTHCKE S B. Simulation Study of a Follow-on Gravity Mission to GRACE[J]. Journal of Geodesy, 2012, 86(5): 319-335. |
| [7] | CESARE S, AGUIRRE M, ALLASIO A, et al. The Measurement of Earth's Gravity Field after the GOCE Mission[J]. Acta Astronautica, 2010, 67(7-8): 702-712. |
| [8] | MUZI D, ALLASIO A. GOCE: The First Core Earth Explorer of Esa's Earth Observation Programme[J]. Acta Astronautica, 2003, 54(3): 167-175. |
| [9] | KOOP R, RUMMEL R. The Future of Satellite Gravimetry[R]. Noordwijk, The Netherlands:ESTEC,2007. |
| [10] | KAULA W M. Theory of Satellite Geodesy: Applications of Satellites to Geodesy[M]. Mineola, New York: Dover Publication, Inc., 2000. |
| [11] | KIM J, LEE S W. Flight Performance Analysis of GRACE K-band Ranging Instrument with Simulation Data[J]. Acta Astronautica, 2009, 65(11-12): 1571-1581. |
| [12] | KANG Z, NAGEL P, PASTOR R. Precise Orbit Determination for GRACE[J]. Advances in Space Research, 2003, 31(8): 1875-1881. |
| [13] | KIM J, TAPLEY B D. Error Analysis of a Low-low Satellite-to-Satellite Tracking Mission[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(6): 1100-1106. |
| [14] | BALMINO G. Gravity Field Recovery from GRACE: Unique Aspects of the High Precision Inter-satellite Data and Analysis Methods[J]. Space Science Reviews, 2003, 108(1-2): 47-54. |