2. 武汉市测绘研究院,湖北 武汉 430022
一、引 言
近年来,GIS应用在公共卫生健康及空间流行疾病领域发展迅速,并为其提供准确有效的分析及制图可视化工具。GIS可支持疾病制图、定点分析、人口地理描述、空间统计分析和建模[1],而疾病具有空间聚集分布现象,且聚集现象意味其已经在一定区域内建立了较为有效的传播途径,可作为疾病由局部散发性疫情向大规模暴发流行转变的重要预警信号[2]。因此,充分利用疾病的时间与空间信息,将GIS时空聚集分析及可视化技术应用于空间流行疾病领域,就可以对疫情实时监控并进行预测,以直观的方式在疾病监测、资源分配等方面为卫生行政部门提供科学参考。
因有效的抗结核疫苗的全面普及,中国结核病发病率有所下降,但是在发展中国家,结核病仍然是公众健康的主要危险之一,在我国也是主要传染病之一[3]。因此本文以全国省级肺结核发病数据为研究对象,使用GIS的可视化技术,基于空间聚集分析,对疾病的空间聚集情况进行探寻与分析,并依据时间序列对疾病进行分析预测,最后,以时空扫描统计方法对疾病发生的时间、空间结合分析,所得结果表明该时空聚集分析方法可靠,可为公共卫生决策提供参考建议。
二、疾病数据时空聚集方法疾病聚集研究是为了寻找空间或时空上的疾病发生风险明显高的地区,有助于疾病预警及资源合理分配。本文研究疾病时空聚集的方法如图 1所示,对疾病数据依次进行空间聚集分析、时间序列预测分析及时空扫描分析,对疾病的发病情况进行深入的研究。
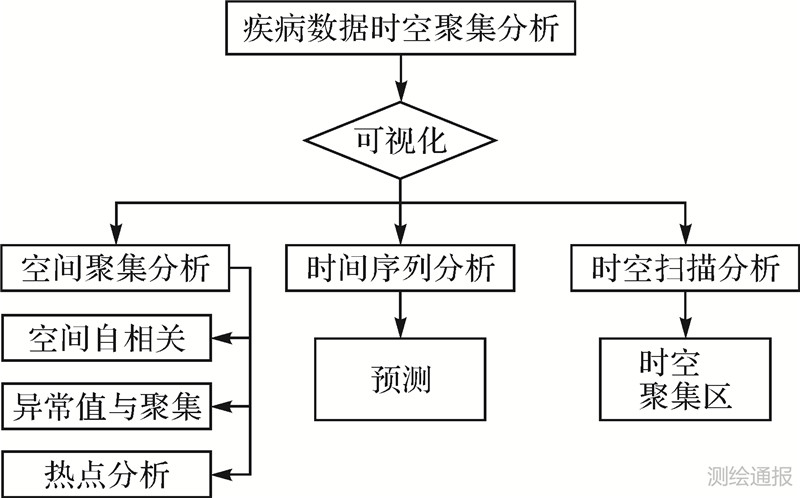 |
| 图 1 疾病数据时空聚集分析方法 |
空间聚集分析主要包括全局自相关分析、局部自相关分析及热点分析。其中,全局自相关分析采用Moran′s I指数;当Moran′I指数为0时,说明无聚集;当Moran′I指数大于0时,则正空间自相关;反之,空间负自相关。Moran′I的统计检验P值由蒙特·卡罗随机试验得到。当区域数据具有空间自相关性后,可进行局部自相关性检验,它通过对每个区域进行Moran′I指数统计,探测局部的聚集情况,通常采用局部空间关联指标(LISA)[4],可探索局部自相关性,或通过Moran散点图发现异常值。热点分析是对每个要素计算Getis-Ord Gi* 统计[5],Gi* 统计是局部聚集的指标,代表分布地区的“中心”,通过对比局部自相关估计与全局平均水平,在空间上发现热点。
2. 时间序列预测ARIMA模型为了研究事物的动态演变规律,按某种(相等或不相等)时间间隔对客观事物进行实时观察,所得观察结果X1、X2、…、Xi被称作时间序列,其数学本质是随机过程的一次具体实现[6]。时间序列时域分析基本模型主要有指数平滑方法及ARIMA模型,而在医学范畴内ARIMA模型应用广泛[7, 8]。ARIMA自回归综合移动平均模型也称box-jenkins模型,基本思想是将预测对象随时间推移而形成的数据视为一组依赖于时间t的随机变量[9],然后用数学模型来描述变量序列,其建模过程如图 2所示。
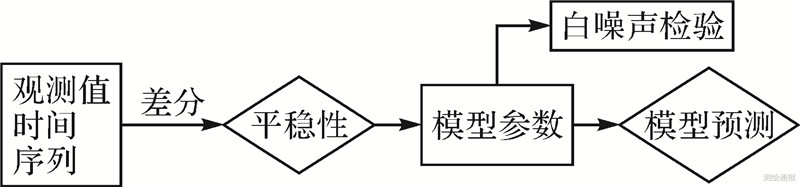 |
| 图 2 ARIMA模型建模过程 |
时空扫描统计是时空事件聚类分析方法中的一种,它是由Kulldorff在空间扫描统计基础上扩展得到的[10],旨在探索时空范围的聚集性与比较随机分布模式,是否显著增加,并确定聚集性最可能异常的时空事件集合[11]。时空扫描统计方法在流行病时空聚集研究领域应用广泛[12, 13],能够对流行病发病的时间、地点及其规模的大小进行深入分析,从而实现流行病爆发的早期识别[14]。其基本思想是首先采用一个以空间距离定义半径、时间长度定义高度的圆柱体作为二维扫描窗口,扫描每一个时空事件,然后在每个窗口根据泊松分布,以人口数与总发病数计算理论发病数,通过窗口内外理论与实际发病人数构造统计量对数似然比(LLR),用LLR来描述扫描窗口内发病数的异常程度。最后,基于蒙特卡罗模拟法生成的随机数据集,以相同方法计算LLR值,对窗口进行显著性检验。
三、疾病数据可视化疾病制图在空间流行病领域中发挥很大的作用,可以发现疾病的潜在危险区域,协助病因学研究,分析疾病地理分布情况,合理分配医疗资源,对疾病扩散起一定的预防作用。在疾病制图及空间聚集分析时,考虑到区域人口总量的变异性,及区域发病率比患病人数更能准确地反映疾病真实的空间分布[15],使用发病率指标作为试验数据。发病率是一段时间之间出现的新患病人数与总人口数的百分比,计算方法为

本文研究以全国省级肺结核发病数据为研究对象,考虑到空间的连续性及数据获取情况,文中暂不考虑海南、香港、澳门、台湾的发病情况,因此下文中分析过程将不包括上述地区。整理数据,得出各省2005—2012年平均肺结核发病率数据,对该数据进行可视化分析,得出整体上各地区不同的发病情况,如图 3所示。
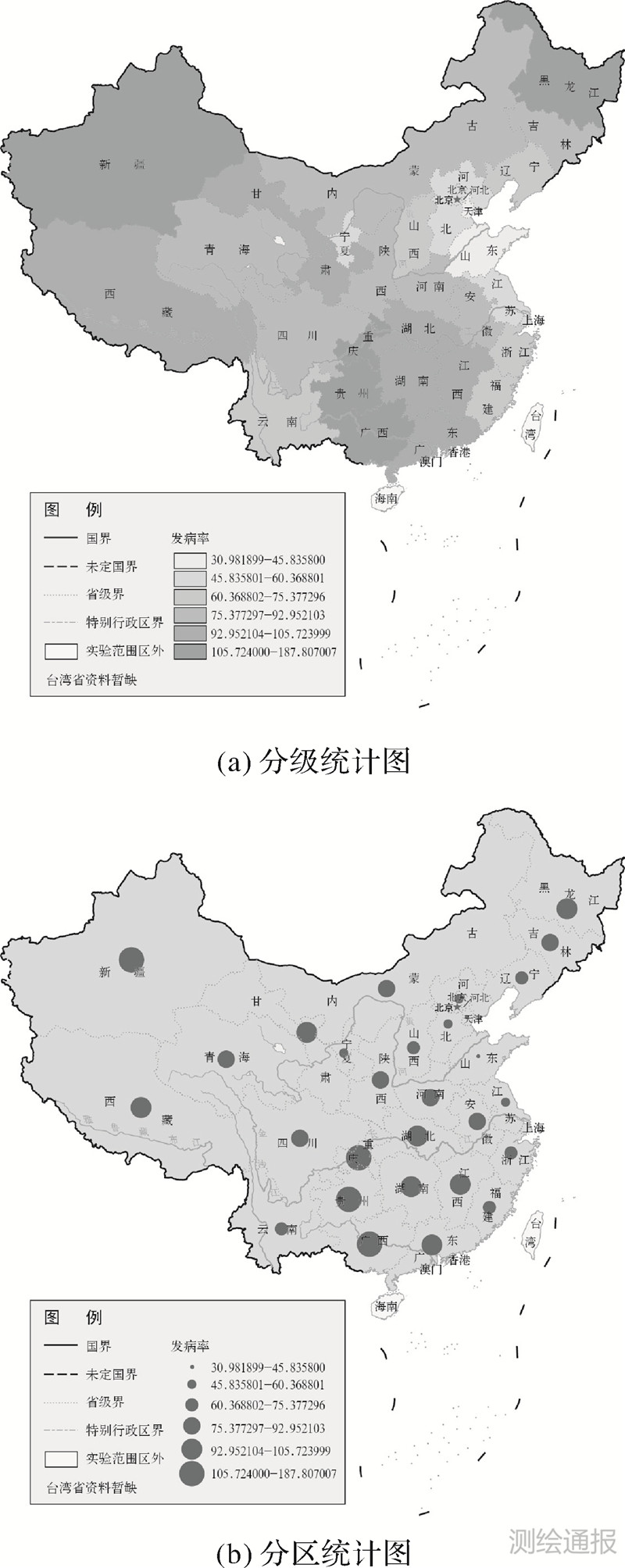 |
| 图 3 全国2005—2012各省年平均肺结核发病率统计图 |
考虑到分级图受省级边界的限制,发病率统计图不够连续光滑,使用插值方法生成发病率地形图,如图 4所示。地学统计克里金插值法不同于其他确定性插值方法,它考虑空间变异性,并可将随机因素及相关因素考虑进来,这样疾病制图的效果更准确[16]。
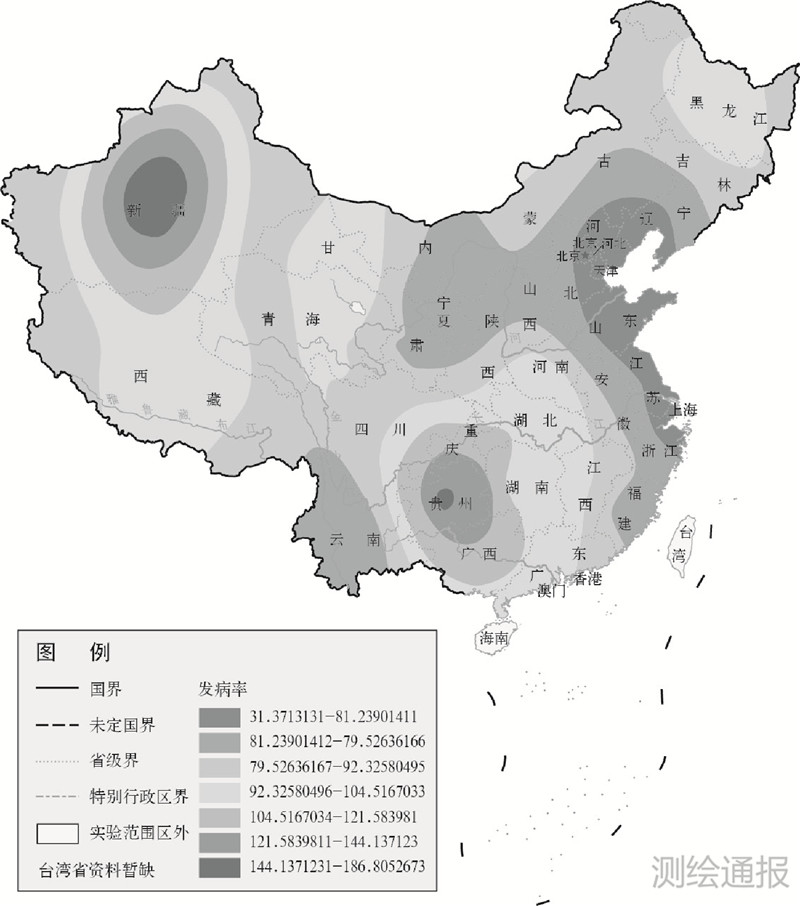 |
| 图 4 全国2005—2012各省年平均肺结核发病率克里金插值图 |
结合分析图 3、图 4,可初步判断新疆、贵州广西的两部分区域为高发病率区域,北京天津及沿海区域为低发病率区域。
四、疾病数据时空聚集分析 1. 空间聚集分析ArcGIS“空间统计”工具箱中的工具可以对空间分布的显著特征进行汇总,识别具有统计显著性的空间聚类(热点/冷点)或空间异常值,评估聚类或离散的总体模式并建立空间关系模型。本文将使用该工具箱工具进行一系列空间聚集分析。
(1) 空间自相关分析
Globe Moran′s I指数代表了全局发病率的空间自相关性及分布模式,Z得分和P值都是统计显著性的度量,用于逐要素判断是否拒绝零假设。若Moran′s I指数大于0,且P<0.05,Z>1.96,说明研究区域具有空间相关性,其分布是聚集型分布。选取2005—2012年肺结核发病率数据进行全局空间自相关分析,部分结果见表 1,表明全国发病率数据呈聚集型分布,并非随机分布。
| 年份 | Moran′s I 指数 | P值 | Z-score值 | 分布 |
| 2005 | 0.355 144 | 0.000 000 | 5.072 096 | 聚集 |
| 2007 | 0.348 283 | 0.000 000 | 5.069 199 | 聚集 |
| 2009 | 0.338 019 | 0.000 000 | 4.946 951 | 聚集 |
| 2011 | 0.379 246 | 0. 000 000 | 5.417 108 | 聚集 |
(2) 聚类和异常值分析
Anselin Local Moran′s I 统计量可识别具有统计显著性的热点、冷点和空间异常值,选取2005—2012年肺结核发病率数据进行聚类和异常值分析,部分结果如图 5所示,HH代表高值聚集类,LL代表低值聚集类,HL代表高值要素而四周围绕的是低值要素,LH代表低值要素而四周围绕的是高值要素。由图 5可知,2005年和2007年,贵州、广西、重庆为高发病率聚集区,北京、天津等为低发病率聚集区;2009年高发病率聚集区发生变化,新增新疆、西藏地区,广西、重庆地区不明显,低发病率聚集区增加江苏及上海;2011年新疆、西藏和贵州为高发病率聚集区,低发病率聚集区大致不变。总体上,随着时间变化,高发病率聚集区发生改变,结合原发病率数据,新疆地区发病率高,西藏地区2009年和2011年发病率骤升,因此与新疆地区形成新高发病率聚集区;广西、重庆2007年后发病率随时间大致呈下降趋势。
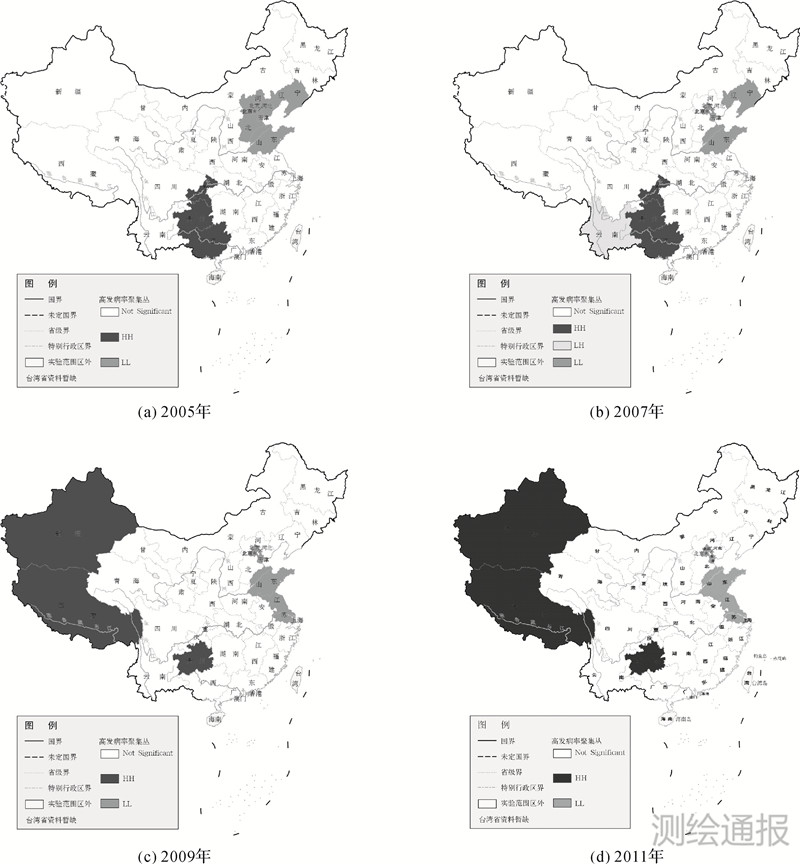 |
| 图 5 2005—2011年全国肺结核发病率聚类及异常值分析 |
(3) 热点分析
热点分析用于识别具有统计显著性的高值(热点)和低值(冷点)的空间聚类,以Z得分进行制图。由图 6可知,随着时间变化,热点区域有所改变,其分析结果与聚类分析大体一致,2005年与2007年,新疆、贵州、广西等区域为热点区域,北京、天津、上海等为冷点区域,随着时间变化,2009年与2011年新增西藏为热点区域,冷点区域基本一致。
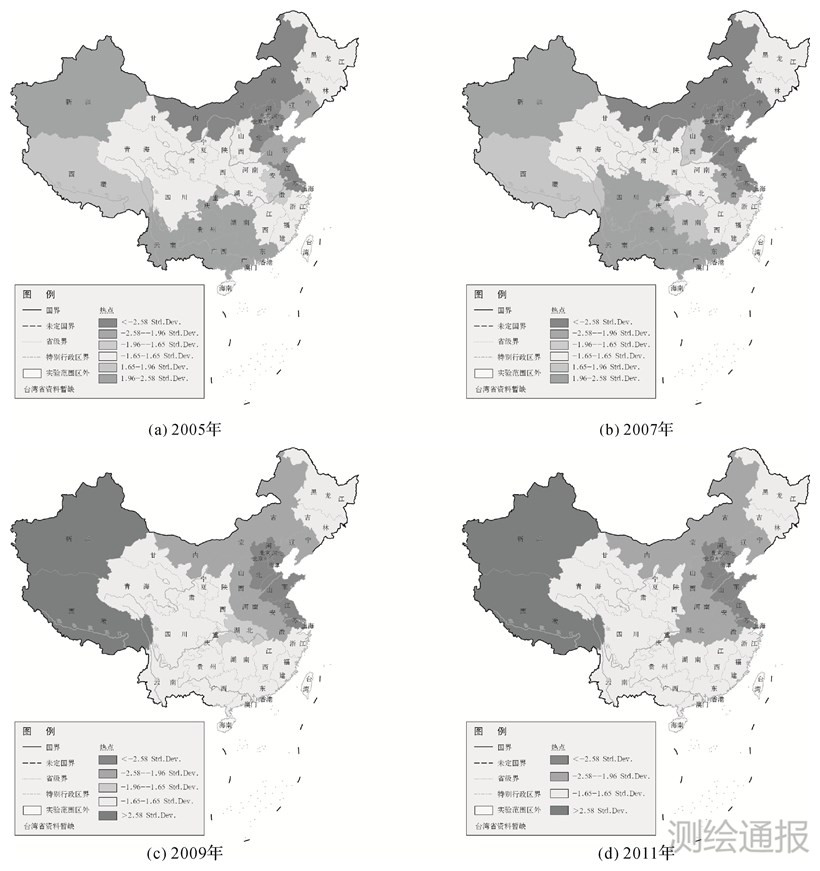 |
| 图 6 2005—2011年全国肺结核发病率的热点分析 |
全国发病率如图 5(a)所示,全国年发病率在2005年达到最高值,之后呈递减趋势。以发病率热点省份新疆和贵州为例,2005—2012年以月份为时间间隔,序列图如图 7所示,可知发病率具有年周期性。新疆月发病率在2007年1月份达到最高值,年内大致呈下降趋势,偶见年底反弹;贵州月发病率在2008年1月份达到最高值,年内大致呈下降趋势。新疆和贵州年内发病率趋势大体一致,可知年初为高发病率时期,推测冬季初春为高发病时段。
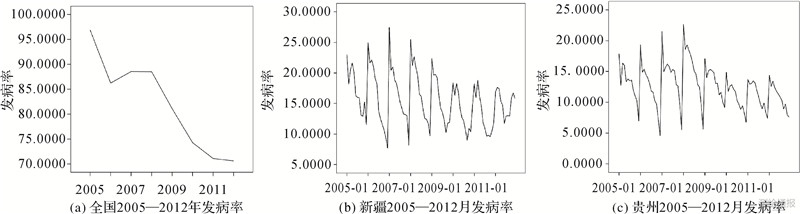 |
| 图 7 发病率时间序列图 |
在已有大量时间属性的数据下,可对贵州时间序列进行预测。选择时间序列ARIMA模型,经过参数调试,选用参数模型ARIMA(1,0,0)(1,0,0),所得Q统计量值为0.473>0.05,说明残差彼此独立,且残差基本符合零均值正态分布,因此残差通过白噪声检验,说明该模型比较合理。得出预测图如图 8所示,所得预测结果见表 2,其中UCL为高值置信区,LCL为低值置信区,预测值均在置信区,预测值可靠。
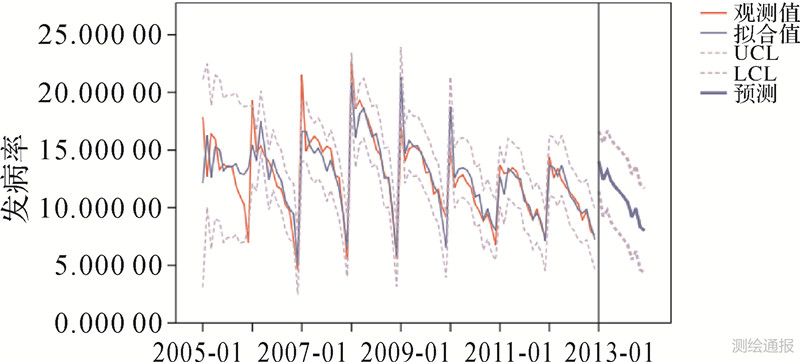 |
| 图 8 贵州2013年月发病率预测图 |
| 模型预测 | 1月 | 2月 | 3月 | 4月 | |
| 发 病 率 | 预测 | 14.048 06 | 12.433 32 | 13.228 87 | 12.307 88 |
| UCL | 16.652 94 | 15.630 36 | 16.687 27 | 15.891 36 | |
| LCL | 11.443 19 | 9.236 29 | 9.770 46 | 8.724 39 | |
使用软件SaTScan v9.3.1 ,对2005—2012年全国省份年肺结核患病数据进行回顾性时空扫描分析,结果见表 3,肺结核发病在时间和空间上存在明显的聚集性。最可能聚集区域为新疆、贵州、广西、重庆等组成的区域范围,其LLR值高于其他聚集区域,聚集时间为2005—2008年。另外发现,黑龙江在2005—2008年构成次聚集区域,表明在该时间段内发病异常增多,呈聚集性分布。同时,内蒙古2005年发病呈聚集型分布,表明2005年为疾病高发时段。由时空扫描分析得出时空上最可能聚集区域,如图 9所示。
| 聚集区 | 时间 | 聚集省份 | 实际病例数 | 理论病例数 | RR值 | LLR值 | P值 |
| 1 | 2005—2008 | 新疆、贵州等 | 2 540 350 | 1 933 149. 14 | 1.45 | 115 190.25 | <0.000 01 |
| 2 | 2005—2008 | 黑龙江 | 169 622 | 125 953.72 | 1.35 | 6 933.63 | <0.000 01 |
| 3 | 2005 | 内蒙古 | 25 703 | 19 650.33 | 1.31 | 851.06 | <0.000 01 |
 |
| 图 9 2005—2012年全国肺结核发病时空聚集情况 |
疾病制图作为疾病数据的可视化方法之一,能够在空间上反映疾病的分布情况,并将统计分析结果更加直观地表达出来。本文以全国省级肺结核患病数据为源数据,使用全局空间自相关、局部自相关分析、时间序列预测分析及时空扫描分析方法,对全国肺结核疾病的时空聚集情况进行分析及可视化。试验结果为全局疾病呈聚集分布,空间上确定高发病率区及低发病率区,时间上确定高发病时间段,结合时间与空间,寻找时空上高发病聚集区,分析结果具有一定的参考价值。本文时空聚集分析方法适用于分析疾病在时空上的聚集情况,分析结果可使相关医疗部门人员更深刻地认识疾病的发病情况,有利于发现重点防治区,加强对高发病区域的监测与预警,防止疾病暴发,并协助有所侧重地合理分配医疗资源,为疾病控制决策提供科学的参考依据。
| [1] | JACQUEZ G M. Spatial Analysis in Epidemiology:Nascent Science or a Failure of GIS?[J]. Journal of Geographical Systems, 2000, 2(1):91-97. |
| [2] | 张人杰,葛尓佳,张双凤,等.高致病性 H5N1禽流感全球分布地理信息系统时空分析[J].中国公共卫生,2014, 30(1):26-29. |
| [3] | 张俊辉,李晓松,叶运莉.我国肺结核病危险因素的 Meta 分析[J].现代预防医学,2010,37(2):207-209. |
| [4] | ANSELIN L. Local Indicators of Spatial Association-LISA[J]. Geographical Analysis, 1995, 27(2):93-115. |
| [5] | GETIS A, ORD J K. The Analysis of Spatial Association by Use of Distance Statistics[J]. Geographical Analysis, 1992, 24(3):189-206. |
| [6] | 王彤.医学统计学与 SPSS 软件应用[M].北京:北京大学医学出版社,2008:307. |
| [7] | 杨召,叶中辉,赵磊,等.ARIMA-BPNN 组合预测模型在流感发病率预测中的应用[J].中国卫生统计,2014, 31(1):16-18. |
| [8] | 王涛,苑新海,朱宗龙.ARIMA 时间序列在乙肝发病预测中的应用[J].中国卫生统计,2014,31(4):646-647. |
| [9] | 丁亚兴,张之伦,朱向军.自回归综合移动平均模型对天津市甲型肝炎发病预测[J].疾病监测,2008, 23(5):326-328. |
| [10] | KULLDORFF M, ATHAS W F, FEURER E J, et al. Evaluating Cluster Alarms:a Space-time Scan Statistic and Brain Cancer in Los Alamos, New Mexico[J]. American Journal of Public Health, 1998, 88(9):1377-1380. |
| [11] | 唐建波,邓敏,刘启亮.时空事件聚类分析方法研究[J].地理信息世界,2013,20(1):38-45. |
| [12] | ONOZUKA D, HAGIHARA A. Geographic Prediction of Tuberculosis Clusters in Fukuoka, Japan, Using the Space-time Scan Statistic[J]. BMC Infectious Diseases, 2007, 7(1):1-9. |
| [13] | 王强,高金彬,许静,等.运用时空扫描统计量分析江苏省高邮市钉螺时空分布中[J].中国寄生虫学与寄生虫病杂志,2014, 32(2):110-115. |
| [14] | 肖辉,肖革新.时空扫描统计量在细菌性痢疾监测数据分析中的应用[J].中国食品卫生杂志,2014, 26(1):83-87. |
| [15] | ROBINSON T, STEVENSON M, STEVENS K B, et al. Spatial Analysis in Epidemiology[M]. New York:Oxford University Press, 2008:35. |
| [16] | ZHONG S, XUE Y, CAO C, et al. Explore Disease Mapping of Hepatitis B Using Geostatistical Analysis Techniques[C]// Berlin:Springer Berlin Heidelberg, 2005:464-471. |
| [17] | 郭云开,王杨.路域植被覆盖度时空变化遥感定量反演[J].测绘通报,2013(5):23-27. |
| [18] | 张健钦,邙晓宇,徐志洁,等.基于GIS的居民出行调查数据时空查询分析研究[J].测绘通报,2013(4):21-24. |


