引言

雷电灾害造成的损失包括直接的人员伤亡和经济损失，随着全球气候变化以及我国城市化进程的快速发展，雷电灾害对国民经济和人民生命财产造成的威胁也日益增大。因此，雷电灾害研究和风险评估工作越来越受到国家及有关部门的高度重视。由于雷灾资料的获取需要相关人员及时收集、整理、统计，极易出现漏报现象，这就会造成雷灾样本少、相关信息不够完整等现状，使得分析结果和实际的灾害风险具有一定的差距(成勤等，2016；余田野等，2019)。而信息扩散理论能够弥补信息的不足，可以对不同级别的雷灾风险进行定量化的风险计算，在雷灾样本较少的情况下得出较为合理的风险评估结果。

诸多研究发现：基于信息扩散技术的模糊风险评估模型能体现出风险评估的不确定性，便于决策时留有调整空间(Xu et al., 2009；杜子璇等，2012；王莺等，2013；魏道江等，2015；Wu et al., 2015)。二十世纪九十年代，美国气象部门提出将信息扩散理论应用于气候预测研究中(Lai and Gerald, 1990）。目前，该理论已在灾害风险分析中得到广泛应用(刘引鸽等，2005；张丽娟等，2009；刘亚彬等，2010；杜子璇等，2012；Liu et al., 2013)。例如：王莺等(2016)利用信息扩散理论对中国南方水旱灾害风险特征进行了分析；王学林等(2019)提出了一种基于信息扩散理论的南方双季早稻气象灾害风险评估的方法；王春扬等(2010)将信息扩散理论用于福建省重大雷电灾害风险预测；栾健等(2013)将信息扩散理论用于雷电天气关注度研究。这些研究结果对防灾减灾工作起到了一定的指导作用，同时现今有关雷电灾害风险分析及区划的研究工作已被大量报道(金晨路等，2011；程向阳等，2012；赵伟等，2014；吴安坤等，2015；朱浩等，2015；崔新强等，2021)，但将信息扩散理论应用于雷电灾害风险评估、风险区划的成果还较为少见，缺乏针对江苏省雷电灾害风险预测的研究。

为此，本文以信息扩散理论为依据建立雷电灾害风险评估模型，对雷电灾害进行集值化的模糊数学处理，以弥补雷电灾害领域数据信息的不足, 并深入挖掘雷电灾害中的潜在信息，以期为建筑工程规划、选址以及雷电灾害风险评估等提供参考和指导。

1 研究方法与资料来源

雷电灾害风险评估作为一种环境风险评估，可以借鉴其它环境自然灾害领域内合理的风险评估的研究成果。基于信息扩散理论的气象灾害风险评估模型，就是一种被大家广泛采用的分析方法。信息扩散是指为了弥补信息不足而考虑优化利用样本模糊信息的一种对样本进行集值化的模糊数学处理方法。该方法可以将一个有观测值的样本，变成一个模糊集，即将单值样本变成集值样本，最简单的模型是正态扩散模型。本文依据中国气象局雷电防护管理办公室发布的《全国雷电灾害汇编》和江苏省气象局统计的雷电灾害资料，从雷灾总数、伤亡人数、经济损失三个方面对2008—2019年江苏省的雷电灾害数据进行了整理、分析，提出了基于信息扩散理论的雷电灾害风险评估方法。

2 基于信息扩散理论的雷电灾害风险评估模型

假设X为雷电自然灾害指标，泛指广义的雷电灾害指标，T年内关于X的超越频率分布定义为雷电灾害风险。设X由一些具体的量值组成，记为

$ X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} $

(1)

又设损失超越X_i的雷电灾害风险概率为p_i，i = 1，2，…，n，其概率分布记为

$ P=\left\{p_{1}, p_{2}, \ldots, p_{n}\right\} $

(2)

如果区域过去m年内的某一雷电自然灾害指标实际记录分别为y₁，y₂，…，y_m，其观测样本集合记为

$ Y=\left\{y_{1}, y_{2}, \ldots, y_{m}\right\} $

(3)

y_j (j = 1，2，…，m) 均称为实际发生的某一雷电灾害样本。

假设实际发生的某一雷电灾害指数论域为

$ U=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\} $

(4)

一个单值观测样本y_j依式f_j(u_i)，可以将其所携带的信息扩散给u_i中的所有点。

$ f_{j}\left(u_{i}\right)=\frac{1}{h \sqrt{2 \pi}} \exp \left[-\frac{\left(y_{j}-u_{i}\right)^{2}}{2 h^{2}}\right] $

(5)

式中f_j(u_i) 表示实际发生的某一雷电灾害观测样本值y_j到点u_i上的信息量，u_i为信息吸收点，是雷电灾害论域内某个取值。h为扩散窗宽，即扩散系数，表示信息扩散的控制范围，其数值与样本容量有关，可根据雷电灾害样本集合中样本最大值b、最小值a和样本个数n来确定：

$ h=\left\{\begin{array}{ll} 0.8146(b-a), & n=5 ; \\ 0.5690(b-a), & n=6 \\ 0.4560(b-a), & n=7 ; \\ 0.3860(b-a), & n=8 ; \\ 0.3362(b-a), & n=9 \\ 0.2986(b-a), & n=10 ; \\ 2.6851(b-a) /(n-1), & n \geq 11 . \end{array}\right\} $

(6)

其中$ b=\max\limits _{1 \leq j \leq m}\left\{y_{j}\right\}, a=\min\limits _{1 \leq j \leq m}\left\{y_{j}\right\} $，令

$ C_{j}=\sum\limits_{i=1}^{n} f_{j}\left(u_{i}\right) $

(7)

相应的雷电灾害模糊子集的隶属函数为

$ \mu_{y_{j}}\left(u_{i}\right)=f_{j}\left(u_{i}\right) / C_{j} $

(8)

可以将μ_yj(u_i) 称为y_j的归一化信息分布。对所有样本均进行以上处理，并计算经信息扩散后推断出的雷电灾害指标值为样本个数。即为

$ q\left(u_{i}\right)=\sum\limits_{j=1}^{m} \mu_{y_{j}}\left(u_{i}\right) $

(9)

其物理意义是：由实际发生的某一雷电灾害样本{y₁，y₂，…，y_m}，经信息扩散推断出，如果雷电灾害数只能取{u₁，u₂，…，u_n} 中的一个的时候，在这种情况下，可以将y_j均看作是雷电灾害样本代表，观测值为u_i的样本个数为q(u_i)。显然，q(u_i) 通常不是一个正整数，但一定是一个不小于0的数。接着令

$ Q=\sum\limits_{i=1}^{n} q\left(u_{i}\right) $

(10)

事实上，Q可以被认为是各个雷电灾害论域u_i点上的样本数的综合。再令

$ P\left(u_{i}\right)=q\left(u_{i}\right) / Q $

(11)

上式中，P(u_i) 就是样本落在u_i处的概率值，可以作为概率的估计值。

对于雷电灾害要素指标X ={x₁，x₂，…，x_n}，通常将x_i取为论域U中的一个元素u_i。显然，超越u_i的概率应为

$ P\left(u \geq u_{i}\right)=\sum\limits_{k=i}^{n} P\left(u_{k}\right) $

(12)

式中P(u ≥u_i) 就是所要求的雷电灾害风险评估值。

3 江苏雷电灾害风险分析

江苏省处于东亚季风气候区，属亚热带和暖温带过渡气候，海岸线较长，受海洋气候影响明显。降水多集中于夏季的6月、7月之间，气象灾害种类繁多，尤其是雷电灾害，是中国遭受雷电灾害影响较严重的省份之一(林昕等，2008；郦嘉诚等，2012)。据不完全统计, 江苏省2008—2019年12 a间共发生雷电灾害3 720次，造成人员伤亡145人，经济损失高达7 248.07万元(QX/T103—2017)。从这些损失数字来看，对江苏省的雷电灾害风险进行评价分析非常必要。

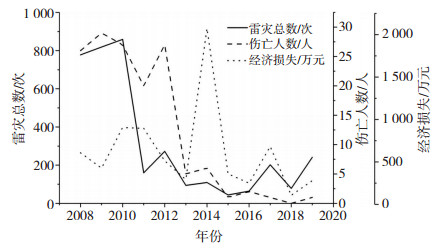
雷电灾害与人身生命安全及经济损失关系密切，统计江苏省2008—2019年的雷电灾害记录数据，提取雷灾总数、伤亡人数和经济损失因子，将数据拟合到图 1中。

由图 1可见，总体来看，2008—2019年间江苏省雷灾总数与雷击伤亡人数呈现波动下降的趋势。经济损失在2010—2019年间与雷灾总数变化也基本一致(除2014年比较异常外)。需指出的是，雷电发生时，常伴有大风、暴雨等自然灾害，其经济损失可能为多灾种致灾损失的总值。2014年经济损失相对过高(2 62.01万元)，这主要是由于2014年江苏省多地发生大风、暴雨及雷电的共生灾害，其灾害风险等级高于其它年份，造成经济损失在该年份达到峰值。2010— 2019年间的其它年份经济损失与雷灾总数变化基本一致。雷灾总数在2008—2010年间发生比较频繁，波动起伏不大，最多的达859次(出现在2010年)，之后雷灾次数变少。2015年雷灾出现次数较少，仅为44次。伤亡人数2008—2012年间每年大约20多人次，此后逐渐减少，2013—2019年间每年在10人以下。2018年由雷电所引起的经济损失为最低值(93.95万元)。整体分析来看，经济发展、信息化水平提升与社会防灾减灾能力不足之间的矛盾，会造成雷灾总数及相应损失的增加。随着雷电防护科学知识的深入普及、公众防灾减灾意识的增强及防雷设施的不断完善，江苏省的雷灾总数、伤亡人数及相应损失呈现下降的趋势，特别是最近几年雷击伤亡的人数均维持在3人以下，从一个侧面表明了近些年江苏省雷电灾害防御工作开展的有效性。

依据信息扩散原理对上述三组数据进行分析，建立江苏省雷电灾害风险评估模型，对各个风险因子做出评价判断。根据2008—2019年江苏省雷电灾害总数的变化范围[44, 859], 将一维实数空间上的集合[40, 880]作为x_1i的论域，将连续论域按等间距40取点，转变为离散论域。考虑到计算精度的要求，取22个控制点(n₁ = 22)，构成离散论域

$ U_{1}=\left\{u_{11}, u_{12}, \ldots \ldots u_{122}\right\}=\{40, 80, \ldots \ldots .880\} $

(13)

根据2008—2019年江苏省雷电灾害伤亡人数变化范围[0, 29]，将一维实数空间上的集合[0, 30]作为x_2i的论域，将连续论域按等间距3取点，转变为离散论域。考虑到计算精度的要求，取11个控制点(n₂ = 11)，构成离散论域

$ U_{2}=\left\{u_{21}, u_{22}, \ldots \ldots u_{211}\right\}=\{0, 3, \ldots \ldots 30\} $

(14)

根据2008—2019年江苏省雷电灾害经济损失变化范围[93.95, 2 062.01]，将一维实数空间上的集合[50, 2 250] 作为x_3i的论域，将连续论域按等间距200取点，转变为离散论域。考虑到计算精度的要求，取12个控制点(n₃ = 12)，构成离散论域

$ U_{3}=\left\{u_{31}, u_{32}, \ldots \ldots . u_{312}\right\}=\{50, 250, \ldots \ldots .2250\} $

(15)

用Matlab软件编程，实现公式(4)—(15)的计算过程，得到雷电灾害次数、人身伤亡数和经济损失的风险估计值。

由表 1可以看出，雷灾风险水平随着雷灾次数的增多，其发生概率减小，风险水平主要集中在320次·a^-1以内，大约每1.9 a遇到一次，而发生880次·a^-1以上的概率较小，大约38.2 a遇到一次。人员伤亡事件多发生于农村正从事劳作的人员身上，人员伤亡风险水平主要集中在12人·a^-1内，大约每1.8 a遇到一次，大于30人·a^-1的概率较小，约14.1 a遇到一次(表 2)。经济风险水平值则较高，风险值为650万元·a^-1的累积发生概率高达58.62%，2 250万元·a^-1的发生概率极小，约54.4 a一次(表 3)。

4 结论与讨论

本文利用信息扩散原理，通过分析江苏省2008— 2019年的雷电灾害数据记录，对其雷电灾害风险进行了定量化分析，结果显示：江苏省雷电灾害事故次数多集中在320次·a^-1以内，人员伤亡风险水平主要分布在12人·a^-1以内，经济风险水平主要集中在650万元·a^-1之内，均2 a内可遇到一次。总体来看，2008— 2019年间江苏省雷灾总数、雷击伤亡人数以及经济损失呈现波动下降的趋势，江苏省近些年雷电灾害防御工作持续有效的开展，雷电防护科学知识的深入普及，是雷电灾害事故次数、伤亡人数及经济损失减少的主要推动因素。

应用信息扩散理论进行雷电灾害风险评价，可对防灾减灾提供一定的参考作用，并为相关政府部门防灾减灾决策提供科学的参考依据。但是，其最终的计算结果只表明一种平均情况，评价结论存在一定的局限性，因此需对其评价结果有正确的认识。在后续的研究中还将尝试考虑其它的气象因子进行综合研究，使分析结果更全面、更综合。