引言

随着观测技术的进步和资料同化方法的不断精细化发展，以及计算机和预报技术的革新，天气和气候预测水平在过去的几十年间得到了极大的提高(Anderson, 2001; Hunt et al., 2004; Ott et al., 2004; Whitaker and Hamill, 2002; 陈德辉等，2004)。然而，即使初始场越来越精确，仍不可能与真实大气完全一致，并且由于动力框架的不完善和参数化方案的不足，没有一个模式的的演变机制和真实大气完全吻合，这些方案的每一步改进都需要理论创新的支持，因此，对初始场和模式进行改善是改进数值预报的必要条件(钟剑等，2011)，但并非充分条件。

除了对初始场和模式进行直接改善外，现有的大量历史资料和统计学方法为预报误差订正提供了新的思路。不少学者提出在给定的初始数据和数值模式的前提下，利用历史资料修正模式误差(Derber, 1989；Zupanski et al., 2006；顾震潮，1958；邱崇践等，1989)。Danforth等(2007)提出将模式误差分为状态独立项(又名偏差bias，常数，为长时间的预报误差的平均)，状态依赖项(依赖于某些状态变量)和随机误差(噪音)，并比较了在线订正和线下订正两种经验订正方法对偏差的订正效果。线下订正直接将误差统计关系应用到模式输出场以提供给用户更好的预报结果，优点在于比较简单，但不能适时更新。而在线订正是在模式的每一步积分过程中都对模式误差起作用，这会对模式动力产生影响。结果表明，在线订正有更小的均方根误差和更大的距平相关，并且减小了偏差的非线性增长，即减小了模式误差的累积效应，它的不利因素在于如果增加到模式强迫的估计残差大，可能会干扰模式变量的物理平衡。丑纪范(1986)提出了动力——统计相结合的思路，将观测看作大气模式的足够精确的解，通过解反问题的方式来修正模式误差，并得到了进一步的发展(黄建平等，1991; 苏海晶等，2015)。

一些学者将模式预报误差分为系统误差和非系统误差两部分(万仕全等，2014)，其中系统误差为模式预报误差的多年平均，将系统误差从预报误差中扣除后的余下部分为非系统性误差，非系统性误差是随时间和大气状态变化的，又可分为状态依赖误差和随机误差两个部分。系统性误差订正的订正量不依赖于模式变量，常用的方法是计算大量预报误差的平均值(考虑季节变化和日变化)，将其叠加到对应预报时效的当前输出结果上。系统误差订正多用于气候模式误差的订正(高峰等，2016)。如曾庆存等(1990)在短期气候预测中将预报场的气候平均用实况的气候平均代替，将预报场的距平叠加到实况的气候平均上作为预测值，从而去除模式的气候漂移项；Peng等(2013)提出一种新的距平集合方法，通过利用历史分析资料确定变量场的真实气候平均和预报气候平均，以两者的差值作为模式偏差订正项对预报进行订正，剔除模式误差，从而实施15 d的确定性的数值天气预报。对于非系统性误差的订正，因其具有的状态依赖的特点，订正难度较大。Ferranti等(2002)在分析90年代北大西洋涛动变化和ECMWF 500 hPa高度场预报误差间的关系时发现，误差的状态依赖成分占到总的误差方差的10%。Leith(1978)提出用经验统计的方法来估计状态依赖的模式误差，其中模式倾向误差被视为是状态变量的线性函数，它的统计模式可以由预报状态的时间序列得到。Delsole等(1999)用一个非线性准地转模式测试了简化的Leith方案，发现状态依赖的订正方法确实提高了模式的预报技巧。Zupanski等(2006)在其提出的对模式误差估计的新方法中结合了集合资料同化方法、状态增广方法和模式与偏差估计方法，并对其效果进行了检验。这些方法对预报误差的订正都有一定的效果，Danforth等(2008)指出如果模式状态变量的自由度是N，那么Leith方法在每一个时间步长里都需要N³个浮点运算，很显然这样的运算量过大。因此，Danforth提出SVD技术来对Leith的计算方法进行降维处理，如此一来，改善了这一方法在实际应用中的可行性。邵爱梅等(2009)在寻找与非系统性预报误差相关的预报场或预报场组合的尝试中，利用浅水方程模式，采用三种预报场组合方案进行理想试验，这三种组合方案分别为预报结束时刻预报场，初始场和结束时刻预报场，结束时刻预报场和预报倾向场。并在Danforth等的基础上(运用SVD)，进一步采用变分法通过极小化来求解，使解有更好的稳定性，也容易加入其它约束条件(比如背景项)。结果表明，采用结束时刻预报场和预报倾向场这一组合进行预报误差订正的效果最好。此外，神经网络(陈德花等，2010；李虎超等，2015；殷志远等，2013)的方法也被用来进行求解。

根据相似理论，相似的状态变量可能导致相似的预报误差(丑纪范等，2006；任宏利等，2005)，因此可以利用历史资料建立状态变量与非系统性预报误差间的映射关系时，从历史资料中选择与分析时刻的预报样本相似的样本集合作为训练样本来建立非系统性误差与状态变量间的映射关系，期望能更有效地对预报做出订正(王启光等，2011)。目前在大气科学领域常用的相似性度量有海明距离、欧氏距离、相关系数、相似系数、相似离度(Huang et al., 1993)等。相似面积比方法是一种证实有效的选择相似样本的方法(何邓新等，2014)。在相似样本的选择中着重于从全局的角度尽可能多的寻找样本的相似点，避免了现有方法中受少数因子影响的缺陷。判断相似的阈值在一定程度上反映了值差异的程度，而相似面积大小则能部分反映出形相似的程度。对数据的标准化处理则有利于综合值域、量纲、量级都不相同的多个气象要素场来建立综合性的相似判据。

变分方法可以有效建立预报误差和预报场组合之间的映射关系，奇异值分解技术可以减小维度使这一方法得以较便利地实现，但尚未在复杂模式中进行检验，因此，本文首先将邵爱梅等(2009)提出的方法应用于GRAPES模式，研究该方法在复杂模式中对预报误差的订正效果。然后利用相似面积比方法从历史样本集合中选取与检验样本分析场相似的样本构成样本集，以此相似样本集作为训练样本，利用变分方法来建立状态变量和非系统误差之间的映射关系，对非系统性预报误差做出估计，并评估这两种方法对预报的订正效果。

1 试验方法简介 1.1 试验区域及预报误差样本

本文使用的资料包括：(1) GRAPES模式(版本: GRAPES_Meso3.0) 2002—2010年全球回报资料，其中模式初始场由NCEP 1日4次FNL 1°×1°分析资料产生，模式模拟分辨率为1°×1°；(2) 2002—2010年的NCEP— FNL资料，已预先处理到GRAPES模式格点上。

在本文的数值试验中，试验区域是东亚地区(70°—140°E, 10°—60°N)，试验数据选用2002—2010年6—8月GRAPES模式500 hPa 48 h高度预报场回报资料，相应时刻的NCEP—FNL分析资料视为“真实场”。预报误差e为FNL分析场x^t和同一时刻的GRAPES预报场x之差，即

$ e = {x^t} - x $

(1)

对2002—2010年预报误差e求平均值得到系统误差场e，将系统性误差从预报误差中扣除后，余下部分即为非系统性误差e'，即

$ {e^\prime } = e - \bar e $

(2)

由此得到2002—2010年6—8月GRAPES模式500 hPa高度场48 h预报的非系统性误差样本共828个。分别选取2008、2009和2010年7月GRAPES模式500 hPa高度场48 h预报的31个非系统误差样本作为检验样本，以2002—2010年中除检验样本外的其余年份7月的248个样本集合作为训练样本进行预报误差订正试验，该方法简称DEM方法。用从其余年份6—8月的样本中筛选的240个相似样本集作为训练样本进行同样的误差订正试验，该方案记为SEM方法，以检验相似样本集能否进一步提高预报订正效果。以NCEP— FNL资料作为真实大气对预报误差订正效果进行检验。

1.2 相似样本集的建立

利用2002—2010年6—8月GRAPES 500 hPa高度预报场和对应时刻的FNL资料，应用公式(1)和(2)得到非系统性预报误差时间序列，共计828个样本。相似样本集的具体获取方法如下：若取某一年(如2008年)7月的非系统预报误差场作为检验样本集，则其他非系统误差样本作为历史样本集合。对于任一检验样本，利用相似面积比方法从上述历史样本集合中选取分析场与该检验样本分析场最相似的前240个样本构成相似样本集。以此相似样本集作为训练样本。

相似面积比方法的具体算法(何邓新等，2014)如下：

首先对分析场序列X (λ, φ, t)按下式进行标准化处理，使其具有无量纲性质

$ \hat X(\lambda ,\phi ,t) = \frac{{X(\lambda ,\phi ,t) - \bar X(\lambda ,\phi )}}{{\sigma (\lambda ,\phi )}} $

(3)

其中：X (λ, φ)为分析场序列的多年平均值；σ(λ, φ)为标准差；λ, φ, t分别为经度、纬度和时间。

建立相似判据。计算样本集$\widehat X$ (λ, φ, t)中两两样本场$\widehat X$ (λ, φ, t_i)与$\widehat X$ (λ, φ, t_j)之差的绝对值，即

$ \Delta ({t_i},{t_j}) = \sum\limits_{\lambda = 1}^L {\sum\limits_{\phi = 1}^M {{w_\phi }} } |\hat X(\lambda ,\phi ,{t_i}) - \hat X(\lambda ,\phi ,{t_j})|/\sum\limits_{\lambda = 1}^L {\sum\limits_{\phi = 1}^M {{w_\phi }} } $

(4)

其中：w_φ = cos φ，L和M分别为$\widehat X$ (λ, φ, t_i)在经度和纬度方向的格点数。加入这个权重是考虑到在经、纬度坐标中不同纬度格点代表的面积随纬度变化。计算所有的Δ(t_i, t_j)的平均值得到$\overline \Delta $，将$\overline \Delta $/2作为判断相似的阈值C。对于给定基准样本$\widehat X$ (λ, φ, t_B)和任意历史样本$\widehat X$ (λ, φ, t_H)定义新的相似性度量——相似面积比(Re)为

$ {\mathit{Re}} ({t_B},{t_H}) = \frac{{{{\left. {\sum\limits_{\phi = 1}^M {\sum\limits_{\lambda = 1}^L {{w_\phi }} } } \right|}_{d(\lambda ,\phi ) < C}}}}{{\sum\limits_{\phi = 1}^M {\sum\limits_{\lambda = 1}^L {{w_\phi }} } }} $

(5)

其中：d(λ, φ) =|$\widehat X$ (λ, φ, t_B) - $\widehat X$ (λ, φ, t_H)|。即通过判断两样本之差值场中绝对值小于阈值的面积与总面积的比值的大小来判定样本的相似程度，比值越大就说明样本越相似。如果数据格点按面积是均匀分布(w_φ = 1)，(5)式计算的就是小于阈值的点数与总格点数的比值。

1.3 变分方法

假设非系统性误差e'_k与末时刻预报场和预报倾向场组成的预报场组合$f_{k}\left(x^{\prime}\right)=\left(x^{\prime}\left(t_{k}+\tau\right)^{T}, \left[x^{\prime}\left(t_{k}+\tau\right)-x^{\prime}\left(t_{k}\right)\right]^{T}\right)^{T}$间存在着映射关系H

$ {f_k}({x^\prime }) = {\rm{H}}e_k^\prime $

(6)

e'_k和f_k(x')可以表示为按照一组P阶正交向量展开的形式，即

$ {e_k^\prime = \sum\limits_{i = 1}^p {{\alpha _i}} b_i^e = {b^e}\alpha } $

(7)

$ {{f_k}({x^\prime }) = \sum\limits_{i = 1}^P {{\alpha _i}} b_i^f = {b^f}\alpha } $

(8)

其中α是由展开系数组成的矢量，正交基向量b = ((b^e)^T, (b^f)^T)^T是从训练样本的非系统性误差和预报场组合组成的集合中通过奇异值分解得到的，b^e和b^f分别对应于非系统性误差和预报场组合的部分。正交基向量的计算过程具体如下：首先得到M个训练样本非系统性误差eⁱ' (i=1, 2, …, M)及预报场组合f_i(x') (i=1, 2, …, M)。由非系统性误差和预报场组合耦合得到列向量${a_i} = {\left({e_i^T, f(x')_i^T} \right)^T}$，将这些列向量a_i组合可以得到M个列向量的矩阵A。对A作奇异值分解并将A的特征值按照从大到小的顺序排列，A的左特征向量B中前P个非零特征值对应的b_i即为式(7)和(8)中计算所需要的奇异向量。估计非系统性预报误差的问题可表示为极小化以下目标函数的形式

$ J(e_k^\prime ) = e_k^T{\mathit{\boldsymbol{P}}^{ - 1}}e_k^\prime + {[{f_k}(x) - He_k^\prime ]^T}{\mathit{\boldsymbol{O}}^{ - 1}}[{f_k}(x) - He_k^\prime ] $

(9)

其中P是背景误差协方差矩阵，O是观测误差协方差矩阵。应用公式(7)和(8)，目标函数(9)可表示为：

$ J(\alpha ) = (M - 1){\alpha ^T}\Lambda _P^{ - 2}\alpha + {({f_k}(x) - {b^f}\alpha )^T}{\mathit{\boldsymbol{O}}^{ - 1}}({f_k}(x) - {b^f}\alpha ) $

(10)

其中P≈ b^e ∧_P²(b^e)^T /(M - 1)，通过极小化上述目标函数求得系数α，再由式(7)求得非系统性误差e'_k。

2 预报误差特征分析 2.1 系统性误差空间特征分析

为了解GRAPES模式的预报能力，首先计算2002—2010年东亚地区7月的500 hPa高度场48 h预报的系统性误差场。图 1给出了GRAPES模式7月份东亚地区500 hPa高度场48 h预报的系统性误差场，可以看出，高度场的系统性误差呈现出自南向北由正值减小至负值的趋势，说明在低纬度地区GRAPES的预报值偏低，高纬度GRAPES模式的预报值偏高，尤其是在青藏高原地区，48 h系统预报偏差最大值为28 gpm。这反映了GRAPES模式对大尺度地形地区的动力热力过程描写可能存在缺陷。

2.2 非系统性误差特征分析

上文分析了系统性误差空间分布特征，现对非系统性误差的空间分布特征进行初步分析，并估算非系统性误差在预报误差中比重。

从随机给出的若干样本的非系统性误差场可以看出相同预报时效下的非系统性误差的量级与系统性误差基本相当。本节分别利用2008—2010年7月48 h预报误差样本，对非系统性误差在预报误差的占比情况进行逐年估算。以2008年7月31个48 h预报误差样本为例，具体计算方法如下：首先对样本k中第i个格点，非系统性误差占该格点预报误差的比重r_{i, k}为

$ {r_{i,k}} = \left| {\frac{{e_{i,k}^\prime }}{{{e_{i,k}}}}} \right| = \left| {\frac{{e_{i,k}^\prime }}{{\overline {{e_{i,k}}} + e_{i,k}^\prime }}} \right| $

(11)

其中e_{i, k}为预报误差，e'_{i, k}为非系统性误差。当e'_{i, k} =0时，r_{i, k} =|e'_{i, k} /e_{i, k}|= 0。考虑到e_{i, k}为零的情况下计算无意义，这时r_{i, k}用下式计算：

$ {r_{i,k}} = \left| {\frac{{e_{i,k}^\prime }}{{\overline {{e_{i,k}}} + e_{i,k}^\prime }}} \right| \ge \frac{1}{{\left| {\frac{{\overline {{e_{i,k}}} }}{{e_{i,k}^\prime }}} \right| + 1}} $

(12)

对31个样本(n_t)所有格点(n_x)的r_{i, k}求平均值，即得到2008年7月48 h非系统性误差的比重r：

$ r = \frac{1}{{{n_x}{n_t}}}\sum\limits_{k = 1}^{k = {n_t}} {\sum\limits_{I = 1}^{i = {n_x}} {{r_{i,k}}} } $

(13)

从式(13)可以看出，我们计算得到的r实际上是非系统预报误差占预报误差比例的下限。

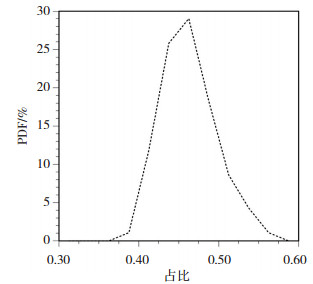
图 2给出2002—2010年7月东亚地区500 hPa高度场48 h非系统性误差在预报误差中所占比重的概率分布函数（PDF），可以看出非系统性误差占比在40%~55%左右，平均值为45%，反映出对非系统误差订正的重要性和必要性。

3 结果分析 3.1 变分方法中截断阶数的敏感性试验

从公式(7)可以看出，非系统性误差表示成SVD基底的展开形式，α截断阶数的选取是影响该方法估算非系统预报误差效果的重要因素。因此在进行非系统性误差估计之前，我们首先进行截断阶数的敏感性试验来确定后面分析所使用的截断阶数。

分别以2008、2009、2010年7月500 hPa高度场48 h预报误差作为检验样本，利用变分方法建立非系统性预报误差与训练样本预报场组合间的映射关系，从而估计检验样本的非系统性误差，在对检验样本进行系统性误差订正的基础上，对预报进行非系统性误差订正。在10—70范围内每隔5个截断阶数进行一次敏感性试验，变分方法估算非系统性误差的能力通过分析预报订正的效果来评估。具体评估方法如下：对第k个检验样本的预报x_k进行系统性误差订正得到，将变分方法估算得到的非系统性预报误差进一步叠加在系统性误差订正的预报上，得到最后的订正预报场x_k^s = x_k^c + e^s，计算与该样本对应的分析场x_k^t之间的均方根误差(RMSE)：

$ RMSE_k^s = \sqrt {\frac{1}{{{n_x}}}\sum\limits_{i = 1}^{i = {n_x}} {{{(x_{k,i}^s - x_{k,i}^t)}^2}} } $

(14)

其中n_x为预报场的格点总数，x_{k, i}^s和x_{k, i}^t分别为订正后预报和分析场的第i个格点的变量值，均方根误差越小，订正后预报与真实值越接近，订正效果越好。订正预报结果表明变分方法中截断阶数取10—70时，预报均方根误差的平均值较小。表 1给出了截断阶数取10到40时2008—2010年31个检验样本经非系统预报误差订正后的预报均方根误差的平均值。从表 1可以看出，对于DEM方法，截断阶数为15时，预报均方根误差的平均值最小，对预报的订正效果最优。而对于SEM方法，截断阶数为35时订正预报的效果最优。因此，以下分别选取截断阶数为15时DEM方法的试验结果和截断阶数为35时SEM方法的试验结果对非系统误差估计场的空间分布特征和预报订正结果进行具体分析。

3.2 非系统性误差估测效果

图 3随机给出2009年7月23日、2008年7月17日和2010年7月19日这三个样本DEM和SEM两种方法得到的48 h非系统性误差场及模式非系统性误差。从图中可以看出，针对2009年7月23日这一个例(b, e, h)，两种方法对非系统性预报误差都有一定的估算能力，估算的非系统性误差场和模式非系统性误差场的空间分布特征较为一致，但相比而言，SEM方法估算的非系统误差场与模式非系统性误差更为接近，比如在新疆及其附近区域，SEM方法估算的非系统误差场与模式非系统性误差场有较好的对应关系。从误差场的数值上来看，两种方法得到的非系统误差都低于模式非系统性误差。经系统性误差订正后预报的均方根误差由16.398 gpm降至13.361 gpm，经SEM和DEM估算的非系统误差进一步订正后预报的均方根误差分别为11.219 gpm和11.349 gpm，针对这一个例，SEM方法估算非系统误差的能力略好于DEM方法。

2008年7月17日(c, f, i)这一个例，SEM和DEM两种方法得到非系统误差估计值较一致。在45°N以北区域，SEM估计的非系统误差空间分布形态和模式非系统性误差场较为一致，但估计值偏小。在山西附近，模式非系统性误差场和DEM方法得到的估计值均为负值区，而SEM得到的结果为正值区，SEM方法估计效果较差。从预报订正效果看，经系统性误差订正后的预报均方根误差由11.927 gpm减为8.644 gpm，经SEM和DEM估算的非系统误差进一步订正后预报的均方根误差分别为8.562 gpm和7.996 gpm，说明两种方法估算的非系统误差都能对预报做出进一步有效订正，但DEM方法得到的结果优于SEM方法。

2010年7月19日(c, f, i)是一个非系统误差估计失败的个例。从图中可以看出，除了东北地区的非系统性预报误差的估计场和模式非系统性误差场空间分布较为一致，两种方法在青海和新疆等地的估计值都有很大偏差，这种大范围的对非系统性误差的错误估计会导致非系统误差的订正起到负面作用，预报订正结果也证明了这一点。经SEM和DEM估算的非系统性误差订正后的预报均方根误差分别为12.637 gpm和12.154 gpm，相对于系统订正后的预报均方根误差11.364 gpm均有所增大。这可能是样本库数目的局限造成的，可能在扩大样本库之后得到解决。此外，由于选取相似样本时，考虑到在经纬度坐标中不同纬度格点代表的面积随纬度变化，对不同纬度面积计算增加了一个权重，低纬度权重较大，高纬度权重较小，而在进行误差订正结果评估时，没有考虑到地图的变形，这可能是造成相似样本订正效果没有明显优势的原因。

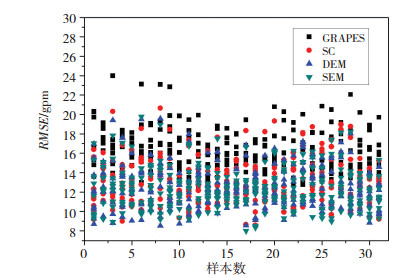
3.3 预报误差订正效果分析

将非系统性误差的订正效果进行分析，并和系统偏差订正的结果作比较。图 4为2002—2010年7月各个检验样本的48 h 500 hPa高度场预报的GRAPES模式、经系统性误差订正后、DEM和SEM方法非系统性误差订正后的预报均方根误差。对于279个检验样本，500 hPa的48 h高度预报场经系统性误差订正后，268个样本的预报均方根误差明显降低，预报订正效果明显。SEM和DEM两种方法得到的非系统性误差订正能进一步修正预报结果，相对系统误差订正而言，有176个样本经DEM方法订正后预报效果进一步提高。SEM方法在系统误差的基础上对预报作出进一步有效订正的样本共182个。可以看出，系统性误差订正的效果是比较明显的，而对于非系统性误差订正，在系统性误差订正的基础上，对预报的改进效果较不明显，下面将以定量分析来评估订正效果。

GRAPES模式2002—2010年的检验样本在订正前，预报均方根误差平均值为16.069 gpm，经系统订正后下降为13.017 gpm，经DEM和SEM得到的非系统性误差进一步订正后分别为12.474 gpm和12.392 gpm。对总体而言，两种方法都能在系统误差订正的基础上进一步对预报作出有效订正，并且SEM方法的订正效果好于DEM方法。采用配对t检验对订正前后的预报均方根误差进行显著性检验，发现不论是DEM还是SEM方法估计的非系统性误差对预报进行订正后，预报均方根误差都和只进行系统性误差订正的预报均方根误差间有显著差异，这说明这两种方法对预报的订正与只进行系统性误差订正是有明显差异的，订正是有意义的。对DEM和SEM方法订正后的预报均方根误差进行配对t检验，发现并未通过显著性检验，说明两者之间的差异不大，因此SEM方法订正后的预报均方根误差的平均值虽然小于DEM方法，但两者间差异并不显著，采用相似样本作为训练样本对预报误差的订正相较于DEM方法并没有明显改善。

为了进一步了解非系统性误差订正的效果，计算每个检验样本误差订正后预报均方根误差与订正前GRAPES预报均方根误差的比值

$ p_k^c = \frac{{RMSE_k^c}}{{RMSE_k^f}} $

(15)

并统计279个样本比值分布情况，如果比值小于1，则说明系统性误差对预报的订正有效，比值越小，订正效果越好；如果比值大于1，则说明订正无效。

表 2为2002—2010年7月共279个检验样本经系统误差订正和SEM、DEM两种方法估计的非系统性误差对预报进一步订正后的均方根误差与GRAPES模式预报的均方根误差比值的统计结果。如表中所示，经过系统性误差订正后，279个样本中有268个样本的订正是有效的，其中有39个样本的订正效果明显(比值小于0.7)。应用DEM和SEM方法对预报进一步订正后，预报得到明显改善的样本数分别为55和65(比值小于0.7)，经过系统和非系统两步订正后，预报订正有效率分别达到96.057%和100%。相对系统误差订正而言，SEM方法订正效果改善效果并不明显。

4 结论与讨论

预报误差包含反映气候特征的系统性误差部分和反映天气状态的非系统性误差部分，基于非系统性误差状态依赖的特点，以2002—2010年7月500 hPa高度场48 h预报作为检验样本，分别以相似面积比方法筛选的相似样本集合和相同时刻历史样本作为训练样本，建立预报场组合与非系统性误差间的映射关系，从而估计非系统性误差，并在对预报进行系统性误差订正的基础上，进行进一步非系统性误差订正。试验结果表明：

(1) DEM方法和SEM方法估计的非系统性误差空间分布的正负区域与模式非系统性误差的对应较好，估计值的量级也与模式非系统性误差相一致，数值偏小。与DEM方法相比较，SEM方法表现出微弱优势。

(2) 对279个检验样本的试验结果表明，SEM方法和DEM方法都对非系统性误差有一定的估算能力。经过系统性误差和非系统性误差两步订正后，DEM方法和SEM方法的订正有效率分别为98.566%和100%。两者之间的差异并未通过配对t检验，两种方法的优劣区分较不明显。

需要注意的是，由于我们将分析场当做真实场来对待，分析误差会对预报误差的修正产生一定的影响；随着模式的更新，训练样本与订正时刻样本的误差产生机制会出现差异，尤其是系统性误差，这就需要不断更新训练样本；本文中选择相似样本进行误差估计的优势并不明显，随着训练样本数量的积累，在相似的基础上选择训练样本的优势可能会更加凸显出来。

在本文中，DEM方法和SEM方法仅被应用于GRAPES 500 hPa高度场，为利用历史数据订正数值模式的预报误差提供了一个新的思路，该方法在其他模式和其他变量以及多变量多高度层中的应用值得进一步研究。