引言

暴雨、短时强降水是我国暖季最主要的灾害性天气，两者既有联系又有明显区别，不可混为一谈。日常天气预报和诊断研究过程中，所遵循的预报物理基础和技术方法本应存在显著不同。短时强降水(flash heavy rain)是指在短时间内出现的很强的降水事件，我国天气预报业务中一般指1 h雨量在20 mm或3 h雨量在50 mm以上的降水事件；暴雨是指24 h内累计降水量达到或超过50 mm的天气事件^[1]。在时间尺度上，前者强调降水强度，即雨强；后者侧重描述天气过程造成的累计降水，即雨量。在空间尺度上，短时强降水一般由对流降水形成，且为典型的中小尺度系统驱动，其造成的衍生灾害往往表现为局地而短促，如山体崩塌、滑坡、城市道路积水、暴洪(flash flood)；而大范围暴雨更多是指更大尺度天气系统主导下的大范围持续性降水，更易形成区域性洪涝灾害，当然，局地性暴雨过程往往和短时强降水有密切联系。从其相互关系看，一次短时强降水事件不一定形成暴雨，如由移动性雷暴系统形成的短时强降水，最大雨强可达到3 mm·min^-1(或180 mm·h^-1)，雷暴通过某一地点形成的强降水事件如果只持续了10 min，累计降水量只能达到大雨量级，但持续性或间歇性的短时强降水必然形成暴雨甚至特大暴雨事件^[2-4]；一次暴雨事件不一定包含短时强降水，如以层状云降水为主、雨强仅为5 mm·h^-1左右的持续性降水，其24 h降水量即可达到大暴雨量级，极端性层云降水甚至可形成特大暴雨。不过，我国暖季暴雨过程中，大暴雨或特大暴雨天气过程中往往存在中尺度对流性短时强降水过程。

在实际预报业务和天气机理研究过程中，有人将暴雨和短时强降水混为一谈，或将暴雨预报分析方法错误地直接用于短时强降水预报分析。针对这种现象，本文从水汽方程的尺度分析入手，讨论不同尺度、不同性质的降水过程中降水强度的动力学主导因子，强调暴雨和短时强降水预报分析中应关注其区别和联系，以期为相关专业人员开展诊断研究和降水预报提供基本思路。

1 不同尺度天气系统降水强度估算的物理基础

单位时间内大气柱中绝对水汽含量的净减少值即为雨强，即

$ R=\int_{{{p}_{0}}}^{p}{-\frac{\text{d}\mathit{q}}{\text{d}\mathit{t}}\text{d}\mathit{p}} $

(1)

其中，R为单位面积上的降水强度。对应z坐标的水汽方程为

$ \frac{\text{d}\mathit{q}}{\text{d}\mathit{t}}=\frac{\partial \mathit{q}}{\partial \mathit{t}}+\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}+w\frac{\partial \mathit{q}}{\partial \mathit{z}} $

(2)

其中：$\frac{\partial \mathit{q}}{\partial \mathit{t}} $为气柱内水汽的局地变化项，取决于气柱内单位时间内蒸发、凝华、凝结和耗散等物理过程；$\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}$为气柱内水汽的净平流量；$w\frac{\partial \mathit{q}}{\partial \mathit{z}}$为水汽垂直输送量。为了简化问题，以下讨论只分析宏观动力学过程对降水效率的影响。

就天气尺度系统而言，$\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}$的量级为10¹·10¹·10^-6(即10^-4); $w\frac{\partial \mathit{q}}{\partial \mathit{z}}$的量级为10^-2·10¹·10^-4 (即10^-5)。

对于典型非对流性中尺度降水，$\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}$的量级为10¹·10¹·10^-5 (即10^-3)，$w\frac{\partial \mathit{q}}{\partial \mathit{z}}$的最大量级为10⁰·10¹·10^-4 (即10^-3)。

对中尺度对流系统而言，$\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}$的量级依然为10¹·10¹·10^-5 (即10^-3)。由于对流系统内的垂直速度主要源于对流有效位能(CAPE)的释放，即理论最大垂直速度$ w=\sqrt{2CAPE}$为10¹~10² m·s^-1量级，因此，$ w\frac{\partial \mathit{q}}{\partial \mathit{z}}$的最大量级为10²·10¹·10^-4(即10^-1)。

如果不考虑气柱中水汽含量的局地变化，对天气尺度系统来说，水汽垂直输送量比气柱内水汽的净平流量小一个量级，降水强度主要由水汽净平流量决定。

对于中尺度天气系统而言，如果是非对流性的层云降水过程，水汽垂直输送量和气柱内水汽的净平流量是一个量级，对应的降水强度约为每小时几毫米(10⁰ mm·h^-1)；对于对流系统而言，最大水汽垂直输送量比气柱内水汽的净平流量大两个量级，降水强度主要由后者决定，降水强度最大可达到每小时百毫米量级(10¹~10² mm·h^-1)。由此看到，由水汽方程推导得到的不同性质降水过程的降水强度与日常观测得到的降水强度是一致的，这也解释了大范围暴雨过程中为什么尽管降水持续时间差异很小但降水量分布特别不均匀的原因，即由天气尺度主导的降水过程在一定区域内相对均匀，如果其中存在若干中尺度非对流性过程(层状云降水过程，如层结稳定背景下的地形强迫、中尺度锋区、辐合线等)，可能出现若干暴雨中心，其降水量比区域平均降水量大一个量级；如果存在明显对流过程，降水区内的降水强度可能相差数十甚至近百倍，因而造成降水分布的极端不连续。

公式(2)中，$\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}=\nabla \cdot \left( q\vec{v} \right)-q\frac{\partial \vec{v}}{\partial \mathit{\vec{s}}}$，并结合质量方程$\frac{\partial \vec{v}}{\partial \mathit{\vec{s}}}+\frac{\partial \mathit{w}}{\partial \mathit{z}}=0$，式(2)可写为

$ \frac{\text{d}\mathit{q}}{\text{d}\mathit{t}}=\frac{\partial \mathit{q}}{\partial \mathit{t}}+\vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}}+w\frac{\partial \mathit{q}}{\partial \mathit{z}}=\frac{\partial \mathit{q}}{\partial \mathit{t}}+\nabla \cdot \left( q\vec{v} \right)+\frac{\partial q\mathit{w}}{\partial \mathit{z}} $

(3)

对于天气尺度，$\nabla \cdot \left( q\vec{v} \right)$量级为10^-4，$\frac{\partial q\mathit{w}}{\partial \mathit{z}}$量级为10^-5。因此，天气尺度的降水强度理论上主要取决于整个气柱的水汽通量水平辐合(即水汽通量散度的垂直积分)。

对于中尺度对流系统而言，$\nabla \cdot \left( q\vec{v} \right)$比$\frac{\partial q\mathit{w}}{\partial \mathit{z}}$小1~ 2个量级。由于对流系统中同时存在强烈的蒸发过程(这一过程是地面冷池和雷暴大风强度的重要驱动因子)。因此，地面有效对流降水强度可近似写为

$ {{R}_{c}}=E\int_{{{z}_{0}}}^{z}{\frac{\partial q\mathit{w}}{\partial \mathit{z}}}\text{d}\mathit{z=E}\left( \int_{{{z}_{0}}}^{z}{q\frac{\partial \mathit{w}}{\partial \mathit{z}}}\text{d}\mathit{z}+\int_{{{z}_{0}}}^{z}{w\frac{\partial q}{\partial \mathit{z}}}\text{d}\mathit{z} \right)\approx Eqw $

(4)

其中E为对流系统的实际有效凝结率。

对于对流系统而言，云中最大垂直速度位于平衡高度(EL)，也即云中的上升速度是随着高度增加而加大的，而水汽垂直分布是随着高度迅速减小的，多数情况下最大上升速度位于对流层上部，而该高度上大气绝对含水量很小(q≈0)；地面比湿最大，但是垂直速度为0。因此，相对而言，如果对流有效位能主要位于对流层中下层(表明对流上升运动的中心位置越低)，即与最大水汽含量层越接近，降水强度就越大。或者说，对流降水强度在很大程度上取决于云底的水汽垂直输送强度。

2 暴雨和短时强降水分析预报的关键因子

只有理解了第1节大气运动过程中降水形成的主要控制因素，才能对不同尺度、不同性质的天气过程中降水预报分析的关键点有一个较为清晰的认识。然而，在实际天气分析和诊断研究过程中，往往存在一些看似合理的分析方法却可能在物理逻辑上似是而非。本文针对其中一些较为常见的问题具体讨论如下。

2.1 水汽与降水强度问题

降水过程本质上是大气中水汽凝结、碰并的结果，即由气态水转变为大粒径的液态或固态物质降落到地面的过程(假定它在下落过程中没有被蒸发和耗散掉)。因此，大气中的水汽是降水形成的物质基础，也是判断降水强度和累计降水量的重要因子。在天气诊断分析和预报业务中，预报员常常利用大气柱内比湿的垂直积分(即整层大气水汽含量或大气可降水量)来判断暴雨或短时强降水的强度。这种思路是否真的合乎科学逻辑呢？图 1给出我国不同强度短时强降水的气候分布特征。

从我国短时降水强度大于等于20 mm·h^-1的多年平均降水日数的分布图上看到(图 1a)，其地理分布与我国年平均暴雨日数分布^[6]非常类似，也与年降水量自南向北逐渐减少的梯度分布一致。这表明我国中东部地区大多数暴雨天气过程是包含短时强降水过程的。但中国极端降水过程的降水强度分布特征则截然不同^[7-9]，南北最强对流过程中的极端降水强度差异并不大，我国极端短时强降水事件的最大平均降水强度的区域主要位于华南南部和华北地区(图 1b)，华南北部至江南地区虽然暴雨过程多发，但该区域极端降水强度远小于华北地区，而华北京津冀地区年降水量大多只有江南地区年降水量的1/3左右，出现暴雨事件的频数也低很多，但该区域极端降水的平均强度却远大于江南地区。

上述气候特征表明，一般性短时强降水和暴雨的发生频率与大气含水量或大气可降水量联系紧密，但短时强降水强度的决定性因素可能并不是大气可降水量。其原因何在？

为了简化问题，暂不考虑降水的持续性，只讨论瞬时降水强度。对于大尺度运动，由式(3)可知，降水强度(R_L)主要决定于大气柱内水汽通量散度的垂直积分，或由式(2)可知，取决于净水汽平流的垂直积分，也就是说，大尺度降水强度并不取决于整层大气可降水量。即

$ {{R}_{L}}=\int_{{{p}_{0}}}^{p}{-\nabla \cdot \left( q\vec{v} \right)\text{d}\mathit{p}} $

或由式(2)可知${{R}_{L}}=\int_{{{p}_{0}}}^{p}{-\left( \vec{v}\cdot \frac{\partial \mathit{q}}{\partial \mathit{\vec{s}}} \right)\text{d}\mathit{p}}$

由于大气中水汽主要集中在低层，因此，对流层低层的净水汽平流或水汽通量辐合强度是判断大尺度降水强度的核心因子。当然，为了维持水汽平流或水汽通量辐合强度，降水区外侧的水汽输送通道(即水汽通量)尤显重要，即它是决定强降水能否维持的因子。

对对流过程来说，表面上看, 降水强度(R_C)与气柱内大气可降水量直接相关(R_c = Eqw)，但就其本质而言，由式(2)可知，对流降水强度取决于水汽垂直梯度和对流速度，即${{R}_{\text{c}}}\propto -w\frac{\partial q}{\partial \mathit{z}}$。由于实际对流过程中，无法准确判断气块是从哪一高度上被抬升的，这里选取一种最简单的方式来讨论:假定在自由对流高度之下的抬升作用不足以克服对流抑制能(CIN)，低层气块在开始阶段无法参与对流过程(如高架雷暴)，气块从自由对流高度(LFC)开始对流(通过CAPE的释放使气块获得向上的垂直运动)，这样就可大体判断初始对流的瞬时降水强度。然而，一旦对流启动后，雷暴中强烈的上升运动必然造成低层气流强烈辐合，近地面层水汽最终必然参与对流降水过程。

以北京地区两次局地深对流(最大雷达反射率强度均超过60 dBz，对流高度均超过10 km)短时强降水为例，粗略说明水汽、水汽垂直梯度、理论对流上升速度或对流有效位能等因素对降水强度的影响。两次过程的最大降水中心均位于北京西部山前石景山区模式口站，最大雨强分别为128 mm·h^-1(2011年6月23日16— 17时)和72 mm·h^-1 (2006年7月9日21—22时)。

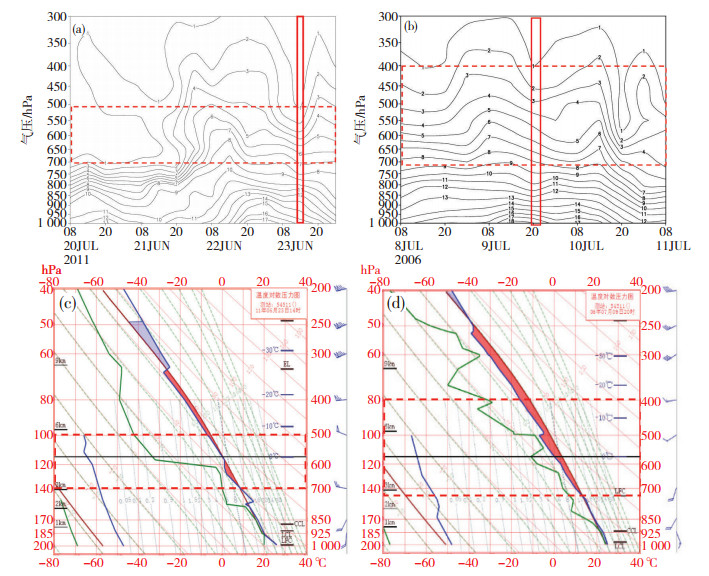
图 2a、b是利用NCEP 1°×1°最终分析资料(FNL)计算的北京区域平均(115.4°—117.5°E，39.4°—41.1°N)的比湿随时间演变图(6 h分辨率)，这代表了北京地区水汽分布的平均状态。图中红柱代表最接近强降水发生之前的大气水汽分布(一旦对流发生，由于强烈的垂直运动将极大地改变水汽的垂直分布状况，降水过程中其垂直分布特征不能代表对流启动时刻的大气状态)。图 2c、d是最靠近对流发生时刻之前的北京地区实际探空分析。图中红色虚框线的下边界对应自由对流高度(之上CAPE＞0)，上边界对应区域平均比湿q≤1 g·kg^-1的高度，大体表示位于该高度之上的气柱绝对水汽含量很少，对对流降水强度的实际贡献可以忽略。

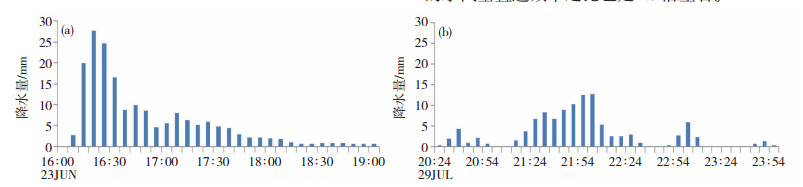
对比两次短时强降水发生前的大气状态发现: 2006年7月9日的CAPE值更大，理论上的最大云中上升速度(w_max)约为46.7 m·s^-1；而2011年6月23日w_max为28.4 m·s^-1。如果对比q≤1 g·kg^-1以下的CAPE(红色虚框包含的CAPE面积)，两者对应的理论上升速度之比更大。另一方面，无论是从实际探空还是最终再分析资料都可看到，2006年7月9日对流发生前整层大气含水量明显大于2011年6月23日，从实际探空的近地面层露点温度也可看到这种差异，2006年7月9日20时地面露点温度达到23 ℃，而2011年6月23日14时的露点温度仅20 ℃。也就是说，对流发生前，前者的wq远大于后者。但2011年6月23日对应的对流降水的小时强度反而显著大于2006年7月9日的雨强。从北京模式口自动站观测看到(图 3)，最大瞬时雨强之间的差距更是达到1倍以上: 2011年6月23日16:06— 16:18降水强度达到52.4 mm·(12 min)^-1，而2006年7月9日21:48—22:00的降水强度则为25.4 mm·(12 min)^-1。

图 3中两次过程降水强度差异可从两者的水汽垂直递减率上找到原因。对流发生前，CAPE≥0到区域平均比湿q ≤1 g·kg^-1所在高度区间的水汽垂直递减率(∂q/∂p)，2011年6月23日14时为0.03 g·(kg·hPa)^-1，2006年7月9日20时为0.02 g·(kg·hPa)^-1；从1 000 hPa高度到区域平均比湿q ≤1 g·kg^-1所在高度计算，两者的水汽垂直递减率之比也是1.5倍左右。

综上所述，虽然一定的大气可降水量是形成暴雨或短时强降水的必要条件，但对非对流降水(层状云)过程而言，对流层低层的净水汽平流量或水汽通量辐合的强度是判断降水强度的核心因子；对对流过程而言，如果不考虑蒸发过程，瞬时降水强度主要取决于水汽垂直递减率和低层大气对流有效位能的大小。

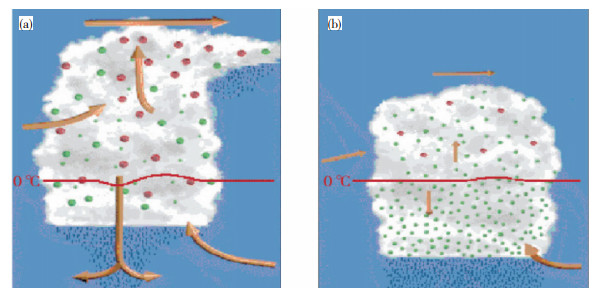
2.2 对流系统形态与层结对降水强度的影响

不考虑凝华和耗散过程，地面降水强度是云中凝结和蒸发共同作用的最终结果^[10]。因此，实际有效凝结率是影响地面降水强度的重要因素之一，而对流系统的形态特征对实际有效凝结率有重大影响。对所谓大陆对流性降水(高质心降水回波，如图 4a)过程而言，由于对流云底较高，雨滴在下落过程中(穿过非饱和大气区)存在大量的蒸发(形成地面上的雷暴高压和冷池)。另一方面，在存在较大风切变背景下，云毡下方存在更深厚的非饱和层，雨滴在下落过程中也基本上完全被蒸发。这正好说明弱的垂直风切变更有利于高降水效率，因为倾斜结构的对流云中凝结形成的固态或液态水由于存在大量的蒸发过程，而不可能完全形成有效的地面降水；相反，热带型降水回波(低质心降水回波，如图 4b)蒸发量很小，因而其实际降水效率更高。

对流系统形态特征由对流环境决定。因此，对流发生前的大气层结状态和环境风垂直切变对于预判对流降水强度具有重要的科学价值。下文以发生在济南和北京的两次短时强降水强对流天气过程为例进行说明。

2007年7月18日傍晚，位于华北南部的山东省济南市发生一次极端性特大暴雨过程，其中最大雨强达到151 mm·h^-1，造成重大人员伤亡。2008年7月4日傍晚开始，北京市东北部出现一次以“列车效应”为特征的大暴雨天气过程，其最大过程累积降水量达到132 mm (顺义区南法信镇)，其中当日18:42—19:42雨强最大达56 mm·h^-1。

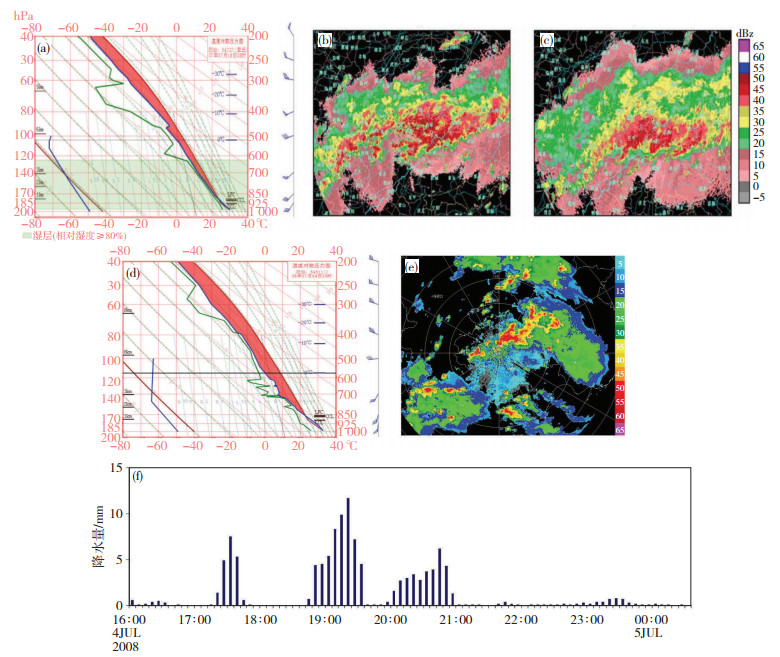
比较上述两次对流发生前的探空曲线(图 5a、d)看到，其对流过程均发生在极不稳定环境大气中，对流层低层大气饱和程度不同，但700 hPa以下绝对水汽含量相当，即1 000 hPa露点温度均为25 ℃，700 hPa附近露点温度约为10 ℃。尽管2007年7月18日傍晚济南最大雨强对应的最大反射率只有45~50 dBz (图 5b、c)，而2008年7月4日强降水发生时刻对应的雷达反射率达到50~60 dBz (图 5e)，但济南的最大小时雨强约为北京顺义(图 5f)的3倍。降水强度为什么出现如此大的差异呢？对其分析如下。

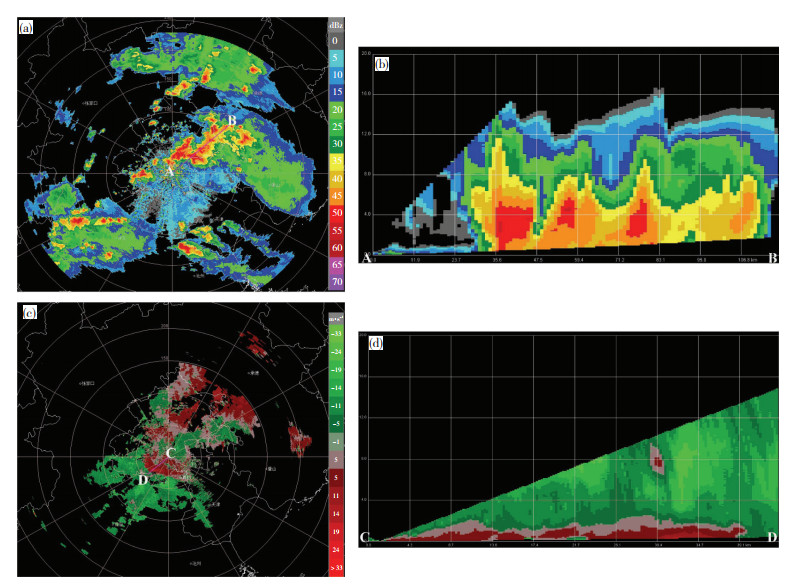
首先，从探空对应的垂直风切变看到，济南对流层中下层为一致的西南风，500—925 hPa的风速差仅为4 m·s^-1，即是一种弱切变环境下的对流降水，对应的降水回波表现为热带海洋降水型；而北京地区降水发生时，500 hPa为16 m·s^-1的西风，对流层低层(925— 850 hPa)为南风，风速达到10~14 m·s^-1，500—925 hPa的矢量风速差达到18.9 m·s^-1，是一种强切变环境下的对流过程，对应的雷达回波图上表现为倾斜结构的深对流(图略)，由于强烈的蒸发效应降低了地面降水效率，这种强烈的蒸发过程可从图 7d中阵风强度得到印证。

其次，在降水发生前，济南地区的对流层低层几乎完全饱和，抬升凝结高度(LCL)接近地面，造成云底以下几乎不可能出现明显蒸发；而北京地区对流层低层温度露点差达到6~7 ℃，LCL约为900 hPa，强降水开始阶段云底高度以下必然存在较为强烈的蒸发过程，实际上，北京顺义地区18时(初始对流阶段)最大小时雨强仅为30 mm·h^-1左右。

2.3 降水的持续时间

一次天气过程造成某地累计降水量大小的另一决定性因子是降水持续时间。对于天气尺度系统造成的大范围层云降水过程，降水持续时间取决于天气系统的移动速度，更确切地说，是降水区域上空水汽辐合维持时间的长短。

对于对流降水过程而言，降水持续时间取决对流系统的尺度、移动速度(movement)和传播(propaga⁃ tion)。中尺度对流系统水平尺度越大，其生命史越长，造成降水的持续时间也越长，如超级单体和一般对流单体相较而言，其不仅降水强度更大，且其生命史更长。对于线状对流雨带，其一般都由多单体构成: 1)如果线状对流系统的移动方向基本上与线状对流的主轴方向垂直(如快速移动的飑线系统)，则在任何点上都不会产生长时间持续降水；2)如果对流雨带移动速度矢量平行于其主轴的分量很大，则经过某一点需要更多的时间，导致更大累计雨量；3)当对流雨带的移动速度矢量基本平行于其主轴，使得对流雨带中的每一个强降水单体依次经过同一地点，形成“列车效应(Train Effect)”，就会产生极大累积雨量^{[3, 10]}。极端强降水事件大多都有“列车效应”的作用，如北京“7·21”特大暴雨^[11-12]。

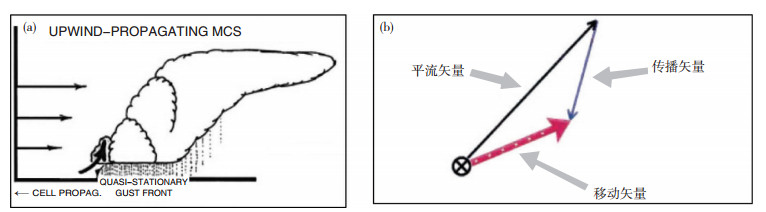
对流系统的新生和传播是形成长生命周期对流系统的重要机制。对流系统产生的冷池和出流在不稳定环境背景中极易触发新生雷暴(图 6a)。另外，移动缓慢或准静止的锋面、地形强迫作用、低空急流中的风速辐合、垂直切变不稳定等，都可能触发新生雷暴。对流系统的移动是由对流云高度层内的合成风矢量(环境风矢量)的风向风速决定的^[17]，传播是指新生对流相对于平均环境风矢量而言的，如果平均风方向(平流方向)与传播方向交角大于90°，则称为后向传播(Back-Building或Upwind-Propagation)。也就是说，后向传播存在相对于平均风矢量的逆向发展过程，此时对流回波移速小于平均风速(图 6b)，移动较慢，易导致强降水。

图 7是一次典型的后向传播过程“ (列车效应”)，该过程形成的间歇性短时强降水造成北京顺义地区大暴雨。从图 5f看到，先后有3个强降水单体经过顺义本站。由于500 hPa以下的平均环境气流为西南偏南风(SSW)，所以雷暴单体向东北方向移动，但雷暴形成了向南的低层出流，从低仰角雷达经向速度图上(图 7b)看到，在雷达站南侧存在明显离开雷达的东北偏北风(NNE)，出流风的高度在1 km以下，由于出流风(NNE)与环境风(SSW)的强烈辐合不断触发新生对流，发生后向传播现象，新老单体在环境气流的引导下形成“列车效应”。

3 结论

针对在实际预报业务和天气研究过程中将暴雨和短时强降水混为一谈或从暴雨预报方法直接引入用于短时强降水强度预报的问题，本文从水汽方程的尺度分析入手，讨论了不同尺度、不同性质的降水过程中降水强度的动力学主导因子，揭示了暴雨和短时强降水预报分析中两者的区别和联系。主要结论如下：

(1) 虽然一定的大气可降水量是形成暴雨或短时强降水的必要条件，但对于非对流大尺度降水(层状云)过程，对流层低层的净水汽平流量或水汽通量辐合的强度是判断降水强度的核心因子，这也是大范围暴雨预报分析过程中的关键因素；对于中尺度层云降水过程，水汽垂直输送量和气柱内水汽的净平流量则同等重要。

(2) 对于对流过程，如果不考虑蒸发过程，瞬时降水强度主要决定于水汽垂直递减率(而非整层大气可降水量)和低层大气对流有效位能(不是整层大气的CAPE)。假设两次对流天气过程发生前，对流层低层的CAPE相当，整层大气可降水量也相当，那么上干下湿的环境大气对应的瞬时降水强度比整层饱和环境下的降水强度更大；如果整层大气可降水量和比湿的垂直递减率均相同，且整层大气的CAPE也相同，那么，自由对流高度(LFC)越低或低层CAPE越大的环境大气，对流开始时瞬时降水强度要远大于LFC很高或低层对流抑制能(CIN)很大的对流环境。

(3) 降水强度与实际有效凝结率密切相关，而有效凝结率(形成地面有效降水)是与云的结构特征直接相关的。如对流云底相对较高且表现为回波倾斜角度很大的深对流(典型的大陆型对流系统)，由于存在较强的蒸发过程，其降水效率要远低于热带型对流降水(低质心的垂直型回波)，这是临近预报中开展降水强度判断的主要依据。从另一角度看，对流云的形态特征是由大气层结状态和环境风垂直切变决定的，这是在对流发生前预判对流降水强度的重要依据之一:干侵入(对流层中层干空气后侧入流)越强、对流层低层温度露点差越大(或抬升凝结高度LCL越高)、垂直切变越强的深对流过程，其实际降水强度远小于低质心的垂直型回波。

(4) 对于天气尺度系统造成的大范围层云降水过程，降水的持续时间取决于天气系统的移动速度，更确切地说，是降水区域上空水汽辐合维持时间的长短；对于对流降水过程，降水持续时间则取决于对流系统的尺度、移动速度(movement)和传播(propagation)。即:对流系统尺度越大，持续时间越长；对流系统的新生和传播是形成长生命周期对流系统的重要机制，由于后向传播的对流系统存在相对于平均风矢量的逆向发展过程，造成对流回波移速小于平均风速，即移动较慢，易导致持续性强降水。