2. 山东财经大学 山东省数字媒体技术重点实验室, 济南 250014;
3. 山东大学 数学学院, 济南 250100
2. Shandong Key Laboratory of Digital Media Technology, Shandong University of Finance and Economics, Jinan 250014, China;
3. School of Mathematics, Shandong University, Jinan 250100, China
股票市场行情预测一直是投资者迫切关注的话题,然而股票数据具有高噪声、动态、非线性和非参数等特点[1],准确地预测股票价格仍是一项具有挑战性的工作。随着人工智能技术的发展,深度学习以其在机器翻译[2]、语音情感识别[3]、图像识别[4]等方面的优异表现受到广泛关注。与传统统计模型相比,深度神经网络(DNN)可以通过分层特征表示来分析深层和复杂的非线性关系,适合处理股票数据分析这种多因素影响、不稳定、复杂的非线性问题。
循环神经网络(Recurrent Neural Network,RNN)将时序的概念引入到网络结构设计中,使其在时序数据分析中表现出更强的适应性。Hochreiter和Schmidhuber通过对RNN网络单元结构进行改进提出了长短期记忆(Long Short-Term Memory,LSTM)模型[5],通过设计控制门结构弥补了RNN的梯度消失和梯度爆炸、长期记忆能力不足等问题,使得RNN能够真正有效地利用长距离的时序信息[6]。目前,LSTM神经网络已经成功应用于语音识别[7-8]、文本处理[8]等方面,基于LSTM神经网络在这些方面的优异表现,应用其对金融时间序列进行研究受到广泛关注。2015年,Chen等[9]使用LSTM模型预测了中国股票市场的股票价格;2016年,Jia[10]验证了LSTM模型预测股票价格趋势的有效性;2017年,Nelson等[11]基于股票历史数据和技术指标使用LSTM模型预测了未来股票市场趋势,并与其他机器学习方法进行比较,该实验表明LSTM预测模型具有更高的预测精度;2018年,Fischer和Krauss[12]应用LSTM模型对标准普尔500指数波动情况进行预测,与随机森林(RAF)、DNN和逻辑回归分类器(LOG)相比LSTM模型具有较好的预测效果。
与其他神经网络模型类似,LSTM神经网络模型中部分参数需要人为设置,如时间窗口大小、批处理数量、隐藏层单元数目等。这些参数直接控制网络模型拓扑结构,不同参数训练出模型的预测性能差异巨大,因此选择合适的模型参数就显得尤为重要。目前,对于网络模型超参数的选择往往依赖研究者的经验和多次实验结果,耗费大量的人力和计算资源。因此,本文提出一种基于自适应粒子群优化(PSO)的LSTM股票价格预测模型(PSO-LSTM),利用自适应学习策略的PSO算法对股票数据特征与LSTM神经网络拓扑结构进行匹配,获得更高的预测性能。在此基础上,本文选取沪市浦发银行、深市五粮液、港股恒隆集团股票数据,构建PSO-LSTM模型对第2日股票收盘价进行预测。
1 相关工作 1.1 LSTM神经网络LSTM是一种特殊的循环神经网络。它通过精心设计“门”结构,避免了传统循环神经网络产生的梯度消失与梯度爆炸问题,能有效地学习到长期依赖关系。因此,在处理时间序列的预测和分类问题中,具有记忆功能的LSTM模型表现出较强的优势。
如图 1所示,LSTM是由多个同构单元格组成,该结构能够通过更新内部状态来长时间存储信息,A表示3个单元具有相同的单元结构。每个单元格由4个主要元素构成:输入门、遗忘门、输出门和单元状态。
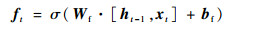
|
(1) |
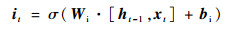
|
(2) |
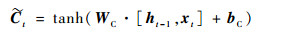
|
(3) |

|
(4) |
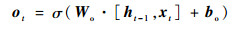
|
(5) |
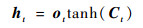
|
(6) |

|
| 图 1 LSTM单元结构 Fig. 1 LSTM unit structure |
式中:x为LSTM单元的输入向量;h为单元格输出向量;f、i、o分别表示遗忘门、输入门和输出门;C表示单元状态;下标t表示时刻; σ、tanh分别为sigmoid、tanh激活函数;W和b分别表示权重和偏差矩阵。
LSTM的关键是单元状态C,它在t时刻保持单元状态的记忆,通过遗忘门ft和输入门it进行调节。遗忘门的作用是让细胞记住或忘记它之前的状态Ct-1,输入门的作用是允许或阻止传入信号更新单元状态。输出门的作用是控制单元状态C输出和传输到下一个单元格。LSTM单元的内部结构是由多个感知器构成的,反向传播算法通常是最常见的训练方法。
1.2 传统粒子群算法粒子群算法的思想源于对鸟类社会行为的研究。鸟群捕食最简单有效的方法是搜索距离食物最近的鸟的所在区域,通过个体间的协助和信息共享实现群体进化。算法将群体中的个体看作多维搜索空间中的一个粒子,每个粒子代表问题的一个可能解,其特征信息用位置、速度和适应度值3种指标描述,适应度值由适应度函数计算得到,适应度值的大小代表粒子的优劣。粒子以一定的速度“飞行”,根据自身及其他粒子的移动经验,即自身和群体最优适应度值,改变移动的方向和距离。不断迭代寻找较优区域,从而完成在全局搜索空间中的寻优过程。
传统粒子群算法描述为:假设在一个D维搜索空间,m个粒子构成的一个种群X={x1, x2, …, xm},其中xi=[xi1, xi2, …, xiD],设t时刻xi的特征信息为
位置:Xit=[xi1t, xi2t, …, xiDt]T
速度:Vit=[vi1t, vi2t, …, viDt]T
个体最优位置:pit=[pi1t, pi2t, …, piDt]T
全局最优位置:pgt=[pg1t, pg2t, …, pgDt]T
则该粒子在t+1时刻的速度和位置信息更新:
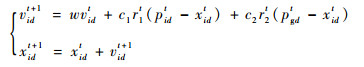
|
(7) |
式中:w为惯性权重,控制粒子在全局探测和局部开采间的有效平衡;c1和c2为学习因子,分别调整飞向自身和全局最好位置方向的步长;r1和r2为均匀分布在[0, 1]之间的随机数。为避免粒子搜索,一般将其速度和位置分别限制在[-Vmax, Vmax]和[-Xmax, Xmax]之内。
2 自适应PSO的LSTM神经网络预测模型 2.1 自适应学习策略的PSO算法本文借助聚类思想,根据粒子自身的分布情况,将整个种群自适应地划分成若干子群[13]。对于每个子群,采用不同的学习策略分布对不同类型的粒子进行更新,提高种群多样性。
采用一种具有较高聚类性能的快速搜索聚类方法实现子群的划分[14]。该方法能自动发现数据集样本的类簇中心,同时能够实现任意形状数据集样本的高效聚类。其基本原理是:类簇中心具备2个基本特征,被局部密度较低的点包围,且与局部密度较高的点距离较大。
在一个D维搜索空间中,由h个粒子构成的一个种群S={xi}i=1h,其中xi=[xi1, xi2, …, xiD],对于第i个粒子的第d维给出2个变量,粒子的局部密度ρid与到更高局部密度粒子间距离δid,其定义为
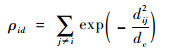
|
(8) |
式中:dij为xid和xjd之间欧氏距离;dc为截断距离。

|
(9) |
对于局部密度ρid最大的样本,其δid=maxj(dij)。
由式(9)可知,若xid的密度是最大局部密度,则δid远大于其最邻近粒子的δ距离。因此,子群的中心往往是δ异常大的粒子,这些粒子的密度ρ也相对较高,即选择ρ和δ都较大的粒子作为聚类中心。对于其他粒子的xjd,将其归入密度比xjd大且距离xjd最近的样本所在的子群。
基于子群划分的结果,将每个子群中的粒子分为普通粒子和局部最优粒子两类。对于普通粒子,其主要在子群中最优粒子的引导下拓展局部搜索能力,更新公式为
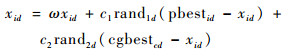
|
(10) |
式中:ω为惯性权重;c1、c2为学习因子;rand1d、rand2d为区间[0, 1]上的均匀分布随机数;pbestid为第i个粒子第d维的最优位置信息;cgbestcd为第c个子群中的最优位置信息。
对于局部最优粒子,其主要通过综合各子群的信息进行更新,以加强子群间的信息交互,更新公式为
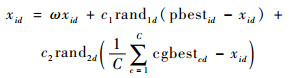
|
(11) |
局部最优粒子一方面指导普通粒子的学习,另一方面作为子群间信息交互的媒介。在子群中,局部最优粒子引导着整个子群的搜索方向,若采用式(10)的学习策略,一旦局部最优粒子偏离最优解的搜索方向,会导致整个子群陷入局部最优。因此,局部最优粒子需要突破子群的控制,从其他子群中获得信息。考虑到局部最优粒子是子群中最有可能找到最优解的粒子,式(11)利用各个子群中局部最优粒子的平均信息来指导粒子的更新。通过这种子群间信息的共享,促进子群间寻优信息的传递,进一步提高种群的多样性,避免陷入局部最优。
2.2 PSO-LSTM模型股票数据作为一种金融时间序列,其受到多方面因素的影响,具有复杂的不稳定性、非线性与周期不确定性。为了准确地预测股票价格,本文以在时间序列分析中表现优异的LSTM模型为基础,构建针对股票数据的预测模型。LSTM模型中某些超参数的取值控制着模型网络结构,为了使模型网络结构与股票数据特征相匹配,本文将自适应PSO算法与LSTM模型相融合,构建了PSO-LSTM预测模型。
PSO算法相较于其他生物智能演化算法的最大优势在于算法设计简单、收敛速度快,但易陷入局部最优。自适应PSO算法能够根据种群自身的分布,通过自适应的子群划分和粒子更新来避免局部最优,提高参数寻优的准确性。自适应PSO算法的自适应特性使得LSTM模型能够根据股票数据的特征,快速、准确地确定最优超参数,实现LSTM模型网络结构与股票数据特征的有效结合。
模型首先将时间窗口大小、批处理大小、隐藏层单元数目作为自适应PSO算法的优化对象,根据超参数取值范围随机初始化各粒子位置信息。通过式(8)、式(9)计算得到粒子的局部密度ρid及其到更高局部密度粒子的距离δid,实现自适应种群划分。
其次,根据粒子位置对应的超参数取值建立LSTM模型,利用训练数据对模型进行训练。将验证数据代入训练好的模型进行预测,以模型在验证数据集上的平均绝对百分比误差作为粒子适应度值。
适应度函数f定义为
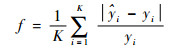
|
(12) |
式中:K为验证数据集的数量;
根据各子群中粒子适应度值的取值情况,将粒子划分为普通粒子、子群局部最优粒子与全局最优粒子。通过式(10)、式(11)分别对不同类别粒子位置信息进行更新。判断是否达到终止条件,达到终止条件即得到优化目标的最优值;否则,重新根据粒子位置信息进行种群划分,计算各粒子适应度值,更新各粒子位置信息,直到满足终止条件。
最后,以超参数最优值构建LSTM模型,通过股票数据进行训练和预测。PSO-LSTM模型架构如图 2所示。
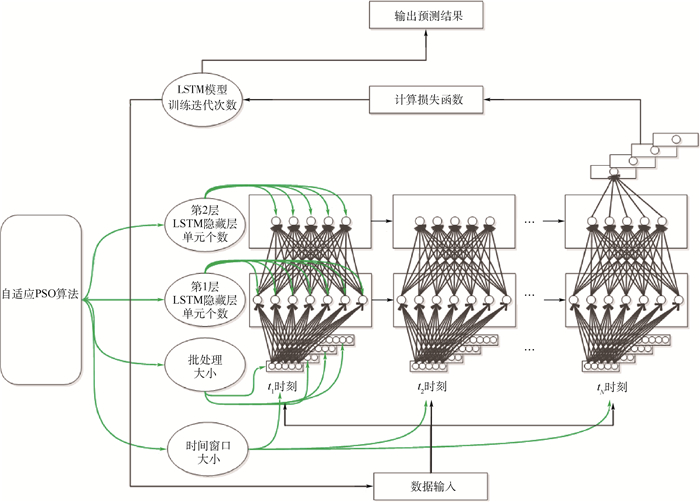
|
| 图 2 PSO-LSTM模型架构 Fig. 2 PSO-LSTM model architecture |
PSO-LSTM模型算法流程如下:
步骤1 将实验数据分为训练数据、验证数据和测试数据。
步骤2 将LSTM模型中时间窗口大小、批处理大小、神经网络隐藏层单元数目作为优化对象,初始化自适应PSO算法。
步骤3 根据式(8)、式(9)划分子群。
步骤4 根据式(12)计算每个粒子的适应度值。以各粒子对应参数构建LSTM模型,通过训练数据进行训练,验证数据进行预测,将预测结果的平均绝对百分比误差作为各粒子的适应度值。
步骤5 根据粒子适应度值与种群划分结果,确定全局最优粒子位置pbest和局部最优粒子位置gbest。
步骤6 根据PSO算法的式(10)、式(11)分别对普通粒子和局部最优粒子位置进行更新。
步骤7 判断终止条件。若满足终止条件,返回最优超参数取值;否则,返回步骤3。
步骤8 利用最优超参数构建LSTM模型。
步骤9 模型通过训练数据和验证数据进行训练,测试集进行预测,得到预测结果。
3 实验与结果实验选取沪市A股(600000浦发银行)、深市A股(000858五粮液)、港股(00010恒隆集团)为例进行研究,预测股票第2日收盘价格。股票历史数据包含开盘价、收盘价、最高价、最低价、涨幅、振幅、成交量、成交额、换手率以及成交次数10个属性。其中可能包含停盘停等操作所造成的数据空缺,对于空缺数据进行删除操作,并按时间对数据进行排序。建立PSO-LSTM模型并与自回归移动平均模型(ARIMA)[15]、支持向量机(SVM)[16]、多层感知机(MLP)[17]、RNN[18]和LSTM[19]模型进行对比实验。
3.1 模型评价标准本文选取均方根误差(RMSE)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)、均方误差(MSE)和决定系数R2作为评价指标对模型预测效果进行定量评价。其中RMSE、MAPE、MAE、MSE数值越小,模型预测结果与真实值偏差越小,结果越准确;决定系数R2越接近1,代表拟合优度越大,模型预测效果越好。具体公式定义为
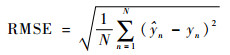
|
(13) |

|
(14) |
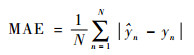
|
(15) |
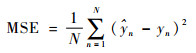
|
(16) |

|
(17) |
式中:N为实验预测次数;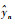
PSO-LSTM模型结构由输入层、两层LSTM层、输出层组成,损失函数使用均方误差,模型训练过程采用Adam算法进行优化,网络模型的搭建在Keras框架下实现。该模型将时间窗口大小、批处理大小、训练次数和隐藏层单元个数设置为LSTM模型超参数。为了减少人为因素对模型的影响,实验根据股票数据具体情况,对超参数的取值范围设置如下:指定时间窗口大小取值范围[1,20],批处理大小取值范围[1,60],隐藏层单元个数取值范围[10,30]。同时设置粒子群粒子个数为30,最大迭代次数为500,速度惯性权重ω为0.8,加速系数和为2。
PSO-LSTM训练次数由模型误差损失情况直接确定,模型迭代到800次时误差损失函数达到收敛状态。因此PSO-LSTM模型的训练次数为800。
3.3 实验分析 3.3.1 沪市股票预测浦发银行2016-01-04—2018-12-21日K数据共计708条,其中70%作为训练数据、20%作为验证数、10%作为测试数据。自适应PSO模型的最优超参数为:时间窗口大小为10,批处理大小为58,第1层隐藏层单元个数为12,第2层隐藏层单元个数为22。实验结果如图 3所示:绿色实线表示测试数据的股票收盘价真实值,红色实线表示不同预测模型的股票收盘价预测值。预测结果显示ARIMA模型预测值曲线在趋势上非常符合股价真实值,然而在每个时间点处的预测值与真实值之间总保持一定误差,具有明显的滞后性。这是由于ARIMA模型采用了分步预测方法,每个时间点的预测值均为历史时刻的真实值预测产生。因此ARIMA模型预测曲线总是落后于股价真实值曲线说明ARIMA模型的预测效果并不好,其预测精度可由模型评价指标进行比较;从其他模型预测结果来看,本文提出的PSO-LSTM模型的预测曲线更接近股价真实值曲线,特别是在股价波动剧烈处的预测效果优于其他模型。

|
| 图 3 上海浦发银行各模型预测结果比较 Fig. 3 Comparison of prediction results of various models for Shanghai Pudong Development Bank |
为进一步验证该模型的预测性能,表 1给出各预测模型的评价指标计算结果。PSO-LSTM模型预测误差在RMSE、MAPE、MAE、MSE评价标准下都低于其他预测模型;在决定系数R2评价标准中,该模型计算结果比其他预测模型更接近1,表明PSO-LSTM模型的预测性能优于其他模型。特别地,PSO-LSTM模型MAPE指标比ARIMA模型低71%,比RNN模型低31%,模型预测精度显著提高;PSO-LSTM模型的各项指标优于LSTM模型,但两者差距并不明显,主要原因是这两种预测模型具有相同的单元结构;而PSO-LSTM模型最突出的优势在于构建过程中不需要人工调参,而且预测结果比普通LSTM模型更优。
| 模型 | RMSE | MAPE/% | MAE | MSE | R2 |
| ARIMA | 0.1609 | 3.6176 | 0.3809 | 0.0259 | 0.9833 |
| SVM | 0.1847 | 1.4149 | 0.1482 | 0.0341 | 0.9666 |
| MLP | 0.1924 | 1.4665 | 0.1551 | 0.0374 | 0.9832 |
| RNN | 0.2082 | 1.5145 | 0.1598 | 0.0433 | 1.3423 |
| LSTM | 0.1799 | 1.3792 | 0.1451 | 0.0323 | 1.1518 |
| PSO-LSTM | 0.1420 | 1.0369 | 0.1068 | 0.0202 | 1.0120 |
为了进一步研究该模型与传统LSTM模型的有效性与稳定性,实验将浦发银行2018-12-24—2019-03-12日的日K数据平均分成5组,分别利用LSTM模型和PSO-LSTM模型进行预测,预测结果如图 4所示。图中:绿色曲线表示股价真实值,蓝色曲线表示LSTM模型预测值,红色曲线表示PSO-LSTM模型预测值。从图中可以看出,对于第2组、第3组和第5组数据,PSO-LSTM模型的预测值曲线比LSTM模型更逼近股价真实值曲线。对于第1组和第4组数据,PSO-LSTM模型与LSTM模型的预测结果非常接近。

|
| 图 4 LSTM与PSO-LSTM预测结果比较 Fig. 4 Comparison of prediction results between LSTM and PSO-LSTM |
表 2给出两种预测模型的RMSE指标比较结果。除了在第1组数据中LSTM模型的RMSE指标具有微弱优势,PSO-LSTM模型在其他4组数据预测的RMSE指标都优于LSTM模型。特别地,在第5组数据测试中PSO-LSTM模型的预测精度比LSTM模型高了25%。实验结果表明,本文提出的PSO-LSTM模型对于不同时段的浦发银行股票价格均有较好的预测能力,在模型预测精度与模型预测稳定性方面比LSTM模型更具优势。
| 模型 | RMSE | ||||
| 第1组 | 第2组 | 第3组 | 第4组 | 第5组 | |
| LSTM | 0.1072 | 0.1061 | 0.1442 | 0.1629 | 1.1534 |
| PSO-LSTM | 0.1174 | 0.0913 | 0.1361 | 0.1240 | 0.1149 |
3.3.2 深市股票预测
五粮液2016-01-04—2018-12-21的日K数据共计726条,其中70%作为训练数据、20%作为验证数、10%作为测试数据。自适应PSO模型的最优超参数为:时间窗口大小为12,批处理大小为60,第1层隐藏层单元个数为16,第2层隐藏层单元个数为32。实验结果如图 5所示。
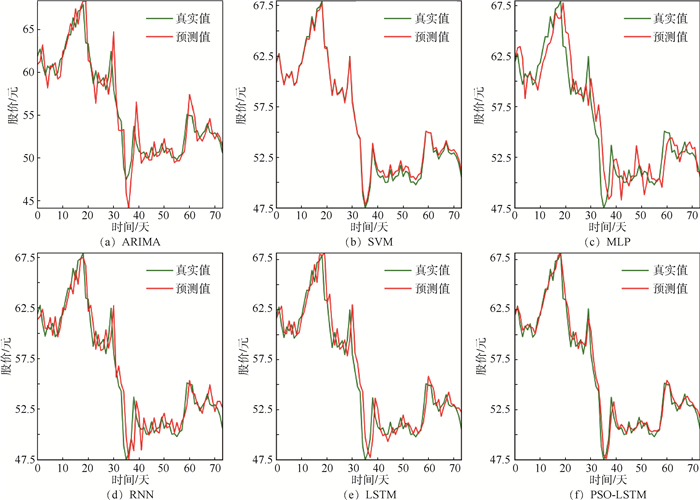
|
| 图 5 五粮液各模型预测结果比较 Fig. 5 Comparison of prediction results of various models for Wuliangye |
如图 5所示,ARIMA模型在股票价格持续上涨或下跌时刻的预测效果较好,预测值接近股价真实值。但是在股价变化剧烈的时刻,ARIMA模型预测结果具有一定的延后性;SVM模型在股价波动剧烈时刻的预测效果较差,预测曲线与真实值之间具有明显的误差;LSTM模型的预测效果优于MLP模型与RNN模型;对于五粮液股票价格的预测,PSO-LSTM模型的预测效果最好,其预测值曲线能较好地逼近股价真实值。表 3给出不同预测模型评价指标的比较结果,PSO-LSTM模型除评价指标均优于其他预测模型。
| 模型 | RMSE | MAPE/% | MAE | MSE | R2 |
| ARIMA | 1.7814 | 11.1753 | 6.2734 | 3.2851 | 1.0178 |
| SVM | 1.6896 | 2.4872 | 1.3764 | 2.8548 | 0.7726 |
| MLP | 1.8892 | 2.6822 | 1.3879 | 3.4882 | 1.0605 |
| RNN | 1.6549 | 2.3478 | 1.3247 | 2.7203 | 1.0344 |
| LSTM | 1.6013 | 2.1247 | 1.1918 | 2.5734 | 1.0571 |
| PSO-LSTM | 1.3427 | 1.7808 | 1.0342 | 1.8028 | 1.0124 |
3.3.3 港股股票预测
恒隆集团2016-01-04—2018-12-21的日K数据共计733条,其中70%作为训练数据、20%作为验证数、10%作为测试数据。自适应PSO模型的最优超参数为:时间窗口大小为10,批处理大小为48,第1层隐藏层单元个数为18,第2层隐藏层单元个数为24。实验结果如图 6所示。ARIMA模型在股票价格涨跌拐点处的预测结果较差,对于股票上涨或下跌趋势的预测有一定的滞后;SVM模型对于恒隆集团股票数据的预测表现最差,在某些时间点的预测结果与真实值之间具有明显的差异。相较于其他模型,PSO-LSTM模型的预测效果仍表现较好。
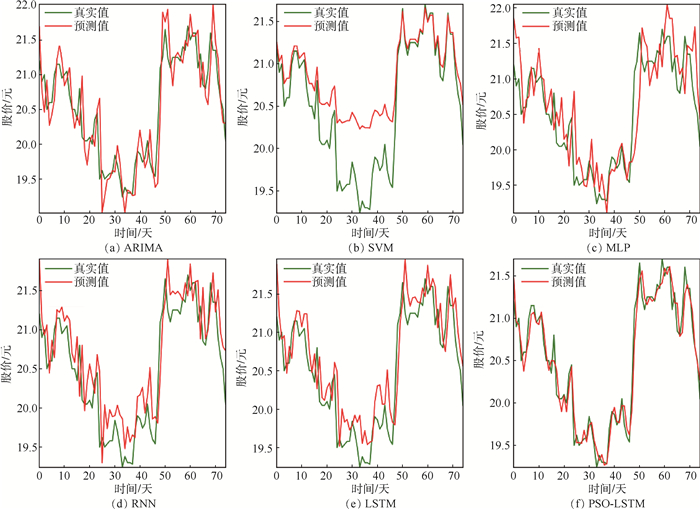
|
| 图 6 恒隆集团各模型预测结果比较 Fig. 6 Comparison of prediction results of various models for Hang Lung Group |
表 4给出不同预测模型评价指标的比较结果,PSO-LSTM模型的各项评价指标均优于其他预测模型,其中R2指标非常接近1,这说明PSO-LSTM模型对于恒隆集团股票数据的拟合最优度最佳。综合沪市、深市、港股股票的预测结果表明,PSO-LSTM模型对于股票数据的预测具有较高的预测精度与稳定性。
| 模型 | RMSE | MAPE/% | MAE | MSE | R2 |
| ARIMA | 0.3582 | 4.3628 | 0.8921 | 0.1282 | 1.2391 |
| SVM | 0.5216 | 2.1204 | 0.4247 | 0.2721 | 0.5797 |
| MLP | 0.3439 | 1.2296 | 0.2529 | 0.1183 | 0.9695 |
| RNN | 0.3844 | 1.5902 | 0.3242 | 0.1478 | 0.9568 |
| LSTM | 0.3649 | 1.4834 | 0.3026 | 0.1332 | 0.9567 |
| PSO-LSTM | 0.2845 | 1.0472 | 0.2366 | 0.0812 | 1.0041 |
4 结论
针对复杂的股票价格预测问题,本文提出了PSO-LSTM模型,通过自适应学习策略的PSO算法对LSTM网络结构进行优化,减少人为因素影响,以提高模型捕获股票数据特征的能力。本文随机选取了沪市(浦发银行)、深市(五粮液)、港股(恒隆集团)股票数据进行实验。实验表明相较于统计模型与其他时间序列机器学习模型,PSO-LSTM模型具有更高的预测精度,并且对于不用类型的股票数据具有一定的普遍适用性。该模型在金融时间序列研究中将具有广阔的应用前景。
| [1] |
SI Y W, YIN J. OBST-based segmentation approach to financial time series[J]. Engineering Applications of Artificial Intelligence, 2013, 26(10): 2581-2596. DOI:10.1016/j.engappai.2013.08.015 |
| [2] |
COSTA-JUSSÀ, MARTA R, ALLAUZEN A, et al. Introduction to the special issue on deep learning approaches for machine translation[J]. Computer Speech & Language, 2017, 46(11): 367-373. |
| [3] |
FAYEK H M, LECH M, CAVEDON L. Evaluating deep learning architectures for speech emotion recognition[J]. Neural Network, 2017, 92(2): 60-68. |
| [4] |
XING J L, LI K, HU W M, et al. Diagnosing deep learning mod- els for high accuracy age estimation from a single image[J]. Pattern Recognition, 2017, 66(1): 106-116. |
| [5] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [6] |
DEIHIMI A, ORANG O, SHOWKATI H. Short-term electric load and temperature forecasting using wavelet echo state networks with neural reconstruction[J]. Energy, 2013, 57(3): 382-401. |
| [7] |
CAI M, LIU J. Maxout neurons for deep convolutional and LSTM neural networks in speech recognition[J]. Speech Communication, 2016, 77(3): 53-64. |
| [8] |
ZHOU C, SUN C, LIU Z, et al. A C-LSTM neural network for text classification[J]. Computer Science, 2015, 1(4): 39-44. |
| [9] |
CHEN K, ZHOU Y, DAI F.A LSTM-based method for stock returns prediction: A case study of China stock market[C]//IEEE International Conference on Big Data.Piscataway, NJ: IEEE Press, 2015: 2823-2824.
|
| [10] |
JIA H J.Investigation into the effectiveness of long short term memory networks for stock price prediction[EB/OL]. (2016-03-25)[2019-07-10]. https://arxu-org/abs/1603.07893v1.
|
| [11] |
NELSON D M Q, PEREIRA A C M, DEOLIVEIRA R A, et al.Stock market's price movement prediction with LSTM neural networks[C]//International Joint Conference on Neural Networks.Piscataway, NJ: IEEE Press, 2017: 1419-1426.
|
| [12] |
FISCHER T, KRAUSS C. Deep learning with long short-term memory networks for financial market predictions[J]. European Journal of Operational Research, 2018, 270(2): 654-669. DOI:10.1016/j.ejor.2017.11.054 |
| [13] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [14] |
胡旺, 李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报, 2007, 18(4): 861-868. HU W, LI Z S. A simpler and more effective particle swarm optimization algorithm[J]. Journal of Software, 2007, 18(4): 861-868. (in Chinese) |
| [15] |
ADEBIYI A A, ADEWUMI A O, AYO C K.Stock price prediction using the ARIMA model[C]//UKSIM-AMSS International Conference on Computer Modelling & Simulation.Piscataway, NJ: IEEE Press, 2015: 106-112.
|
| [16] |
LIN Y, GUO H, HU J.An SVM-based approach for stock market trend prediction[C]//International Joint Conference on Neural Networks.Piscataway, NJ: IEEE Press, 2013: 1-7.
|
| [17] |
USMANI M, ADIL S H, RAZA K, et al.Stock market prediction using machine learning techniques[C]//International Conference on Computer & Information Sciences.Piscataway, NJ: IEEE Press, 2016: 322-327.
|
| [18] |
RATHER A M, AGARWAL A, SASTRY V. Recurrent neural network and a hybrid model for prediction of stock returns[J]. Expert Systems with Applications, 2015, 42(6): 3234-3241. DOI:10.1016/j.eswa.2014.12.003 |
| [19] |
MCNALLY S, ROCHE J, CATON S.Predicting the price of Bitcoin using Machine Learning[C]//26th Euromicro International Conference on Parallel Distributed and Network-based Processing.Piscataway, NJ: IEEE Press, 2018: 339-343.
|



