2. 航天工程大学 航天指挥系, 北京 101416
2. Department of Space Command, Space Engineering University, Beijing 101416, China
网络可视化的目的是辅助用户感知网络结构,理解和探索隐藏在网络数据内部的规律、模式等[1-2]。然而,如果将所有节点和连边的细节信息完全展示在有限尺寸的屏幕中,会导致以下问题:①受屏幕尺寸限制,对于具有大量节点和高密度连边的大规模网络可视化来说,用户会陷入混乱重叠的节点-连接图中,难以识别和感知网络的整体结构,更不能引导用户发现感兴趣的元素;②大规模的数据量必然带来更大的计算压力,对算法和硬件都会有更高的要求。低效、耗时的网络可视化就失去了应有的意义。
因此,为了达到有效展示信息和辅助用户感知网络整体结构的目的,必须对大规模网络进行一定的缩减处理,以降低用户的感知复杂度和布局过程的计算复杂度。根据缩减目的,可将网络缩减处理方法分为3类:过滤、抽样和压缩。
过滤就是通过网络中节点或连边的单个属性或多个属性的组合筛选满足条件的节点和连边,从而降低节点数量和连边密度。过滤技术更多的是在对网络结构有了一定了解的基础上,对网络数据进行的进一步细化探索,如根据节点的度、介数中心性、中介中心性及连边的权重等属性,有针对性地将满足条件的元素筛选并显示在屏幕中。
抽样是根据一定的抽样策略筛选有代表性的节点和连边,用尽可能少的节点和连边最大限度地反映原始网络的结构特征。常用的抽样策略包括随机选点、随机选边、随机游走和基于拓扑分层模型的抽样策略等[3-4]。
相对于过滤和抽样,压缩则是通过把具有一定相似性的节点或连边聚合,并采用新的节点来代替聚集,在降低节点规模的同时还能够保证网络的完整性和展示网络的子图构成等特征,更有助于用户从中观尺度感知网络整体结构[5-6]。
本文以有效展示网络的中观尺度结构特征为目标开展网络可视化压缩布局方法研究,将力导引布局算法与网络社团结构特征相结合,提出了一种基于社团结构节点重要性的网络可视化压缩布局方法。将基于拓扑势的社团结构压缩方法应用于网络拓扑结构可视化,通过原始网络的社团构成和社团内部结构等中观尺度结构的清晰展示,辅助用户分析社团和重要节点在网络结构中的位置和作用。
1 相关工作在网络可视化压缩布局方法中,由于弹簧模型[7]具有简洁高效和易于理解等优势,国内外学者基于弹簧模型对网络可视化压缩布局方法进行了大量探索。该方法将整个网络模拟为弹簧系统,通过计算节点受到的弹力控制节点间的距离最终达到节点的受力平衡。KK(Kamada-Kawai)算法[8]在弹簧模型的基础上引入胡克定律,根据节点受力状态计算系统能量,将节点最优布局问题转化为系统能量最小化的求解问题,使布局过程的收敛速度有了明显的增加。Davidson和Harel[9]在DH(Davidson-Harel)算法中考虑了节点位置、连边长度和连边交叉等多种美学标准的约束来构建能量函数,通过能量函数模型参数可达到不同的布局效果。FR(Fruchterman-Reingold)算法[10]将节点建模为物理系统中的带电粒子,将粒子间的电荷斥力引入弹簧模型,粒子间距越小斥力越大,在一定程度上降低了密集节点的重叠现象,为使算法快速收敛,通过引入“冷却函数”,采用模拟退火算法,逐步降低节点移动步长,使系统能量快速减小,从而实现快速布局的目标[11-12]。
相比于KK算法和DH算法,FR算法在大多数网络数据的可视化应用中具有更好的对称性和聚类布局效果,绘制结果更加符合美学标准,得到广泛的应用。
国内外有关网络压缩的研究主要是基于节点或者连边重要性进行压缩。Gilbert和Levchenko[5]基于节点的重要性提出了网络压缩的一般框架,该框架指出,通过删除非重要节点及与之关联的连边可以达到压缩网络拓扑的目的。王晓华等[13]基于几何多尺度分析,提出了网络数据和结构的稀疏表示方式,有效帮助人们凭借尽可能少的信息来分析网络。李甜甜等[14]基于复杂网络中的k-core概念划分网络节点,利用力导引布局算法实现压缩后的大规模复杂网络数据的布局显示。上述方法基于网络全局对节点的重要性进行评估,选择重要节点作为网络整体结构的代表节点,同时压缩非重要节点,最终实现网络压缩的目的。这类方法从节点尺度(微观尺度)上保留了网络的核心结构,但是忽略了网络的社团结构,不能从中观尺度展示网络的结构特征。
基于数据场理论,文献[15]通过计算节点的拓扑势刻画了节点在网络中受自身和邻居节点的影响多具有的势值,能够更加真实地描述节点在网络结构构成中的重要性。肖俐平等[15]和王戬[16]将其分别应用于多种真实网络数据,并于基于度、介数和PageRank等典型的节点重要性测度指标进行对比,指出拓扑势在考虑节点度重要性的同时,还能突出节点在网络中位置的差异性,在反映节点重要性方面更加精细和真实。
类似地,在同一社团结构中,不同节点对社团结构构成的贡献度不尽相同,度值越大并且离社团中心点越近的节点往往比其他节点更重要。因此,本文考虑根据节点的度和节点之间的最短路径长度确定节点在社团结构中的位置,将基于拓扑势的节点重要性评估应用于社团结构,通过选择社团结构中节点重要性高的节点作为社团结构代表节点,实现网络社团结构压缩。
2 网络可视化压缩布局方法 2.1 多粒度社团结构探测相比于其他社团结构探测算法,Louvain算法的运算速度更快,可以快速处理具有数以亿计节点的网络,另外基于层次聚类可以输出不同粒度的社团结构划分结果。因此,本文采用Louvain算法实现多粒度社团结构探测。
模块度是刻画网络中社团划分质量的重要指标之一,可通过如下公式计算:
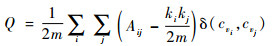
|
式中:m为网络中的连边总数;Aij为节点对(vi, vj)连边的权值;ki为节点度;cvi为节点vi隶属的社团;δ(cvi, cvj)为狄拉克函数,如果节点隶属于同一社团,则为1,否则为0。
基于模块度优化的社团结构探测算法属于凝聚算法的一种,其通过优化模块度增益函数不断地凝聚节点,最终获得社团结构划分结果。文献[17]将模块度增量函数定义为
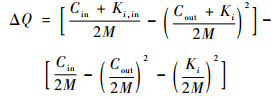
|
式中:Cin为社团C中所有内部边权重的总和;Cout为所有与社团C中节点邻接的边权重总和;Ki为所有邻接节点i的边权重的总和;Ki, in为所有从节点i与社团C中节点邻接的边权重总和;M为网络中所有边的权重之和。
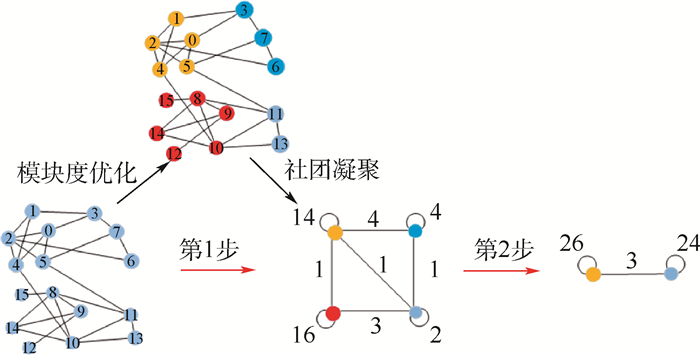
如图 1所示,Louvain算法主要分为2个阶段。首先,初始化每个节点为一个社团,不断遍历网络中的所有节点,计算该点加入到各个社团产生的模块度增量,如果模块度增量大于0,则从这些大于0的模块度增量所对应的社团中选出对应模块增量最大的社团,将该点与之合并。重复上述过程,直到网络中社团两两之间不再合并为止。然后,基于第1层社团划分结果,将每个社团抽象为“节点”,并构建新的网络,新节点之间的权重是原始网络中社团之间的权重。重复上一阶段的过程,直到社团之间不能再合并为止。
|
| 图 1 Louvain算法示意图 Fig. 1 Schematic diagram of Louvain algorithm |
节点拓扑势的大小描述了网络拓扑中的某个节点受自身和近邻节点共同影响所具有的势值。类似地,对于一个给定的社团C=(VC, EC)(VC为社团C中的所有节点集合,EC为社团C中的所有连边集合),社团中任意一个节点的拓扑势的计算公式为
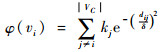
|
(1) |
式中:|VC|为社团C中的节点数量;kj越大,对节点vi的作用越大;dij为节点vi到节点vj的最短路径长度;δ为影响因子,表示节点之间的相互作用范围。
从式(1)可知,社团中任一节点的势实际上等于社团内其他所有节点对其作用力之和,并且作用力随着到节点距离的增大而逐渐衰减。社团中某点周围的节点越多,距离越短,则该节点的势就越大。因此,可以判断势值最高的节点即为处于社团中心位置的节点,该节点可以看作是社团中心节点;反之,处于社团边缘的节点往往具有的连边较少,势值相对较低。
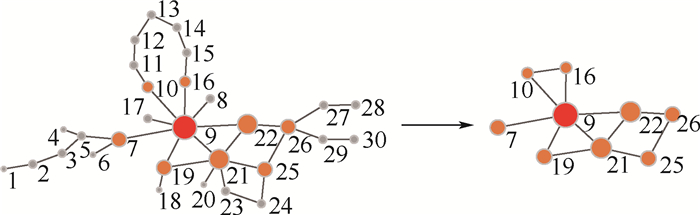
根据节点的度和节点到社团中心节点的最短路径长度确定的社团结构中节点的拓扑位置反映了节点对社团结构构成的贡献度大小。如图 2中左图所示,通过计算节点在社团结构中的势来评估节点的重要性,根据重要性排序将社团内部节点分为3类:①节点9最重要,是拓扑势极值点,也是社团中心点,图 2中左图用红色标注,用VCA表示;②节点7,19,21,22,25,26,10,16对拓扑势极值点影响较大,图 2中左图用黄色标注,用VCB表示;③其余节点为边缘节点,图 2中左图采用灰色标注,用VCC表示。选择社团中拓扑势的极值点作为社团代表点,选择对代表点拓扑势贡献大的节点作为相对重要节点。
|
| 图 2 社团节点分类与社团压缩示意图 Fig. 2 Schematic diagram of community node classification and community compression |
在社团结构压缩时,选择尽可能少的节点最大限度地保持社区结构。图 2中右图为在社团节点分类基础上对社团进行压缩后的社团结构。将社团代表点VCA和相对重要节点集合VCB作为社团结构代表点集合V′CA。社团压缩主要是为边缘节点VCC设置替代节点,从而将边缘节点与社团结构代表点合并,压缩到网络中只留下社团结构代表点。
对于vi∈VCC,用VN(vi)表示节点vi的邻居节点集合,当节点vi满足式(2)时,将节点vi和社区结构代表节点vj压缩为一个节点,并将vj设置为vi的替代节点。
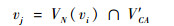
|
(2) |
采用广度优先算法为VCC集合中的节点查找并设置替代节点,具体方法如算法1所示,其中IfReplaced(vi)标记节点vi是否被V′CA中的节点代替,用replace(vi)表示节点vi的代替点。
算法1 广度优先遍历替代节点设置算法。
输入:原始节点vi、邻居节点集合VN(vi)、社团结构代表点集合V′CA。
输出:替代节点replace(vi)。
1 创建广度优先访问列表L(vi), L(vi).PUSH(VN(vi))
2 WHILE L(vi).size>0 DO
3 vj=L(vi).POP()
4 IF (vj∈V′CA)
5 replace(vi)=vj
6 IfReplaced(vi)=1
7 BREAK WHILE
8 END IF
9 ELSE
10 L(vi).PUSH(VN(vj))
11 END ELSE
12 END WHILE
为VCC中的所有节点设置替代节点,生成新的社团结构代表节点集合V′C。如算法1所示,VCC中的任一节点vi,其替代节点的设置可分为2步:
1) 如果节点vi的邻居节点vj属于社团结构代表点集合V′CA,则把节点vj设置为节点vi的替代节点。
2) 如果节点vj不是社团结构代表节点,则将节点vj的所有邻居节点添加到访问列表中,遍历查找直到找到节点vi的替代节点。
在对所有社团中的所有边缘节点进行压缩处理后,首先,合并所有新的社团结构代表点集合构建新的网络节点集V′;然后,遍历原始网络中的所有连边,把连边的端点用替代节点替换,删除重复边,得到压缩网络G′=(V′, E′);最后,采用经典的FR算法布局压缩网络中的节点,实现网络可视化压缩布局。
3 实验结果与分析本文选择网络社团分析领域3组标准数据集:dolphin、football及karat。其中,dolphin为海豚社会网络,football为美国大学生足球联赛社会网络,karat为美国空手道俱乐部社会网络。对应网络的节点数和连边数如表 1所示。
| 数据集 | 方法 | 节点数 | 连边数 | 平均聚类系数 | 社团数 |
| dolphin | 压缩前 | 62 | 159 | 0.303 | 5 |
| 方法1 | 12 | 29 | 0.716 | 3 | |
| 方法2 | 12 | 29 | 0.716 | 3 | |
| 本文方法 | 13 | 33 | 0.674 | 5 | |
| football | 压缩前 | 115 | 613 | 0.403 | 10 |
| 方法1 | 23 | 100 | 0.515 | 9 | |
| 方法2 | 23 | 96 | 0.570 | 8 | |
| 本文方法 | 26 | 97 | 0.534 | 10 | |
| karat | 压缩前 | 34 | 78 | 0.588 | 4 |
| 方法1 | 7 | 17 | 0.867 | 3 | |
| 方法2 | 7 | 17 | 0.867 | 3 | |
| 本文方法 | 8 | 18 | 0.733 | 4 |
将本文方法的压缩布局结果分别与基于节点度值(方法1)、PageRank(方法2)排序的网络压缩布局方法进行对比。首先,通过节点数、连边数、平均聚类系数和社团数等指标的变化定量评估不同压缩方法的压缩效果;然后,通过对压缩前后拓扑结构的可视化布局效果对比,定性分析本文方法的优势。其中,节点数和连边数的变化量表示网络的压缩规模;平均聚类系数的变化描述了网络中节点间连接关系的紧密程度,平均聚类系数越大,节点连接关系越紧密;社团数的变化反映了压缩网络是否保留了原始网络的社团构成。
实验中选择的节点压缩比为0.2,即方法1和方法2按照全网节点总数的20%筛选网络代表节点,本文方法按照每个社团中节点总数的20%筛选社团结构代表节点。
表 1为不同方法的压缩结果对比。可知,不同压缩方法通过合并非重要节点,较大程度地降低了节点和连边数量,实现了网络压缩的目的。
另外,压缩网络的平均聚类系数较压缩前有较大程度的升高,也表明了上述3种压缩方法都保留联系比较紧密的重要节点,这些节点及其之间的连边反映了网络的骨架结构。其中,基于节点度值(方法1)、PageRank(方法2)排序的压缩网络的平均聚类系数相对接近,且都大于本文方法。这是因为前2种方法虽然采用的节点重要性评估模型不同,节点重要性排序结果并不一样,但对于整体网络而言,重要节点都分布在排名靠前的区域。因此,基于网络全局节点重要性的压缩获得了相同或基本相同的代表节点集合。而本文方法对不同社团结构中的节点重要性分别排序,保留的节点是各个社团结构中的重要节点,代表了各社团的内部结构。虽然本文方法中压缩网络的平均聚类系数相对较低,但是社团数量没有减少,比较完整地保留了网络的社团构成,从中尺度上保留了网络的整体结构。而前2种方法都丢失了部分社团,造成网络整体结构的不完整。
图 3~图 5为分别采用上述3种方法对不同网络进行可视化压缩布局前后的效果图。将不同方法的布局效果进行对比,可以看出本文方法的优势主要体现在以下2个方面:

|
| 图 3 dolphin网络压缩前后布局效果 Fig. 3 Layout effect of dolphin network before and after compression |
|
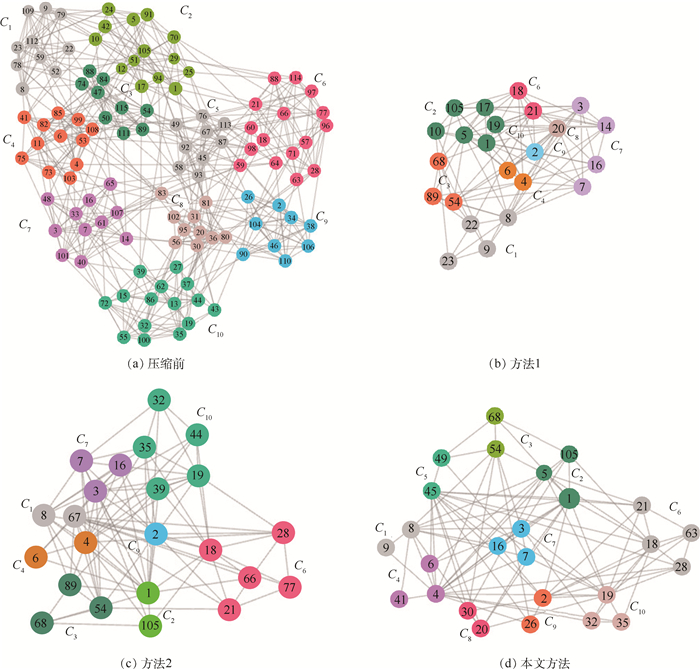
| 图 4 football网络压缩前后布局效果 Fig. 4 Layout effect of football network before and after compression |

|
| 图 5 采用本文方法对karat网络进行多粒度压缩前后布局效果 Fig. 5 Layout effect of karat network before and after multi-granularity compression by proposed method |
1) 基于社团结构进行压缩,能够保留网络的社团构成,突出中观尺度结构特征。
图 3(b)、(c)、(d)分别为方法1、方法2和本文方法的dolphin压缩网络的布局结果,图 4(b)、(c)、(d)分别为方法1、方法2和本文方法的foot-ball压缩网络的布局结果。与图 3(a)和图 4(a)中的原始网络布局结果对比,图 3(b)、(c)、(d)和图 4(b)、(c)、(d)中的节点数和连边数都有较大程度的压缩。图 3(a)和图 4(a)中的原始网络受屏幕尺寸限制,节点较小,连边密集,节点和连边重叠交叉现象严重。在混乱重叠的视图中,用户难以感知网络的整体结构。而上述3种方法通过缩减节点和连边规模,可以降低节点和连边重叠覆盖造成的视觉杂乱。但是,由于方法1(图 3(b)和图 4(b))和方法2(图 3(c)和图 4(c))基于全局结构评估节点的重要性和选择网络代表节点,对节点数量较少或者连边相对稀疏的社团没有保留有效的代表节点。在压缩过程中,这部分社团被压缩合并,造成社团数量减少,无法准确展示原始网络的社团构成。而本文方法(图 3(d)和图 4(d))基于社团结构进行压缩,保证每个社团结构都有代表节点,避免压缩过程中的社团丢失现象,能够反映网络在社团尺度(中观尺度)上的结构特征。
另外,基于社团结构的压缩更有助于感知网络整体结构和社团间的相互作用。以图 3(d)为例,可以发现,原始网络可划分为5个社团。其中,社团C1、C5包含节点数量较多,其他3个社团节点数量较少;社团C1、C5间的交互主要通过C2、C3这2个社团实现。C2、C3社团中的节点虽少,但是承担着全网节点交互的“桥梁”作用,对网络的拓扑构成十分重要。而图 3(b)、(c)中没有保留C2、C3社团,不能准确反映C2、C3社团的“桥梁”作用,C4直接与C1交互,容易对用户理解网络在中观尺度上的结构特征造成偏差。
2) 采用多粒度社团结构划分算法,展示社团基本结构,并实现网络的多粒度压缩布局。
本文方法在压缩边缘节点的同时保留了必要的社团结构代表节点。由于基于拓扑势对节点的重要性进行分析,保留的节点对社团构成的贡献较大,反映了社团的基本结构。通过保留这部分节点及连接关系,可以清晰地展示社团内部基本结构。同时,通过压缩非重要节点和删除重复连边,降低社团内部连边数量,有助于在视觉上感知社团结构,发现社团或网络结构中的重要节点。
根据社团结构划分的粒度,本文方法通过压缩合并边缘节点,有效降低网络规模、节点数和连边数,实现多粒度的压缩布局。图 5为对karat网络数据进行3级压缩布局的效果图。如图 5(d)所示,根据节点压缩比例的不同可以控制网络压缩比例,最多可将一个社团压缩为1个节点。如图 5(d)中每个节点代表一个社团,“节点”1、32、34之间能够直接交互,而“节点”6只能通过“节点”1与其他“节点”交互。
4 结论为有效展示网络的中尺度结构特征,将力导引布局算法与网络社团结构特征相结合,提出了一种基于社团结构节点重要性的网络可视化压缩布局方法。实验结果和分析表明,该方法的优势体现在3个方面:
1) 有效压缩节点和连边数量,降低视觉杂乱现象。
2) 比较完整地从中观尺度反映网络的结构构成与交互,便于分析不同社团或节点在网络拓扑中的不同作用。
3) 基于多粒度的社团结构探测和不同的节点压缩比可以实现多粒度的压缩展示。本文方法主要通过将网络压缩方法和力导引布局算法结合,从社团构成和社团结构上展示了网络的中观尺度结构,下一步将考虑与其他节点布局算法和交互方法结合,进一步优化布局结果。
| [1] |
张喜涛, 吴玲达, 于少波. 面向多层网络可视化的多力导引节点自动布局算法[J]. 计算机辅助设计与图形学学报, 2019, 31(4): 639-646. ZHANG X T, WU L D, YU S B. A multi-force directed layout algorithm for multilayer networks visualization[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(4): 639-646. (in Chinese) |
| [2] |
姚中华, 吴玲达, 宋汉辰. 网络图中边集束优化问题[J]. 北京航空航天大学学报, 2015, 41(5): 871-878. YAO Z H, WU L D, SONG H C. Problems of network simplification by edge bundling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 871-878. (in Chinese) |
| [3] |
LESKOVEC J, FALOUTSOS C.Sampling from large graphs[C]//Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2006: 631-636.
|
| [4] |
杜晓林.大规模社会网络可视化若干问题及算法研究[D].哈尔滨: 哈尔滨工业大学, 2015: 18-35. DU X L.Research on visualization problems and algorithms for large scale social network[D].Harbin: Harbin Institute of Technology, 2015: 18-35(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957412.htm |
| [5] |
GILBERT A C, LEVCHENKO K.Compressing network graphs[C]//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2004: 1-10.
|
| [6] |
ALMENDRAL J A, CRIADO R, LEYVA I, et al. Introduction to focus issue:Mesoscales in complex networks[J]. Chaos, 2011, 21(1): 016101. DOI:10.1063/1.3570920 |
| [7] |
EADES P. A heuristic for graph drawing[J]. Congressus Numerantium, 1984, 42: 149-160. |
| [8] |
KAMADA T, KAWAI S. An algorithm for drawing general undirected graphs[J]. Information Processing Letters, 1989, 31(1): 7-15. |
| [9] |
DAVIDSON R, HAREL D. Drawing graphs nicely using simulated annealing[J]. ACM Transactions on Graphics, 1996, 15(4): 301-331. DOI:10.1145/234535.234538 |
| [10] |
FRUCHTERMAN T M J, REINGOLD E M. Graph drawing by force-directed placement[J]. Software-Practice and Experience, 1991, 21(11): 1129-1164. DOI:10.1002/spe.4380211102 |
| [11] |
水超, 陈洪辉, 陈涛, 等. 力导向模型的复杂网络社区挖掘算法[J]. 国防科技大学学报, 2014, 36(4): 163-168. SHUI C, CHEN H H, CHEN T, et al. A community detect algorithm on force-directed model[J]. Journal of National University of Defense Technology, 2014, 36(4): 163-168. (in Chinese) |
| [12] |
ZHANG X T, WU L D, YU S B. Layer-edge patterns exploration and presentation in multiplex networks:From detail to overview via selections and aggregations[J]. Electronics, 2019, 8(4): 387. DOI:10.3390/electronics8040387 |
| [13] |
王晓华, 杨新艳, 焦李成. 基于多尺度几何分析的复杂网络压缩策略[J]. 电子与信息学报, 2009, 31(4): 968-972. WANG X H, YANG X Y, JIAO L C. Compression of complex networks based on multiscale geometric analysis[J]. Journal of Electronics & Information Technology, 2009, 31(4): 968-972. (in Chinese) |
| [14] |
李甜甜, 卢罡, 许南山, 等. 基于k-core的大规模复杂网络压缩布局算法[J]. 计算机工程, 2016, 42(5): 308-312. LI T T, LU G, XU N S, et al. Compressing layout algorithm for large complex network based on k-core[J]. Computer Engineering, 2016, 42(5): 308-312. DOI:10.3969/j.issn.1000-3428.2016.05.054 (in Chinese) |
| [15] |
肖俐平, 孟晖, 李德毅. 基于拓扑势的网络节点重要性排序及评价方法[J]. 武汉大学学报(信息科学版), 2008, 33(4): 379-383. XIAO L P, MENG H, LI D Y. Approach to node ranking in a netwrok based on topology potential[J]. Geomatics and Information Science of Wunan University, 2008, 33(4): 379-383. (in Chinese) |
| [16] |
王戬.一种基于拓扑势的社会网络节点重要性评估方法[D].哈尔滨: 哈尔滨工程大学, 2015: 18-30. WANG J.Evaluating the importance of nodes in social networks based on topology potential[D].Harbin: Harbin Engineering University, 2015: 18-30(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10217-1018047823.htm |
| [17] |
GACH O, HAO J K.Improving the Louvain algorithm for community detection with modularity maximization[C]//International Conference on Artificial Evolution (Evolution Artificielle).Berlin: Springer, 2013: 145-156.
|



