2. 江苏省食品先进制造装备技术重点实验室, 无锡 214122;
3. 苏州工业职业技术学院, 苏州 215104
2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China;
3. Suzhou Vocational Institute of Industrial Technology, Suzhou 215104, China
传统机器人多以刚性结构为主,其结构复杂、自适应能力差、自由度有限、安全性低[1-3]。与刚性机器人不同,软体机器人基于仿生学的研究成果[4-6],以新兴的智能材料为依托[7],模仿自然界中的无脊椎动物,如蚯蚓、章鱼及动物的舌等。其结构一般比较简单、自适应能力强、理论上可以有任意自由度、安全性较高[8]。因此,软体机器人可在医疗手术、地震救援、故障检测[9-10]等诸多非结构化工作环境中完成既定任务。
基于软体机器人的诸多优良特性以及其在非结构化工作环境中的广阔应用前景,其正逐渐成为国内外机器人领域的研究热点。综合国内外软体机器人的发展历程不难发现,基于驱动方式软体机器人可划分为:气动驱动[11-12]、丝线驱动[13]以及智能材料电致动[14-16]。在气动驱动方面,Fionnuala等[17]用实验法总结了纤维增强型软体驱动器的变形规律;Kevin等[18]基于实验法分析了水下软体夹持器的力学特性;Kristin等[19]基于欧拉弹力定理和杆理论建立气动软体驱动器的理论模型;王宁扬等[20]基于形封闭性理论分析了蜂巢气动软体夹持器的变形机理;魏树军等[21]基于实验法研发了一种纤维增强型气动软体抓手;郑俊君等[22]基于流体静压力学特性构建了气动静压软体机器人的理论模型;王华等[23]在橡胶材料本构关系的基础上,应用虚功原理分析了软体弯曲驱动器的变形机理;费燕琼等[24]基于橡胶材料的本构关系,分析了气动驱动软体机器人的运动机理。在丝线驱动方面,Kim等[25]基于欧拉-伯努利梁方程构建了SMA(Shape Memory Alloys)丝驱动的软体手的理论模型;Mathijssen等[26]基于等距实验法总结了人工肌肉丝驱动器的变形规律;史震云和朱前成[27]基于径向基函数神经网络和支持度函数构建了智能驱动器软体机器人的理论模型;王扬威等[28]基于运动学模型分析了形状记忆合金丝驱动柔性机械臂的变形机理;Fei和Xu[29]基于实验法及反馈数据总结了SMA软体驱动器的变化规律。在电致动方面,Matlu等[30]基于静准态有限元模型分析了EAP(Electro Active Polymer)致动装置的变形机理;郭闯强等[16]基于IPMC(Ionic Polymer Metal Composote)分析了微型仿生机器鱼鱼的变形机理。
在食品科学领域,模拟咀嚼、吞咽功能的软体仿生舌的研制具有重要价值,谢高鹏提出了仿生舌并进行了食品咀嚼模拟机系统的研究[31];韩敬虎[32]设计了一款仿生舌并研制了咀嚼吞咽一体化仿生机器人。
本文以软体仿生舌为研究对象,研究了驱动器的变形机理,并基于Yeoh模型建立了非线性数学模型,开展了软体仿生舌的仿真研究及相关实验验证,结果证明了结构设计的合理性以及理论模型的正确性。
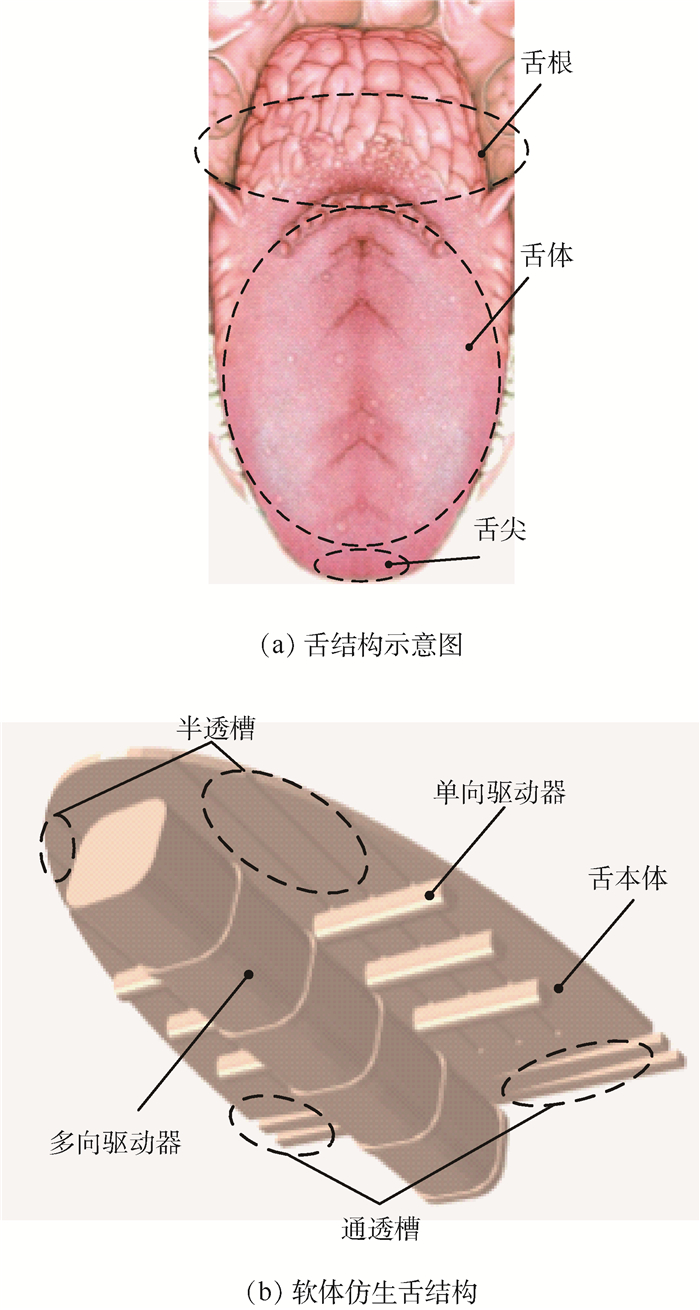
1 软体仿生舌的结构设计如图 1(a)所示,舌是口腔内的肌性器官,可分为舌根、舌体和舌尖三部分。作为一种骨骼肌,其运动十分灵活,参与咀嚼、吞咽及协助语言等功能。
|
| 图 1 舌示意图 Fig. 1 Diagram of tongue |
为模拟舌的吞咽、咀嚼等功能,基于气动驱动器设计了一款软体仿生舌,如图 1(b)所示。该软体仿生舌主要由多向驱动器、单向驱动器及舌本体组成,其中单/多向驱动器黏附在舌本体下部,控制仿生舌的吐舌、翻舌、卷舌及斜翻舌等功能,同时半/通透槽可减少挤压应力,在驱动压强p=50 kPa时,预期吐舌5 mm,翻舌1.2 rad,卷舌1.3 rad,斜翻舌1 rad。
软体仿生舌制备材料均为肖氏硬度20度的硅橡胶,具体方法为模具浇铸法,基于3D打印得到树脂模具,配合1:1混合的液态硅胶固化完成制备工序。
1.1 多向驱动器结构及工作原理多向驱动器由4个充气软管通过实心连接管连接而成,其外部包覆有约束管和约束线圈,如图 2所示。当对其中一个充气软管充气时,在气压p的作用下软管膨胀并轴向拉伸,同时受驱动器中非受压软管的应力σ、外部约束管及约束线圈约束作用,从而整个驱动器完成弯曲动作。同理,若对其他充气软管充气驱动器就会完成其相应方向的弯曲动作;如对2个软管进行充气,则会完成较之前偏转45°的弯曲动作,图 2中R为弯曲半径,L0为驱动器原长;若对所有充气软管充气驱动器则会完成拉伸动作。

|
| 图 2 多向驱动器结构及工作原理图 Fig. 2 Diagram of structure and working principle of multi-directional actuator |
该软体仿生舌尺寸以成年男性舌的大小为设计依据,并以1:1确定各结构尺寸,多向驱动器结构参数如表 1所示。
| 参数 | 数值/mm |
| 驱动器长度L | 100 |
| 连接管半径r0 | 1.66 |
| 充气软管内径r1 | 3 |
| 充气软管外径r2 | 4 |
| 约束管圆弧半径r3 | 5 |
| 约束管薄板宽a | 1 |
| 约束管薄板长b | 8 |
1.2 单向驱动器结构及工作原理
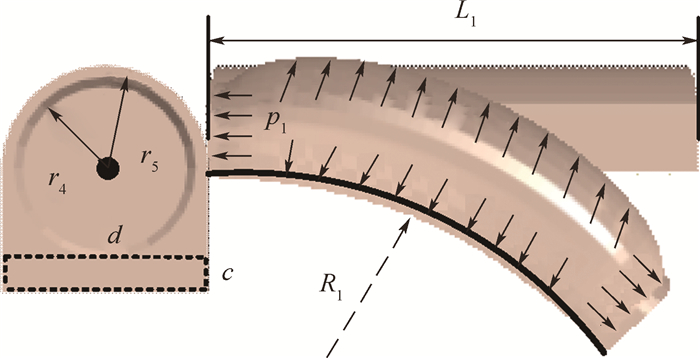
单向驱动器主要由充气软管和底部较厚的硅橡胶板组成,两者紧密粘合在一起,如图 3所示。当对软管充气时,在气压p1的作用下软管膨胀并轴向拉伸,同时驱动器中非受压软管的应力σ1则起到限制作用,从而单向驱动器实现弯曲功能,其弯曲半径R1如图 3所示。
|
| 图 3 单向驱动器结构及工作原理图 Fig. 3 Diagram of structure and working principle of one-directional actuator |
同理,基于软体仿生舌结构尺寸参数,可确定单向驱动器结构参数,具体如表 2所示。
| 参数 | 数值/mm |
| 驱动器长度L1 | 100 |
| 充气软管内径r4 | 2.2 |
| 充气软管外径r5 | 2.5 |
| 约束管薄板宽c | 0.8 |
| 约束管薄板长d | 5 |
2 驱动器变形机理的理论建模
单/多向驱动器变形机理的研究是软体仿生舌运动特性研究的理论基础,因此有必要构建单/多向驱动器变形机理的理论模型。值得指出的是,硅橡胶作为超弹性材料,一般具有各向同性和不可压缩性[31],且各项力学特性均表现为非线性,因此本文首先研究较为基础的运动特性。
2.1 硅橡胶材料的应变能密度函数对超弹性材料非线性力学的研究,其常用的研究方法有以下几种:非线性方程的线性化;最小势能原理;应变能密度函数等。线性化是通过Piola-Kirchhoff应力和Cauchy-Green应变建立Lagrange方程[32],将非线性方程线性化进行求解;此类方法求解相对简单,但是不易得到精确解,故应用不是很广泛。最小势能原理是根据能量法建立平衡方程[23]。应变能法是基于弹性力学并选择合适的应变能密度函数来建立力的平衡方程[24]。
该软体驱动器结构简单,变形较大且变形后软管处于非确定性状态,因此Lagrange方程和能量方程不易构建。同时,文献[33]表明Yeoh模型应变能密度函数能适用于超弹性材料的大变形行为,因此,本文拟采用应变能密度函数对驱动器的变形机理进行研究。
首先根据应力应变关系以唯象理论建立硅橡胶材料的本构关系[33],并采用应变能密度函数进行表示:
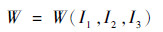
|
(1) |
式中:
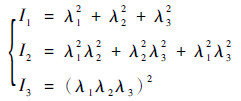
|
(2) |
其中:I1, 2, 3为变形张量不变量;λ1, 2, 3为拉伸比,假设硅橡胶材料是不可压缩的,可得
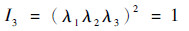
|
(3) |
常用的应变能密度函数模型有Neo-Hookean模型、Yeoh模型、Mooney-Rivlin模型等,其中Yeoh模型常用来描述大变形行为[34],故本文拟采用其最经典的二参数形式:
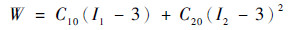
|
(4) |
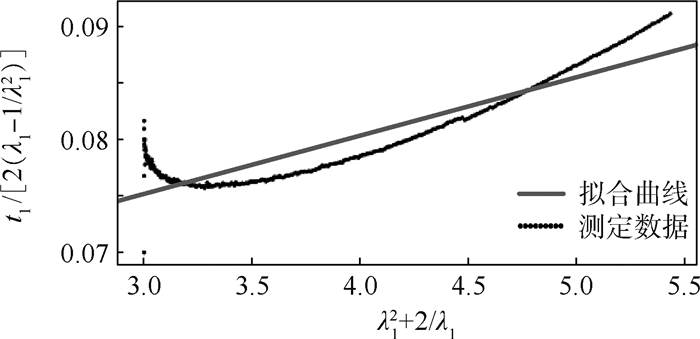
式中:C10、C20为硅橡胶材料的Yeoh模型材料常系数,如图 4所示。其可利用CTM2100微机控制电子拉伸仪通过单轴向拉伸实验测定,限于篇幅,具体测定过程不予赘述。
|
| 图 4 Yeoh模型材料常数拟合曲线 Fig. 4 Fitting curve of Yeoh model parameter |
依据[33]文献中“求Yeoh模型常数部分”,可得到公式t1/[2(λ1-1/λ12)]=2C20(λ12+2/λ1)+C10-6C20,测得拉伸比λ1和主应力t1,将t1/[2(λ1-1/λ12)]作为y轴,λ12+2/λ1作为x轴,可以拟合并计算出材料常系数C10=0.072,C20=0.002 5。
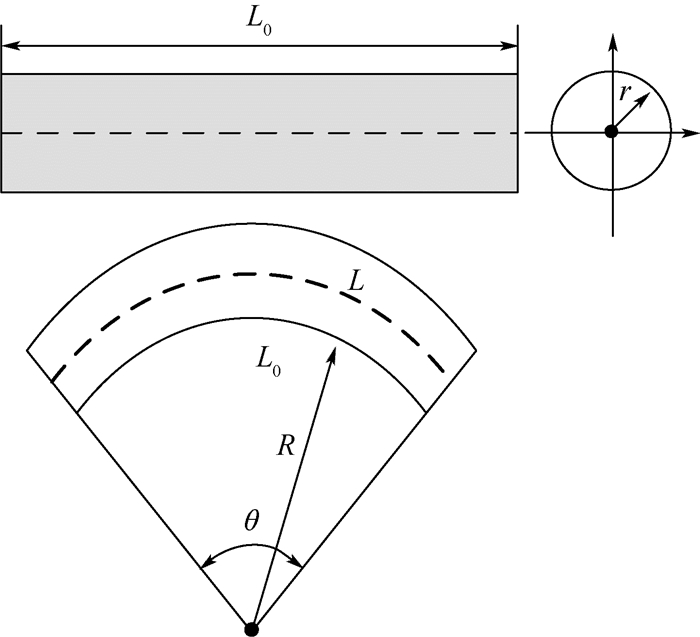
2.2 驱动器弯曲变形理论模型分析多向驱动器的结构发现,整个驱动器由实心连接管、充气软管以及约束薄板组成。而实心连接管与充气软管只在截面积上存在差异,故可以归结为一类,如图 5所示。为分析其变形机理,假设驱动器原长为L0,变形后为L,变形后的曲率半径和弧长分别为R和θ,根据硅橡胶材料的不可压缩性,可认为底部长度无变化,仍为L0。
|
| 图 5 管状弯曲状态示意图 Fig. 5 Bending diagram of tube |
基于Yeoh模型应变能密度函数,该驱动器在弯曲变形过程中,长度方向上的拉伸最为明显,设定为λ1,而其余2个方向拉伸比相同,结合式(3)可得

|
(5) |
根据图 5并结合弧长和半径的几何关系可以得到

|
(6) |
基于式(2)和式(5)可得

|
(7) |
基于应力与应变能关系:
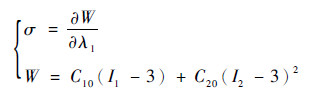
|
(8) |
联立式(7)和式(8)可确定约束管应力大小:
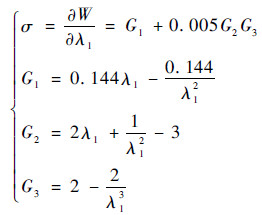
|
(9) |
约束薄板的弯曲状态与圆管类似,但截面形状的不同导致其拉伸比不同。其在整个弯曲变形过程当中,长度方向上的拉伸最为明显,设定为λ1,宽度方向的拉伸比仅存在很微小的变化[16],假设厚度方向拉伸比不变(λ3=1),则结合式(3)可得
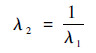
|
(10) |
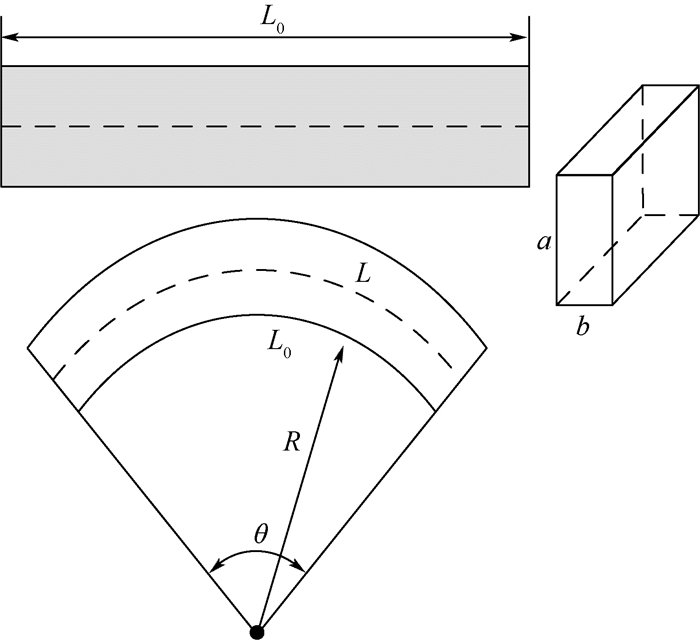
根据图 6并进一步考虑弧长和半径的几何关系可以得到
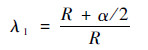
|
(11) |
|
| 图 6 板状弯曲状态示意图 Fig. 6 Bending diagram of board |
同理,基于式(2)和式(10)可以得到
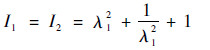
|
(12) |
联立式(12)和式(8)可确定约束薄板应力大小:

|
(13) |
必须指出的是,在受到驱动压强的作用后,驱动器在径向的拉伸会导致轴向的横截面积发生变化,本文采用次拉伸比(λ2, λ3)来表征变形后的横截面积,即S=S0λ2λ3,其中S0为原横截面积的大小,S为变形后横截面积的大小。
根据图 2的受力示意图,构建其力平衡方程:
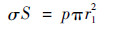
|
(14) |
联立式(6)、式(9)和式(14)可进一步推导求得驱动器弯曲半径R与驱动压强p的函数表达式,限于篇幅,不予赘述,其可表示为
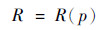
|
(15) |
同理,结合上述单向驱动器结构发现,其包括充气软管和约束薄板,其变形机理可联立式(11)、式(13)和式(14),推导求得驱动器弯曲半径R1与输入压强p1的函数表达式,其可表示为
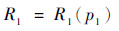
|
(16) |
式(15)表征了不同驱动压强作用下,多向驱动器的弯曲变形后的曲率半径,而式(16)表征了不同驱动压强作用下单向驱动器的弯曲半径,上述为后续软体仿生舌的控制奠定了理论基础。
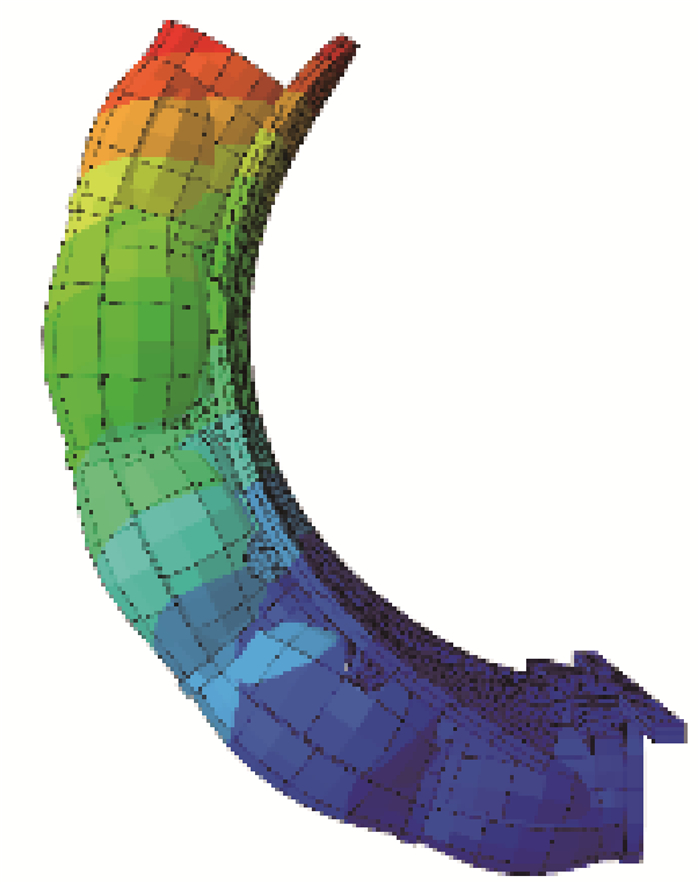
3 软体仿生舌有限元仿真为验证上述理论模型的正确性,并更加直观形象地表征单/多向驱动器在气动驱动下的弯曲变形过程,如图 7所示,基于Abaqus软件对驱动器进行有限元仿真。
|
| 图 7 软体仿生舌仿真示意图 Fig. 7 Simulation diagram of soft bionic tongue |
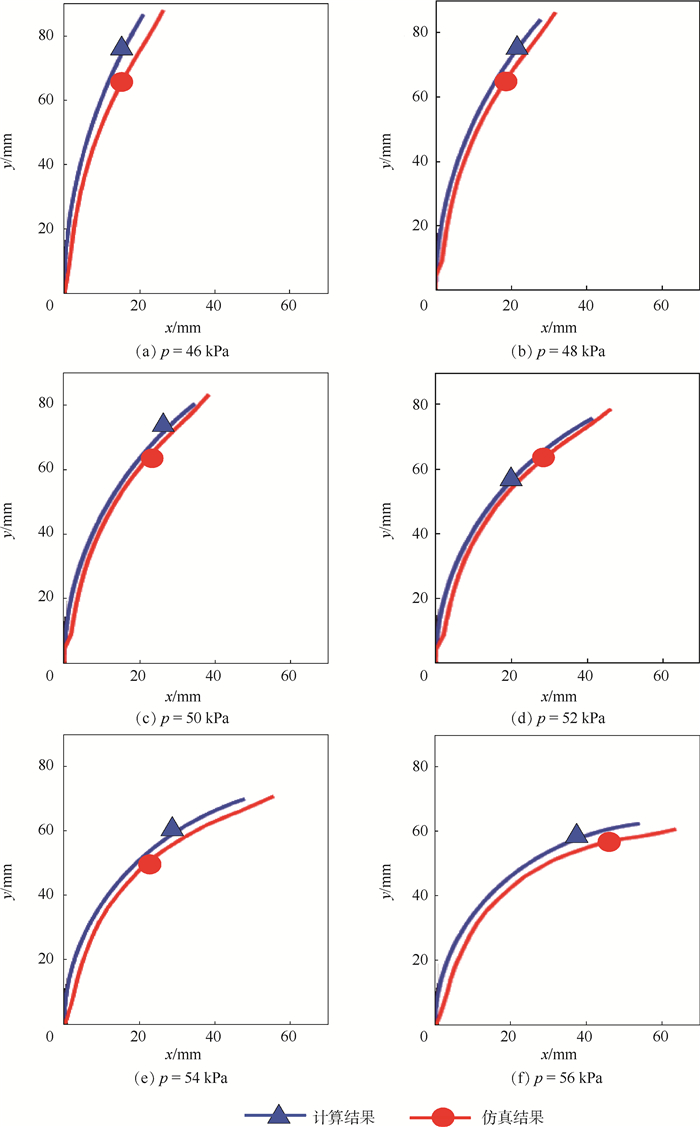
基于上文所述,由于多向驱动器由软管对称连接而成,故以单个软管充气为例,图 8给出了不同驱动压强作用下多向驱动器弯曲变形的理论计算值及有限元仿真值。
|
| 图 8 多向驱动器的弯曲变形理论计算值及有限元仿真值 Fig. 8 Theoretical calculations and finite element simulations with bending deformation of multi-directional actuator |
为了更加清楚地表征多向驱动器的变化规律,表 3展示了不同驱动压强作用下其末端点坐标的计算及仿真结果。
| p/kPa | xF/mm | yF/mm | xJ/mm | yJ/mm | 相对误差/% |
| 46 | 26.296 | 87.974 | 20.920 | 86.671 | 5.71 |
| 48 | 31.726 | 86.194 | 27.761 | 84.011 | 7.21 |
| 50 | 38.361 | 83.271 | 34.809 | 80.289 | 8.89 |
| 52 | 46.248 | 78.535 | 41.7575 | 75.426 | 7.65 |
| 54 | 55.470 | 70.747 | 48.307 | 69.396 | 9.63 |
| 56 | 63.735 | 60.534 | 54.0700 | 62.363 | 10.52 |
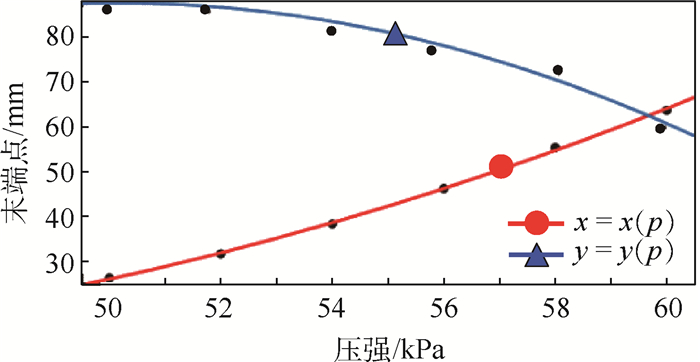
值得指出的是,上述数据只能表征固定驱动压强作用下多向驱动器末端点的位置坐标,为从一般意义上来表征其末端点随压强的变化关系,如图 9所示,可将计算结果的各坐标点进行轨迹拟合,拟合结果如下:
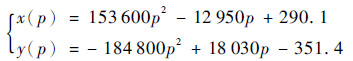
|
(17) |
|
| 图 9 多向驱动器末端点坐标拟合曲线 Fig. 9 Fitting curves with coordinate points of multi-directional actuator |
1) 多向驱动器末端坐标点的理论计算值与有限元仿真值基本一致,从而验证了理论模型的正确性。
2) 随着驱动压强p的增大,多向驱动器末端点坐标点的理论计算与有限元仿真的相对误差不断增大,其原因在于硅橡胶材料在大应变时表现出高度的非线性特性特性。
3) 基于末端点坐标的相对误差可以发现,当驱动压强大于56 kPa后,其相对误差逐渐增大并超过10%,故该软体仿生舌的工作压强在56 kPa以内。
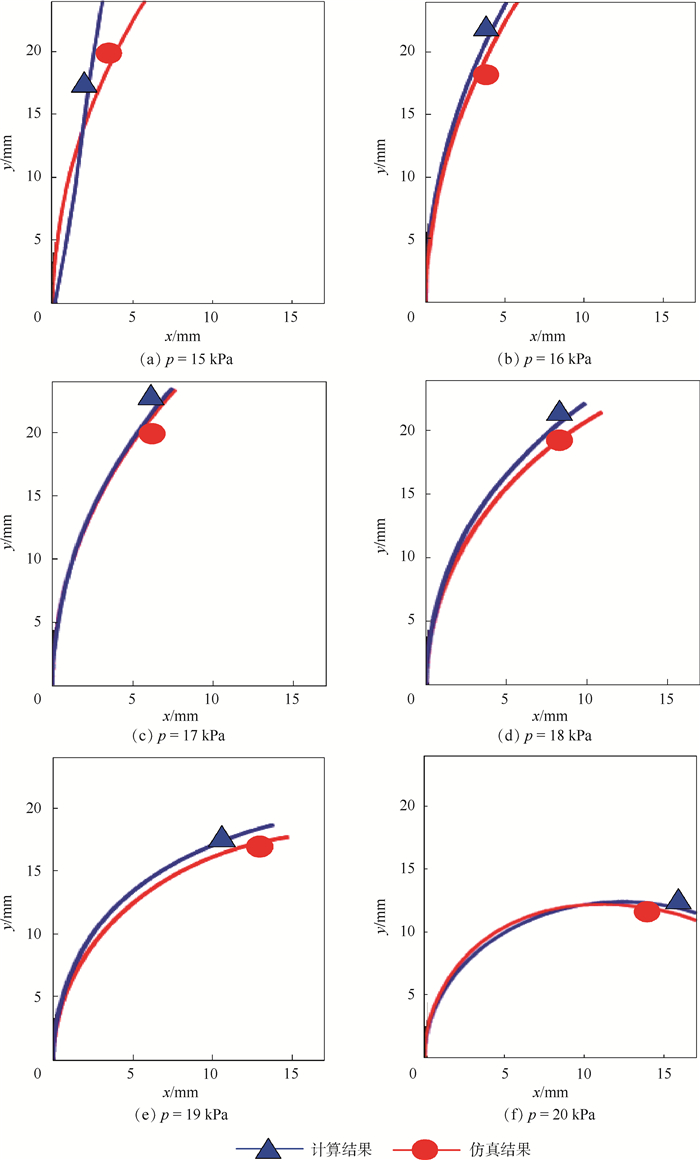
3.2 单向驱动器弯曲变形同理,以单向驱动器为研究对象,图 10给出了不同驱动压强作用下单向驱动器弯曲变形的理论计算值及有限元仿真值。
|
| 图 10 单向驱动器的弯曲变形理论计算值及有限元仿真值 Fig. 10 Theoretical calculations and finite element simulations with bending deformation of one-directional actuator |
同理,为了更加清楚地表征单向驱动器的弯曲状况,表 4展示了不同驱动压强作用下其弯曲变形所对应圆心角的理论计算值、有限元仿真值及相对误差。
| p/kPa | θF/rad | θJ/rad | 相对误差/% |
| 15 | 0.395348 | 0.421403 | 6.59041 |
| 16 | 0.423527 | 0.448456 | 5.886147 |
| 17 | 0.632721 | 0.602154 | 4.831062 |
| 18 | 0.939089 | 0.852957 | 9.171863 |
| 19 | 1.383204 | 1.35569 | 1.989166 |
| 20 | 2.018431 | 2.198672 | 8.929779 |
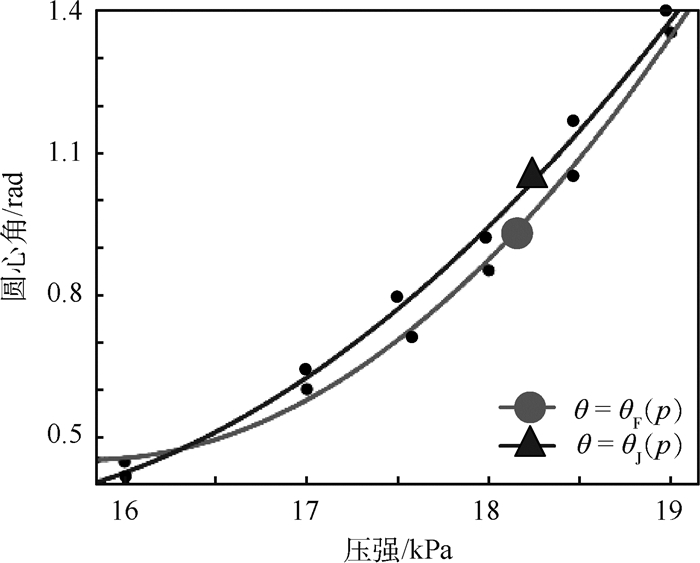
同理,值得指出的是,上述数据也只能表征固定驱动压强作用下单向驱动器的弯曲状态,为从一般意义上来表征其圆心角随压强的变化关系,如图 11所示,可将结果进行轨迹拟合,拟合结果为
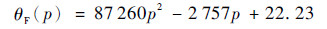
|
(18) |
|
| 图 11 单向驱动器弯曲圆心角拟合曲线 Fig. 11 Fitting curves with bending center angle of one-directional actuator |
基于仿真结果,单向驱动器弯曲圆心角的有限元仿真值与实验值相对误差基本不超过10%;单向驱动器带动仿生舌可完成2 rad运动,符合预期1.3 rad的目标。上述分析证明了单向驱动器弯曲变形理论模型的正确性。
4 实验验证为进一步验证理论模型与有限元仿真的正确性,本文开展了软体仿生舌运动特性的实验研究,实验平台如图 12所示。小型隔膜泵(DC12 V)由软管分别连接软体驱动器和Y100气压表(100 kPa),电源(DC12V3A)连接直流电机调速板(DC5-18V)控制气泵的输出压强。实验过程中主要考虑驱动器在平面内的弯曲运动,故驱动器充气端固定,而运动端进行数据采集,并由坐标纸得到相关实验数据。

|
| 图 12 软体仿生舌运动特性实验平台 Fig. 12 Experiment platform with motion characteristics of soft bionic tongue |
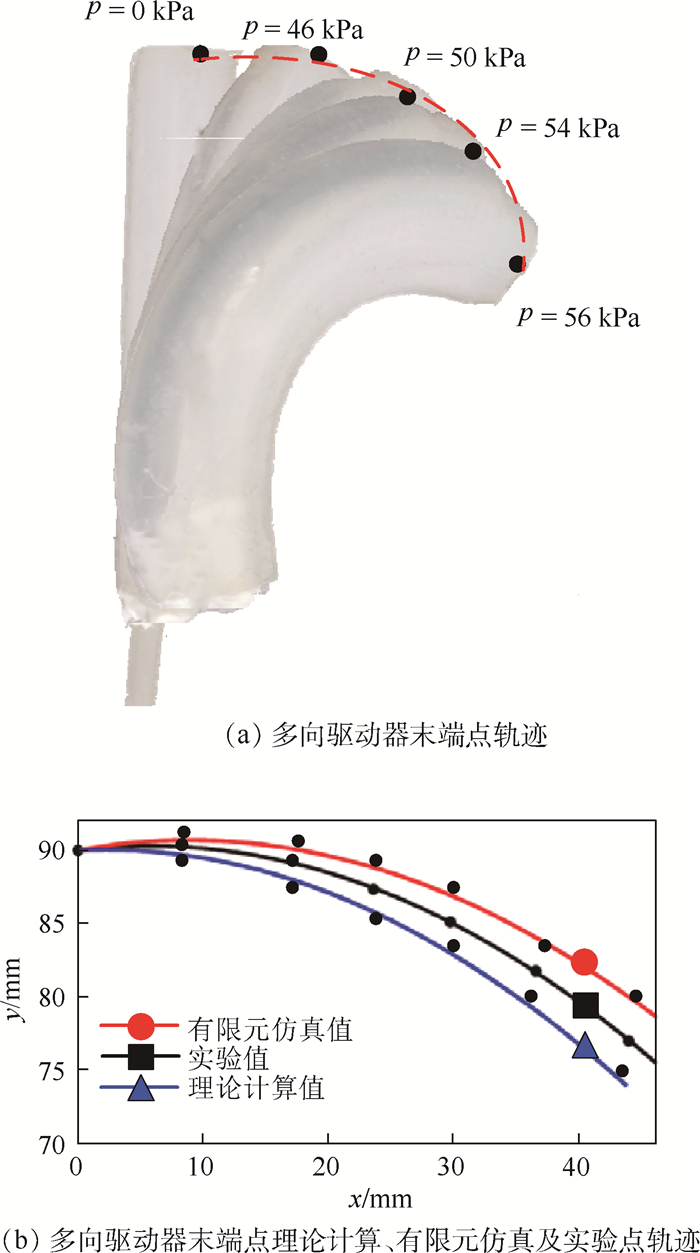
基于上述实验平台,图 13(a)展示了不同驱动压强作用下多向驱动器的弯曲变形状态。联立表 3,多向驱动器在不同驱动压强作用下末端点坐标的有限元仿真值、实验值和理论计算值如图 13(b)所示。
|
| 图 13 多向驱动器弯曲实验结果 Fig. 13 Bending experiment result of multis-directional actuator |
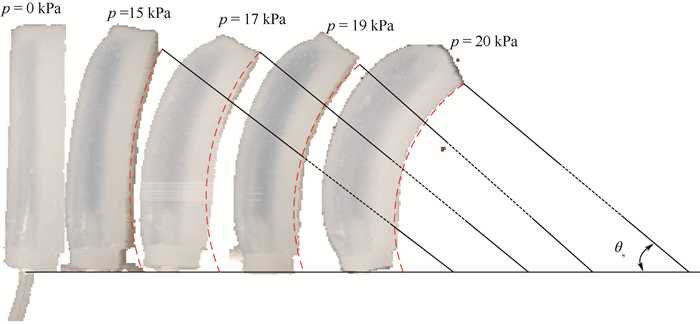
同理,图 14展示了不同驱动压强作用下单向驱动器的弯曲状态,其理论计算、有限元仿真及实验结果如表 5所示。
|
| 图 14 单向驱动器弯曲圆心角 Fig. 14 Bending center angle of one-directional actuator |
| p/kPa | θJ/rad | θF/rad | θS/rad |
| 15 | 0.382480028 | 0.4214032 | 0.4 |
| 16 | 0.416491474 | 0.448456 | 0.4 |
| 17 | 0.515337908 | 0.602154 | 0.5 |
| 18 | 0.773391507 | 0.852957 | 0.7 |
| 19 | 1.241311947 | 1.35569 | 1.2 |
| 20 | 2.411736242 | 2.198672 | 1.9 |
4.2 软体仿生舌运动
为验证软体仿生舌的助咀嚼、助吞咽功能,可进行软体仿生舌的翻舌、斜翻舌、吐舌及卷舌动作实验,图 15(a)和图 15(b)分别展示了仿真与实验结果。实验仍采用上述实验平台,其中,对多向驱动器下面(图示位置)2个软管充气完成翻舌运动;对单个软管充气完成仿生舌斜上拉运动;对4个软管同时充气则可以完成吐舌动作。

|
| 图 15 软体仿生舌实验 Fig. 15 Experiment of soft bionic tongue |
同理,改变2个软管充气的位置则可以实现软体仿生舌左右摆动及翻舌运动;改变单个软管的充气位置则可以实现不同方向的斜翻舌;进而,通过上述多种运动方式的组合,可以完成仿生舌的助咀嚼、助吞咽功能,表 6展示了p=50 kPa仿生舌各项的实验与仿真结果。
| 运动类型 | 实验结果 | 仿真结果 |
| 翻舌/rad | 1.4 | 1.520312 |
| 斜上翻/rad | 1.2 | 1.310291 |
| 斜下翻/rad | 1.1 | 1.253652 |
| 左摆舌/rad | 1.3 | 1.49212 |
| 右摆舌/rad | 1.3 | 1.49212 |
| 吐舌/mm | 6.4 | 5.93356 |
| 卷舌/mm | 1.2 | 1.426356 |
基于上述实验结果,软体仿生舌可基本实现翻舌、吐舌等各项运动,且均符合预期吐舌5 mm,翻舌1.2 rad、斜翻舌1 rad及卷舌1.3 rad的目标。上述分析进一步证明了软体仿生舌结构设计、指定运动的合理性及理论模型的正确性。
该软体仿生舌的柔软性与真实的舌具有高相似性,其可应用于模拟吞咽功能,对治疗吞咽困难症具有重要意义。为精准有效的对仿生舌进行控制,需搭建仿生舌的控制系统,目前基于Arduino控制系统的构建尚在进行之中。
5 结论1) 本文基于单/多向气动驱动器设计了一款软体仿生舌,该软体仿生舌可完成吐舌、翻舌、卷舌以及斜翻舌等动作。
2) 基于Yeoh模型应变能密度函数,结合力平衡方程,建立了单/多向气动驱动器的弯曲变形理论模型。进一步开展了气动驱动器的有限元仿真研究,验证了理论模型的正确性。
3) 开展了软体仿生舌的实验研究,验证了单/多向驱动器弯曲理论计算、仿真值与实验结果的一致性,也验证了软体仿生舌各运动的可行性。
| [1] |
曹玉君, 尚建忠, 梁科山, 等. 软体机器人研究现状综述[J]. 机械工程学报, 2012, 48(3): 25-33. CAO Y J, SHANG J Z, LIANG K S, et al. A review on the softrobotics[J]. Journal of Mechanical Engineering, 2012, 48(3): 25-33. (in Chinese) |
| [2] |
张忠强, 邹娇, 丁建宁, 等. 软体机器人驱动研究现状[J]. 机器人, 2018, 40(5): 648-659. ZHANG Z Q, ZOU J, DING J N, et al. Research status of the soft robot driving[J]. Robot, 2018, 40(5): 648-659. (in Chinese) |
| [3] |
RUS D, TOLLEY M T. Design fabrication and control of soft robots[J]. Nature, 2015, 521(7553): 467-475. DOI:10.1038/nature14543 |
| [4] |
谢哲新, 龚哲元, 王田苗, 等. 可控三维运动的软体驱动器仿真与试验[J]. 机械工程学报, 2018, 54(21): 460-468. XIE Z X, GONG Z Y, WANG T M, et al. Simulation and experiment sofa controllable soft spatial fluidic elastomer manipulator[J]. Journal of Mechanical Engineering, 2018, 54(21): 460-468. (in Chinese) |
| [5] |
苏满佳, 张逸鸿, 谢荣臻, 等. 连续软体机器人的结构范型与形态复现[J]. 机器人, 2018, 40(5): 640-647. SU M J, ZHANG Y H, XIE R Z, et al. Structural pattern and shape reproduction for soft continuum robot[J]. Robot, 2018, 40(5): 640-647. (in Chinese) |
| [6] |
樊继壮, 于庆国, 袁博文, 等. 软体仿蛙游动机器人关节式气动致动器研制[J]. 机器人, 2018, 40(5): 578-586. FAN J Z, YU Q G, YUAN B W, et al. Development of a joint-like pneumatic actuator applied to soft frog-inspired swimming robot[J]. Robot, 2018, 40(5): 578-586. (in Chinese) |
| [7] |
ILIEVSKI F, MAZZEO A D, SHEPHERD R F, et al. Soft robotics for chemists[J]. Angewandte Chemie, 2011, 50(8): 1890. DOI:10.1002/anie.201006464 |
| [8] |
胡兵兵, 金国庆. 一种仿虎甲幼虫的多驱动器软体机器人的设计与制造[J]. 机器人, 2018, 40(5): 626-633. HU B B, JIN G Q. Designand fabrication of a multi-actuator soft robot inspired by young tigerbeetle[J]. Robot, 2018, 40(5): 626-633. (in Chinese) |
| [9] |
DEIMEL R, BROCK O. A novel type of compliant and underactuated robotic hand for dexterous grasping[J]. International Journal of Robotics Research, 2015, 35(1): 161-185. |
| [10] |
TOLLEY M T, SHEPHERD R F, MOSADE B, et al. A resilientuntethered soft robot[J]. Soft Robotics, 2014, 1(3): 213-223. |
| [11] |
WEHN M, TRUBY R L, FITZGERALD D J, et al. An integrated design and fabrication strategy for entirely soft autonomous robots[J]. Nature, 2016, 536(7617): 451-455. DOI:10.1038/nature19100 |
| [12] |
BARTLETT N W, TOLLEY M T, OVERVELDE J T, et al. A 3D-printed functionally graded soft robot powered by combustion[J]. Science, 2015, 349(6244): 161-165. DOI:10.1126/science.aab0129 |
| [13] |
LASCHI C, CIANCHETTI M, MAZZOLAI B, et al. Soft robot arm inspired by the octopus[J]. Advanced Robotics, 2012, 26(7): 709-727. DOI:10.1163/156855312X626343 |
| [14] |
SHINTAKE J, ROSSET S, SCHUBERT B, et al. Versatile soft grippers with intrinsic electroadhesion based on multifunctional polymer actuators[J]. Advanced Materials, 2016, 28(2): 231-238. DOI:10.1002/adma.201504264 |
| [15] |
SHEN Q, TRABIA S, STALBAUM T, et al. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending twisting and oscillation[J]. Scientific Reports, 2016, 6(2): 24462. |
| [16] |
郭闯强, 吴春亚, 刘宏. 离子聚合物金属复合材料驱动器在机器人中的应用进展[J]. 机械工程学报, 2017, 53(9): 1-13. GUO C Q, WU C Y, LIU H. The application progress of ionicpolymer-metal composite materials in robotics[J]. Journal of Mechanical Engineering, 2017, 53(9): 1-13. (in Chinese) |
| [17] |
CONNOLL Y, FIONNUALA W, CONOR J B. Automatic design of fiber-reinforced soft actuators for trajectory matching[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(1): 51-56. DOI:10.1073/pnas.1615140114 |
| [18] |
KEVIN C G, KAITLYN P B, BRENNAN P. Soft robotic grippers for biological sampling on deep reefs[J]. Soft Robotics, 2016, 3(1): 2169-5172. |
| [19] |
KRISTIN M, OLIVER M, REILLY O. On constitutive relations for a rod-based model of a pneu-net bending actuator[J]. Extreme Mechanics Letters, 2016, 8(2): 38-46. |
| [20] |
王宁扬, 孙昊, 姜皓, 等. 一种基于蜂巢气动网络的软体夹持器抓取策略研究[J]. 机器人, 2016, 38(3): 371-384. WANG N Y, SUN H, JIANG H, et al. Study on grabbing algorithm of soft gripper based on honeycomb pneumatic network[J]. Robot, 2016, 38(3): 371-384. (in Chinese) |
| [21] |
魏树军, 王天宇, 谷国迎. 基于纤维增强型驱动器的气动软体抓手设计[J]. 机械工程学报, 2017, 53(13): 29-38. WEI S J, WANG T Y, GU G Y. Design of pneumatic soft grips based on fiber reinforced drivers[J]. Chinese Journal of Mechanical Engineering, 2017, 53(13): 29-38. (in Chinese) |
| [22] |
郑俊君, 宋小波, 姜祖辉. 一种气动静压软体机器人的驱动力产生机理及控制策略[J]. 机器人, 2014, 36(5): 513-518. ZHENG J J, SONG X B, JIANG Z H. The mechanism and control strategy of driving force of a pneumatic hydrostatic soft robot[J]. Robot, 2014, 36(5): 513-518. (in Chinese) |
| [23] |
王华, 康荣杰, 王兴坚. 软体弯曲驱动器设计与建模[J]. 北京航空航天大学学报, 2017, 43(5): 1053-1060. WANG H, KANG R J, WANG X J. Design and modeling of soft bending driver[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(5): 1053-1060. (in Chinese) |
| [24] |
费燕琼, 庞武, 于文博. 气压驱动软体机器人运动研究[J]. 机械工程学报, 2017, 53(13): 14-18. FEI Y Q, PANG W, YU W B. Study on motion of air-driven soft robot[J]. Journal of Mechanical Engineering, 2017, 53(13): 14-18. (in Chinese) |
| [25] |
KIM H, HAN M W, SONG S H, et al. Soft morphing hand driven by SMA tendon wire[J]. Composites Part B:Engineering, 2016, 105(16): 138-148. |
| [26] |
MATHIJSSEN G, SCHULTZ J, VANDER B, et al. A muscle-like recruitment actuator with modular redundant actuation units for soft robotics[J]. Robotics and Autonomous Systems, 2015, 74(15): 40-50. |
| [27] |
史震云, 朱前成. 基于智能驱动器的软体机器人系统[J]. 北京航空航天大学学报, 2016, 42(12): 2596-2602. SHI Z Y, ZHU Q C. Based on the intelligent driver of the softrobotsystem[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(12): 2596-2602. (in Chinese) |
| [28] |
王扬威, 兰博文, 刘凯. 形状记忆合金丝驱动的柔性机械臂建模与实验[J]. 浙江大学学报, 2018, 52(4): 628-634. WANG Y W, LAN B W, LIU K. Modeling and experiment of flexible manipulator actuated by shape memory alloy wire[J]. Journal of Zhejiang University, 2018, 52(4): 628-634. (in Chinese) |
| [29] |
FEI Y Q, XU H W. Modeling and motion control of a soft robot[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1737-1742. DOI:10.1109/TIE.2016.2572670 |
| [30] |
MUTLU R, ALICI G, LI W H. A soft mechatronic microstage mechanism based on electroactive polymer actuators[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1467-1477. DOI:10.1109/TMECH.2015.2502597 |
| [31] |
谢高鹏.食品咀嚼模拟机系统的开发与研究[D].长春: 吉林大学, 2014: 10-15. XIE G P.The research and development of food chewing simulator system[D].Changchun: Jilin University, 2014: 10-15(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10183-1014295857.htm |
| [32] |
韩敬虎.咀嚼吞咽一体化仿生机器人研究[D].无锡: 江南大学, 2016: 13-19. HAN J H.Research on integrated bionic robot for chewing and swallowing[D].Wuxi: Jiangnan University, 2016: 13-19(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10295-1016273785.htm |
| [33] |
黄建龙, 解广娟, 刘正伟. 基于Mooney-Rivlin模型和Yeoh模型的超弹性橡胶材料有限元分析[J]. 橡胶工业, 2008, 55(8): 467-471. HUANG J L, XIE G J, LIU Z W. The finite element analysis of super-elastic rubber material based on Mooney-Rivlin model and Yeoh model[J]. China Rubber Industry, 2008, 55(8): 467-471. DOI:10.3969/j.issn.1000-890X.2008.08.004 (in Chinese) |
| [34] |
KOTHERA C S, JANAID M, SIROHI J, et al. Experimental characterization and static modeling of mckibben actuators[J]. Journal of Mechanical Design, 2009, 131(9): 1010-1050. |



