DS证据理论是由Dempster[1]和Shafer[2]提出并推广,该理论能够很好地对不确定信息进行表征、融合与决策,并在信息融合、风险评估、模式识别等方面[3-6]得到广泛应用。但是,在工程应用中,由于信源的测量精度,外界环境的干扰,需要处理的信息往往是冲突的。而DS证据理论中所给出的Dempster组合规则[7-10],不能有效处理高冲突信息[11-12],比如Zadeh[13]给出经典的0信任悖论算例。为了解决这一问题,相关学者提出了大量的改进算法[9, 14-16]。针对冲突证据组合规则的研究,证据理论的改进方法主要分为两大类。
一类学者认为,Dempster组合规则之所以不能很好地处理冲突证据,是因为组合规则的建立有问题。因此,这一类学者对组合规则的公式进行大量改进,提出许多新的组合规则[15-25]。Dempster组合公式的改进主要分为3类:第1类是承认DS证据理论的乘性法则,研究如何分配冲突量k[17-23],比如Smets提出新的组合规则,将冲突量分配给了空集,避免了证据理论的归一化过程[17-18];Yager提出的新的组合规则,将冲突量全部分配给了完全不确定集[19-20];PCR1~PCR6[21-23]重点研究如何将冲突量k合理地分配到各个命题,其中PCR2和PCR5应用比较广泛。第2类是改变识别框架,拓展到广义幂集,在此基础上,给出新的组合规则,比如DSmT组合规则[23]。第3类是给出加性组合规则,比如Murphy[24]组合规则。
虽然对组合规则的改进,能够一定程度上解决冲突证据的融合问题,但是效果不是很理想。目前更多的学者认为,证据理论之所以不能很好地解决冲突证据,是因为原始数据受到传感器或者环境的噪声干扰。因此,解决冲突证据组合问题的关键在于对证据进行修正。修正证据源的研究重点在于如何获取证据的折扣权重系数[17, 25-27]。证据折扣权重系数确定方法分2种。
1) 基于信息熵,通过信息的无序性,表征证据的不确定性。Höhle[28]在似然函数基础上提出Confusion度量;Yager[29]在似真度函数基础上提出Dissonance度量;Klir等[30-31]基于命题的模,给出Discord度量和Strife度量;Harmanec和Klir[32]在概率转换的基础上,提出Aggregated不确定性度量;Jousselme等[33]基于pignistic概率转换基础上,提出Ambiguity度量;Deng[34]在Shannon熵的基础上提出Deng熵,用来衡量证据的不确定性。上述给出的多种基于信息熵的不确定性度量方法,通过算例分析,都能一定程度上表征信息的不确定性。在实际应用中,当传感器获取信源的信息时,信息在产生、传输过程中,不存在不确定性,而在信息的接收方面,随着传感器的可靠性,不同传感器获取的信源信息存在着不确定性。这时,便可以利用上述提出的多种基于证据本身的不确定性,来表征证据的可靠性,从而对证据进行修正,达到有效的组合结果。本文对这一类的冲突证据组合方法不做深入的研究,根据实际应用的需求,重点分析冲突证据不确定衡量的第2类方法,即如何衡量证据之间的冲突度或者说相似度。
2) 基于距离衡量证据的不确定性[35-37]。Jousselme等[35]提出的Jousselme距离是应用最为广泛的证据距离;Yu等[9]提出支持概率(supporting probability)距离,通过计算证据被支持程度,确定证据的折扣权重;Zhou等[38]对现有的证据距离进行运算,得到新的权重系数;Liu等[15]在概率转换DSmP的基础上,提出一种新的证据距离;Yang和Han[39]利用Tran&Duckstein区间距离衡量证据的不确定性,并得到很好的融合效果。
虽然上述文献介绍了很多基于信息熵和距离的冲突证据决策方法,但是解决冲突证据组合的流程基本相同。都是先确定一种衡量证据之间支持程度的指标,并计算两两证据之间的支持程度,得到证据;然后通过支持矩阵,计算出每一条证据的折扣系数,再对证据进行折扣;最后对折扣证据进行组合。由于要计算两两证据之间的支持程度,基于这种流程处理冲突证据组合问题,计算量比较大,且计算支持向量的归一化过程不是很合理,证据组合效果不理想。
因此,本文提出基于二次组合的冲突证据决策方法流程。首先,计算证据组的PCR6组合规则;然后,计算每条证据距离组合后证据的距离,从而确定折扣系数,并对证据组进行折扣处理;最后,再一次利用PCR6组合规则,对证据进行组合。
1 理论基础记X为识别对象,U为X可能取值的集合,并且U中的所有元素互不相容,则称U为一识别框架。
假设U为对象X的识别框架,当函数m:U→[0, 1]满足条件:
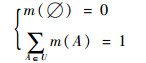
|
(1) |
则称函数m(A)为基本概率赋值(BPA),表示证据对命题A的支持程度。
假设U为一识别框架,m为BPA,定义

|
为信任函数,表示决策可能结果A所有子集信任之和,所以对于空集的信任值为Bel(∅)=0,对于全集U为Bel(U)=1。定义
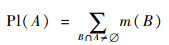
|
为似真度函数,从定义不难得到定理,Pl(A)=1-Bel(A)。信任函数与似真度函数之间满足Bel(A)≤Pl(A)。
定义区间L=[Bel(A), Pl(A)]为信任度区间,区间长度反映出命题A的不确定度。当信任度区间长度变为0时,即Bel(A)=Pl(A)时,证据理论便退化为概率论。
1) Dempster组合规则
假设m1和m2是识别框架U上的BPA,则
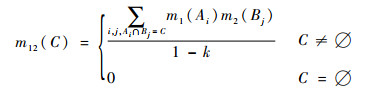
|
(2) |
式中:k为冲突系数,表达式为

|
2) PCR6组合规则
假设m1和m2是识别框架U上的BPA,则
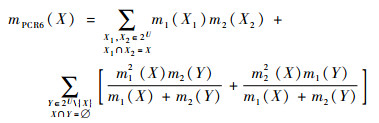
|
(3) |
Dempster组合规则在处理冲突证据时,会产生悖论现象,对于这一问题,相关学者给出多种改进方法,主要分为两类:第1类是对原有的DS证据理论的组合公式进行改进;第2类是对原始证据进行修正。目前大多数学者都接受第2类改进方式,认为证据的冲突根本上是来源于获取数据的冲突、不精确。
而对于修正证据源的冲突证据融合改进方式,已经形成一套完整的算法模型(见图 1),下面对这一模型进行构建分析。

|
| 图 1 折扣证据组合模型 Fig. 1 Discount evidence combination model |
1) 确定冲突度量函数。这是关键的一步,目前的相关修正数据源的改进算法,都是基于对不同的冲突度量函数的改进。冲突度量函数不仅需要满足物理意义,即与证据之间的距离成正相关;还需要满足数学条件,即满足范数的几条基本条件。
假设3组映射在相同命题空间U的BPA:m1(·)、m2(·)和m3(·),则存在一个映射CM(·):U×U→[0, 1]满足下列4个基本条件,被称为冲突度量函数。
① 对称性。
∀m1(·), m2(·), CM(m1, m2)=CM(m2, m1)。
② 正定性。
∀m1(·), m2(·)∈U,当m1≠m2时,CM(m1, m2)≥0;当m1=m2时,CM(m1, m2)=0。
③ 齐次性。
CM(r1m1, r2m2)=r1r2CM(m1, m2), r∈R。
④ 三角不等式。
CM(m1, m2)≤CM(m1, m3)+CM(m2, m3)。
现有的冲突度量函数大体分为两类:一类是基于信息熵的冲突度量函数,一类是基于证据之间距离的冲突度量函数。
2) 计算两两证据之间的距离,得到距离矩阵D,元素dij表示第i条矩阵与第j条证据之间的距离。距离矩阵是一个对称方阵,并且对角线的元素为0。
3) 对距离矩阵的每一列进行归一化处理,得到的矩阵第i列的一条向量,表示第i条矩阵对每一条证据的支持程度,从而便于后续的运算。
4) 将归一化后矩阵的每一行相加,得到一条向量,向量的第s个元素表示第s条证据被其他证据支持的总程度。
5) 对步骤4)得到的向量进行归一化处理,得到归一化可信度权重。
6) 利用可信度权重对证据进行折扣计算。常用的折扣公式为
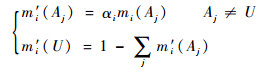
|
(4) |
式中:αi为折扣系数。
7) 对折扣后的证据进行组合,得到最后的决策证据。
2.2 基于二次组合的冲突证据决策模型通过分析折扣证据组合模型,可以发现,修正证据源的冲突证据组合方法,需要计算两两证据之间的距离,对于t证据,需要计算距离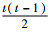

|
(5) |
式中:矩阵D中的元素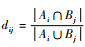
可以看出,修正证据源的冲突证据组合方法,计算量较大,不适合多条证据之间的组合(第5节将对组合规则的计算量进行定量研究),所以接下来给出一种基于二次组合的冲突证据决策模型,如图 2所示。
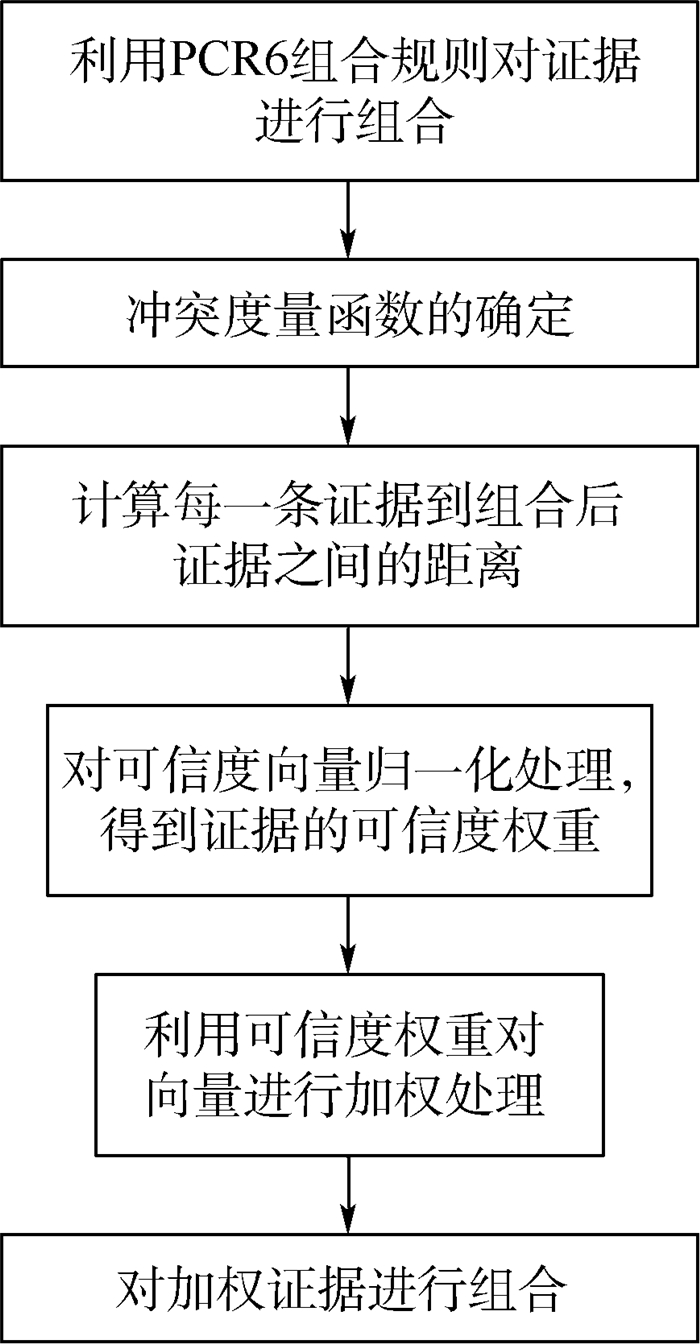
|
| 图 2 基于二次组合的冲突证据决策模型 Fig. 2 Conflict evidence decision model based on quadratic combination |
1) 利用PCR6组合规则对原有证据进行组合,得到初步的组合结果。PCR6组合被广泛地应用在冲突证据的组合规则上,并得到较好的组合效果。组合后得到的证据m′i能够一定程度上反映证据的总体水平。
2) 确定冲突度量函数,与2.1节描述的一样,度量函数需要满足范数的基本条件,这里不再赘述。
3) 计算每一条证据到组合后证据之间的距离,直接计算得到可信度向量。
4) 对证据的可信度向量进行归一化。在常规的修正证据源的冲突证据中,证据的归一化是每一项元素除以元素的和。但是从式(2)和式(3)可以看出,证据的组合规则中,证据之间的元素是进行乘法运算,即m1(Ai)m2(Aj)…mn(Ak),所以求和形式的归一化不满足计算的要求。归一化应该满足:
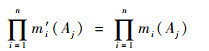
|
(6) |
为此,本文提出一种新的乘性归一化计算公式,即
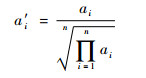
|
(7) |
归一化得到的新的权重系数,满足
5) 利用可信度对向量进行加权处理,采用折扣的方法对证据进行折扣,由于归一化公式的改变,折扣公式需要进行修正,得
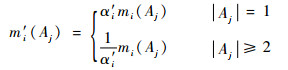
|
(8) |
式中:|Aj|表示元素的势的大小,|Aj|=1表示单元素集。
6) 利用PCR6证据组合规则对证据进行组合。
2.3 乘性组合规则的有效性分析2.2节中提出基于乘性法则的归一化公式,如式(6)和式(7)所示,下面通过算例,验证乘性归一化法则在冲突证据理论决策中的合理性。
算例1 假设4类不同传感器对目标A进行识别,识别框架为U={A, B, C},得到BPA,m1(A)=0.6, m1(B)=0.2, m1(AB)=0.1, m1(C)=0.1;m2(A)=0.6, m2(B)=0.1, m2(AB)=0.1, m2(C)=0.1, m2(BC)=0.1;m3(A)=0.5, m3(B)=0.1, m3(AB)=0.1, m3(C)=0.1, m3(AC)=0.1, m3(BC)=0.1;m4(A)=0.1, m4(B)=0.1, m4(AB)=0.1, m4(C)=0.5, m4(AC)=0.1, m4(BC)=0.1。
从BPA可以看出,前3条证据给出的A信度较高,而第4条证据出现了冲突,所以第4条证据的可信度较低,前3条证据的可信度较高,因此给出4条证据的支持度向量:
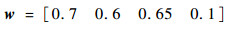
|
关于支持度向量的确定,后文第4节将根据冲突度量函数确定,这里只需论证乘性归一化法则的有效性。
然后对支持度向量分别计算加性归一化和乘性归一化之后的支持度向量,得
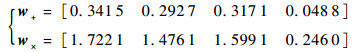
|
利用式(4)和式(8),分别计算得到折扣后的BPA,然后利用PCR6组合规则对证据进行组合,得到结果如表 1所示。表 1中:PCR6表示直接通过PCR6组合规则组合的结果;PCR6+表示通过加性归一化组合规则,再利用PCR6组合规则组合的结果;PCR6×表示通过乘性归一化组合规则,再利用PCR6组合规则组合的结果。
| 组合规则 | mi(A) | mi(B) | mi(AB) | mi(C) | mi(AC) | mi(BC) | mi(ABC) |
| PCR6 | 0.5436 | 0.0939 | 0.0403 | 0.2544 | 0.0224 | 0.0454 | 0 |
| PCR6+ | 0.5386 | 0.0938 | 0.0314 | 0.0588 | 0.0095 | 0.0205 | 0.2475 |
| PCR6× | 0.6379 | 0.0751 | 0.0622 | 0.0523 | 0.0641 | 0.1083 | 0 |
通过分析表 1中的数据可知,加性PCR6组合规则得到的不确定赋值mi(ABC)较大,因为式(4)中,加性归一化证据组合将不确定信息都赋给了命题ABC,并不利于后续的证据的决策;而本文提出的乘性归一化法则的到的组合结果显示m(ABC)=0,并且赋予命题A较大的信度,符合实际情况,得到较好的组合结果,因为乘性归一化公式与后续的PCR6组合规则中的乘法规则相呼应,这样的归一化更有意义。
2.4 预处理合理性分析2.2节中给出基于二次组合的冲突证据决策模型,首先给出PCR6组合结果为基准参考,但是后文又需要对PCR6组合规则的效果进行讨论,从逻辑上就存在了矛盾。
下面,本文将对预处理过程中,给出PCR6组合规则结果为基准证据的合理性进行证明。
算法要对多条证据进行修正,就需要考虑每条证据的冲突度程度,冲突度越大的证据,赋予它较小的权重。而冲突度的度量,已经在2.1节中介绍,要求通过求解两两证据之间的距离来衡量证据的冲突度,所以需要找出一条证据,这条证据假设为所有证据融合后的理想结果mper,然后求解所有的证据与理想证据之间的距离,从而判定每条证据的冲突度大小。
但是,理想结果mper没法求解得到,因为算法要求就是理想结果mper,这时算法便通过PCR6来近似代替理想的融合结果。
问题是,PCR6能不能代表理想结果mper作为证据的基准?本文可以通过误差分析,来判断PCR6作为基准证据的合理性。
就以表 1中的PCR6组合结果为研究对象,假设理想的证据mper与PCR6组合规则存在一定的误差,并满足以下的误差规则(可以通过这一种情况,来分析误差,判断PCR6作为基准证据的合理性):

|
通过改变α值,得到如图 3所示的误差结果。
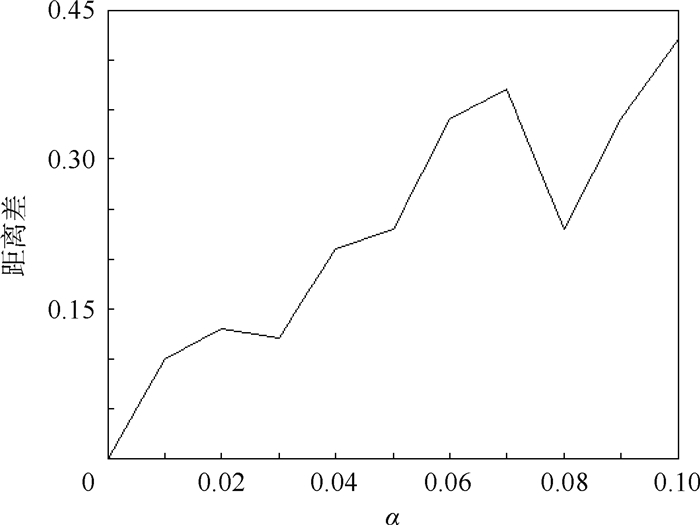
|
| 图 3 预处理误差 Fig. 3 Preprocessing error |
由图 3可以看出,当α值在0~0.1之间变化时,PCR6和证据组之间的平均距离daPCR6,与理想的证据mper和证据组之间的平均距离daper之间的差daPCR6-daper在0.05以内,误差完全可以接受。
因此,本文在预处理中给出PCR6为基准证据在一定误差范围内是合理的。
3 冲突度量函数的确定 3.1 经典的Jousselme距离冲突度量函数目前常用的冲突度量函数有两类:一类是基于信息熵的冲突度量函数;另一类是基于距离的冲突度量函数,这里的距离是一种广义的概念,包括向量距离、区间距离、角度等。信息熵是一种衡量证据离散程度的参量,一定程度上反映了证据的决策能力,根据实际应用的需求,本文不对这一类型的证据距离进行详细分析。本文将基于证据之间的距离确定冲突度量函数。
第2节已经阐明冲突度量函数需要满足的几点条件。目前最常用的冲突度量函数便是基于Jousselme距离的冲突度量函数。Jousselme距离考虑到命题的势,能够有效地衡量BPA之间的相似程度,下面给出Jousselme距离的定义。
假设m1和m2是相同识别框架下的2个BPAs,则定义m1和m2之间的Jousselme距离为

|
(9) |
式中:D为一个2|U|×2|U|的矩阵,其中的每一个元素为

|
Jousselme距离能一定程度上反映BPAs之间的距离,在数学上是严谨的,并得到广泛的应用。
Jousselme距离已经在多个领域得到了广泛的支持,但是考虑到,Jousselme距离需要求解矩阵D,运算量较大(计算量问题,本文第5节会进行进一步深入分析)。鉴于此,本文将引入向量角的概念来衡量证据之间的距离,向量之间的夹角余弦可以表示为

|
(10) |
由式(10)可以看出,证据中每一个命题的赋值满足0≤mi(Aj)≤1,所以,证据的积满足x1·x2≥0,即dθ≥0。
但是证据是基于识别框架U的2|U|维向量,单纯地将证据视为向量,求解证据之间的夹角,而丢弃证据多元素命题与单元素命题之间的差异,赋予不同命题之间相同的权重,这是不合理的,比如,对于证据组,m1(A)=0.1, m1(B)=0.5, m1(C)=0.1, m1(AC)=0.15, m1(BC)=0.15;m2(A)=0.5, m2(B)=0.1, m2(C)=0.1, m2(AC)=0.15, m2(BC)=0.15;m3(A)=0.15, m3(B)=0.15, m3(C)=0.1, m3(AC)=0.1, m3(BC)=0.5;m4(A)=0.15, m4(B)=0.15, m4(C)=0.1, m4(AC)=0.5, m4(BC)=0.1。
计算可以得到m1、m2与m3、m4之间的向量角余弦为dθ(m1, m2)=dθ(m3, m4)=0.508,即m1、m2与m3、m4之间的向量角余弦相等。但是通过分析可以发现,证据m1、m3之间,向量的大小没变,只是将命题A、B的信任度与命题AC、BC之间的信任度进行了调换,即向量m1经过旋转得到向量m3,同样m2也是经过旋转得到m4,且两者的旋转方向与角度相等,都是只改变了命题A、B与命题AC、BC之间的信任度,所以,从向量的角度分析,两者的向量角余弦相等。但因为证据的命题的势不相同,所以命题的权重应该不一样,证据m1、m2之间命题A、B冲突,其余的命题不冲突;而证据m3、m4之间命题AC、BC冲突,其余的命题不冲突,并且两对的冲突大小相同,但是由于命题A、B的可信度更高,而命题AC、BC的信度相对模糊,所以,证据m1、m2之间的距离应该大于证据m3、m4之间的距离,而单纯地通过向量的夹角并不能充分考虑到命题的势的大小,所以并不能很好地衡量证据之间的距离。因此,3.2节将考虑命题的势的大小,给出基于pignistic向量角的冲突证据度量函数。
3.2 基于pignistic向量角的冲突证据度量函数本节将结合pignistic概率转换与向量角的概念,提出基于pignistic向量角的冲突证据度量函数,即

|
(11) |
式中:BetPi为pignistic概率转换后的概率向量。向量中每一个元素为概率转换结果BetPk(Ai)为
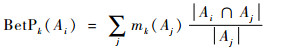
|
(12) |
下面对式(11)的对称性、正定性、齐次性和三角不等式性质进行证明。
证明 1)对称性
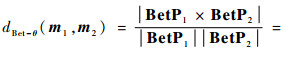
|

|
成立。
2) 正定性
因为mk(Ai)≥0, 并且BetPk(Ai)=
又因为

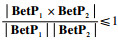
当m1=m2时,
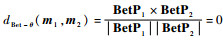
正定性成立。
3) 齐次性
在此不作证明,因为证据需要满足式(1),所以不存在比较k1m1、k2m2之间距离的情况。
4) 三角不等式
根据不等式sin θ1≤sin θ2+sin θ3,其中,θ1、θ2和θ3为空间三向量两两之间的夹角,得
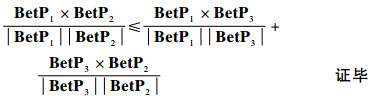
|
本节将重点分析基于二次组合的冲突证据决策的计算量。分析流程图 1和图 2,可以看出,改进后的冲突证据决策与改进前的区别在于如何获取距离矩阵,而后续对于距离矩阵的处理步骤几乎不变。所以,本文就生成距离矩阵的计算量进行分析。
首先对传统的修正数据源的冲突证据决策方法进行分析。流程图 1中的证据距离以经典的Jousselme距离为例。运算过程中的交集、并集、求势、加减乘除都记为一次运算。如式(5)所示,Jousselme距离需要求解矩阵D,运算量为

|
式中:n为识别框架U的势|U|,所以两条证据之间的Jousselme距离计算量为

|
为了得到距离矩阵,需要计算两两证据之间的距离,假设证据的数目为b,则基于Jousselme距离的冲突证据决策方法需要的计算量大小为

|
(13) |
下面对基于二次组合的冲突证据决策的计算量进行分析。分析流程图 2可知,需要对b条证据进行PCR6组合,通过分析式(3),可以得到,b条证据的PCR6组合计算量为
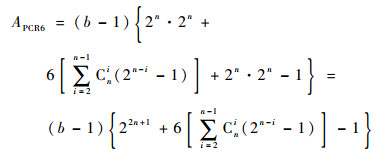
|
(14) |
式中: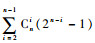

|
(15) |
式中: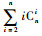

|
(16) |
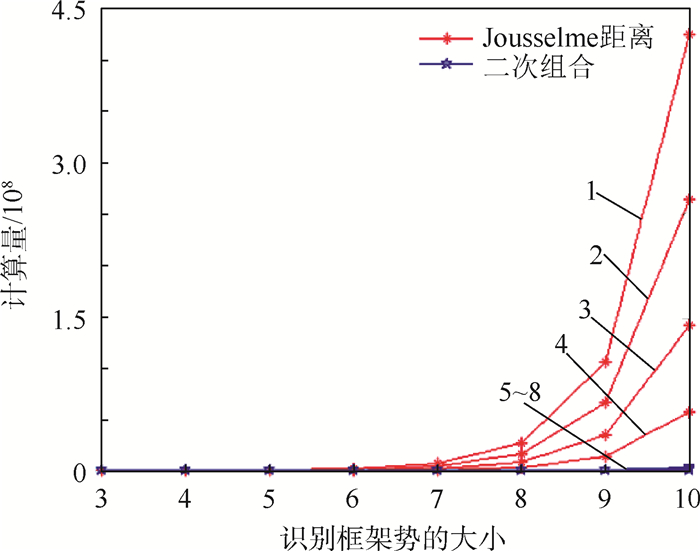
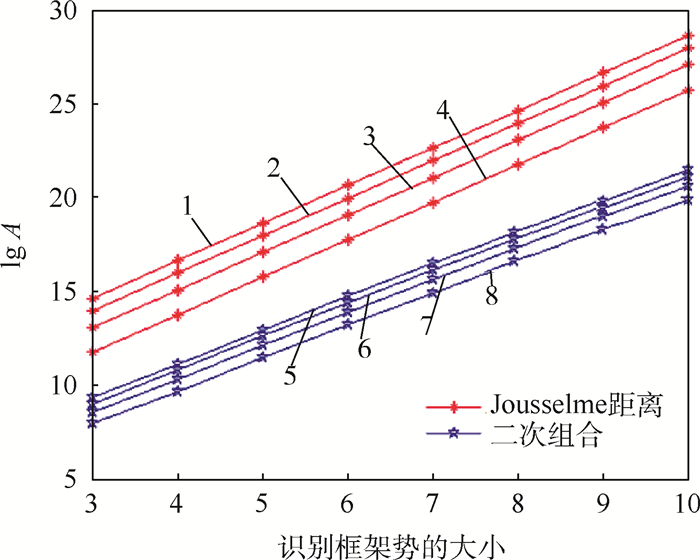
通过式(13)~式(16),对冲突证据决策方法的计算量进行分析,得到结果如图 4所示。图中,曲线1~4表示基于Jousselme距离的冲突证据决策方法的计算量,4条曲线由下至上,分别表示当证据为4~10(步长为2)时的计算量曲线,曲线5~8表示基于二次组合的冲突证据决策方法的计算量,同样4条曲线由下至上,分别表示当证据为4~10(步长为2)时的计算量曲线,横坐标表示识别框架的势的大小|U|,纵坐标表示计算量。但是,由于曲线5~8增长比较缓慢,为了便于观察分析,计算量取对数lg A,得到新的计算量增长图如图 5所示。由图 5可以看出,基于Jousselme距离和基于二次组合的冲突证据决策方法的计算量的对数,近似于线性增长,所以两者原计算量都是成指数增长。
|
| 图 4 基于Jousselme距离和二次组合的冲突证据决策计算量图 Fig. 4 Graph of calculated amount of conflict evidence decision based on Jousselme distance and quadratic combination |
|
| 图 5 基于Jousselme距离和二次组合的冲突证据决策计算量的对数图 Fig. 5 Graph of logarithm of calculated amount of conflict evidence based on Jousselme distance and quadratic combination |
结合图 4和图 5可知,当证据的个数一定时,基于Jousselme距离和基于二次组合的冲突证据决策方法的计算量的对数,呈指数增长,并且基于Jousselme距离的冲突证据决策方法的计算量增长速度比基于二次组合的快将近5~10dB;当识别框架的势一定时,计算量随着证据数的增加急剧增加。
综上分析,相比于原有的修正数据源的冲突证据决策方法,本文提出的基于二次组合的冲突证据决策方法的计算量得到了较大的改善。
5 基于二次组合的冲突证据决策算例分析算例2 考虑识别框架U={A, B, C}, 并给出6个信源的BPAs赋值,如表 2所示。
| mi(·) | BPA | ||||||
| A | B | AB | C | AC | BC | ABC | |
| m1 | 0.7 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 |
| m2 | 0.6 | 0.2 | 0 | 0.1 | 0 | 0 | 0.1 |
| m3 | 0.6 | 0.05 | 0 | 0.05 | 0 | 0 | 0.3 |
| m4 | 0.4 | 0.3 | 0 | 0.2 | 0.1 | 0 | 0 |
| m5 | 0.1 | 0.7 | 0 | 0.1 | 0 | 0 | 0.1 |
| m6 | 0.9 | 0.05 | 0 | 0.05 | 0 | 0 | 0 |
根据流程图 2,首先利用PCR6对证据组合,得到组合证据mPCR6为

|
利用式(11)和式(12),计算每一条证据与组合证据mPCR6之间的距离,得到支持向量为

|
可以看出,第5条证据m5的支持度较低,由表 3可以看出,第5条证据与其他5条证据相冲突。然后利用式(7),对权重w进行归一化,得
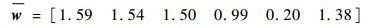
|
| mi′(·) | BPA | ||||||
| A | B | AB | C | AC | BC | ABC | |
| m′1 | 0.74 | 0.11 | 0.04 | 0.11 | 0 | 0 | 0 |
| m′2 | 0.64 | 0.21 | 0 | 0.11 | 0 | 0 | 0.05 |
| m′3 | 0.72 | 0.06 | 0 | 0.06 | 0 | 0 | 0.16 |
| m′4 | 0.40 | 0.30 | 0 | 0.20 | 0.10 | 0 | 0 |
| m′5 | 0.03 | 0.21 | 0 | 0.03 | 0 | 0 | 0.73 |
| m′6 | 0.90 | 0.05 | 0 | 0.05 | 0 | 0 | 0 |
再利用式(8),对表 2中证据组进行折扣计算,得到新的证据组,结果如表 3所示。
最后利用PCR6组合规则对折扣证据进行组合,得到结果如表 4所示。
| 组合规则 | mi(A) | mi(B) | mi(AB) | mi(C) | mi(AC) | mi(BC) | mi(ABC) |
| PCR1 | 0.57 | 0.22 | 0.02 | 0.10 | 0.02 | 0 | 0.08 |
| PCR2 | 0.57 | 0.22 | 0.02 | 0.10 | 0.02 | 0 | 0.08 |
| PCR3 | 0.67 | 0.24 | 0 | 0.06 | 0 | 0 | 0.04 |
| PCR5 | 0.46 | 0.35 | 0.01 | 0.07 | 0.01 | 0 | 0.10 |
| PCR6 | 0.72 | 0.21 | 0 | 0.03 | 0 | 0 | 0.04 |
| 本文方法 | 0.77 | 0.07 | 0 | 0.02 | 0 | 0 | 0.14 |
由表 2可以看出,第4条证据分别赋予目标A、B的BPA分别为0.4、0.3,所以第4条证据的不确定较高;而第5条证据赋予目标A、B的BPA分别为0.1、0.7,即证据5比较信任目标B,而其余的4条证据都赋予目标A较高的信度,所以证据5是一条冲突度较高的证据。通过分析可知,6条证据的组合结果应该偏向目标A。由表 4可知,相比于其他几种常见的组合方法,本文提出的基于二次组合的冲突证据决策方法得到较好的组合结果,有效地解决冲突证据组合问题。
6 结论本文针对现有冲突证据决策方法存在的一系列问题,提出新的基于二次组合的冲突证据决策方法。首先本文通过分析现有基于修正数据源的冲突证据决策方法的一般流程,给出新的基于二次组合的冲突证据决策方法流程图,并给出乘性归一化规则。算例研究表明,由于乘性归一化规则与证据理论组合规则的乘性法则相呼应,能得到更好的组合效果。其次,通过分析现有冲突度量函数的不足,提出基于pignistic向量角的冲突证据度量函数,并通过分析得到新的证据度量函数,满足范数理论的对称性、正定性、齐次性和三角不等式性质。然后,对基于二次组合的冲突证据决策的计算量进行分析,通过与原有证据理论方法的比较发现,新方法相比于现有方法,计算量减少将近5~10 dB,计算量得到较大的改进。最后,通过与不同组合规则的比较发现,所提新方法在处理冲突证据组合时,能得到更好的组合效果。
| [1] |
DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. Annals of Mathematical Statistics, 1967, 38(2): 325-339. DOI:10.1214/aoms/1177698950 |
| [2] |
SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976: 85-150.
|
| [3] |
XU Z, HU C, YANG F, et al. Data-driven inter-turn short circuit fault detection in induction machines[J]. IEEE Access, 2017, 5: 25055-25068. DOI:10.1109/ACCESS.2017.2764474 |
| [4] |
WANG X, YANG F, WEI H, et al. A risk assessment model of uncertainty system based on set-valued mapping[J]. Journal of Intelligent and Fuzzy Systems, 2016, 31(6): 3155-3162. DOI:10.3233/JIFS-169201 |
| [5] |
ZHANG X, MAHADEVAN S, DENG X. Reliability analysis with linguistic data:An evidential network approach[J]. Reliability Engineering and System Safety, 2017, 162: 111-121. DOI:10.1016/j.ress.2017.01.009 |
| [6] |
JIANG W, XIE C, ZHUANG M, et al. Failure mode and effects analysis based on a novel fuzzy evidential method[J]. Applied Soft Computing, 2017, 57: 672-683. DOI:10.1016/j.asoc.2017.04.008 |
| [7] |
HAN D, DEZERT J, YANG Y. Belief interval-based distance measures in the theory of belief functions[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2016, 99: 1-18. |
| [8] |
QIAN J, GUO X F, DENG Y. A novel method for combining conflicting evidences based on information entropy[J]. Applied Intelligence, 2017, 46(4): 876-888. DOI:10.1007/s10489-016-0875-y |
| [9] |
YU C, YANG J, YANG D, et al. An improved conflicting evidence combination approach based on a new supporting probability distance[J]. Expert Systems with Applications, 2015, 42(12): 5139-5149. DOI:10.1016/j.eswa.2015.02.038 |
| [10] |
SMARANDACHE F, DEZERT J.Modified PCR rules of combination with degrees of intersections[C]//International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2015: 2100-2107.
|
| [11] |
JIANG W, LUO Y, QIN X, et al. An improved method to rank generalized fuzzy numbers with different left heights and right heights[J]. Journal of Intelligent and Fuzzy Systems, 2015, 28(5): 2343-2355. DOI:10.3233/IFS-151639 |
| [12] |
JIANG W, WEI B, QIN X, et al. Sensor data fusion based on a new conflict measure[J]. Mathematical Problems in Engineering, 2016, 2016: 5769061. |
| [13] |
ZADEH L A. A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination[J]. AI Magazine, 1986, 7(2): 85-90. |
| [14] |
LIU Z G, DEZERT J, PAN Q, et al. Combination of sources of evidence with different discounting factors based on a new dissimilarity measure[J]. Decision Support Systems, 2011, 52(1): 133-141. DOI:10.1016/j.dss.2011.06.002 |
| [15] |
MARTIN A, JOUSSELME A L, OSSWALD C.Conflict measure for the discounting operation on belief functions[C]//International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2008: 1-8.
|
| [16] |
YANG Y, HAN D, HAN C. Discounted combination of unreliable evidence using degree of disagreement[J]. International Journal of Approximate Reasoning, 2013, 54(8): 1197-1216. DOI:10.1016/j.ijar.2013.04.002 |
| [17] |
DENG X Y, HU Y, DENG Y, et al. Environmental impact assessment based on D numbers[J]. Expert Systems with Applications, 2014, 41(2): 635-643. DOI:10.1016/j.eswa.2013.07.088 |
| [18] |
FEI L G, HU Y, XIAO F Y, et al. A modified TOPSIS method based on D numbers and its applications in human resources selection[J]. Mathematical Problems in Engineering, 2016, 2016: 6145196. |
| [19] |
BIAN T, ZHENG H Y, YIN L K, et al. Failure mode and effects analysis based on D numbers and TOPSIS[J]. Knowledge-based Systems, 2016, 2016: 1-39. |
| [20] |
SU X Y, MAHADEVAN S, XU P D, et al. Dependence assessment in human reliability analysis based on D numbers and AHP[J]. Risk Analysis, 2015, 35(7): 1296-1316. DOI:10.1111/risa.2015.35.issue-7 |
| [21] |
DENG X Y, HU Y, DENG Y. Supplier selection using AHP methodology extended by D numbers[J]. Expert Systems with Applications, 2014, 41(1): 156-167. DOI:10.1016/j.eswa.2013.07.018 |
| [22] |
FANG C, ZHONG D H, YAN F G, et al. A hybrid fuzzy evaluation method for curtain grouting efficiency assessment based on an AHP method extended by D numbers[J]. Expert Systems with Applications, 2016, 44(1): 289-303. |
| [23] |
DENG X Y, LU X, CHAN F T, et al. D-CFPR:D numbers extended consistent fuzzy preference relations[J]. Knowledge-based Systems, 2015, 73: 61-68. DOI:10.1016/j.knosys.2014.09.007 |
| [24] |
ZHOU X Y, SHI Y Q Y, DENG Y, et al. D-DEMATEL:A new method to identify critical success factors in emergency management[J]. Safety Science, 2017, 91: 93-104. DOI:10.1016/j.ssci.2016.06.014 |
| [25] |
LIU W. Analyzing the degree of conflict among belief functions[J]. Artificial Intelligence, 2006, 170(11): 909-924. DOI:10.1016/j.artint.2006.05.002 |
| [26] |
KHATIBI V, MONTAZER G A. A new evidential distance measure based on belief intervals[J]. Scientia Iranica, 2010, 17(2): 119-132. |
| [27] |
CHEN J, YE F, JIANG T, et al. Conflicting information fusion based on an improved DS combination method[J]. Symmetry, 2017, 9(11): 278. DOI:10.3390/sym9110278 |
| [28] |
HÖHLE U.Entropy with respect to plausibility measures[C]//Proceedings of the 12th IEEE International Symposium on Multiple-Valued Logic.Piscataway, NJ: IEEE Press, 1982: 167-169.
|
| [29] |
YAGER R R. Entropy and specificity in a mathematical theory of evidence[J]. International Journal of General Systems, 2008, 219(4): 291-310. |
| [30] |
KLIR G J, RAMER A. Uncertainty in the Dempster-Shafer theory:A critical re-examination[J]. International Journal of General Systems, 1990, 18(2): 155-166. DOI:10.1080/03081079008935135 |
| [31] |
KLIR G J, PARYIZ B.A note on the measure of discord[C]//8th International Conference on Uncertainty in Artificial Intelligence.San Francisco: Morgan Kaufmann Publishers Inc., 1992: 138-141.
|
| [32] |
HARMANEC D, KLIR G J. Measuring total uncertainty in Dempster-Shafer theory:A novel approach[J]. International Journal of General Systems, 1994, 22(4): 405-419. DOI:10.1080/03081079408935225 |
| [33] |
JOUSSELME A L, LIU C, GRENIER D, et al. Measuring ambiguity in the evidence theory[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2006, 36(5): 890-903. DOI:10.1109/TSMCA.2005.853483 |
| [34] |
DENG Y. Deng entropy:A generalized Shannon entropy to measure uncertainty[J]. Chaos, Solitons & Fractals, 2016, 91: 549-553. |
| [35] |
JOUSSELME A L, GRENIER D, BOSSÉ É. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(2): 91-101. DOI:10.1016/S1566-2535(01)00026-4 |
| [36] |
DING J, HAN D, DEZERT J, et al.Comparative study on BBA determination using different distances of interval numbers[C]//International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2017: 1-6.
|
| [37] |
YANG Y, HAN D, DEZERT J, et al.Comparative study of focal distance measures in theory of belief functions[C]//International Conference on Information Fusion.Piscataway, NJ: IEEE Press, 2017: 979-984.
|
| [38] |
ZHOU D, PAN Q, CHHIPI-SHRESTHA G, et al. A new weighting factor in combining belief function[J]. PLOS ONE, 2017, 12(5): e0177695. DOI:10.1371/journal.pone.0177695 |
| [39] |
YANG Y, HAN D. A new distance-based total uncertainty measure in the theory of belief functions[J]. Knowledge-Based Systems, 2016, 94: 114-123. DOI:10.1016/j.knosys.2015.11.014 |



