2. 奥尔良大学 MAPMO研究所, 奥尔良 45000;
3. 北京航空航天大学 经济管理学院, 北京 100083
2. MAPMO, University of Orleans, Orleans 45000, France;
3. School of Economics and Management, Beihang University, Beijing 100083, China
在概率统计中,Dirichlet分布是一类包含正参数向量的连续多元概率分布。现实生活中很多常见的数据都满足Dirichlet分布,例如三次产业比例结构数据,如果各个产业比例之和为1,那么就服从一个Dirichlet分布。该分布被广泛应用在比例结构数据问题当中。
对Dirichlet混合分布进行估计,并且对Dirichlet混合样本进行精确类别划分具有十分重要的意义。Fraley和Raftery[1]对一些经典的混合分布数据,例如高斯混合分布,总结了其混合模型的参数估计方法。在一系列的研究中,主要有2种不同的方法被用于解决混合模型的分解问题。
最广泛运用的一种方法是把混合分布的分解问题转化为一个估计问题,目标是估计出混合分布模型的参数,通常利用极大似然估计方法。1977年,Dempster[2]提出的最大期望(Expectation Maximization, EM)算法便是解决此类问题的基础优化算法。在此基础上,多种针对不同情形的EM算法的更新版本或适应版本被陆续提出,包括Celeux和Govaert[3-4]提出的随机EM(Stochastic EM, SEM)算法、分类EM(Classification EM,CEM)算法、Tanner和Wong[5]提出的蒙特卡罗EM(Monte Carlo EM, MCEM)算法,以及Render[6]提出的一些其他版本,更多具体内容介绍可以参考Peel和McLachlan[7]的研究。
另一种方法则是基于聚类算法的思想。这些方法考虑将包含n个观测的混合样本划分为K个类别,其中每个类别的观测都服从于一个共同的概率密度分布。这一类方法中最基础的为动态聚类算法[8-10]。Celeux和Govaert[4]正是将这类方法和EM算法的理念相融合才提出了CEM算法。
其他较为经典的方法还有迭代重定位算法[8, 11]、层次分类算法[12]、神经网络算法[13-14]、重叠分类算法(例如可加聚类算法[15]、金字塔算法[16]和函数聚类模型[17-18])。诸多近期研究还将Copula函数应用于混合模型之中[19-21]。
根据对文献的整体梳理,EM算法和动态聚类算法是2种处理混合分布问题的核心方法。然而,已有研究大多针对的是高斯分布等经典分布类型,其分布形式较为简单。而对于Dirichlet混合分布的研究少有提及,然而这类分布在处理比例结构数据时具有重大价值。因此,本文提出Dirichlet混合样本的EM算法和动态聚类算法,并通过数字仿真实验对2种算法的效果进行了比较,从而总结出2种算法各自的优势及其适用的情形。
1 两种机器学习聚类算法令随机向量p=[p1, p2, …, pK]的各个元素值都大于0且总和为1,这样pk(k=1, 2,…, K)就代表第k项的比例。在具有参数向量α的Dirichlet分布中,p的概率密度为
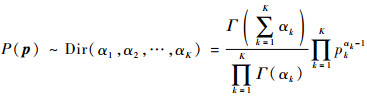
|
(1) |
式中:pk>0,且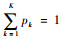
在统计领域中,EM算法通常被用来寻找依赖于不可观察的隐性变量的概率模型中参数的最大似然估计,是一种迭代算法。其在高斯混合模型中已经得到了广泛的应用。由于Dirichlet分布较为复杂,EM算法在Dirichlet混合分布中的应用较少。接下来,将介绍Dirichlet混合样本的EM算法推导过程。
设x=[x1, x2, …, xn]为一个Dirichlet混合样本,该样本数据由m个Dirichlet分布产生,每个Dirichlet分布包含k个参数。令z=[z1, z2, …, zn]为隐藏的类别标签变量,该标签决定了观测与Dirichlet分布的对应关系。因此,有
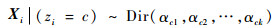
|
(2) |
式中:类别参数c=1, 2, …, m,P(zi=c)=τc且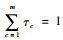
本文目标是估计出Dirichlet混合分布的未知参数θ=(τc, αcj), c=1, 2, …, m; j=1, 2, …, k。
对于该Dirichlet混合样本,其完整数据的似然函数为
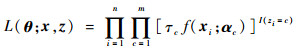
|
(3) |
式中:αc=[αc1, αc2, …, αck]为第c类样本的Dirichlet参数向量; I为指示性函数。
结合Dirichlet分布的概率密度函数:

|
(4) |
可以得到全数据对数似然函数,即
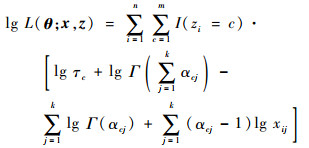
|
(5) |
在E步中,已知第t次迭代得到的参数估计值θ(t),zj的条件分布可以按照贝叶斯定理得到,其计算公式为

|
(6) |
此外,计算完整数据对数似然函数的期望Q为
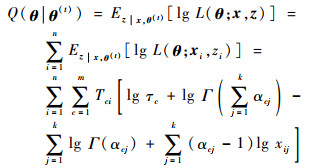
|
(7) |
可以看出,τc和αcj出现在Q的不同线性项中,因此可以分别通过极大化求导,得出迭代估计值,这也是M步的主要内容。
在M步中,与其他混合分布模型相同,权重参数τc的计算公式为
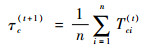
|
(8) |
而对于参数(αc1, αc2, …, αck),其估计值的更新公式为
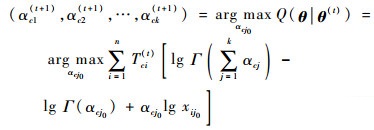
|
(9) |
对于混合模型中的每一个Dirichlet分布,可以得到k个包含k个参数的方程,通过求解联立方程组,就可以得到每个Dirichlet分布参数(αc1, αc2, …, αck), c=1, 2, …, m的估计值。
设ε为精度参数,当Ez|x, θ(t)[lg L(θ(t); x, z)]-Ez|x, θ(t-1)[lg L(θ(t-1); x, z)]≤ε时,迭代过程终止。
Dirichlet样本的EM算法的计算过程可以归纳为如下4个步骤:
步骤1 随机初始化Dirichlet分布参数α(0)和权重参数τ(0)。同时,设置精度参数ε。
步骤2 根据式(6)和式(8),计算出τ(1)。
步骤3 计算函数Q。通过式(7)和式(9),可得到Dirichlet分布参数下一步估计α(1)。计算Ez|x, θ(t)[lg L(θ(t); x, z)]-Ez|x, θ(t-1)[lg L(θ(t-1); x, z)],与ε进行比较。
步骤4 重复进行步骤2和步骤3,直到迭代到第t次时,2次期望对数似然函数值之差小于精度参数值,即Ez|x, θ(t)[lg L(θ(t); x, z)]-Ez|x, θ(t-1)[lg L(θ(t-1); x, z)] < ε,此时迭代达到了终止条件,计算过程结束。
1.2 Dirichlet混合样本的动态聚类算法动态聚类是一种快速估计出样本观测所属类别的常用方法。它的核心思想是在初始化观测所属类别后,通过计算似然值进行逐步迭代,不断更新观测类别和类分布参数,直到迭代收敛。接下来,本文将给出Dirichlet样本的动态聚类算法。
给定一个Dirichlet混合样本,样本包含n个独立观测x=[x1, x2, …, xn],这些观测来自m个Dirichlet分布。每一步迭代过程的目的是估计出每个Dirichlet概率密度函数的参数,使得按照该类别划分计算得到的聚类准则参数例如似然值达到最优。
对于每个类别,需要估计其分布参数(αc1, αc2, …, αck)。得到m个Dirichlet概率密度函数后,可以计算出每个观测的m个概率密度值。通过极大化联合概率密度,每个观测被归为不同的类别。这个过程得到了一个新的类别划分。动态聚类则是重复该过程直至对数似然函数达到收敛临界值。对数似然函数方程为
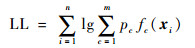
|
(10) |
式中:pc为每个类别的权重;fc(·)为每个类别的Dirichlet密度函数。
Dirichlet样本的动态聚类算法的计算过程可以归纳为如下4个步骤:
步骤1 随机初始化原始观测的类别划分。将x=[x1, x2, …, xn]划分为m个类别,得到类别划分C(0)=[C1(0), C2(0), …, Cm(0)]。
步骤2 根据m个类别中每一类别的观测,分别估计出m个Dirichlet密度函数f1(0)(·), f2(0)(·), …, fm(0)(·)的参数值。然后计算这一步的对数似然函数值。
步骤3 对于每一个观测xi,代入到m个Dirichlet密度函数中,得到f1(0)(xi), f2(0)(xi), …, fm(0)(xi)。然后将观测划分到Dirichlet密度值最大的类别。遍历n个观测后,得到新的类别划分C(1)=[C1(1), C2(1), …, Cm(1)]。
步骤4 重复步骤2和步骤3,当2次迭代过程的对数似然函数值之差的绝对值|LL(s)-LL(s-1)| < ε时,动态聚类算法终止。其中,ε为预设的精度参数。
2 数字仿真实验本节将生成Dirichlet混合样本,并运用提出的Dirichlet EM算法和动态聚类算法分别对混合样本进行聚类,然后比较2种算法聚类效果。仿真实验过程的实现全部基于R统计分析软件。
2.1 仿真数据的生成为了便于计算,生成样本量为1 000的Dirichlet样本,样本中的每个观测为一个二维向量,向量元素值介于0到1之间,且各元素之和为1。并且1 000个观测分别源自2个不同的类别C1和C2。C1包含300个观测,而C2包含700个观测。此外,C1和C2分别满足不同的Dirichlet分布,其中xi∈C1~Dir(2, 3),xj∈C2~Dir(7, 4)。精度参数ε=0.001,即当2次迭代的对数似然函数值之差小于0.001时,算法终止。
2.2 评价指标共提出6个评价指标用于2种算法的比较。第1个指标为对数似然函数值,该指标衡量不同迭代次数间对原始样本拟合水平的差异。第2个指标为程序运行时间,第3个指标为收敛迭代次数,这2个指标共同衡量算法的运行效率。运行时间越短,迭代次数越少,则算法的运行效率越高。第4个指标为聚类正确率,用于衡量2种算法得到的类别划分结果与真实类别划分结果的一致程度,正确率越高,则与真实类别的一致程度越高。这里需要指出的是EM算法实质上是一种模糊聚类算法,它给出的是每一个观测属于各个类别的概率值,概率值大小反映观测属于该类别的倾向大小。因此,用EM算法进行类别划分,默认的前提假设是将每个观测归到概率值最大的类别。最后2个指标为真正率(True Positive Rate, TPR)和假正率(False Positive Rate, FPR),用以检测非平衡二分类样本中正负样本的识别效率。TPR为正确预测的正样本占所有正样本的比例,该指标值越大越优。FPR为被错分为正样本的负样本占所有负样本的比例,该指标值越小越优。
2.3 仿真实验过程一共设计2个数字仿真实验,第1个仿真实验比较2种机器学习算法在单个Dirichlet混合样本中的聚类效果,第2个仿真实验则通过多次重复实验,削弱偶然因素影响,进而比较2种算法的聚类效果。具体操作如下:
1) 仿真实验一
按照2.1节的描述生成一个样本量为1 000的Dirichlet混合样本,其中300个观测满足Dirichlet分布Dir(2, 3),剩余700个观测满足Dirichlet分布Dir(7, 4),然后比较EM算法和动态聚类算法在6个评价指标上的效果。
2) 仿真实验二
按照仿真实验一,生成100个Dirichlet混合样本,并重复仿真实验一100次,然后计算100次实验得到的6个评价指标的平均值。对于每次仿真实验,2种算法都应用于同一个Dirichlet混合样本。
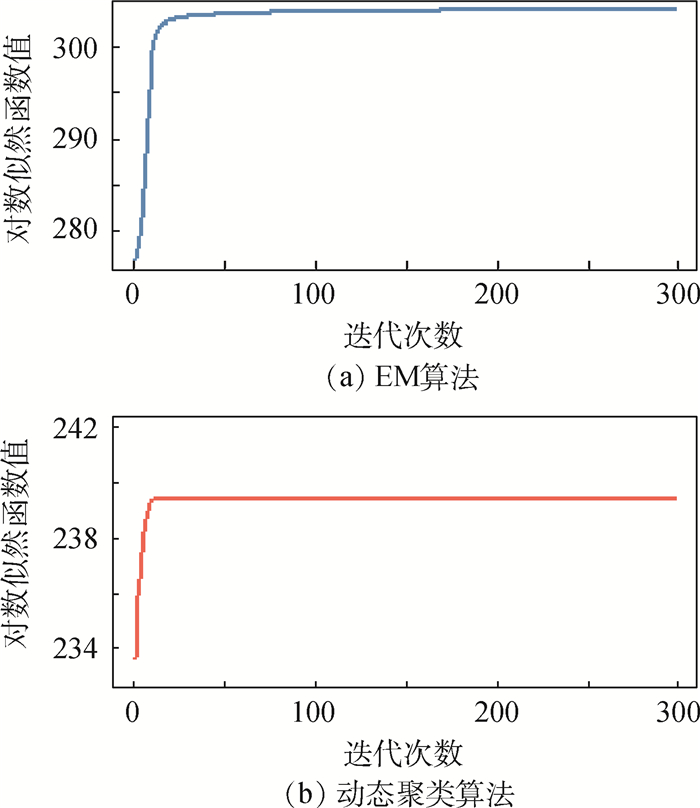
3 结果与讨论首先,比较仿真实验一各评价指标的结果。图 1分别展示了EM算法和动态聚类算法的对数似然函数曲线随迭代次数的变化情况。
|
| 图 1 EM算法与动态聚类算法在300次迭代过程中的对数似然函数曲线 Fig. 1 Log-likelihood function curves of EM algorithm and dynamical clustering algorithm during 300 times of iteration |
EM算法与动态聚类2种算法的对数似然函数曲线都呈现单调递增趋势。300次迭代终止时,动态聚类算法对数似然函数值为239.36,EM算法的对数似然函数值为304.15。此外,二者的迭代次数也不同,EM算法运行了190次后达到收敛精度,而动态聚类算法只经过13次迭代后就达到所需要的收敛精度。
在程序运行时间上,EM算法一次迭代平均耗时为0.022 s,而动态聚类一次迭代平均耗时为0.068 s。但是,由于达到预设精度所需要的迭代次数不同,当达到迭代终止条件时,EM算法需要3.61 s的运行时间,而动态聚类算法具有更优的效果,只需要1.19 s运行时间。
对于类别划分结果,表 1展示了2种算法的聚类结果。根据表中结果,计算出EM算法的正确率为79.9%,而动态聚类算法的正确率为69.4%。这表明EM算法的整体预测准确性要优于动态聚类算法。
| 算法 | 真实类别 | 仿真类别 | |
| 1 | 2 | ||
| EM算法 | 1 | 172 | 128 |
| 2 | 73 | 627 | |
| 动态聚类算法 | 1 | 235 | 65 |
| 2 | 241 | 459 | |
以C1为正样本,计算出EM算法的TPR和FPR分别为57.3%和10.4%,而动态聚类算法的TPR和FPR分别为78.3%和34.4%。这表明2种算法呈现出不同的聚类特征。EM算法的FPR更小,对C2具有相对更佳的识别效率,而动态聚类的TPR更大,对类别1具有相对更佳的识别效率。
接下来,生成100个Dirichlet混合样本,对于每个样本分别进行第1个仿真实验,得到100组仿真实验结果。为了比较2种算法,分别计算各评价指标的100次仿真平均值,结果见表 2。
| 评价指标 | EM算法 | 动态聚类算法 |
| 程序运行时间/s | 2.106 | 1.390 |
| 收敛迭代次数 | 121.51 | 20.25 |
| 聚类正确率/% | 80.5 | 71.3 |
| TPR/% | 59.9 | 77.3 |
| FPR/% | 8.6 | 31.1 |
从表 2可以看出,在程序运行时间、收敛迭代次数和TPR 3个指标上,动态聚类算法的表现要优于EM算法,而对于聚类正确率和FPR 2个评价指标,EM算法表现更优。这一结论表明,针对Dirichlet混合样本,动态聚类算法能够快速给出样本类别划分结果,但是聚类正确率稍有牺牲,而在时间要求较为宽松的情况下EM算法则能够给出更加精确的类别划分结果。此外,EM算法的平均对数似然函数值为289.22,而动态聚类算法的平均对数似然函数值为214.83。
进一步比较2种算法的TPR与FPR指标,基本与仿真实验一的结果保持一致。EM算法的FPR较小,表明第2类样本被错误预测为第1类的情况越少,即对类别2的识别效率更优。而动态聚类算法的TPR较大,表明被正确预测的第1类样本更多,即对类别1的识别效率更优。
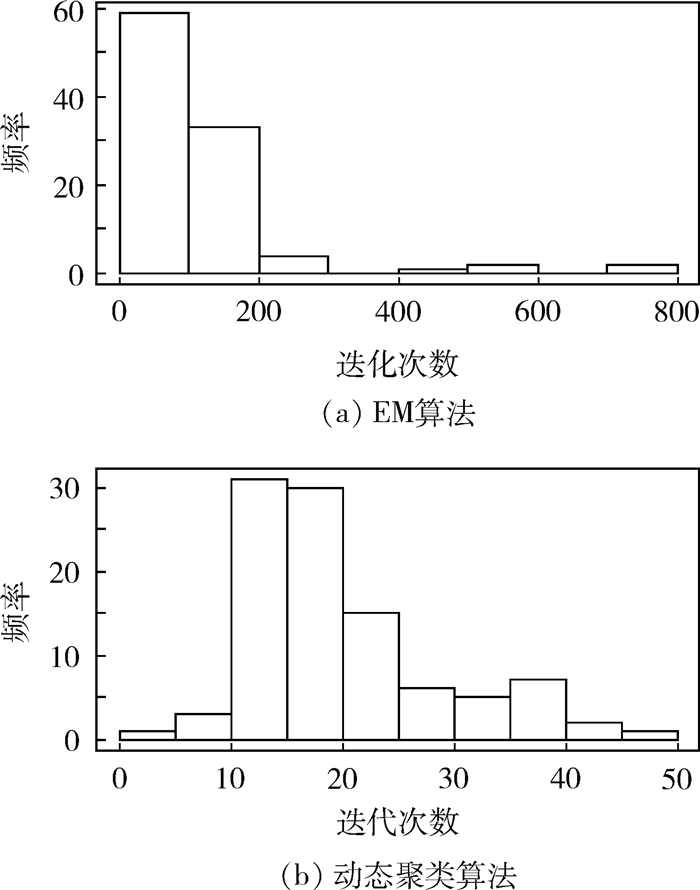
在达到收敛所需的迭代次数分布上,EM算法与动态聚类算法二者都呈现出正偏态特征,如图 2所示。这表明在多次重复实验中,少数实验的随机参数初始值与最优值偏离较大,从而降低了算法优化效率,使得迭代次数增加,程序运行时间变长。根据仿真实验结果,以随机初始值与真实值的绝对距离为评价指标,比较迭代次数处于前25%与后25%的仿真实验在该指标上的差异。计算结果表明,在EM算法中前者的该项指标比后者要高出29.2%,在动态聚类算法中要高出10.9%。即迭代随机初始值离真实值偏差较大时,算法需要更多的迭代次数才能达到收敛状态。
|
| 图 2 EM算法与动态聚类算法的迭代次数直方图 Fig. 2 Histogram of iteration times for EM algorithm and dynamical clustering algorithm |
但是,整体上EM算法的迭代次数集中在0~200,而动态聚类算法的迭代次数集中在10~20,后者的计算效率明显高于前者。需要说明的是,EM算法和动态聚类算法都是局部优化算法,最终聚类结果对各观测初始类别设定有较强的依赖,并且2种算法对各个参数的随机初始值也较为敏感。因此,在使用过程中,建议多次实验,每次进行不同的参数初始化设置,再根据轮廓系数等评价指标选取理想的聚类结果。
4 结论本文针对分布形式较为复杂的Dirichlet混合样本,提出了2种聚类算法的应用,分别为EM算法和动态聚类算法,并给出EM算法的数学推导过程以及2种算法的迭代流程。
1) 仿真实验结果表明,EM算法聚类正确率更高但是运算效率相对较低,而动态聚类算法运算效率较高但是损失了部分正确率。因此在实际运用过程中,需要根据运算环境以及精度等客观需求,选取合适的算法对样本进行聚类。如果对结果的准确度要求较高,则使用EM算法;如果对运算速度要求较高,则使用动态聚类算法。
2) 需要指出的是, EM算法和动态聚类算法作为局部优化算法,对迭代初始值具有较强的敏感性,因此在算法运行过程中,建议多次运行选取效果较好的一次作为最终结果,聚类效果评价可参考轮廓系数、组间离差平方和、组内离差平方和等指标。
另外,现实情况下,不同观测之间往往具有一定的相关性,未来研究考虑将2种算法拓展到非独立Dirichlet分布情形之中。
| [1] |
FRALEY C, RAFTERY A E. Model-based clustering, discriminant analysis, and density estimation[J]. Publications of the American Statistical Association, 2002, 97(458): 611-631. DOI:10.1198/016214502760047131 |
| [2] |
DEMPSTER A P. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of Royal Statistical Society B, 1977, 39(1): 1-38. |
| [3] |
CELEUX G, GOVAERT G. Stochastic algorithms for clustering[M]. Heidelberg: Physica-Verlag, 1990.
|
| [4] |
CELEUX G, GOVAERT G. A classification EM algorithm for clustering and two stochastic versions[J]. Computational Statistics & Data Analysis, 1992, 14(3): 315-332. |
| [5] |
TANNER M A, WONG W H. The calculation of posterior distributions by data augmentation[J]. Publications of the American Statistical Association, 1987, 82(398): 528-540. DOI:10.1080/01621459.1987.10478458 |
| [6] |
RENDER E. Mixture densities, maximum likelihood and the EM algorithm[J]. SIAM Review, 1984, 26(2): 195-239. DOI:10.1137/1026034 |
| [7] |
PEEL D, MCLACHLAN G J. Robust mixture modelling using the t distribution[J]. Statistics and Computing, 2000, 10(4): 339-348. DOI:10.1023/A:1008981510081 |
| [8] |
DIDAY E, SCHROEDER A, OK Y.The dynamic clusters method in pattern recognition[C]//Proceedings of International Federation for Information Processing Congress, 1974: 691-697.
|
| [9] |
SCOTT A J, SYMONS M J. Clustering methods based on likelihood ratio criteria[J]. Biometrics, 1971, 27(1): 387-397. |
| [10] |
SYMONS M J. Clustering criteria and multivariate normal mixtures[J]. Biometrics, 1981, 37(1): 35-43. DOI:10.2307/2530520 |
| [11] |
WONG M A, LANE T. A kTH nearest neighbour clustering procedure[J]. Journal of the Royal Statistical Society, 1981, 45(3): 362-368. |
| [12] |
BROSSIER G. Piecewise hierarchical clustering[J]. Journal of Classification, 1990, 7(2): 197-216. DOI:10.1007/BF01908716 |
| [13] |
BISHOP C M. Neural networks for pattern recognition[M]. Oxford: Oxford University Press, 1995.
|
| [14] |
BOCK H H.Clustering and neural networks[M]//RIZZI A, VICHI M, BOCK H H.Advances in data science and classification.Berlin: Springer, 1998: 265-277.
|
| [15] |
ARABIE P, CARROLL J D. Mapclus:A mathematical programming approach to fitting the adclus model[J]. Psychometrika, 1980, 45(2): 211-235. DOI:10.1007/BF02294077 |
| [16] |
DIDAY E.An intuitive form of expression: Pyramids[D].Paris: INRIA, 1984.
|
| [17] |
JAMES G M, SUGAR C A. Clustering for sparsely sampled functional data[J]. Publications of the American Statistical Association, 2003, 98(462): 397-408. DOI:10.1198/016214503000189 |
| [18] |
WINSBERG S, SOETE G D. Latent class models for time series analysis[J]. Applied Stochastic Models in Business & Industry, 1999, 15(15): 183-194. |
| [19] |
VRAC M, BILLARD L, DIDAY E. Copula analysis of mixture models[J]. Computational Statistics, 2012, 27(3): 427-457. DOI:10.1007/s00180-011-0266-0 |
| [20] |
KOSMIDIS I, KARLIS D. Model-based clustering using copulas with applications[J]. Statistics and Computing, 2016, 26(5): 1079-1099. DOI:10.1007/s11222-015-9590-5 |
| [21] |
MARBAC M, BIERNACKI C, VANDEWALLE V. Model-based clustering of Gaussian copulas for mixed data[J]. Communications in Statistics-Theory and Methods, 2017, 46(23): 11635-11656. DOI:10.1080/03610926.2016.1277753 |



