2. 北京航天长征飞行器研究所, 北京 100076
2. Beijing Institute of Space Long March Vehicle, Beijing 100076, China
近年来,一种被称为“三体(triplet)协同追逃”的制导问题在制导领域形成了一个关注的热点[1-3]。这里所谓的“三体”是指由一个目标(target)和一个可保护目标免受攻击的防御武器(defender),以及一个对目标进行拦截的攻击武器(attacker)所组成的攻-防-守三方[4-6]。由于微分对策理论的主要研究对象是一类具有对抗和竞争关系的群体,所以攻-防-守三方之间的博弈关系就很自然地适合用微分对策理论加以分析和研究。
上述形式制导问题的研究首见于文献[7],文中假设目标静止或低速移动,根据初始弹目距离为目标和防御弹提出了一种闭环最优制导律。文献[8]基于微分对策和线性二次型理论,为飞行器-防御弹-攻击弹提出了一种最优制导策略,使得飞行器可以引诱攻击弹,从而使攻击弹更易被防御弹拦截,但从其仿真结果来看,当飞行器速度小于攻击弹速度时,飞行器总是会被攻击弹命中,它必须严格依靠防御弹提前将攻击弹拦截下来才可存活。文献[9-12]将基于微分对策的“三体”协同制导问题称为主动目标防御微分对策(ATDDG),并提出了一类基于最优航向的制导策略,采用这种制导律时目标和防御弹的弹道十分平直且侧向加速度的需求为零。文献[13-14]基于微分对策理论,将攻-防-守三方的角色进行了通俗化描述并对三方追逃问题进行分析。文献[15]对具有高阶自动驾驶仪动态的三方追逃问题进行了研究,并得到了对策三方的最优制导策略。文献[16-17]考虑对策各方最大可用控制受约束的情况,给攻击弹提出了一种先逃逸后追踪的制导策略。文献[18-19]也对控制有界条件下攻击弹的制导策略进行了分析,并提出了2种改进型的攻击弹制导律。
本文针对飞行器-防御弹-攻击弹的三方追逃问题进行了研究,但考虑到:①文献[9-12]提出的制导律仅给目标和防御弹提供了最优航向,不需采取侧向机动,因而弹道十分平直,但是这种方法忽略了实战当中无论飞行器、防御弹还是攻击弹都需要进行一定的机动[17];②文献[8, 13-15]提出的均是基于线性二次型形式的制导策略,这类制导策略没有考虑对策参与者的控制往往都是有界的这一实际问题,在应用中容易出现加速度饱和现象而使制导律失去最优性,产生较大的脱靶量;③文献[16-19]虽考虑了控制受有界约束的情况,但只从攻击弹的角度出发对制导问题进行研究,文献[16-17]只分析了攻击弹采取先逃逸后追踪策略时能够命中飞行器的条件,文献[18-19]也只讨论并设计了攻击弹的制导律,并未对飞行器和防御弹的对策条件进行分析。
鉴于上述情况,本文基于微分对策理论对控制有界情况下的三方追逃问题进行了分析,基于范数型的性能指标为对策各方提出了不会导致加速度饱和的最优制导策略,然后从防守方(飞行器和防御弹)的角度出发,对攻击弹采取不同策略时飞行器能够成功逃离攻击弹的机动条件(不严格依赖防御弹)和防御弹能够成功拦截攻击弹的机动条件分别进行了分析和推导。
1 问题描述与运动学建模 1.1 协同追逃对策问题本文主要研究一个飞行器(目标)T受到一枚攻击弹M的威胁后发射一枚防御弹D进行防御的制导问题,考虑对策三方的侧向加速度均有界,并在制导律的推导过程中做出以下假设:
1) 对策三方在运动中均可视为质点,且速度均为常值。
2) 对策三方之间的相对运动可在初始视线方向附近线性化。
3) 重力因素可忽略,且制导问题可以在俯仰平面和偏航平面内解耦。
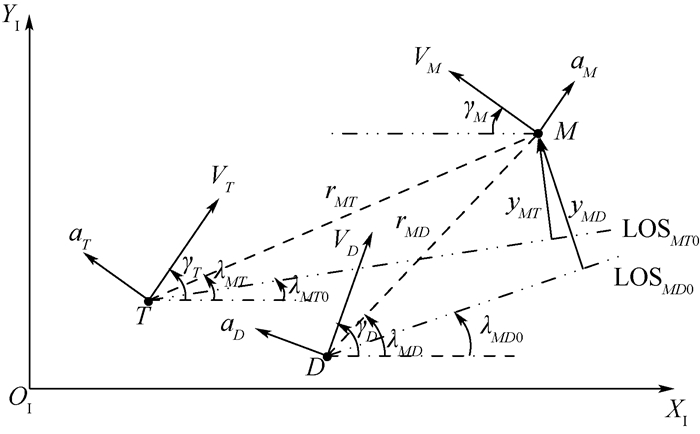
基于以上假设,本文主要在偏航平面内对制导问题进行研究,研究结论可以推广到三维情形。图 1所示为笛卡儿惯性坐标系下末制导段三方的平面相对运动关系。图中:V、a和γ分别为速度、侧向加速度和航向角;rMT和λMT分别为飞行器与攻击弹之间的距离和视线角;rMD和λMD分别为防御弹与攻击弹之间的距离和视线角;yMT为飞行器与攻击弹在垂直于初始视线LOSMT0方向上的距离;yMD为防御弹与攻击弹在垂直于初始视线LOSMD0方向上的距离。下标T、D和M分别表示飞行器、防御弹和攻击弹,数字0表示相应的初值。
|
| 图 1 对策三方的平面相对运动关系 Fig. 1 Relative in-plane movement relationship of three players |
由图 1可得极坐标下飞行器与攻击弹之间的相对运动方程为
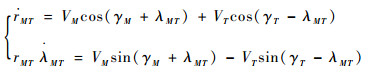
|
(1) |
类似可得防御弹与攻击弹之间的相对运动方程为

|
(2) |
式中: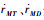
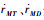
飞行器、防御弹和攻击弹各自的线性动力学方程为
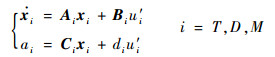
|
(3) |
式中:xi为三方各自的内部状态向量;u′i为其控制指令。假设三方的控制系统均具有理想动态特性,则有Ai=0,Bi=0,Ci=0,di=1,相应的加速度指令u′i=ai。
三方的航向角速度可表示为
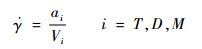
|
(4) |
将飞行器、防御弹和攻击弹的最大加速度指令记为uimax(i=T, D, M),则其控制指令应满足:
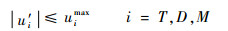
|
(5) |
将飞行器在垂直于LOSMT0方向上的加速度记为uTN,攻击弹在垂直于LOSMT0方向上的加速度记为uMN,防御弹在垂直于LOSMD0方向上的加速度记为uDN,则可得
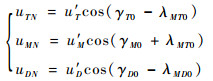
|
(6) |
根据假设2),飞行器、防御弹和攻击弹的对策时间(即飞行时间)可近似表示为
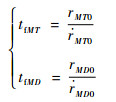
|
(7) |
式中:tfMT为飞行器与攻击弹的对策时间;tfMD为防御弹与攻击弹的对策时间。在后面的非线性仿真中,飞行时间将根据式(7)进行实时更新。
由于飞行器希望自身被攻击弹命中之前防御弹便对攻击弹实施拦截,故对策时间应满足tfMT>tfMD,可记Δt=tfMT-tfMD。又由于防御弹和攻击弹的距离在t=tfMD时刻达到最小(此即防御弹的脱靶量),当t>tfMD时防御弹和攻击弹之间的距离开始变大,防御弹已无法再对攻击弹形成威胁,它也不能再对飞行器和攻击弹的对策局势产生影响。故可规定在tfMD<t≤tfMT时间内防御弹不再存在,其存在函数可用l(t)表示:
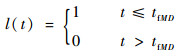
|
(8) |
则在对策中防御弹的加速度分量uDN可表示为
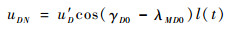
|
(9) |
将上述对策问题的状态向量取为
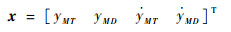
|
(10) |
记uT=uTN,uD=uDN,uM=uMN,则系统在垂直于初始视线方向上的运动方程可写为
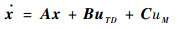
|
(11) |
式中:
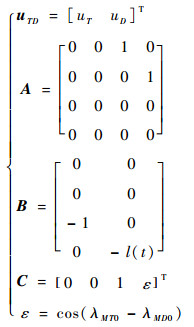
|
因为防御弹为飞行器所发射,所以一般有ε=1。
利用类似于文献[8]提到的所谓终端投影的系统降阶方法,引入新的变量——零控脱靶量(Zero Effort Miss, ZEM):
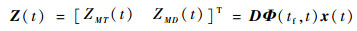
|
(12) |
式中:
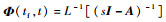
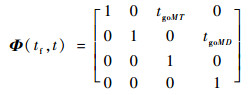
|
(13) |
式中:tgoMT为飞行器和攻击弹之间的剩余对策时间;tgoMD为防御弹和攻击弹之间的剩余对策时间。
经过式(12)的变换之后可得2个零控脱靶量:
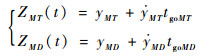
|
(14) |
将零控脱靶量作为新的状态变量,并求其关于时间的导数,可得新的状态方程为
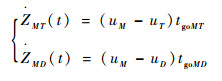
|
(15) |
在对策过程中,对于飞行器和防御弹组成的防守方来说,总是希望攻击弹的脱靶量yMT(tfMT)达到最大,同时希望防御弹的脱靶量yMD(tfMD)达到最小;而对策的另一方攻击弹其目的则完全相反,既希望yMD(tfMD)达到最大,又希望yMT(tfMT)达到最小。据此可选取2个脱靶量的绝对值之差作为对策问题的性能指标:

|
(16) |
由于脱靶量的绝对值属于范数的范畴,此类微分对策问题又被称为范数型微分对策(Norm Differential Game, NDG)[20]。
对策三方所进行的最优化问题可描述为
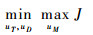
|
利用零控脱靶量可将性能指标式(16)改写为
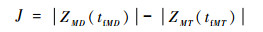
|
(17) |
该最优问题的哈密顿函数为

|
(18) |
式中:ηMT、ηMD为伴随状态。
最优问题的伴随方程和横截条件分别为

|
(19) |

|
(20) |
则进一步可得伴随状态为
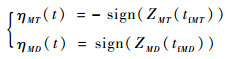
|
(21) |
根据最优控制的极小极大值原理,飞行器、防御弹和攻击弹的最优控制应满足:
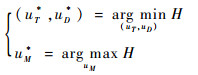
|
(22) |
结合式(15)和式(18)可得最优制导策略为
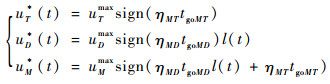
|
(23) |
由于tgoMT≥0,tgoMD≥0,利用式(21)并将最优制导策略进一步写成闭环形式可得
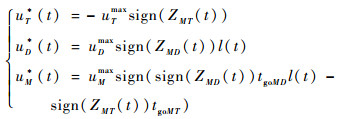
|
(24) |
飞行器与攻击弹进行一对一追逃对策时,易得其最优动力学为
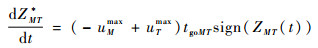
|
(25) |
对式(25)从0到t积分可得飞行器-攻击弹的最优对策轨迹为
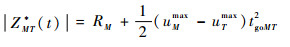
|
(26) |
式中: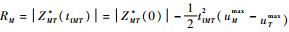
在本文所讨论的问题中,相较于攻击弹而言,一般有uTmax≤uMmax,故根据式(26)可得飞行器-攻击弹的对策空间如图 2所示。图中加粗的单调曲线ZMT*和-ZMT*表示攻击弹最终脱靶量为零的最优对策轨迹,2条曲线之间的区域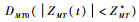
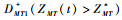
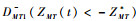
|
| 图 2 飞行器-攻击弹的对策空间 Fig. 2 Aircraft-attacking missile game space |
防御弹与攻击弹进行一对一追逃对策时,易得其最优动力学为

|
(27) |
对式(27)从0到t积分可得防御弹-攻击弹的最优对策轨迹为
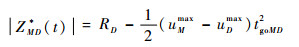
|
(28) |
式中: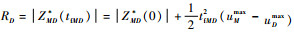
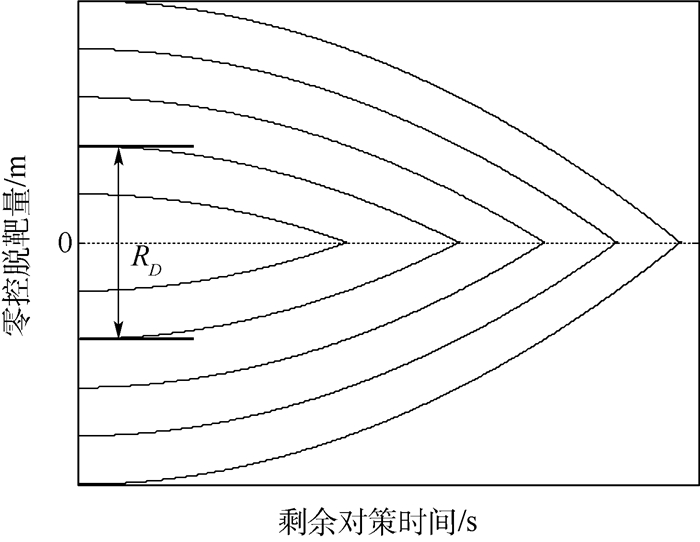
对于防御弹和攻击弹而言:①若uDmax≥uMmax,根据式(28)可得二者的对策空间与图 2相似,其分析也类似,不再赘述。②若uDmax<uMmax,则二者的对策空间如图 3所示,最优对策轨迹的值|ZMD*|随着时间t单调增加,最终脱靶量趋于ZMD*(tfMD),若防御弹在某一时刻t(t<tfMD)使得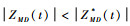
|
| 图 3 防御弹-攻击弹的对策空间(uDmax<uMmax) Fig. 3 Defender-attacting missile game space (uDmax < uMmax) |
本节根据2.1节推得的最优制导策略式(24)对三方的对策情况进行分析,并根据攻击弹的不同机动情况对飞行器实现逃逸和防御弹实现拦截的条件进行推导。这里假设对策三方的最大加速度指令满足不等式uTmax≤uDmax≤uMmax。
将式(24)代入式(15)可得系统最优动力学方程为
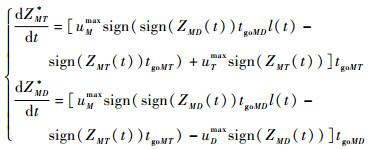
|
(29) |
最优动力学方程(29)中均包含了2个零控脱靶量的符号函数,下面根据符号函数sign(ZMT(t))、sign(ZMD(t))分2种情况进行分析。
1) 情况1
sign(ZMD(t))=-sign(ZMT(t))。此时飞行器、防御弹与攻击弹的视线角速度
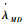

|
(30) |
式中:uMe*(t)表示攻击弹的最优逃逸策略;uMp*(t)表示攻击弹的最优追踪策略。
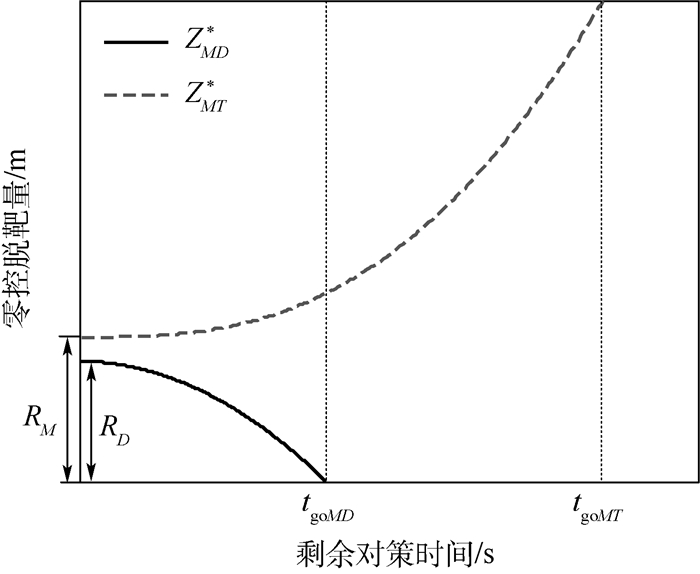
将式(30)代入式(29),并分别从0到t积分,可得2个最优对策轨迹依然如式(26)和式(28)所示。从式(30)也可看出,此时攻击弹的最优逃逸策略与最优追踪策略相同,这种情况下的最优对策只跟对策各方的初始条件有关,初始条件确定后各方的最优对策轨迹便随之确定,飞行器和防御弹只能采取各自的最优策略来应对,因而此种情况是非常简单的。根据式(26)和式(28)可得此时零控脱靶量如图 4所示。
|
| 图 4 2个零控脱靶量异号时的变化 Fig. 4 Evolution of two ZEM in case of opposite signs |
2) 情况2
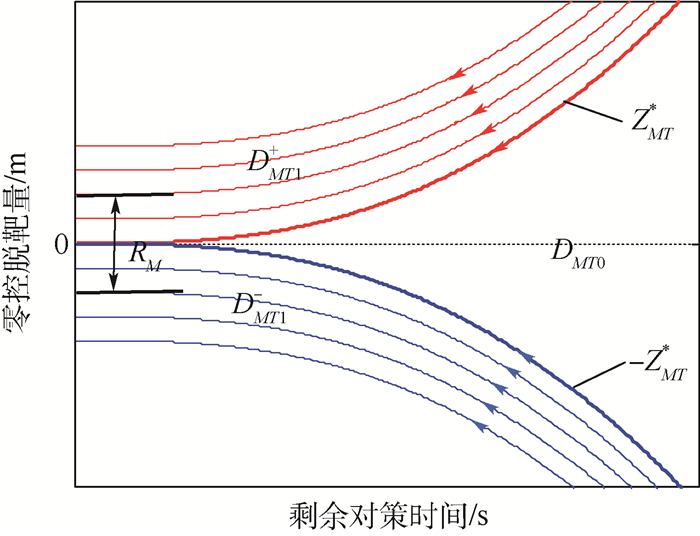
sign(ZMT(t))=sign(ZMD(t))。此时2个视线角速度
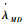
① 攻击弹首先采用最优逃逸策略而忽略对飞行器的拦截。此时攻击弹的制导策略为
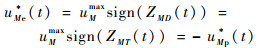
|
(31) |
此时攻击弹的制导策略与其最优追踪策略是完全相反的策略,若飞行器和防御弹均采用各自的最优策略,将式(31)代入式(29)并分别从0到t积分则可得三方的对策轨迹为

|
(32) |
根据式(32)第1式可得零控脱靶量同号时飞行器-攻击弹的对策轨迹如图 5中的点线所示。由图 5可以看出,由于攻击弹首先采用逃逸策略,其目的是逃脱防御弹的拦截而忽略了飞行器,导致其对飞行器的脱靶量将随着时间增大。如果攻击弹与飞行器之间的零控脱靶量在某一时刻t′(t′<tfMD)满足|ZMT**(t′)|>|ZMT*(t′)|,根据2.2.1节的分析可知,即便攻击弹再切换成最优追踪策略,飞行器已经不在飞行器-攻击弹最优对策的捕获区内,飞行器采用最优逃逸策略时仍能够以脱靶量|ZMT**(tfMT)|>RM结束与攻击弹的对抗,从而成功逃离攻击弹。

|
| 图 5 攻击弹首先采用最优逃逸策略时的零控脱靶量 Fig. 5 Evolution of ZEM while attacking missile performs optimal evasion first |
在攻击弹与防御弹进行最优逃逸-追踪对策的同时,飞行器以uT(t)=-uTmaxsign(zMT(t))进行最优逃逸机动,若在推导式(32)第1式时进行一些代数运算则可得
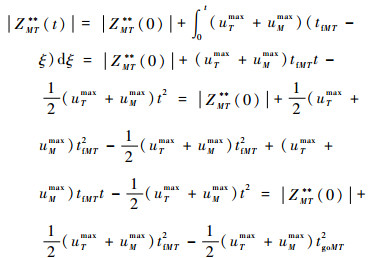
|
(33) |
式中:|ZMT**(0)|为初始时刻(t=0)的飞行器-攻击弹零控脱靶量。
再结合2.2.1节的分析可知,零控脱靶量式(33)与最优对策轨迹式(26)应有下列不等式关系成立:
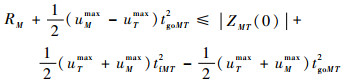
|
(34) |
整理可得
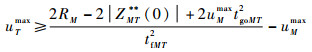
|
(35) |
又因为式(34)最晚应在t=tfMD时刻成立(此时tgoMT=tfMT-tfMD=Δt),故uTmax应满足:
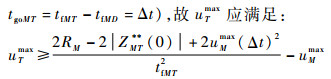
|
(36) |
式(36)即为飞行器的最大加速度指令应满足的最小逃逸机动条件。
② 攻击弹直接采用最优追踪策略而忽略对防御弹的躲避。此时攻击弹的制导策略为
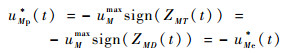
|
(37) |
此时攻击弹的制导策略与其最优逃逸策略是完全相反的策略,若飞行器和防御弹均采用其最优策略,将式(37)代入式(29)并分别从0到t积分可得三方的对策轨迹为
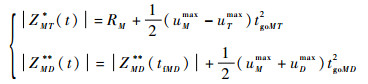
|
(38) |
根据式(38)第2式可得防御弹-攻击弹的最优对策轨迹如图 6中的点线所示。由于攻击弹首先采用的是追踪策略,其目的是对飞行器进行拦截而忽略了对防御弹的躲避,此时其与防御弹之间的脱靶量也将随着时间而减小。如果攻击弹在捕获飞行器之前的某一时刻t′(t′<tfMD)与防御弹之间的零控脱靶量满足|ZMD**(t′)|<|ZMD*(t′)|,则根据2.2.2节的分析可知,防御弹采用其最优追踪策略时就能够以脱靶量|ZMD**(tfMD)|<RD结束与攻击弹的对抗,从而成功拦截攻击弹。

|
| 图 6 攻击弹直接采用最优追踪策略时的零控脱靶量 Fig. 6 Evolution of ZEM while attacking missile performs optimal pursuit directly |
在攻击弹与飞行器进行最优追踪-逃逸对策的同时,防御弹以uD(t)=uDmaxsign(ZMD(t))对攻击弹进行最优追踪机动,若在推导式(38)第2式时进行一些代数运算则可得到:
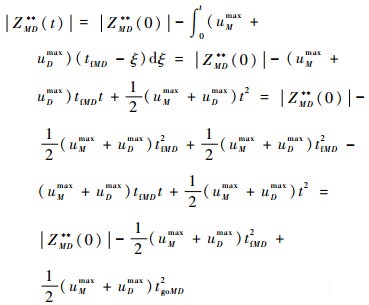
|
(39) |
式中:|ZMD**(0)|为初始时刻(t=0)的防御弹-攻击弹零控脱靶量。
再结合2.2.2节的分析可知,零控脱靶量式(39)与最优对策轨迹式(28)应有下列不等式关系成立:
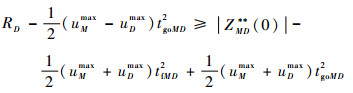
|
(40) |
整理可得

|
(41) |
又因为式(40)最晚应在t=tfMD时刻成立(此时tgoMD=0),故可得
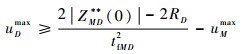
|
(42) |
式(42)即为防御弹的最大加速度指令应满足的最小拦截机动条件。
4 仿真验证本节基于非线性仿真对2.1节推导的制导律及第3节的分析进行验证。由于零控脱靶量ZMT和ZMD异号的情况对于飞行器和防御弹来说是最简单的情况,故仿真的主要内容为第3节中sign(ZMT(t))=sign(ZMD(t))的情况。假设防御弹对攻击弹的脱靶量小于10 m时即认为攻击弹被拦截(RD=10 m),攻击弹对飞行器的脱靶量小于10 m时即认为飞行器被命中(RM=10 m)。
4.1 攻击弹首先采用最优逃逸策略此时攻击弹先采用式(31)所示的逃逸策略,逃脱之后再切换成式(37)所示的追踪策略拦截飞行器,而飞行器和防御弹的制导策略分别如式(24)第1式和第2式所示,其他相关仿真参数如表 1所示。
| 仿真参数 | 飞行器 | 防御弹 | 攻击弹 |
| 初始位置/m | (0, 0) | (0, 0) | (9 000, -200) |
| 初始航向/(°) | 60 | 20 | 0 |
| 速度/(m·s-1) | 300 | 800 | 700 |
为了验证飞行器能否逃离攻击弹,在仿真中应根据所给参数由式(36)进行实时判断。
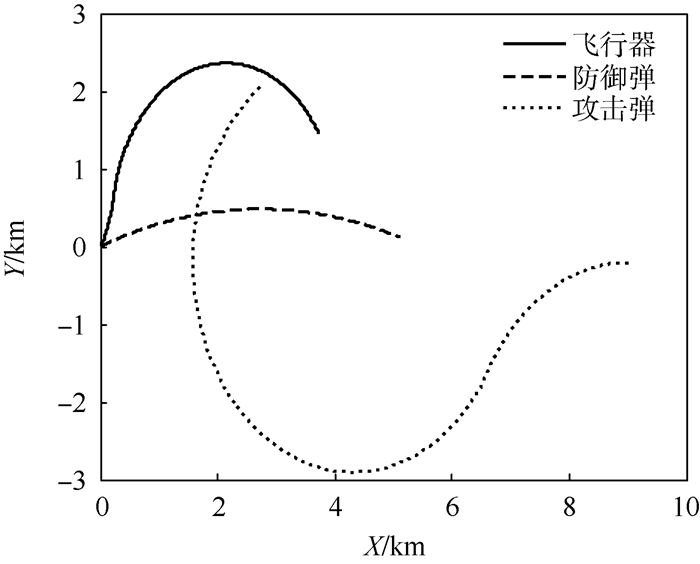
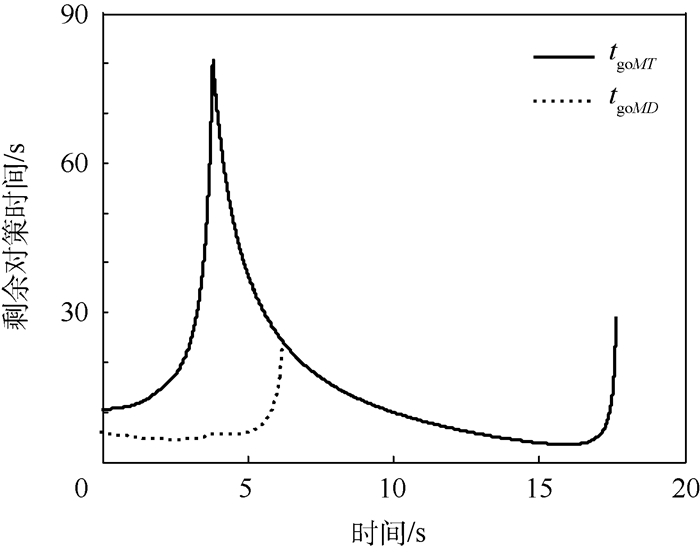
1) 假设飞行器、防御弹和攻击弹的最大加速度指令分别为uTmax=50 m/s2、uDmax=80 m/s2和uMmax=180 m/s2。基于上述参数,在仿真中可以发现飞行器的控制指令满足式(36)的约束,此时三方的运动轨迹如图 7所示。从图 7可以明显看出,当飞行器的最大加速度指令满足最小机动条件时可以成功逃脱攻击弹,飞行器并不严格依赖于防御弹提前将攻击弹拦截。这一点与文献[8]不同,该文中当飞行器速度小于攻击弹速度时,飞行器始终会被攻击弹命中,飞行器严格依赖防御弹的存在。图 8为2个剩余对策时间随时间变化的示意图。可以看出,由于攻击弹先采用逃逸策略,剩余对策时间tgoMT与时间t已完全不是线性的关系,即使攻击弹切换成最优追踪策略,由于飞行器满足实现逃逸的最小机动条件,新的碰撞三角形无法建立,tgoMT与时间t仍然不具有线性关系。
|
| 图 7 攻击弹首先逃逸时的三方运动轨迹(uTmax大于其最小逃逸机动) Fig. 7 Trajectories of three players while attacking missile evades first (uTmaxis larger than minimal evasion maneuver) |
|
| 图 8 攻击弹首先逃逸时2个剩余对策时间的变化(uTmax大于其最小逃逸机动) Fig. 8 Evolution of two time-to-go while attacking missile evades first (uTmax is larger than minimal evasion maneuver) |
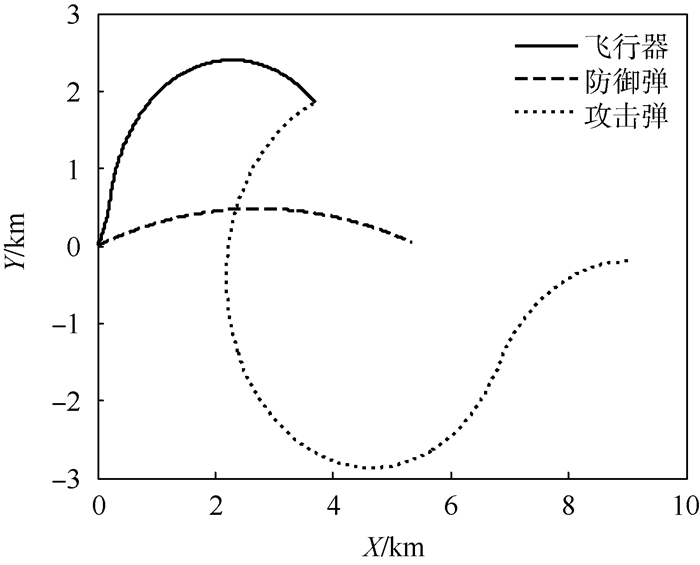
2) 假设飞行器、防御弹和攻击弹的最大加速度指令分别为uTmax=50 m/s2、uDmax=80 m/s2和uMmax=200 m/s2。基于上述参数,在仿真过程中可以发现飞行器的控制指令不满足式(36)的约束,此时三方的运动轨迹如图 9所示。从图 9可以看出,由于攻击弹的最大加速度指令增大,导致飞行器的最大加速度不满足式(36)所示的最小机动条件,使得飞行器不能逃脱攻击弹的拦截(攻击弹对飞行器最终的脱靶量为yMT=4.481 m<RM)。
|
| 图 9 攻击弹首先逃逸时的三方运动轨迹(uTmax小于其最小逃逸机动) Fig. 9 Trajectories of three players while attacking missile evades first (uTmax is smaller than minimal evasion maneuver) |
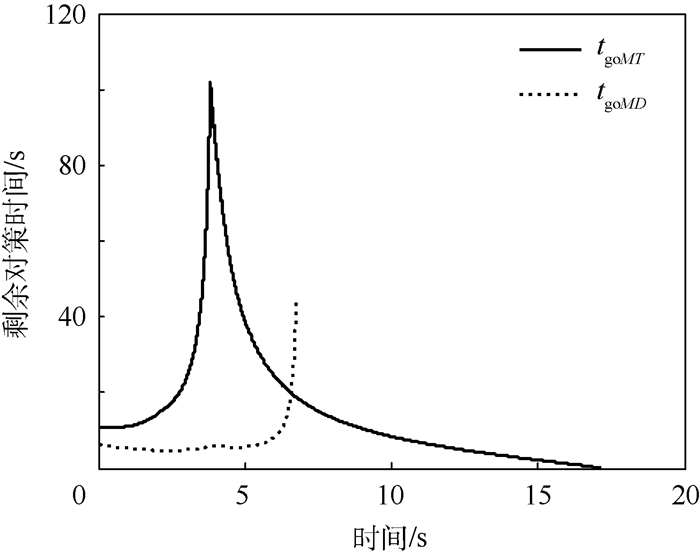
图 10所示为2个剩余对策时间随时间的变化关系。由图中可以看出,由于飞行器不满足实现逃逸的最小机动条件,虽然在对策初期tgoMT与时间t不具有线性关系,但经过一段时间的过渡之后建立了新的碰撞三角形,从而有了近似的线性关系,最终飞行器逃逸失败。
|
| 图 10 攻击弹首先逃逸时2个剩余对策时间的变化(uTmax小于其最小逃逸机动) Fig. 10 Evolution of two time-to-go while attacking missile evades first (uTmax is smaller than minimal evasion maneuver) |
此时攻击弹只采用如式(37)所示的追踪策略,飞行器和防御弹的制导策略仍如式(24)所示,三方的其他相关参数如表 2所示。
| 仿真参数 | 飞行器 | 防御弹 | 攻击弹 |
| 初始位置/m | (0, 0) | (0, 0) | (3 000, -200) |
| 初始航向/(°) | 12 | 7 | 0 |
| 速度/(m·s-1) | 300 | 800 | 700 |
为了验证防御弹能否拦截攻击弹,在仿真中应根据所给参数由式(42)进行实时判断。
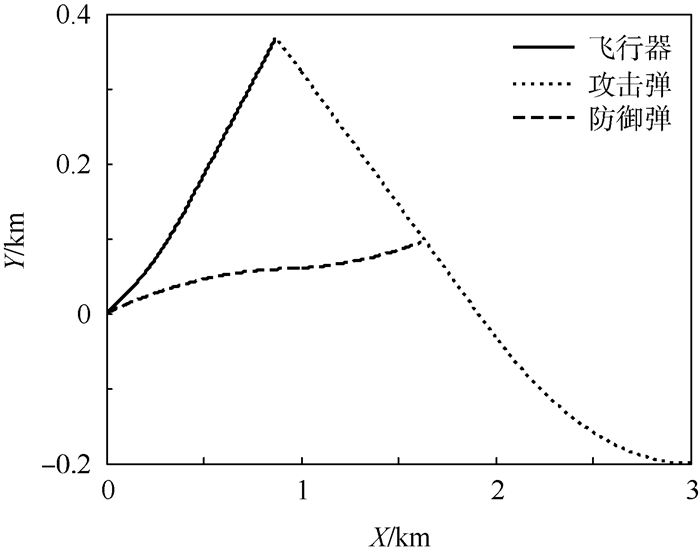
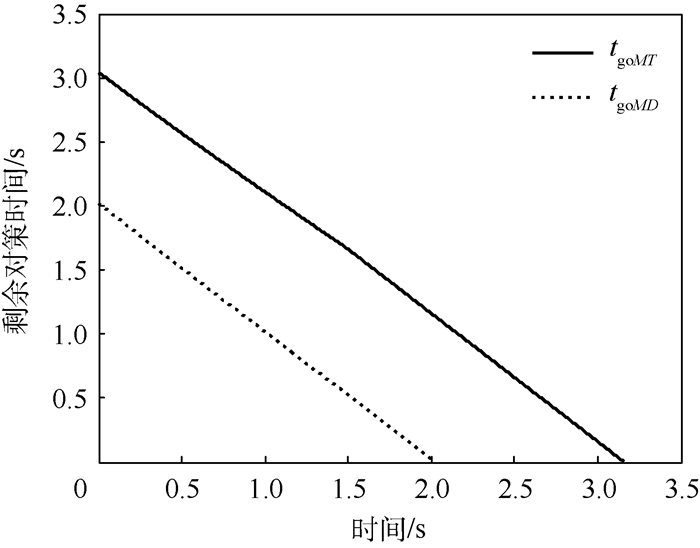
1) 假设飞行器、防御弹和攻击弹的最大加速度指令分别为uTmax=50 m/s2、uDmax=80 m/s2和uMmax=160 m/s2。基于上述参数,在仿真过程中可以发现防御弹的加速度指令满足式(42)的约束,此时三方的运动轨迹如图 11所示。从图 11可以看出,防御弹在攻击弹命中飞行器之前成功将攻击弹拦截(脱靶量为yMD=5.902 m<RD)。图 12为2个剩余对策时间随时间变化的示意图。可以看出,2个剩余对策时间与时间几乎呈线性关系,而剩余对策时间tgoMD小于tgoMT,防御弹在攻击弹命中飞行器之前对其实施了拦截。
|
| 图 11 攻击弹直接追踪时的三方运动轨迹(uDmax大于其最小拦截机动) Fig. 11 Trajectories of three players while attacking missile pursues directly (uDmax is larger than minimal interception maneuver) |
|
| 图 12 攻击弹直接追踪时2个剩余对策时间的变化(uDmax大于其最小拦截机动) Fig. 12 Evolution of two time-to-go while attacking missile pursues directly (uDmax is larger than minimal interception maneuver) |
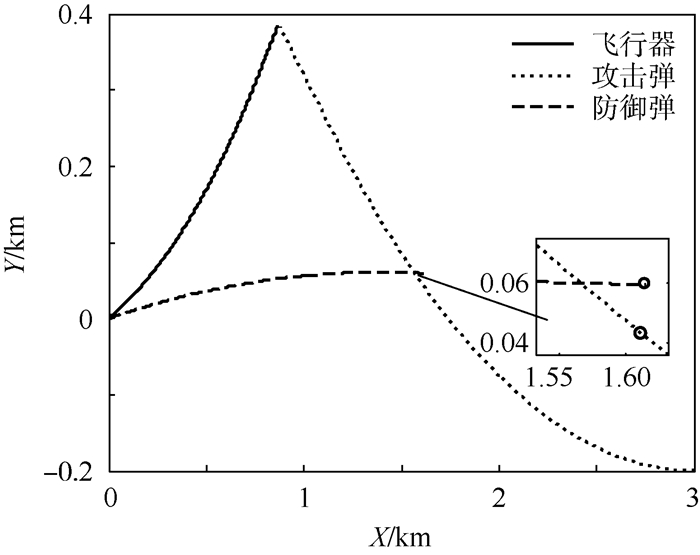
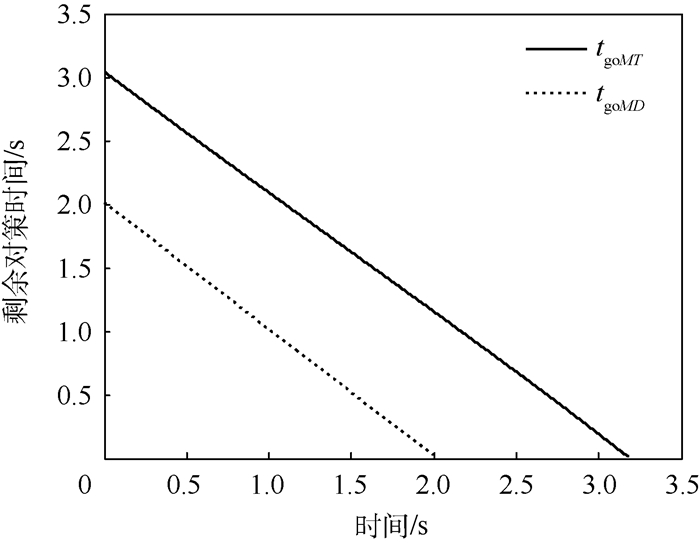
2) 假设飞行器、防御弹和攻击弹的最大加速度指令分别为uTmax=40 m/s2、uDmax=40 m/s2和uMmax=120 m/s2。基于上述参数,在仿真过程中可以发现防御弹的加速度指令不满足式(42)的约束,此时三方的运动轨迹如图 13所示。可以看出,防御弹未能在攻击弹命中飞行器之前将其拦截(防御弹对攻击弹脱靶量为yMD=15.199 m>RD)。图 14为2个剩余对策时间与时间的变化关系。
|
| 图 13 攻击弹直接追踪时的三方运动轨迹(uDmax小于其最小拦截机动) Fig. 13 Trajectories of three players while attacking missile pursues directly (uDmax is smaller than minimal interception maneuver) |
|
| 图 14 攻击弹直接追踪时2个剩余对策时间的变化(uDmax小于其最小拦截机动) Fig. 14 Evolution of two time-to-go while attacking missile pursues directly (uDmax is smaller than minimal interception maneuver) |
1) 针对具有主动防御能力的飞行器面对来袭导弹发射一枚防御弹进行防御的制导问题,给出了一种基于范数型性能指标的最优制导律。
2) 对攻击弹采用不同制导策略的情况,分别推导了飞行器能够逃离攻击弹和防御弹能够拦截攻击弹的条件。
3) 攻击弹采取先逃逸后追踪的策略时,飞行器若满足其最小逃逸机动条件则可逃脱攻击弹的拦截,否则飞行器将被攻击弹拦截。
4) 攻击弹直接采取追踪策略时,防御弹若满足其最小拦截机动条件则可拦截攻击弹,否则防御弹将无法在飞行器被命中前将攻击弹拦截。
| [1] |
SHAFERMAN V, SHIMA T. Cooperative multiple-model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(6): 1801-1813. DOI:10.2514/1.49515 |
| [2] |
SHIMA T. Optimal cooperative pursuit and evasion strategies against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 414-425. DOI:10.2514/1.51765 |
| [3] |
PROKOPOV O, SHIMA T. Linear quadratic optimal cooperative strategies for active aircraft protection[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 753-764. DOI:10.2514/1.58531 |
| [4] |
RATNOO A, SHIMA T. Line-of-sight interceptor guidance for defending an aircraft[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 522-532. DOI:10.2514/1.50572 |
| [5] |
YAMASAKI T, BALAKRISHNAN S N, TAKANO H. Modified command to line-of-sight intercept guidance for aircraft defense[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 898-902. DOI:10.2514/1.58566 |
| [6] |
RATNOO A, SHIMA T. Guidance strategies against defended aerial targets[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1059-1068. DOI:10.2514/1.56924 |
| [7] |
BOYELL R L. Defending a moving target against missile or torpedo attack[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(4): 522-526. |
| [8] |
PERELMAN A, SHIMA T, RUSNAK I. Cooperative differential games strategies for active aircraft protection from a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 761-773. DOI:10.2514/1.51611 |
| [9] |
GARCIA E, CASBEER D W, PACHTER M. Cooperative strategies for optimal aircraft defense from an attacking missile[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1510-1520. DOI:10.2514/1.G001083 |
| [10] |
GARCIA E, CASBEER D W, PACHTER M. Active target defense differential game:Fast defender case[J]. IET Control Theory and Applications, 2017, 11(17): 2985-2993. DOI:10.1049/iet-cta.2017.0302 |
| [11] |
GARCIA E, CASBEER D W, FUCHS C Z, et al. Cooperative missile guidance for active defense of air vehicles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(2): 706-721. DOI:10.1109/TAES.2017.2764269 |
| [12] |
PACHTER M, GARCIA E, CASBEER D W.Active target defense differential game[C]//52nd Annual Allerton Conference on Communication, Control, and Computing.Piscataway, NJ: IEEE Press, 2014: 46-53.
|
| [13] |
RUSNAK I. The lady, the bandits and the body-guard game[C]//The 44th Israel Annual Conference on Aerospace Sciences.Haifa: Israel Institute of Technology, 2004: 25-26.
|
| [14] |
RUSNAK I.The lady, the bandits and the body guards-A two team dynamic game[C]//Proceedings of the 16th World IFAC Congress.Prague: IFAC, 2005: 441-446.
|
| [15] |
RUSNAK I.Games based guidance in anti-missile defense for high order participants[C]//Proceeding of the 15th IEEE Mediterranean Electrotechnical Conference.Piscataway, NJ: IEEE Press, 2010: 812-817.
|
| [16] |
RUBINSKY S, GUTMAN S.Three body guaranteed pursuit and evasion: AIAA-2012-4910[R].Reston: AIAA, 2012.
|
| [17] |
RUBINSKY S, GUTMAN S. Three-player pursuit and evasion conflict[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(1): 98-110. DOI:10.2514/1.61832 |
| [18] |
孙启龙, 齐乃明, 赵钧, 等. 攻击主动防御飞行器的微分对策制导律[J]. 国防科技大学学报, 2018, 40(3): 7-14. SUN Q L, QI N M, ZHAO J, et al. Differential game guidance laws against active defense aircraft[J]. Journal of National University of Defense Technology, 2018, 40(3): 7-17. (in Chinese) |
| [19] |
SUN Q L, QI N M, XIAO L X, et al. Differential game strategy in three-player evasion and pursuit scenarios[J]. Journal of Systems Engineering and Electronics, 2018, 29(2): 352-366. DOI:10.21629/JSEE.2018.02.16 |
| [20] |
TURETSKY V, SHINAR J. Missile guidance laws based on pursuit-evasion game formulations[J]. Automatica, 2003, 39(4): 607-618. DOI:10.1016/S0005-1098(02)00273-X |



