逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像具有全天时、全天候、远距离、高分辨等特点,其能够提供丰富的目标结构信息。利用ISAR进行空间目标成像是空间态势感知的重要内容,是夺取未来空天优势的重要保障。但是由于各种干扰因素及噪声的存在,导致ISAR像的质量受损,难以直接用于图像特征提取及空间目标识别等应用。为了解决该问题,开展ISAR像的图像处理与改进显得尤为重要。文献[1]研究了ISAR像斑点噪声的去除方法,并利用分水岭法进行ISAR像分割;文献[2]针对ISAR像存在的低散斑噪声,使用线性滤波器及中值滤波器提高图像质量,并在图像质量严重受损时利用Lee滤波器替代中值滤波器;文献[3]研究了利用色散相拉伸变换对数字图像进行边缘检测的方法;文献[4]在数据不可用或严重受损的条件下提出利用梯度恢复算法对ISAR像进行分析与恢复;文献[5]针对雷达散射截面积(Radar Cross Section,RCS)数据丢失的情况,利用压缩感知算法生成目标的ISAR像,并利用极化映射方法提取了目标特征;文献[6]提出利用全局迭代阈值及局部散射点强度削减法分别对斑点噪声与横条纹干扰进行抑制,并通过形态学、邻域平均法及图像归一化处理最终实现了ISAR像的预处理。上述研究成果均可用于ISAR像的处理与改进,但是缺乏针对空间目标ISAR像实际问题(如内部空洞存在、轮廓线损坏等)的具体研究方案。
基于ISAR像的特征向量提取主要包括ISAR像数据生成、噪声抑制、边缘检测及轮廓特征提取等步骤。文献[7]研究了提取目标几何特征进行目标识别的方法;文献[8]提出了侧抑制神经网络算法在目标识别中的应用;文献[9]利用点目标仿真算法生成轨道目标的ISAR像,并通过提取尺寸等参数进行了目标识别;文献[10]研究了基于目标轮廓特征的分类器融合算法效果,并对4种融合算法的识别性能进行了对比分析;文献[11-12]提出了基于几何散列法的ISAR像自动识别方法及基于局部非负矩阵分解特征空间优化的ISAR像识别算法;文献[13]分别从目标微动特征、目标电磁特征等方面对ISAR像目标特征的提取方法展开了研究;文献[14]提出利用酉ESPRIT方法提取目标闭合轮廓线,为ISAR目标识别提供了更加稳定的特征;文献[15-17]针对ISAR像目标识别的特征提取与识别问题展开了深入研究。对于ISAR像特征向量尺度单一问题,文献[15]提出了一种基于直方图统计量的特征提取方法;文献[16]提出了一种基于分块双向二维投影梯度非负矩阵分解的特征向量提取方法,解决了特征提取过程中不允许负分解量存在的问题;文献[17]从融合角度出发,研究了ISAR像的Gabor特征,提出了一种基于Gabor小波变换幅值特征和相位特征相融合的ISAR像目标识别算法。
利用神经网络算法对空间目标进行识别时,需要确定目标在帧中的精确位置,解决该问题的方法之一在于利用目标轮廓线生成图像的矢量图,但由于实际情况中噪声干扰的存在,使得目标轮廓线模糊,增加了轮廓特征提取难度。对此,本文基于ISAR成像模型、ISAR信号模型及ISAR图像函数提取模型,设计了图像处理算法,该算法可以应用于不同目标的ISAR像。
1 ISAR成像模型、坐标转换及方位分辨率 1.1 ISAR成像模型建立ISAR的卫星观测坐标系Oxyz,卫星在观测坐标系Oxyz中以速度V运动。以卫星的几何中心为原点,建立卫星的本体坐标系O′XYZ,原点O′与卫星几何中心重合。在本体坐标系中建立卫星的三维网格模型,利用三维网格模型上均匀分布的节点描述卫星的几何特性,如图 1所示。

|
| 图 1 ISAR成像几何模型 Fig. 1 ISAR imaging geometry model |
N为卫星三维网格模型上的任一节点,当前ISAR到节点N的测量距离矢量为RN(p)=[xN(p), yN(p), zN(p)]T,其可由观测坐标系Oxyz的原点O到节点N的距离矢量表示:
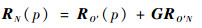
|
(1) |
式中:RO′(p)=[xO′(p), yO′(p), zO′(p)]为第p个脉冲时ISAR到卫星几何中心的距离矢量,由表达式RO′(p)=RO′(p-1)+V·T确定,p为发射的脉冲数,p∈{1, 2, …, M},M为发射的脉冲总数,T为脉冲重复周期,RO′(0)=[xO′(0), yO′(0), zO′(0)]为ISAR在第1个脉冲p=1时与卫星几何中心的距离矢量,V=[Vcos α, Vcos β, Vcos γ]为卫星的运动速度矢量,cos α、cos β、cos γ为速度矢量的方向余弦,且满足cos γ = 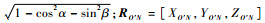
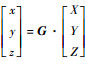
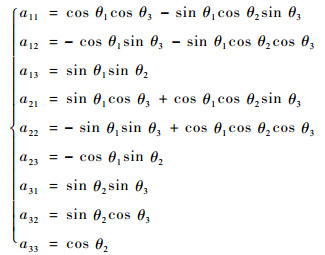
|
(2) |
其中:θ1、θ2、θ3的表达式为
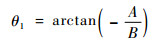
|
(3) |
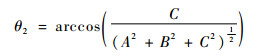
|
(4) |
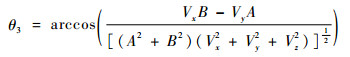
|
(5) |
式中:A、B、C分别为基准平面Q的法向量分量;Vx、Vy、Vz分别为卫星速度矢量的分量。该基准平面Q的定义为:过观测坐标系Oxyz原点O、卫星几何中心在第p次脉冲时位置O′(xO′(p), yO′(p), zO′(p))及第p次脉冲内卫星运动轨迹线方程所确定的平面。第p次脉冲内的卫星运动轨迹线方程可以表示为(ISAR的一个合成孔径时间为微秒级,因此在一个合成孔径时间内将卫星运动轨迹近似为直线运动)
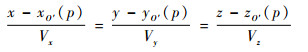
|
(6) |
其矩阵方程可描述为

|
(7) |
式(7)也可以写为
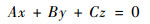
|
(8) |
式中:
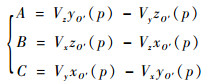
|
(9) |
因此,可以求得第N个散射点的位置矢量模型RN(p),在对ISAR线性调频信号建模时,可以利用其计算从卫星散射体反射信号的时间延迟。
1.2 ISAR成像几何转换从卫星上反射回来的ISAR信号,可以在二维跟踪坐标系中利用径向距离Yv和横向距离Xu进行描述,这就意味着卫星的三维几何被转换成在二维坐标系

在二维信号配准平面中,建立2个二维坐标系:坐标系OXuYv跟踪卫星的几何中心,坐标系O′Xu^Yv^与卫星本体固连(见图 2)。图 2中:坐标系OXuYv中,OYv轴沿OO′连线方向,OXu轴在基准平面Q内与OYv相垂直;坐标系O′Xu^Yv^中,O′Xu^轴与速度方向V相同,O′Yv^轴在基准平面Q内与O′Xu^轴垂直。

|
| 图 2 ISAR信号平面上的两个二维坐标系 Fig. 2 Two two-dimensional coordinate systems established on ISAR signal plane |
第N个散射点的坐标(Xu^v^, Yu^v^)可以由该点的位置矢量RO′N及坐标轴的单位方向矢量ex、ey表示:
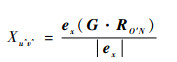
|
(10) |
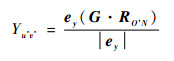
|
(11) |
式中: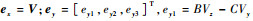
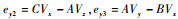
引入二维跟踪坐标系,卫星的运动轨迹被分解为几何中心O′沿OYv轴的平移及相对于几何中心O′的旋转。卫星几何中心平移后的位置矢量为RO′(p),卫星绕几何中心的旋转由本体坐标系O′Xu^Yv^相对于跟踪坐标系OXuYv的旋转定义。
坐标轴Yv与Yv^之间的旋转角度θ(p)可通过其方向矢量RO′(p)与ey内积的反余弦求得:
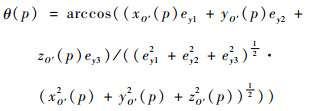
|
(12) |
在跟踪坐标系OXuYv中的第u^v^个散射点的位置矢量可以表示为
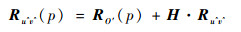
|
(13) |
式中:Ru^v^(p)=[Xu^v^(p), Yu^v^(p)]T为第u^v^个点的位置矢量;RO′(p)=[0, RO′(p)]T为卫星几何中心在坐标系OXuYv中的距离矢量;H= 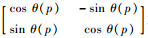
从式(13)中可以看出,卫星的运动被分解为卫星几何中心的径向平移RO′(p)=[0, RO′(p)]T和卫星绕其几何中心的旋转H·Ru^v^。
1.4 卫星的方位分辨率为了确定ISAR像在帧中的位置,在基准平面Q内建立静止二维观测坐标系Ox′y′,如图 3所示。

|
| 图 3 卫星在相平面中的位置及方位向分辨率 Fig. 3 Satellite position in imaging plane and azimuth resolution |
Ox′为基准平面Q与平面Oxy之间的交线,定义为:Ax+By+Cz=0,z=0,也可以表示为:x/B=-y/A。
根据坐标轴Oy′与Ox′及基准平面Q的正交性,可以求得Oy′的表达式为
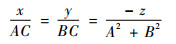
|
(14) |
坐标轴Ox′与速度矢量之间的夹角ϑ定义为
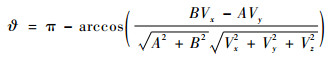
|
(15) |
由图 3可知,在一个合成孔径时间内,卫星从点O′运动到点D。雷达观测方向OO′与坐标轴Ox′之间的初始方位角Φ(0)为
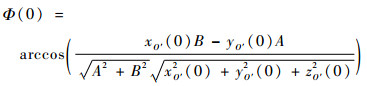
|
(16) |
当卫星运动到点D时,方位角Φ(p)为
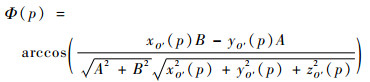
|
(17) |
点O′(0)为卫星几何中心在初始时刻的位置,OO′为雷达到卫星几何中心的初始观测方向。在图 3中,O′D与Ox′之间的夹角大小为ϑ,定义O′D为一个合成孔径长度,其值由合成孔径时间内的发射脉冲数np、脉冲发射周期及卫星运动速度确定:

|
(18) |
OO′与OD之间的夹角Ψ表示一个合成孔径长度对应的角度大小:
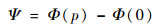
|
(19) |
径向分辨率由发射脉冲的带宽决定,为使方位分辨率等于径向分辨率,有必要定义合成孔径的长度大小或者单位合成孔径时间内的脉冲周期数np。方位分辨率大小由有效合成孔径长度计算得到,有效合成孔径长度O′B可以表示为
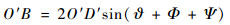
|
(20) |
基于衍射理论,发射波长为λ的雷达波的方位角分辨率大小为

|
(21) |
由此,计算得到雷达方位分辨率ΔL为
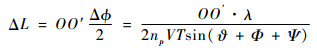
|
(22) |
实际中,雷达与卫星间距离为百公里量级,在一个合成孔径时间内,方位分辨率可近似为
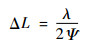
|
(23) |
为了实现特定的方位分辨率,由式(22)可以求得一个合成孔径周期内的脉冲数np为
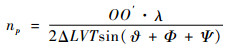
|
(24) |
在球面波的传播条件下,卫星反射的线性调频信号可以表示为
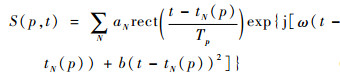
|
(25) |
式中:
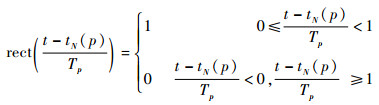
|
(26) |
其中:aN为卫星上第N个散射点的后向散射系数;Tp为线性调频信号脉冲宽度;ω=2πc/λ为载波角频率,雷达波的传播速度为c=3×108 m/s;b=πΔF/Tp,ΔF/Tp线性调频信号的调频率,ΔF为带宽;tN(p)=2RN(p)/c为信号从第N个散射点返回的时间延迟,RN(p)为雷达到散射点N的距离大小;t=tNmin(p)+kΔT为径向测量的快时间,k∈{1, 2, …, K}为线性调频信号的采样数,K=T/ΔT为信号样本的总数量,ΔT为样本的采样周期,tNmin(p)=2RNmin(p)/c为从卫星最近散射点反射ISAR信号的最小时间延迟。
在式(25)的两侧分别乘以发射波形的复共轭波形exp[-j(ωt+bt2)],得到解调后的ISAR信号为
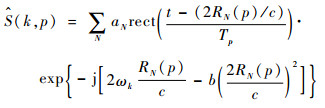
|
(27) |
式中: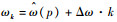
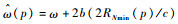
从式(27)中可以看出,三维图像函数aN被转化成二维信号函数。通过对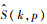
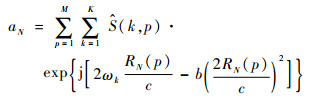
|
(28) |
式(28)可以视为卫星所有散射点的相位补偿过程。因此,ISAR成像属于一种全运动补偿。其中,指数项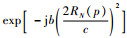
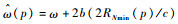
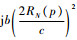
在将三维ISAR信号转换到二维信号平面并忽略掉二次项以后,式(28)可以重写为
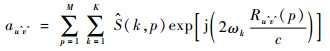
|
(29) |
式中:信号平面上散射点的离散坐标取值范围为:u^∈{1, 2, …, M},v^∈{1, 2, …, K}。即在图像重构过程中,方位向u^和径向v^的像素个数分别等于发射脉冲数p及每个脉冲内的采样数k。
在雷达反射波近似为平面波的情况下,雷达到任意散射点u^v^的距离Ru^v^(p)可以等效为径向距离,因此Ru^v^(p)可以表示为
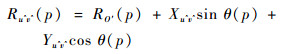
|
(30) |
表达式(29)可以重新写为
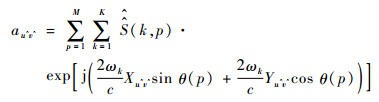
|
(31) |
式中: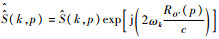
指数项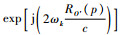
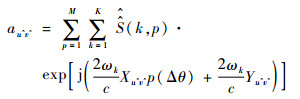
|
(32) |
在补偿完卫星几何中心的二阶运动及径向位移之后,可以通过二维傅里叶变换提取复成像函数。

|
(33) |
式中:

本质上,式(33)是一个自优化过程,使位于离散坐标区间u^∈{1, 2, …, M},v^∈{1, 2, …, K}内的散射点强度值最大。脉内傅里叶变换实现距离压缩,脉间傅里叶变换实现相位补偿。
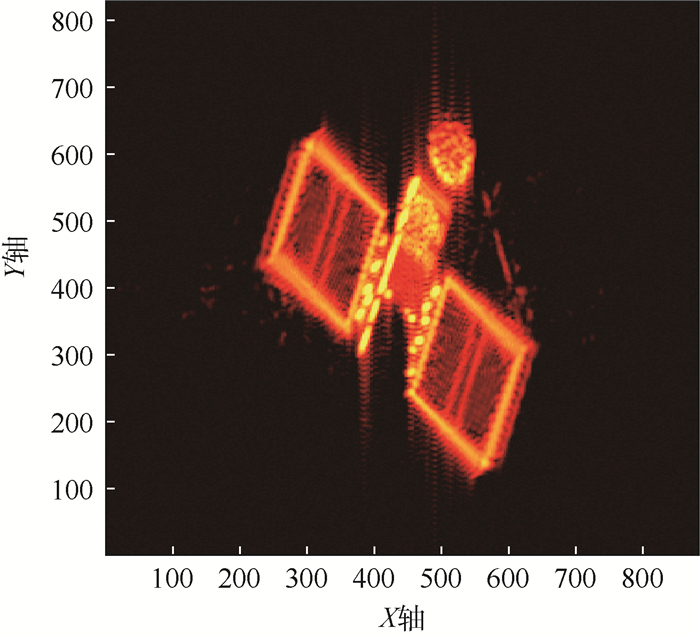
3 ISAR像处理 3.1 ISAR成像仿真首先建立卫星的三维网格模型,网格单元大小为ΔX=0.1 m,ΔY=0.1 m,ΔZ=0.1 m。卫星在788.9 km的圆轨道运行,轨道倾角为98.57°,升交点赤经为99.44°,近地点幅角为90°。ISAR所在位置为东经119°,北纬29.5°。ISAR发射线性调频信号照射卫星,参数为:载波频率fc=10 GHz,角频率ω=2πfc,周期T=1/fc,波长λ=c/fc,频率带宽ΔF=1 GHz,脉冲宽度Tp=1×10-5 s,调频率为ΔF/Tp,采样率fs=1×107 Hz,采样周期ΔT=1/fs。利用式(25)生成卫星回波数据,利用式(33)进行卫星图像提取,并通过旁瓣抑制及相干斑滤波对图像进行初步处理,得到卫星的ISAR仿真图像,如图 4所示。
|
| 图 4 目标卫星的ISAR仿真图像 Fig. 4 Simulated ISAR image of target satellite |
实际过程中,卫星在ISAR像中的位置取决于卫星的运动参数及其所处的空间位置,这导致了卫星在ISAR像中的位置及指向是任意分布的,增加了图像识别的难度。因此,有必要对ISAR像进行旋转处理,使目标卫星的纵轴(最长轴)与像平面的横轴平行。旋转校正首先需要将目标卫星从背景中分离,其次检测出目标卫星最长轴,最后将最长轴旋转至与像平面的横轴平行。
3.2.1 ISAR像的二值化处理为了将卫星从背景中分离,本文采用大津法(Otsu)进行最佳阈值确定,该方法的原理是通过最大类间方差进行阈值的自适应确定。
将ISAR灰度图的灰度值大小表示为[0, 1, …, 255],且每个灰度值对应的像素个数为ni,总的像素个数为
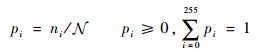
|
(34) |
设灰度图阈值为τ,则图像的像素可以分为C0与C1两类(卫星与背景),C0表示灰度值大小为[0, 1, …, τ]的像素,C1表示灰度值大小为[τ+1, τ+2, …, 255]的像素。2类像素的概率分布分别为

|
(35) |
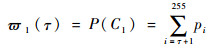
|
(36) |
均值分别为

|
(37) |
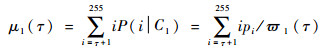
|
(38) |
令灰度图的总平均值为μT,则有
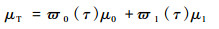
|
(39) |
式中: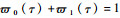
C0与C1之间的类间方差σB2可以表示为
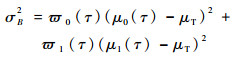
|
(40) |
则最佳阈值τ*通过最大化类间方差σB2得到,即

|
(41) |
在算法实现过程中,当σB2取最大值时,阈值τ即为最佳阈值τ*,从而将卫星从背景中分离,得到图 5。
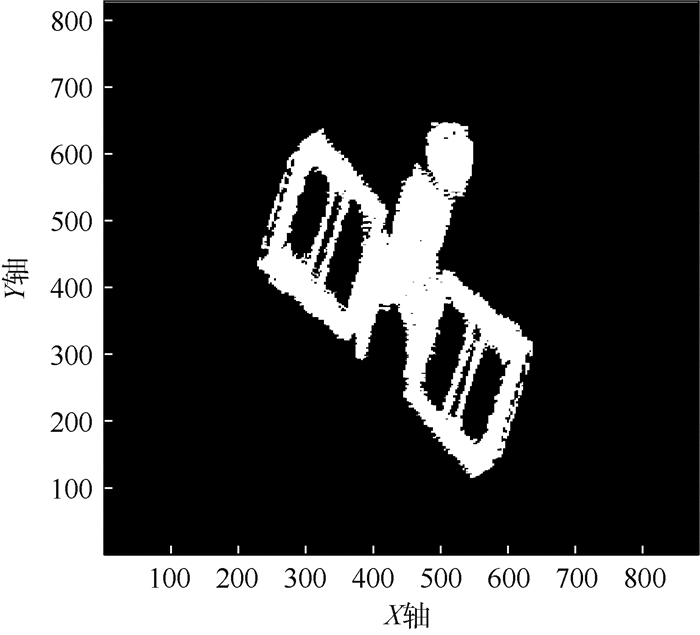
|
| 图 5 目标卫星ISAR像的二值化结果 Fig. 5 Binarization results of target satellite ISAR image |
将卫星从背景中分离后,为了对卫星进行旋转处理,首先需要对卫星的边缘进行检测。边缘检测算法种类较多,以Roberts、Sobel、Kirsch、Prewitt及高斯-拉普拉斯等为代表的边缘检测算子受噪声影响较大,难以满足实际应用要求。因此,本文采用最优边缘检测算法——canny算子。canny算子不易受噪声干扰,同时能够检测出真正的弱边缘,是目前应用最为广泛的边缘检测算子之一。
canny算子在进行卫星边缘检测时,主要分为以下3个步骤进行:
步骤1 二维高斯平滑滤波。边缘检测算法对噪声十分敏感,因此在进行canny算子边缘检测前,有必要对图像进行去噪处理。通过采用二维高斯函数的一阶导数与图像进行卷积运算,从而得到滤掉高频噪声后的图像。其中,二维高斯函数的表达式为

|
(42) |
式中:(xt, yt)为卫星ISAR图像中的每一点;σ由高斯滤波器的宽度决定,其取值大小影响图像的平滑程度。
G(xt,yt)的一阶导数为

|
(43) |
在运算过程中,为了提高运算速度,将二维滤波器
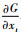
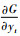
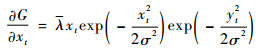
|
(44) |
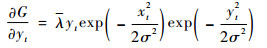
|
(45) |
式中:λ为常量。
将2个一维滤波器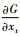
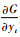

|
(46) |
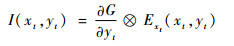
|
(47) |
式中:I(xt, yt)为平滑滤波后所得图像。
步骤2 梯度幅值与梯度方向计算,以及梯度幅值的非极大值抑制。利用2×2邻域一阶偏导的有限差分方法,计算平滑滤波后图像I(xt, yt)的梯度幅值与梯度方向。将水平方向与垂直方向的偏导分别存储在Pxt(i, j)、Pyt(i, j) 2个数组中。

|
(48) |
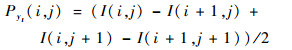
|
(49) |
利用式(48)、式(49),计算得到I(xt, yt)的梯度幅值M(i, j)与梯度方向H(i, j)分别为
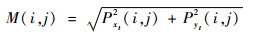
|
(50) |
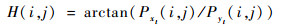
|
(51) |
在计算过程中,若图像I(xt, yt)中像素点(i, j)的梯度幅值M(i, j)大于或等于沿H(i, j)梯度方向任意相邻2点像素之间的梯度幅值,则认为该点为可能的边缘点。
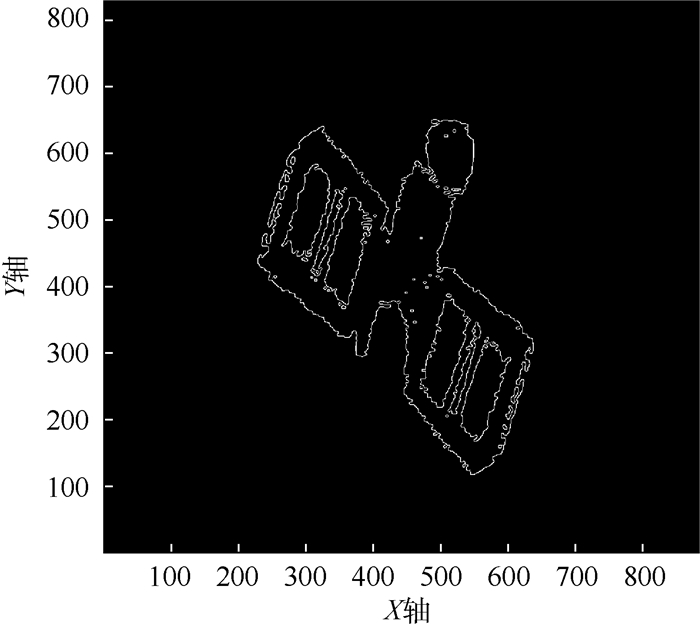
步骤3 基于双阈值法的边缘确定。步骤2中确定了所有的可能边缘,为了进一步得到图像的真实边缘,采用高低双阈值方法,将所有边缘分为T1(i, j)与T2(i, j)两类。其中,T1(i, j)由高阈值确定,不含假边缘,但有可能存在边缘的间断不连续。对此,当T1(i, j)出现边缘间断现象时,在低阈值确定的T2(i, j)中利用8邻域位置搜寻方法寻找可以连接到间断轮廓上的边缘,并通过递归跟踪算法,直至最终补全T1(i, j)中所有间断边缘,从而实现图像的边缘检测。检测结果如图 6所示。
|
| 图 6 目标卫星ISAR像的边缘检测结果 Fig. 6 Edge detection results of target satellite ISAR images |
实现卫星图像的边缘检测后,需要进一步对图像进行旋转校正。旋转校正需要确定卫星的纵轴(最长轴),对此本文采用Hough变换方法进行检测。
Hough变换对图像局部缺损不敏感,且对噪声具有较强鲁棒性。其基于“点-线”对偶原理,将原有空间坐标系中的一条直线映射为参数空间中无数条曲线同时相交的一个点,进而将直线的检测问题转化为参数空间中点的检测问题,并通过参数空间中点的统计累加实现直线检测。具体过程如下:
基于方程ρ=xtcos ζ+ytsin ζ将图像中的每一点(xt, yt)映射为参数空间中的一条正弦曲线,ρ与ζ为一对变量。遍历ζ值,计算ρ值,并根据ζ值与ρ值对二维累加器矩阵进行累加,得到共线点的个数。其中,ζ的取值范围为[0°, 180°],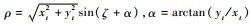
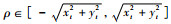

|
| 图 7 直角坐标系中线到参数空间点的映射 Fig. 7 Lines in a rectangular coordinate system mapped to points in parameter space |
利用Hough变换检测卫星纵轴(最长轴)的具体算法步骤如下:
步骤1 在ρ与ζ合适的取值范围内建立一个离散的参数空间。
步骤2 将参数空间量化为l1×l2个单元(l1为ζ的等分个数,l2为ρ的等分个数),并建立累加器矩阵。
步骤3 初始化l1×l2个累加器,分配给参数空间中的每个单元。
步骤4 将卫星图像中的点(xt, yt)代入方程ρ=xtcos ζ+ytsin ζ,根据每个量化的ζ值计算ρ值。
步骤5 将计算得到的ζ值与ρ值代入相应的离散化参数空间中,并将对应位置的计数器值加1。
步骤6 当遍历完卫星图像中所有点后,检验离散空间中每个累加器的值,当累加器值为最大时,其所对应的ζ与ρ值即为所求直线的参数,代入方程ρ=xtcos ζ+ytsin ζ中即可求得的卫星的纵轴(最长轴)。
检测结果如图 8所示。

|
| 图 8 基于Hough变换的卫星边缘直线检测过程 Fig. 8 Satellite edge line detection process based on Hough transform |
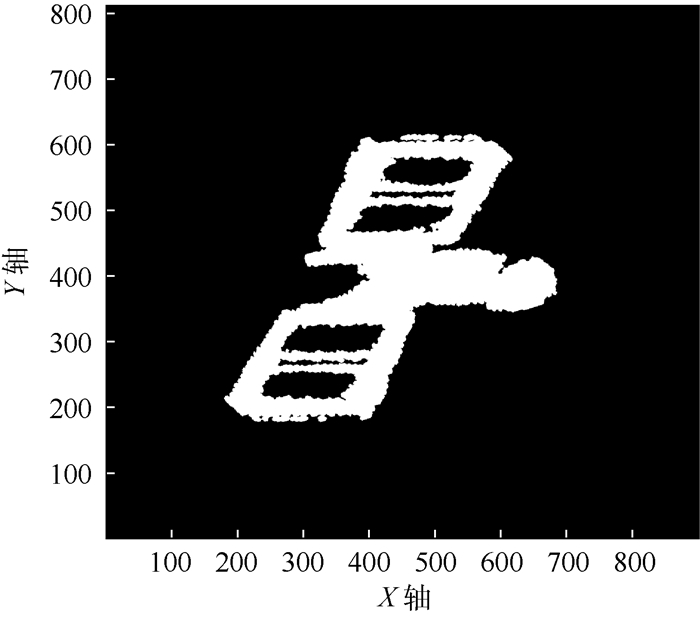
根据所求ζ值,将卫星图像顺时针旋转π/2-ζ,从而实现图像的纵轴(最长轴)与像平面的横轴平行,如图 9所示。
|
| 图 9 目标卫星ISAR像的旋转校正结果 Fig. 9 Rotation correction results of target satellite ISAR images |
从卫星的二值图像中可以看到,卫星内部存在大量的孔洞,并且由于雷达脉冲旁瓣干扰的存在,卫星周围出现许多孤立的噪声区域。因此,为了提高图像质量,填充卫星内部孔洞,平滑卫星边界,且保持卫星形状、大小不变,提出利用二值形态学中的闭运算对3.2节中得到的卫星图像进行进一步处理。
二值形态学中的闭运算被定义为利用相同的“结构元素(structure element)”先后对二值图像进行膨胀运算与腐蚀运算的一种数学形态计算算子。其中,结构元素是二值形态学中的基本算子,通过与卫星图像中每个像素的周围区域进行特定的逻辑运算,得到每个像素位置新的像素值。像素值大小由结构元素的形状、大小及逻辑运算性质决定。结构元素包括圆形、矩形、菱形、直线等多种形状,鉴于正方形结构元素具有各向同性且操作性较强的优点,采用正方形结构元素进行闭运算。
根据闭运算的操作顺序,先对卫星图像进行膨胀运算。膨胀运算可以填补卫星内部孔洞,并使卫星边界变得平滑。假设卫星图像为F,结构元素为J,令结构元素J在像平面上依次移动,当经过每一个像素点时,J[s]有以下3种状态,如图 10所示:①J[s1]⊆F;②J[s2]⊆Fc;③J[s3]∩F≠Ø, J[s3]∩Fc≠Ø。

|
| 图 10 J[s]的3种可能状态 Fig. 10 Three possible states of J[s] |
膨胀运算对应上述第3种状态,J[s]与F部分相关,将F中的每一像素点扩展为结构元素J,得到新的图像可以描述为

|
(52) |
腐蚀运算可以去除孤立噪声区域,同时恢复卫星尺寸大小。腐蚀运算对应上述第1种状态,J[s]与F最大相关,通过腐蚀运算后的图像可以描述为
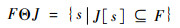
|
(53) |
综上,图像闭运算后得到的图像为
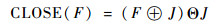
|
(54) |
闭运算算法步骤可以描述如下:
步骤1 输入旋转后的二值图像,大小为Mt×Nt。
步骤2 选择正方形结构元素,并设置结构元素大小为nJ×nJ。
步骤3 膨胀运算。for i=1 to Mt;for j=1 to Nt。将(i, j)作为当前处理像素,若当前像素值为1,直接操作下一个像素;若当前像素值为0,判断周围nJ×nJ-1个像素是否全为0,若至少存在一个像素值为1,则将该像素值设置为1,否则操作下一个像素。
步骤4 腐蚀运算。for i=1 to Mt;for j=1 to Nt。将(i, j)作为当前处理像素,若当前像素值为0,直接操作下一个像素;若当前像素值为1,判断周围nJ×nJ-1个像素是否全为1,若至少存在一个像素值为0,则将该像素值设置为0,否则操作下一个像素。
步骤5 输出图像,运算结束。
运算结果如图 11所示。

|
| 图 11 目标卫星二值图像的闭运算结果 Fig. 11 Closed operation results of target satellite binary image |
在卫星识别过程中,为了避免卫星在图像中出现位置不确定的状况,同时提高识别速度,本文利用形态学中的连通域思想,将卫星所在区域分割出来。首先标记二值图中的所有连通域,根据连通域几何特征,求得表征卫星的最大连通域,在此基础上,计算连通域的几何中心,并以该点为参考点分割出像素值大小为a×a的子区域。具体的算法步骤如下:
步骤1 输入二值图像F′(i, j)。
步骤2 采用4邻域网格进行逐像素扫描。若当前检测点(i, j)的像素值为0,则继续扫描下一个点。
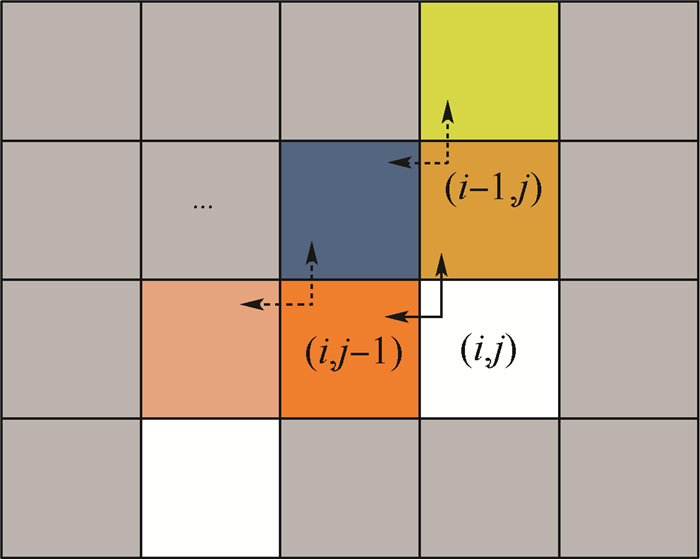
步骤3 若当前检测点的像素值为1,则继续检测其左侧点(i, j-1)及上侧点(i-1, j),如图 12所示。并根据左侧点像素值ILeft及上侧点像素值IUp的大小,将检测结果分成4种情况:①ILeft与IUp均为0,则给该像素点一个新的标记(新的连通域);②ILeft与IUp只有一个为1,则给该像素点与像素值为1的点相同的标记;③ILeft与IUp均为1,且具有相同的标记,则给该像素点与其相同的标记;④ILeft与IUp均为1,但具有不同的标记,将该像素点标记为较小的标记值。
|
| 图 12 邻域回溯法求连通域示意图 Fig. 12 Schematic diagram of neighborhood backtracking method to find connected domain |
步骤4 继续回溯,每次执行步骤3中的①~④,直到回溯到连通域的开始元素。
步骤5 继续执行步骤2,直到二值图中所有的像素点被检测完。
步骤6 计算所有连通域的面积Sconnect(连通域中的像素个数),保留最大连通域SMAX,计算SMAX的几何中心(xtc, ytc)。
步骤7 定义矩阵Fa×a″,并为其赋值,令
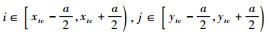
分割结果如图 13所示。

|
| 图 13 目标卫星子区域分割结果 Fig. 13 Segmentation results of target satellite subregion |
卫星轮廓是图像识别过程中最主要的特征之一,为此,继续对3.4节中生成的图像进行卫星轮廓提取。本文轮廓提取算法可以描述为
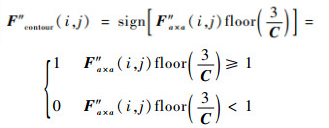
|
(55) |
式中:
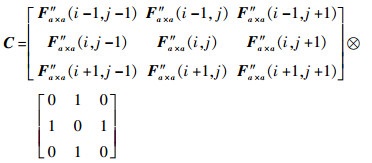
|
(56) |
其中:Fcontour″(i, j)为提取的卫星轮廓;sign为符号函数;floor为向0取整函数;C为像素点(i, j)在水平与垂直方向上4个相邻像素点的强度值加和。
卫星的轮廓提取结果如图 14所示。可以看到,卫星轮廓线能够较好地勾勒出卫星的外形结构,该特征对于进一步展开卫星的识别工作具有的重要意义。
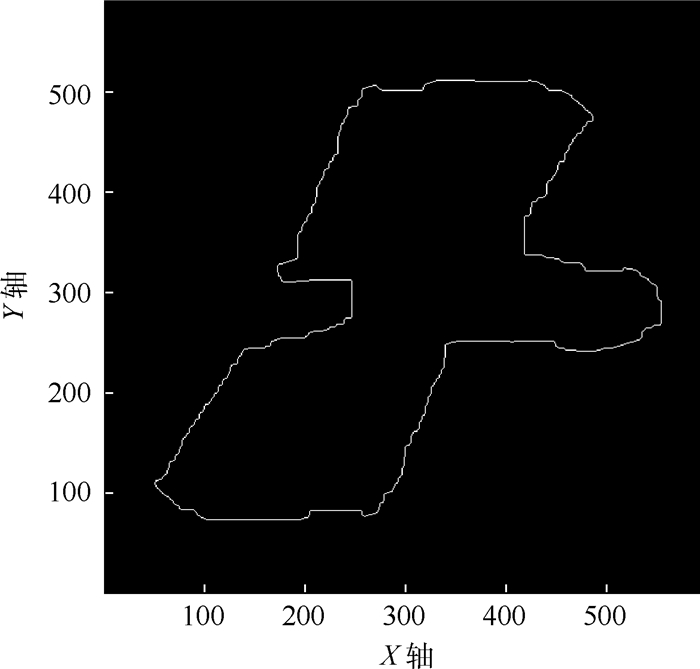
|
| 图 14 目标卫星轮廓提取结果 Fig. 14 Extraction results of target satellite contour |
本文基于在轨卫星的三维几何结构建立了空间目标的ISAR成像模型,经过坐标转换、卫星运动轨迹分解、单位合成孔径时间内的脉冲周期数求解等步骤,建立了ISAR成像模型及图像函数提取模型,经过噪声抑制等初步处理得到了卫星的ISAR像;从ISAR像的自身特征出发,设计了空间目标ISAR像处理算法及轮廓提取算法,建立了较为连续的空间目标轮廓特征提取模型,计算结果显示,提取出的目标卫星的轮廓平滑且连续,为进一步展开空间目标识别奠定重要基础。
本文设计的图像处理算法的优点主要体现在如下方面:
1) 算法结构简单,程序实现容易,对于受噪声干扰及轮廓线受损的ISAR像具有较好的处理效果。
2) 图像处理的每个步骤均具有较高的处理效率,处理后的ISAR像结构清晰,旋转校正效果良好,较好地填充了卫星内部孔洞,并去除了目标周围孤立的噪声区域。
3) 算法结构灵活,对于不同形状、帧中位置任意分布的ISAR像均可利用该算法进行处理。
| [1] |
TOUMI A, HOELTZENER B, KHENCHAF A. Hierarchical segmentation on ISAR image for target recognition[J]. International Journal of Computational Intelligence Research, 2009, 5(1): 63-71. |
| [2] |
BENEDETTO F, FULGINEI F, RLAUDANI A, et al. Automatic aircraft target recognition by ISAR image processing based on neural classifier[J]. International Journal of Advanced Computer Science and Applications, 2012, 3(8): 96-103. |
| [3] |
ASGHARI M H, JALALI B. Edge detection in digital images using dispersive phase stretch transform[J]. International Journal of Biomedical Imaging, 2015, 2015: 687819. |
| [4] |
STANKOVIC L. ISAR image analysis and recovery with unavailable or heavily corrupted data[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2093-2106. DOI:10.1109/TAES.2015.140413 |
| [5] |
LEE S J, BAE J H, KANG B S, et al.Classification of ISAR images using sparse recovery algorithms[C]//IEEE Conference on Antenna Measurements & Applications.Piscataway, NJ: IEEE Press, 2014: 1-4.
|
| [6] |
唐宁, 高勋章, 黎湘. ISAR像自动识别中的预处理算法[J]. 系统工程与电子技术, 2011, 33(9): 2002-2006. TANG N, GAO X Z, LI X. Preprocessing algorithm for ISAR image automatic recognition[J]. Systems Engineering and Electronics Technology, 2011, 33(9): 2002-2006. DOI:10.3969/j.issn.1001-506X.2011.09.16 (in Chinese) |
| [7] |
MUSMAN S, KERR D, BACHMANN C. Automatic recognition of ISAR ship images[J]. IEEE Transactions of Aerospace and Electronic Systems, 1996, 32(4): 1392-1404. DOI:10.1109/7.543860 |
| [8] |
BACHMANN C M, MUSMAN S A, SCHULTZ A.Classification of simulated radar imagery using lateral inhibition neural networks[C]//Neural Networks for Signal Processing.Piscataway, NJ: IEEE Press, 1992: 279-288.
|
| [9] |
ZELJKOVIC V, LI Q, VINCELETTE R, et al. Automatic algorithm for inverse synthetic aperture radar images recognition and classification[J]. IET Radar Sonar Navigation, 2010, 4(1): 96-109. DOI:10.1049/iet-rsn.2009.0112 |
| [10] |
JDEY I, TOUMI A, DHIBI M, et al.The contribution of fusion techniques in the recognition systems of radar targets[C]//IET International Conference on Radar Systems.London: IET, 2012: 1-5.
|
| [11] |
唐宁, 高勋章, 黎湘. 基于几何散列法的ISAR像自动目标识别[J]. 系统工程与电子技术, 2012, 34(4): 692-697. TANG N, GAO X Z, LI X. Automatic target recognition of ISAR images based on geometric hash[J]. Systems Engineering and Electronic Technology, 2012, 34(4): 692-697. DOI:10.3969/j.issn.1001-506X.2012.04.10 (in Chinese) |
| [12] |
TANG N, GAO X Z, LI X. Target classification of ISAR images based on feature space optimization of local non-negative matrix factorisation[J]. IET Signal Processing, 2012, 6(5): 494-502. DOI:10.1049/iet-spr.2011.0286 |
| [13] |
李飞.雷达图像目标特征提取方法研究[D].西安: 西安电子科技大学, 2014: 25-100. LI F.Study on target feature extraction based on radar image[D].Xi'an: Xidian University, 2014: 25-100(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D551838 |
| [14] |
王欣.基于酉ESPRIT的超分辨ISAR成像及其应用[D].西安: 西安电子科技大学, 2015: 31-74. WANG X.Unitary ESPRIT based on superresolution ISAR imaging and its application[D].Xi'an: Xidian university, 2015: 31-74(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10701-1016006285.htm |
| [15] |
王芳, 盛卫星, 马晓峰, 等. 基于直方图统计量的逆合成孔径雷达目标识别[J]. 电波科学学报, 2012, 27(4): 92-98. WANG F, SHENG W X, MA X F, et al. Target clarification for ISAR image based on histogram statistics[J]. Journal of Radio Science, 2012, 27(4): 92-98. (in Chinese) |
| [16] |
王芳, 盛卫星, 马晓峰, 等. 基于B(2D)2PGNMF的ISAR像目标识别[J]. 南京理工大学学报(自然科学版), 2013, 37(6): 863-868. WANG F, SHENG W X, MA X F, et al. ISAR image target recognition based on B(2D)2PGNMF[J]. Journal of Nanjing University of Science and Technology(Natural Science), 2013, 37(6): 863-868. DOI:10.3969/j.issn.1005-9830.2013.06.014 (in Chinese) |
| [17] |
王芳, 盛卫星, 马晓峰, 等. 基于Gabor幅值特征和相位特征相融合的ISAR像目标识别[J]. 电子与信息学报, 2013, 35(8): 1813-1819. WANG F, SHENG W X, MA X F, et al. ISAR image recognition with fusion of Gabor magnitude and phase feature[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1813-1819. (in Chinese) |



