Download PDF  
文章快速检索  
  高级检索
引用格式
靳涛, 胡小平, 于保华. 大端接圆柱杆的复合圆锥形变幅杆设计及应用[J]. 北京航空航天大学学报, 2019, 45(8): 1630-1638.
JIN T, HU X P, YU B H. Design and application of compound conical horn with cylinder at big end[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2019, 45(8): 1630-1638.
大端接圆柱杆的复合圆锥形变幅杆设计及应用
靳涛, 胡小平, 于保华     
杭州电子科技大学 机械工程学院, 杭州 310018
收稿日期: 2018-11-28; 录用日期: 2019-02-02; 网络出版时间: 2019-03-01 13:25
基金项目: 国家自然科学基金(51475130);浙江省自然科学基金(LY17E050025)
作者简介: 靳涛  男, 硕士研究生。主要研究方向:特种精密加工技术、声学系统组件;
胡小平  女, 博士, 教授。主要研究方向:特种精密加工技术、设计理论与方法、知识工程;
于保华  男, 博士, 高级工程师。主要研究方向:特种精密加工、精密测量及控制
通信作者: 胡小平, E-mail: xiaoping.hu@hdu.edu.cn
摘要: 针对目前国产超声变幅杆耐用性较差的问题，设计一种新型复合变幅杆，满足振幅的条件下，使变幅杆具有较小的工作应力。通过波动方程建立新型复合变幅杆参数方程，着重计算了放大倍数、形状因数及应力极大点等参数。首先，采用有限元分析软件对变幅杆进行动力学分析，得到的结果与理论结果进行比较，验证了理论公式的正确性。然后，在此基础上与圆锥形变幅杆、指数形变幅杆及小端接圆柱杆的复合圆锥形变幅杆进行比较，结果表明新型复合变幅杆具有更好的综合性能和更小的最大应力。最后，基于ANSYS Workbench优化设计功能对变幅杆进行优化修整，对优化后的变幅杆进行阻抗分析和振动性能测试，测试结果表明新型复合变幅杆理论性能参数与实验测试结果基本一致，变幅杆的谐振频率为20 013 Hz，当换能器输出振幅峰峰值为13 μm时，变幅杆的输出端振幅峰峰值可达40 μm，变幅杆振幅实际放大倍数为3.08，满足切削实验振幅的要求。
关键词: 综合性能     寿命     最大应力     优化设计     有限元分析    
Design and application of compound conical horn with cylinder at big end
JIN Tao, HU Xiaoping, YU Baohua     
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, China
Received: 2018-11-28; Accepted: 2019-02-02; Published online: 2019-03-01 13:25
Foundation item: National Natural Science Foundation of China (51475130); Natural Science Foundation of Zhejiang Province (LY17E050025)
Corresponding author. HU Xiaoping, E-mail: xiaoping.hu@hdu.edu.cn
Abstract: Aimed at the problem of poor durability of the domestic ultrasonic horn, a new type of compound horn is designed to meet the amplitude and make the horn have a small working stress.The new composite horn parameter equation is established by the wave equation, and the parameters such as magnification, shape factor and stress maximum point are calculated.Frist, the finite element analysis software was used to analyze the kinetics of the horn. The obtained results were compared with the theoretical results to verify the correctness of the theoretical formula. Second, on the basis of this, compared with the conical horn, the exponential deformation horn and compound conical horn with cylinder at big end, the results show that the new composite horn has better comprehensive performance and smaller maximum stress. Finally, based on ANSYS Workbench optimization design function, the horn is optimized and trimmed, and the optimized horn is subjected to impedance analysis and vibration performance test. The test results show that the theoretical performance parameters of the new composite horn are basically consistent with the experimental test results. The resonant frequency of the rod is 20 013 Hz. When the transducer peak-to-peak value of the output amplitude is 13 μm, the peak-to-peak value of the output amplitude of the horn can reach 40 μm, and the amplitude amplification factor of the horn is 3.08, which satisfies the requirements of the cutting experiment amplitude.
Keywords: comprehensive performance     life     maximum stress     optimization design     finite element analysis    

超声切削加工系统一般包括超声波发生器、换能器、变幅杆和加工刀具等[1-2]。由于换能器输出振幅不能满足刀具加工需要，需在换能器与加工刀具之间添加一种振幅放大机构，即变幅杆[3]。

超声变幅杆是超声切削加工系统中的重要组成部件，其作用是把换能器输出端的振动位移或速度振幅进行放大，此外，超声变幅杆还可以作为机械阻抗变换器，在换能器和声负载之间进行阻抗匹配，使超声能量更有效地从换能器向负载传输[4-6]。根据需求的不同，变幅杆可分为单一型和复合型[7]。

变幅杆的振动特性理论分析，通常基于其波动方程，由边值问题定解[8-9]。变幅杆的设计通常按照半波、空载考虑，实际应用时再加以调整[10]。在高强度超声应用中，往往要求变幅杆末端具有较大的振动幅度，这就要求变幅杆的形状因数φ和放大倍数Mp的值都尽可能大[11]。同时为了保证变幅杆能够持续工作较长时间，变幅杆工作时应具有较小的最大应力。为了兼顾以上优点，设计了一种新型复合变幅杆。

本文首先基于传统的振动理论，设计一种1/2波长大端接圆柱杆的复合圆锥形变幅杆(简称为新型复合变幅杆)；然后借助有限元分析软件验证其理论公式的正确性，并且与单一型变幅杆以及小端接圆柱杆的复合圆锥形变幅杆的性能参数进行比较，利用有限元分析软件对新型复合变幅杆进行优化设计，并通过实验验证了其振动情况。

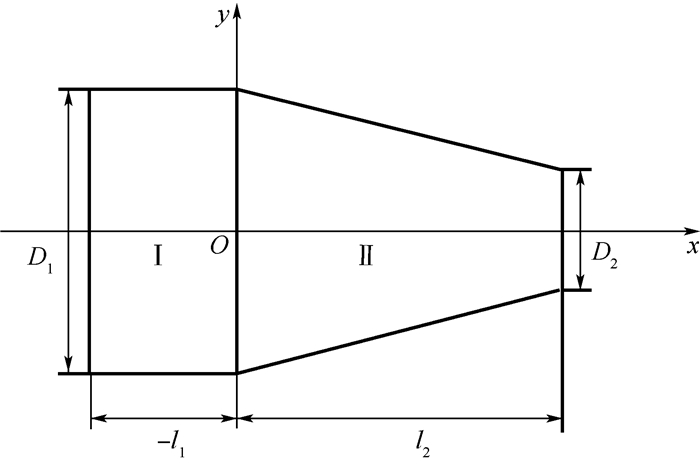
1 新型复合变幅杆的理论模型

图 1为新型复合变幅杆的示意图，为了简化模型，假设变幅杆由均匀、各向同性材料构成。

图 1 新型复合变幅杆 Fig. 1 New compound horn
图选项

在简谐共振的条件下，变幅杆纵向振动的波动方程为[12]

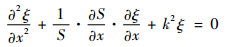
(1)

式中:S=S(x)为变幅杆的横截面积函数；ξ=ξ(x)为质点位移函数；k=ω/c，k为圆波数，ω为圆频率，c为纵波在变幅杆中的传播速度。

设Ⅰ段的末端为坐标原点，则各段的面积函数表达式为

(2)

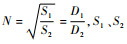
式中:l1、l2分别为两段变幅杆的长度；锥度系数分别为首尾两端变幅杆的直径，面积系数分别为首尾两端变幅杆的横截面积。

将每段变幅杆的面积函数代入波动方程式(1)中，并联立式(3)~式(5):

自由边界条件为

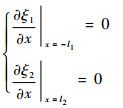
(3)

变幅杆左端位移边界条件为

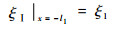
(4)

两段变幅杆之间的位移、应变连续条件为

(5)

解得每段变幅杆的位移函数为

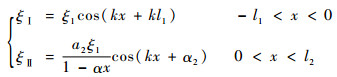
(6)

应变分布的表达式为

(7)

式中：。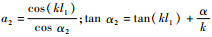

1) 频率方程

由式(7)和边界条件(3)可以推导出变幅杆的频率方程为

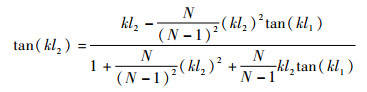
(8)

由式(8)求出根(kl2)之后，可由式(9)求出l2长度：

(9)

式中：λ为波长。

2) 位移节点x0

由式(6)，当x=x0时ξ=0得节点位移x0为

(10)

3) 放大倍数Mp

由式(6)及边界条件ξⅡ|x=l2=ξ2可得

(11)

4) 输入力阻抗Zi

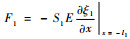
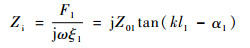
由式(7)及边界条件可得

(12)

式中：F1为输入端的力; E为弹性模量; tan α1=tan 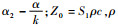为变幅杆的材料密度。

5) 形状因数φ

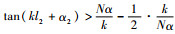
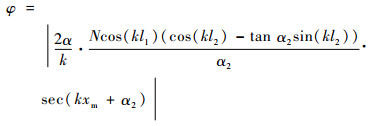
当满足条件时，φ和包含应变极大点xm的超越方程为

(13)
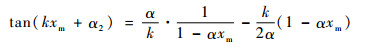
(14)

当不满足条件时，则Ⅱ段没有应变极大点，应变最大点在xm=l2处，则φ=1。

2 变幅杆的动力学分析

利用ANSYS Workbench有限元分析软件对所设计的新型复合变幅杆进行动力学分析，通过比较各项参数，验证理论公式的正确性。

2.1 理论数据计算

在变幅杆设计中，需要进行大量的数学计算，其中包括求解超越方程。这些计算很难用手工精确和快速的进行，这就需要借助MATLAB软件计算。

由频率方程可知，变幅杆的各项参数不仅和面积系数N有关还与Ⅰ段l1有关。

分别假设Ⅰ段长度l1=31.25 mm以及面积系数N=3.5，变幅杆工作时的谐振频率FREQ=20 000 Hz，通过式(8)求得不同的面积系数N时圆锥杆的长度l2以及不同的Ⅰ段长度l1时圆锥杆的长度l2，然后由式(11)、式(13)和式(14)分别求得相应的放大倍数Mp、形状因数φ和应变极大点xm，结果如表 1、表 2所示。

表 1 N对变幅杆性能参数的影响 Table 1 Effect of N on performance parameters of horn
样本编号 N l2/mm Mp φ xm/mm
1 1.077 94.31 1.09 1.05 33.13
2 1.167 95.50 1.20 1.10 35.12
3 1.272 96.70 1.32 1.16 37.27
4 1.4 97.89 1.47 1.22 39.63
5 1.556 99.88 1.63 1.29 42.21
6 1.75 101.87 1.83 1.37 45.07
7 2 104.66 2.06 1.45 48.24
8 2.333 108.24 2.32 1.54 51.64
9 2.8 112.22 2.65 1.65 55.49
10 3.5 117.39 3.02 1.78 59.37
注：l1=31.25 mm，FREQ=20 000 Hz。
表选项

表 2 l1对变幅杆性能参数的影响 Table 2 Effect of l1 on performance parameters of horn
样本编号 l1/mm l2/mm Mp φ xm/mm
1 1.99 139.67 2.94 1.705 82.46
2 3.97 138.08 2.95 1.695 80.95
3 5.92 136.49 2.97 1.716 78.86
4 7.85 134.88 2.98 1.711 77.44
5 15.14 128.92 3.04 1.746 71.37
6 21.50 124.14 3.06 1.741 67.02
7 26.85 120.56 3.03 1.767 62.51
8 31.25 117.39 3.02 1.780 59.37
9 34.86 115.00 2.98 1.792 56.58
10 37.82 113.01 2.94 1.794 54.49
11 40.27 111.02 2.93 1.806 52.97
12 42.32 109.83 2.88 1.801 51.42
13 44.05 108.64 2.85 1.801 50.23
14 47.36 106.25 2.79 1.822 47.55
15 49.70 104.66 2.74 1.825 45.74
16 51.43 103.46 2.70 1.826 44.40
17 52.75 102.27 2.68 1.834 43.60
18 55.93 99.88 2.60 1.843 41.09
19 57.55 98.69 2.56 1.859 39.37
20 58.53 97.89 2.53 1.867 38.47
注：N=3.5，FREQ=20 000 Hz。
表选项

2.2 动力学分析结果与理论数据比较

由于变幅杆工作过程中一直处在高频的振动状态，因此所选材料必须具有一定的强度和韧性[13]。试验选用性能优良的00Cr17Ni14Mo2材料来制作变幅杆，材料参数如表 3所示。

表 3 00Cr17Ni14Mo2材料参数 Table 3 00Cr17Ni14Mo2 material parameters
参数 数值
密度ρ/(kg·m－3) 8 000
弹性模量E/Pa 2.06×1011
泊松比μ 0.28
表选项

利用CAD软件对变幅杆建模，导入ANSYS Workbench软件中，对变幅杆进行模态分析，提取各阶模态，选取纵振情况下的谐振频率。在模态分析的基础上，选用Harmonic Response模块对变幅杆进行谐响应分析，法兰的位移为零，在变幅杆大端xy平面施加0.04 mm的位移载荷，得到变幅杆的放大倍数Mp、应变极大点xm和最大应力σmax。

对表 1、表 2不同结构参数的变幅杆进行动力学分析，结果如表 4、表 5所示。

表 4 N对动力学分析的影响 Table 4 Effect of N on kinetic analysis
样本编号 N FREQ/Hz Mp σmax/MPa xm/mm
1 1.077 20 431 1.14 23.99 34.46
2 1.167 20 355 1.25 25.416 36.45
3 1.272 20 318 1.36 26.926 38.56
4 1.4 20 330 1.50 26.341 41.05
5 1.556 20 273 1.66 27.002 43.51
6 1.75 20 275 1.86 28.745 45.97
7 2 20 239 2.08 30.578 48.80
8 2.333 20 180 2.35 32.287 51.98
9 2.8 20 250 2.66 34.035 55.71
10 3.5 20 330 3.02 34.65 59.49
注：l1=31.25 mm。
表选项

表 5 l1对动力学分析的影响 Table 5 Effect of l1 on kinetic analysis
样本编号 l1/mm FREQ/Hz Mp σmax/MPa xm/mm
1 1.99 20 518 3.00 35.85 81.25
2 3.97 20 489 3.02 35.85 79.84
3 5.92 20 474 3.02 35.81 77.79
4 7.85 20 455 3.04 36.01 76.46
5 15.14 20 449 3.07 35.93 70.57
6 21.50 20 414 3.07 35.76 66.35
7 26.85 20 352 3.05 35.17 61.91
8 31.25 20 330 3.02 34.65 59.05
9 34.86 20 296 2.98 33.94 55.78
10 37.82 20 282 2.94 33.32 53.68
11 40.27 20 311 2.90 32.74 51.98
12 42.32 20 275 2.87 32.35 50.42
13 44.05 20 260 2.83 31.87 49.23
14 47.36 20 263 2.76 30.88 46.58
15 49.70 20 254 2.70 30.35 44.54
16 51.43 20 251 2.66 29.65 43.18
17 52.75 20 276 2.63 29.25 42.14
18 55.93 20 295 2.54 28.91 39.59
19 57.55 20 316 2.50 28.58 37.87
20 58.53 20 359 2.47 28.15 36.82
注：N=3.5。
表选项

比较表 1和表 4求解的结果，Ⅰ段长度l1保持不变时，谐振频率FREQ、放大倍数Mp和应变极大点xm的相对误差如表 6所示。

表 6 N对相对误差的影响 Table 6 Effect of N on relative error
样本编号 N FREQ相对误差Δ1/% Mp相对误差Δ2/% xm相对误差Δ3/%
1 1.077 2.16 4.59 4.01
2 1.167 1.78 4.17 3.79
3 1.272 1.59 3.03 3.46
4 1.4 1.65 2.04 3.58
5 1.556 1.37 1.84 3.08
6 1.75 1.38 1.64 2.00
7 2 1.20 0.97 1.16
8 2.333 0.90 1.29 0.66
9 2.8 1.25 0.38 0.40
10 3.5 1.65 0 0.20
注：l1=31.25 mm。
表选项

比较表 2和表 5的求解的结果，面积系数N保持不变时，谐振频率FREQ、放大倍数Mp和应变极大点xm的相对误差如表 7所示。

表 7 l1对相对误差的影响 Table 7 Effect of l1 on relative error
样本编号 l1/mm FREQ相对误差Δ1/% Mp相对误差Δ2/% xm相对误差Δ3/%
1 1.99 2.59 2.19 1.47
2 3.97 2.44 2.20 1.37
3 5.92 2.37 1.83 1.36
4 7.85 2.28 1.97 1.27
5 15.14 2.25 0.90 1.12
6 21.50 2.07 0.39 1.00
7 26.85 1.76 0.63 0.96
8 31.25 1.65 0.01 0.54
9 34.86 1.48 0.03 1.41
10 37.82 1.41 0.01 1.49
11 40.27 1.56 0.89 1.87
12 42.32 1.38 0.46 1.94
13 44.05 1.30 0.55 1.99
14 47.36 1.32 1.06 2.04
15 49.70 1.27 1.34 2.62
16 51.43 1.25 1.41 2.75
17 52.75 1.38 1.88 3.35
18 55.93 1.47 2.28 3.65
19 57.55 1.58 2.51 3.81
20 58.53 1.79 2.28 4.29
注：N=3.5。
表选项

由表 6、表 7分析可知，解析法计算的结果与有限元分析的结果基本吻合，谐振频率FREQ的相对误差最大为2.59% < 5%，放大倍数Mp的相对误差最大为4.59% < 5%，应变极大点xm的相对误差最大为4.29% < 5%。因此，在可允许的范围内，验证了理论公式的正确性。

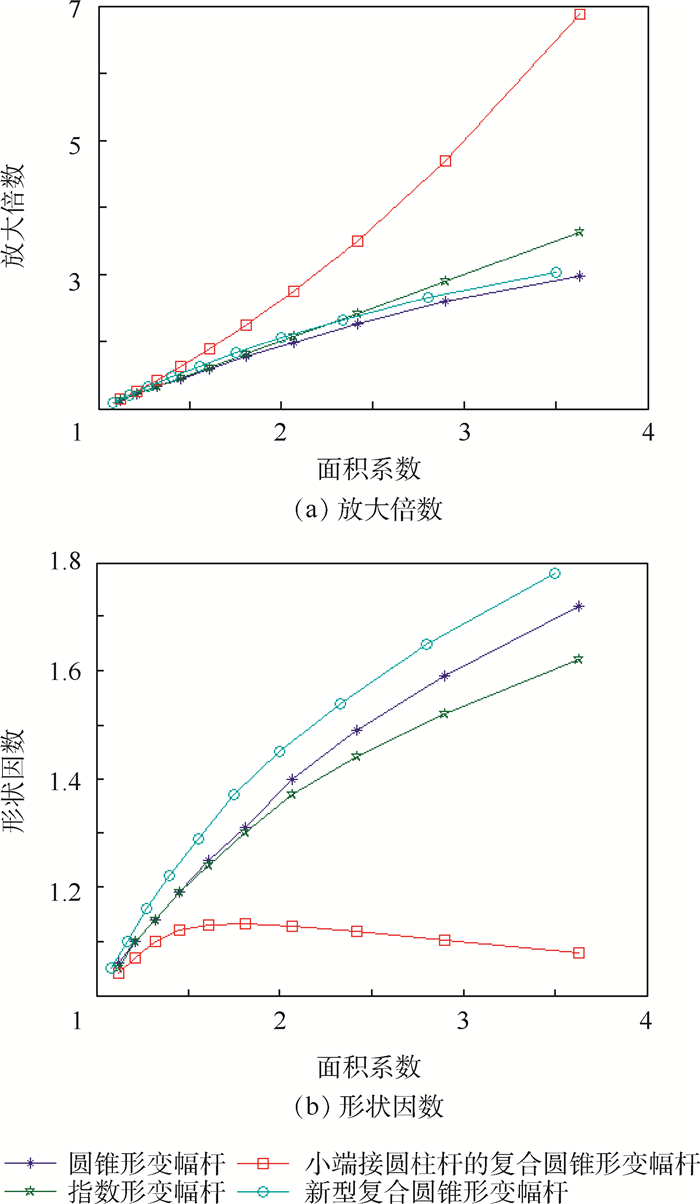
3 变幅杆性能参数和最大应力对比 3.1 变幅杆的性能参数对比

以放大倍数Mp和形状因数φ作为关键参数，与单一型变幅杆以及小端接圆柱杆的复合圆锥形变幅杆进行比较，结果如图 2所示。

图 2 各类变幅杆性能参数对比 Fig. 2 Comparison of performance parameters of various horns
图选项

由图 2可知，随着面积系数的增大，小端接圆柱杆的复合圆锥形变幅杆的放大倍数增大且增大速率最快，但是形状因数明显小于其他3种型号的变幅杆且处于较低的水平。而新型复合变幅杆的放大倍数也随着面积系数的增大而增大，一直大于圆锥形变幅杆放大倍数，与指数形变幅杆接近，并且形状因数一直大于其他3种类型的变幅杆。新型复合圆锥形变幅杆两者兼顾，变幅杆末端能达到较大的振幅，因此设计的新型复合变幅杆综合性能最优。

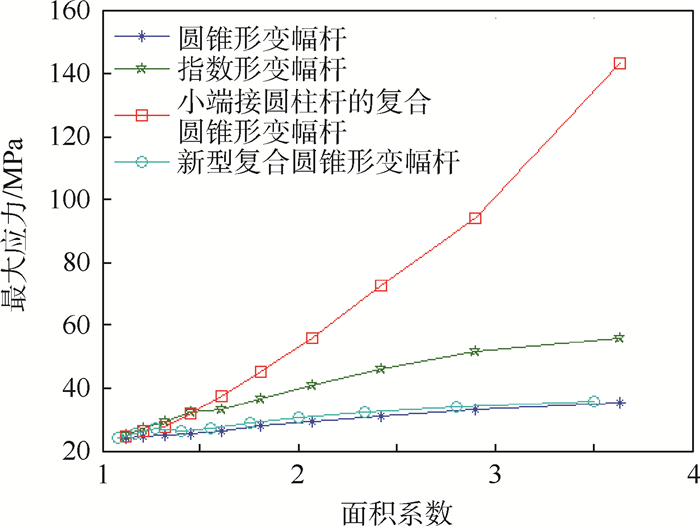
3.2 变幅杆的最大应力对比

根据材料的疲劳-寿命曲线可知，材料的性能参数相同时，变幅杆工作时的最大应力直接影响到变幅杆的寿命，为了保证变幅杆能够持续工作较长时间，具有较长的使用寿命，所以在设计变幅杆时除了要满足振幅的设计要求以外，还要重点考虑变幅杆的最大应力[14]。4种变幅杆的最大应力对比如图 3所示。

图 3 各类变幅杆最大应力对比 Fig. 3 Comparison of maximum stress of various horns
图选项

由图 3可以看出，随着面积系数的增大，各类变幅杆的最大应力都会增大。但明显可以看出，小端接圆柱杆的复合圆锥形变幅杆的最大应力随面积系数增大将快速增大，在面积系数大于1.5后明显大于其他3种变幅杆的最大应力，新型复合圆锥形变幅杆和圆锥形变幅杆的最大应力增加速度最为缓慢且一直处于较低的水平，符合设计的需求。

综合比较分析可知，新型复合变幅杆具有更好的综合性能和更小的最大应力，所以新型复合变幅杆的结构更优良。

4 新型复合变幅杆的实际应用 4.1 变幅杆的尺寸设计

为了降低换能器、刀具以及变幅杆大小端结合处的能量损耗，要求变幅杆大端直径D1等于换能器输出端直径、小端直径D2等于刀座直径[15]。在实际设计中，对于20 kHz的超声振动切削系统，根据选定的换能器型号，变幅杆的面积系数要求为N=3.5，变幅杆大端直径D1=56 mm，小端直径D2=16 mm。同时为了保证刀具的输出振幅满足要求，变幅杆的放大倍数Mp≥3。

根据表 2可知，当面积系数N=3.5时Ⅰ段长度满足条件15.14 mm < l1 < 31.25 mm，变幅杆的放大倍数可以达到Mp≥3，满足振幅的需要。当圆柱杆长度l1=31.25 mm时，最大应力较小且形状因数φ较好。所以，新型复合变幅杆的尺寸初步设计参数如表 8所示。

表 8 新型复合变幅杆参数 Table 8 New composite horn parameters
参数 数值
l1/mm 31.25
l2/mm 117.39
xm/mm 59.37
Mp 3.02
φ 1.780
表选项

由于变幅杆的大端面与换能器螺纹连接，变幅杆的小端面与刀具螺纹连接，所以需要在变幅杆的大端面和小端面各加工一个螺纹孔。

根据变幅杆设计的等效质量块法可知，为了抵消螺纹孔的影响，可以在变幅杆的小端面处沿轴向正方向增加一段短圆柱l3。

固定大端直径D1、小端直径D2，以最大应力为优化目标函数，定义设计变量l1、l2、l3，定义频率范围为19 000 Hz≤FREQ≤21 000 Hz，在保证放大倍数Mp≥3的条件下，进行变幅杆优化设计分析，优化后的变幅杆的有限元分析结果如图 4所示，得到优化后的尺寸如表 9所示。

图 4 优化后的变幅杆的有限元分析结果 Fig. 4 Finite element analysis results of optimized horn
图选项
表 9 变幅杆优化设计结果 Table 9 Results of horn design optimization
参数 优化前 优化后
l1/mm 31.25 32
l2/mm 117.39 120.51
l3/mm 4.61 4.39
FREQ/Hz 30 352 20 111
Mp 3.05 3.12
σmax/MPa 35.170 34.527
表选项

4.2 变幅杆的性能测试

根据优化设计结果，加工制作变幅杆，如图 5所示。

图 5 变幅杆实物 Fig. 5 Photo of horn
图选项

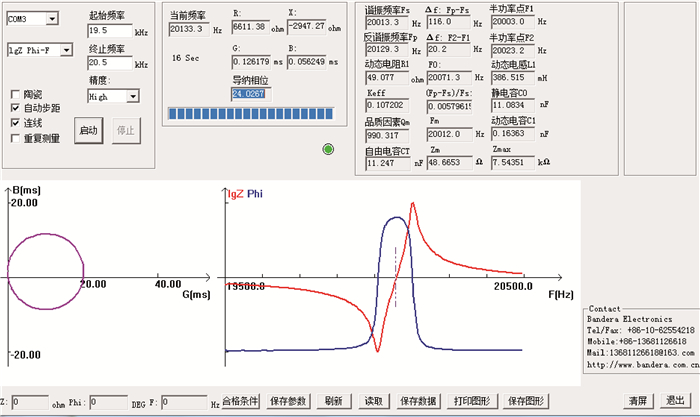
采用北京邦联时代电子科技有线公司PV70A的阻抗分析仪对换能器和变幅杆进行阻抗分析，如图 6所示。由图 6可知，变幅杆的导纳圆圆度较好，电导曲线正常。振动系统的机械品质因数较高，即系统的电声转化效率高，说明所设计变幅杆的尺寸及其结构都十分合理。变幅杆的实测频率20 013 Hz与理论设计频率20 000 Hz的误差在1%以内，进一步验证理论公式的正确性。

图 6 阻抗分析结果 Fig. 6 Result of impedance analysis
图选项

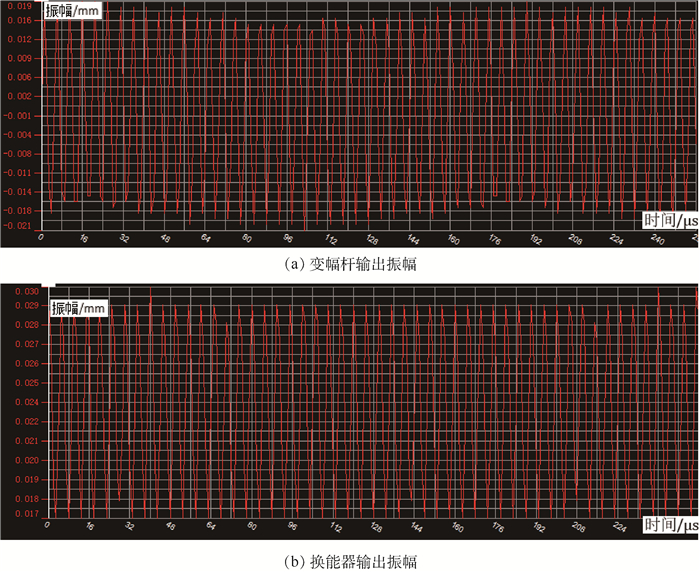
选用型号HK-008W的激光位移传感器对换能器和变幅杆的输出端进行振幅测试，在150 V驱动电压的激励下，测量换能器与变幅杆组件的输出振幅，卸载变幅杆后同样在150 V驱动电压的激励下，测量换能器的输出振幅，振幅测试的结果如图 7所示。由图 7可知：超声变幅杆系统振动状态稳定，实测变幅杆稳定输出振幅峰峰值为40 μm，换能器的输出振幅峰峰值为13 μm，变幅杆的放大倍数Mp=3.08，与理论计算结果基本吻合，证明了理论公式的正确性。

图 7 振幅测试结果 Fig. 7 Results of amplitude test
图选项

新型复合变幅杆的理论设计参数、有限元分析结果以及实测结果存在一定的误差。这主要由3方面因数造成：①理论计算时未考虑变幅杆首尾端连接螺纹孔以及窄端接修整杆l3的存在；②实验测量的是整个声学系统的谐振频率，但是理论设计和有限元分析时未考虑换能器的影响；③未能同时测量换能器与变幅杆的输出振幅，变幅杆作为纯阻负载对实验结果造成一定影响，所以实际测得的振幅放大倍数存在误差。

5 结论

各种传统形状变幅杆各具有其优点，但是都不是最理想的：圆锥形和指数形的变幅杆的振幅放大倍数较低，小端接圆柱杆的复合圆锥形变幅杆虽然具有较大的振幅放大倍数，但它的形状因数较小以及工作时具有很大的最大应力。因此采用了解析法设计了一种既能满足振幅条件，工作时最大应力较小的新型复合变幅杆。借助有限元分析软件对其进行模态和谐响应分析，得到变幅杆的谐振频率、放大倍数及应力极大点位置，与理论值基本吻合。加工和测试优化设计后的新型复合变幅杆，实测结果与理论设计参数十分接近，进一步验证了理论公式的正确性。

参考文献
[1]
冯冬菊, 赵福令, 徐占国, 等. 超声波加工工具对复合变幅杆谐振性能影响[J]. 大连理工大学学报, 2004, 44(5): 685-688.
FENG D J, ZHAO F L, XU Z G, et al. Effect of ultrasonic processing tools on resonance performance of composite horn[J]. Journal of Dalian University of Technology, 2004, 44(5): 685-688. DOI:10.3321/j.issn:1000-8608.2004.05.013 (in Chinese)
[2]
张雄, 焦锋. 超声加工技术的应用及其发展趋势[J]. 工具技术, 2012, 46(1): 3-8.
ZHANG X, JIAO F. Application of ultrasonic processing technology and its development trend[J]. Tool Engineering, 2012, 46(1): 3-8. DOI:10.3969/j.issn.1000-7008.2012.01.001 (in Chinese)
[3]
赵波, 许永强, 郑友益, 等. 基于ANSYS的超声变幅杆节点优化及振动性能试验[J]. 河南理工大学学报(自然科学版), 2014, 33(3): 304-308.
ZHAO B, XU Y Q, ZHENG Y Y, et al. Ultrasonic horn node optimization and vibration performance test based on ANSYS[J]. Journal of Henan Polytechnic University (Natural Science Edition), 2014, 33(3): 304-308. DOI:10.3969/j.issn.1673-9787.2014.03.011 (in Chinese)
[4]
胡小平, 黄仕彪, 张云电. 圆锥形变幅杆的设计及有限元分析[J]. 机电工程, 2005, 22(2): 32-36.
HU X P, HUANG S B, ZHANG Y D. Design and finite element analysis of conical horns[J]. Journal of Mechanical and Electrical Engineering, 2005, 22(2): 32-36. DOI:10.3969/j.issn.1001-4551.2005.02.009 (in Chinese)
[5]
皮钧, 纪跃波. 纵波回形变幅杆的研究[J]. 振动、测试与诊断, 2010, 30(1): 65-69.
PI J, JI Y B. Research on longitudinal wave varactors[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1): 65-69. DOI:10.3969/j.issn.1004-6801.2010.01.015 (in Chinese)
[6]
谢欣平, 田阿利, 王自力, 等. 考虑负载影响的阶梯形超声变幅杆动力特性[J]. 振动与冲击, 2012, 31(4): 157-161.
XIE X P, TIAN A L, WANG Z L, et al. Dynamic characteristics of stepped ultrasonic horns considering load effects[J]. Journal of Vibration and Shock, 2012, 31(4): 157-161. DOI:10.3969/j.issn.1000-3835.2012.04.030 (in Chinese)
[7]
张明, 衣春杰, 赵方晓, 等. 倒锥形复合变幅杆的动力学分析[J]. 电加工与模具, 2015(5): 54-57.
ZHANG M, YI C J, ZHAO F X, et al. Dynamic analysis of inverted conical composite amplitude[J]. Electrical Processing and Mold, 2015(5): 54-57. DOI:10.3969/j.issn.1009-279X.2015.05.014 (in Chinese)
[8]
SANKIN Y. Longitudinal vibrations of elastic rods of stepwise-variable cross-section colliding with a rigid obstacle[J]. Journal of Applied Mathematics & Mechanics, 2001, 65(3): 427-433.
[9]
AKKAS N. Elastic wave propagation in an exponential rod[J]. International Journal of Mechanical Sciences, 1980, 22(4): 199-208. DOI:10.1016/0020-7403(80)90035-1
[10]
EISNER E. Design of sonic amplitude transformers for high magnification[J]. Proceedings of the IEEE, 2005, 51(3): 512.
[11]
曹凤国. 超声加工技术[M]. 北京: 化学工业出版社, 2005.
CAO F G. Ultrasonic processing technology[M]. Beijing: Chemical Industry Press, 2005. (in Chinese)
[12]
林仲茂. 超声变幅杆的原理和设计[M]. 北京: 科学出版社, 1987.
LIN Z M. Principle and design of ultrasonic horn[M]. Beijing: Science Press, 1987. (in Chinese)
[13]
陈汇资, 赵波, 卞平艳, 等. 圆锥型复合变幅杆优化及动力学特性[J]. 应用声学, 2016, 35(1): 20-26.
CHEN H Z, ZHAO B, BIAN P Y, et al. Optimization and dynamic characteristics of conical composite horn[J]. Applied Acoustics, 2016, 35(1): 20-26. (in Chinese)
[14]
原丰霞, 张慧君, 朱国良. 基于ANSYS的超声变幅杆的优化设计[J]. 机械工程师, 2004(11): 24-26.
YUAN F X, ZHANG H J, ZHU G L. Optimization design of ultrasonic horns based on ANSYS[J]. Mechanical Engineers, 2004(11): 24-26. DOI:10.3969/j.issn.1002-2333.2004.11.010 (in Chinese)
[15]
潘巧生, 刘永斌, 贺良国, 等. 一种大振幅超声变幅杆设计[J]. 振动与冲击, 2014, 33(9): 1-5.
PAN Q S, LIU Y B, HE L G, et al. Large amplitude ultrasonic horn design[J]. Journal of Vibration and Shock, 2014, 33(9): 1-5. (in Chinese)
http://dx.doi.org/10.13700/j.bh.1001-5965.2018.0699
北京航空航天大学主办。
0

文章信息

靳涛, 胡小平, 于保华
JIN Tao, HU Xiaoping, YU Baohua
大端接圆柱杆的复合圆锥形变幅杆设计及应用
Design and application of compound conical horn with cylinder at big end
北京航空航天大学学报, 2019, 45(8): 1630-1638
Journal of Beijing University of Aeronautics and Astronsutics, 2019, 45(8): 1630-1638
http://dx.doi.org/10.13700/j.bh.1001-5965.2018.0699

文章历史

收稿日期: 2018-11-28
录用日期: 2019-02-02
网络出版时间: 2019-03-01 13:25

相关文章

工作空间