2. 中国运载火箭技术研究院, 北京 100076;
3. 北京航空航天大学 能源与动力工程学院, 北京 100083
2. China Academy of Launch Vehicle Technology, Beijing 100076, China;
3. School of Energy and Power Engineering, Beihang University, Beijing 100083, China
模态分析技术已广泛应用于分析线性工程结构,伴随其发展的模态综合技术在对大型复杂结构系统的动力特性分析中占有越来越重要的地位。相对而言,有关具有非线性动力学行为的大型复杂工程结构分析的进展较为缓慢。鉴于模态分析方法在线性系统分析中所显示的巨大作用,近年来研究人员也试图将非线性模态的概念引入结构分析,以期发展一套适用于非线性动力学系统的高效分析方法。例如,Jiang等[1]将非线性模态用于分析简谐激励下的系统振动特性;Touzé和Amabili[2]将非线性模态用于分析包含杜芬非线性项的减缩模型;Renson等[3]介绍了非线性模态应用于分析工程结构动力学响应;Huang等[4]将非线性模态与模态综合法结合用于分析一般非线性系统的动力学响应;Liu等[5]利用非线性模态研究了包含压电阻尼的非线性结构。为了求解各种非线性模态,衍生了多种数值计算方法,如正规形法、不变流形法、摄动法中的多尺度法,这些方法各具特点,各有其适合的范围,但真正适用于求解大型工程结构的方法并不多。
20世纪60年代初,Rosenberg[6]在其非线性模态奠基之作中指出,系统在共振区的响应可用该阶非线性模态来近似;随后,为了解决非线性模态不具叠加性问题,Szemplinska-Stupnicka[7]提出了单模态共振理论,建立了自由振动状态下的系统非线性模态和响应幅值间的关系;Jézéquel[8]和Setio[9]等分别从理论和实验的角度对该理论进行了完善和发展,将线性模态分析方法推广到求解非线性系统响应。该理论已被众多学者认可和应用[10-11],如郑兆昌[12]指出表征线性系统特性的主模态是沟通线性振动和非线性振动之间的桥梁。因此,主共振模态的计算与分析是大型复杂非线性结构动力学特性分析中至关重要的一步。
本文基于非线性模态理论及非线性动力学系统计算方法的研究进展,提炼出了一种通用的、便于数值计算的非线性模态分析方法,并给出了分析步骤。本文方法的核心是建立主共振模态的特征频率、振型与对应的模态振动幅值之间的关系,用模态参数的变化规律来刻画非线性动力学特性。为了证明本文方法的一般性及普遍应用价值,在给出其基本理论与分析流程之后, 首先以杜芬系统为例阐述了其在非线性实模态域的应用, 并与用直接积分求解系统方程的结果作了对比;然后通过对干摩擦系统和压电系统的求解与分析分别展示了其在非线性复模态域及多场耦合域的应用;最后给出了基于该理论对大型复杂非线性结构系统求解时的减缩方法。
1 非线性系统的模态分析方法理论线性系统具有模态不变性、模态正交性和叠加性;线性系统的所有模态共同构成了一组模态基,系统的所有解都可以由这些模态的线性叠加组合获得。对于非线性系统来说,线性模态理论中的模态不变性和正交性不再成立。鉴于非线性动力学系统中的非线性力与系统自身运动状态的相关性(在位形空间中依赖于位移或速度),非线性模态理论认为在模态空间里,非线性模态不像线性系统的模态那样与外界因素无关,而是也与外界因素相关;这种相关性,可以通过引入一个随外界因素变化的模态参数来表示。本文选取模态振动幅值(简称模态幅值)作为表征模态与外界因素直接相关的参数。模态幅值的引入意味着非线性振动模态与线性系统模态的本质不同:对于离散系统它不再是一组成比例的数。
1.1 非线性模态理论记系统中的非线性力为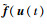
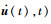
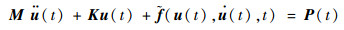
|
(1) |
式中:M为质量矩阵;K为刚度矩阵;P为外激励力;u为位移。
设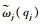
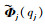
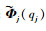
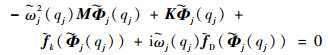
|
(2) |
式(2)意味着在主共振区,方程中的非线性力被分解成了两部分: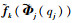
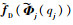
为了求解上述非线性问题,对非线性特征振型关于质量矩阵作归一化处理:

|
(3) |
结合式(2)和式(3),通过牛顿-拉夫逊迭代算法可近似求解该非线性方程,得到以qj为参数的主共振模态的频率和振型。
1.2 非线性模态参数基于1.1节的非线性模态理论,可以提取出一系列表征非线性系统动力学行为的模态参数。类似线性系统,定义如下模态质量、模态阻尼和模态刚度:
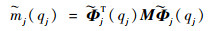
|
(4) |
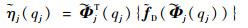
|
(5) |
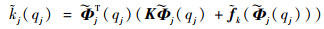
|
(6) |
式中: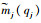
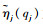
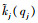
设对应于某一个不变的外界状态(即对应某一个qj),第j阶主共振模态可表示成一系列线性模态振型的组合,假设选取N1阶线性模态Φi来构成该阶非线性模态:
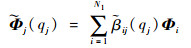
|
(7) |
式中: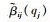
为了便于对系统作模态分析和之后求解系统的强迫响应,可进一步对这些非线性模态参数关于模态幅值的变化做插值处理,构造非线性模态参数关于模态幅值的函数。
1.3 基于单模态共振理论求解系统强迫响应当系统受到外界简谐激励P0cos(ωt)时,设主共振模态响应解的振动频率与激振力频率一致,为ω。

|
(8) |
将式(8)代入非线性微分方程并左乘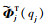

|
(9) |
由1.1节和1.2节已知,对于一个给定的qj,通过求解非线性方程式(2),即可得到模态参数
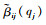
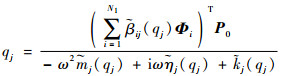
|
(10) |
求得该激励下非线性系统的模态幅值后,再将其代入1.2节中得到的模态参数关于模态幅值的函数关系,很容易求解出系统受到外界简谐激励时对应的单阶主共振模态振型和与之对应的模态参数值,而单阶非线性模态的稳态响应则通过式(11)得到:
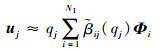
|
(11) |
根据由单模态共振理论发展得到的主共振模态近似法[6-11],最终系统的强迫响应可通过所选取的各单阶非线性模态强迫响应叠加得到,如下:
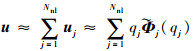
|
(12) |
式中:Nnl为选取的非线性模态阶数。
需要强调的是,这里的非线性模态叠加与线性模态叠加有本质差别。线性系统是基于模态的正交性,首先求出表征系统固有特性的模态(与外激励无关),以模态为正交基构造模态空间,在模态空间求解解耦的受迫振动方程;非线性系统第一不满足模态正交性,第二其模态与外界激励相关;其响应幅值的求解基于主共振模态近似理论,即认为共振区的系统响应可由单阶非线性模态响应近似[6-7]。求解该单阶非线性模态响应时,考虑到非线性模态与系统受激励和响应水平的相关性,需先建立自由振动状态下单阶模态与其模态幅值的函数关系,再代入受迫振动方程迭代计算出特定激励力下的单阶模态幅值和非线性模态,最后代入式(11)和式(12)分别求出单阶非线性模态响应和系统响应。
综上所述,基于非线性模态分析求解系统稳态响应的步骤可以由图 1所示流程图来表示。

|
| 图 1 非线性模态分析求解稳态响应流程 Fig. 1 Flowchart of steady-state response solved by nonlinear modal analysis |
需要指出的是,在计算过程中构成j阶非线性模态的线性模态阶数Nl及非线性模态阶数Nnl不能太小,但也不是越大越逼近精确值;与线性系统不同的是,在大于某一值后其值再增大将不再影响结果精度[4, 13-14]。
上述方法在求解大型复杂非线性系统时极具优势。以谐波平衡法为例,若考虑m阶谐波成分,需要迭代求解mN×mN维非线性矩阵方程才能求解非线性系统的响应。然而应用本文方法在求解系统响应时,依据单模态共振理论,若选取Nnl阶非线性模态来近似表示系统的解,非线性矩阵方程可被解耦成Nnl个N×1维的非线性方程,求解单阶非线性模态响应时分为如下2步:①求解非线性模态,即求解N×1维非线性方程;②求解单阶主共振模态对应的模态幅值,求解标量形式的单变量非线性方程,由此大大减少了计算时间和计算机所需内存。
除了能获得非线性系统的稳态响应之外,本文方法还能通过非线性模态参数,从模态角度分析系统的非线性特性,总结非线性系统的振动特性和非线性行为特征。
2 在非线性实模态域的应用为了验证本文方法的合理性,首先用该方法求解了杜芬系统,并将结果与直接积分求解杜芬方程的结果进行对比。
2.1 多自由度杜芬系统的求解杜芬系统是一种同时具有线性刚度与立方刚度的系统。单自由度杜芬振子模型由Duffing[15]最早提出,Duffing及后人基于此模型研究总结了很多非线性系统的典型特性。在数值方法充分发展的今天,杜芬系统经常用于检验新算法的功效。
受激振力频率为ω的简谐激励的无阻尼杜芬系统的运动微分方程为
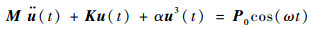
|
(13) |
根据第1节所介绍的理论和方法,对式(13)求解时,先借助非线性模态理论求得非线性模态,再计算单阶主共振模态对应的谐波激励下系统的响应,最后对选取的单阶主共振模态对应的稳态响应做叠加,从而得到系统的稳态响应。由于是无阻尼系统,应用迭代算法求解该方程时仍在实数空间里。
将单阶非线性共振模态对应的系统响应表示为

|
(14) |
再将式(14)代入杜芬系统方程,可得

|
(15) |
若忽略三阶以上谐波成分的影响,仅考虑主谐波成分,可得系统的模态空间运动微分方程为
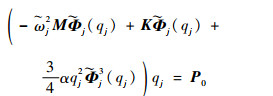
|
(16) |
杜芬系统的非线性模态刚度为

|
(17) |
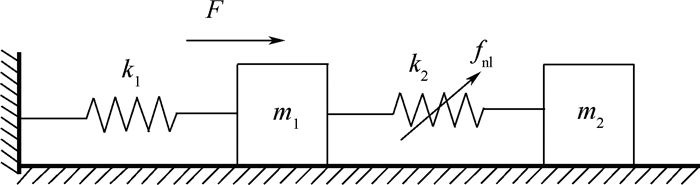
本节通过对一个包含杜芬振子的二自由度参数模型(见图 2)的具体求解,展示第1节中描述的非线性模态分析方法的可行性和有效性,并通过与在时域直接积分获得的结果比较,验证其正确性。
|
| 图 2 二自由度非线性参数模型 Fig. 2 2-DOF nonlinear parametric model |
图 2所示参数模型采用无量纲参数,振子质量分别为m1=1、m2=1,弹簧刚度分别为k1=600、k2=400。振子m1受简谐激振力作用,当用其模拟旋转机械的偏心力时,激振力表达式为:F=A0mrω2cos(ωt),m为偏心质量,r为偏心半径,取mr=0.01,A0为激振力幅值,取A0=0.03。在2个质量块m1和m2之间引入杜芬振子,立方项系数为α=1×108。为避免计算过程中共振区出现数值溢出问题,在计算时引入阻尼系数为0.5%的微小黏滞阻尼。则该系统对应的数值求解方程为
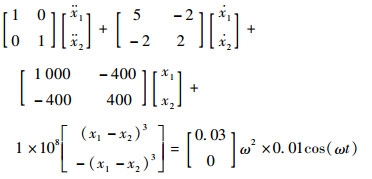
|
(18) |
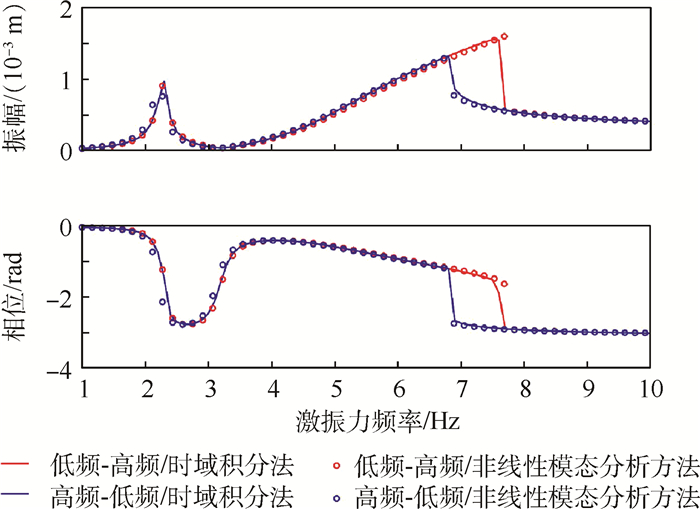
将第1节中描述的非线性模态理论应用于计算该杜芬非线性系统的强迫响应,并与龙格库塔时域积分法计算得到的频响曲线进行比较,m1和m2的响应比较曲线分别如图 3和图 4所示。
|
| 图 3 针对杜芬系统采用时域积分法和非线性模态分析方法计算m1的频响曲线 Fig. 3 Frequency response curves of m1computed by time-domain integration method and nonlinear modal analysis method for Duffing system |

|
| 图 4 针对杜芬系统采用时域积分法和非线性模态分析方法计算m2的频响曲线 Fig. 4 Frequency response curves of m2 computed by time-domain integration method and nonlinear modal analysis method for Duffing system |
由图 3和图 4可知,非线性模态分析方法与时域积分法得到的频响曲线吻合良好,由此验证了非线性模态分析方法的准确性。上述结果表明,不论是m1还是m2,均在第二阶共振频率附近表现出了较强的非线性特征,出现了典型的跳跃现象,蓝线和红线错位区为不稳定区域。
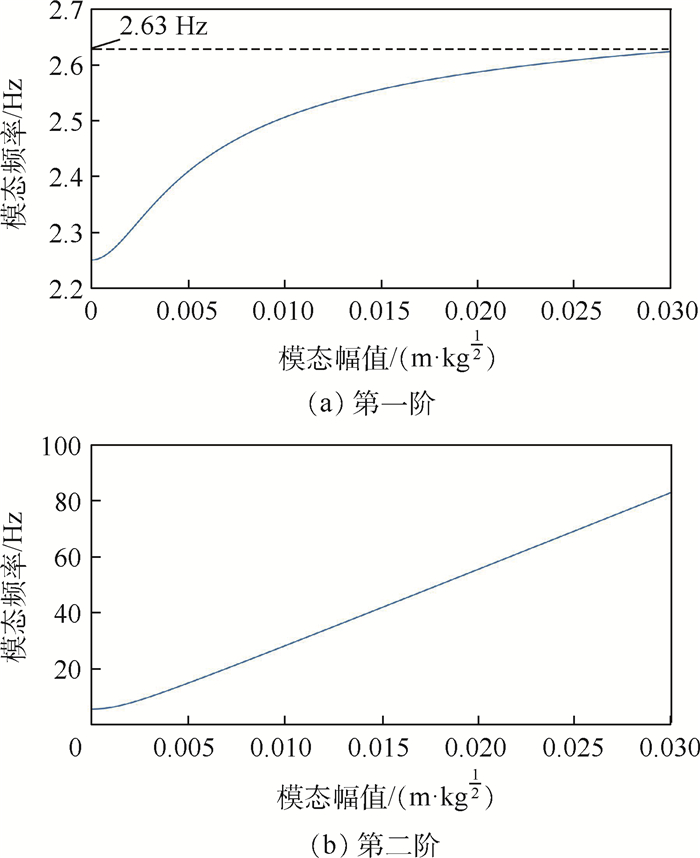
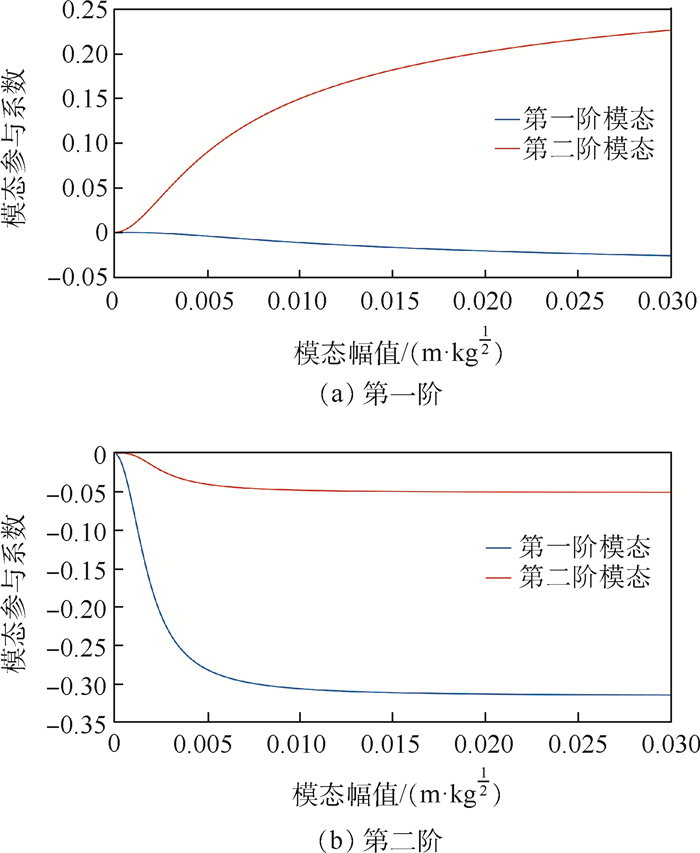
在用非线性模态分析方法求解的同时,还获得了有助于分析非线性系统动力学特征的模态参数。非线性模态频率和表征模态振型的模态参与系数随非线性模态幅值的变化规律分别如图 5和图 6所示。
|
| 图 5 杜芬系统的两阶非线性模态频率随模态幅值的变化 Fig. 5 Variation of nonlinear modal frequency with modal amplitude for the two modes of Duffing system |
|
| 图 6 杜芬系统的两阶模态参与系数随模态幅值的变化 Fig. 6 Variation of modal participation factor with modal amplitude for the two modes of Duffing system |
通过分析图 5中2个模态频率的变化趋势,观察到第一阶从2.25 Hz逼近2.63 Hz趋近稳定,第二阶则从5.5 Hz开始不断增大,最后呈发散趋势,可初步得出第二阶共振频率非线性更强的结论。另外,通过比较图 6中两阶模态的模态参与系数,第一阶为0.25小于第二阶0.35,说明第一阶非线性模态与第一阶线性模态的相关性更大,且随着模态幅值的增加,相关性相应增加。第二阶非线性模态与第一阶和第二阶线性模态均有相关性,且随着模态幅值的增加,与两阶线性模态的相关性均增加。另外,通过分析模态参与系数随模态幅值的变化率可知,第二阶非线性模态表现出更强的非线性。同样地,也可得出第二阶模态非线性较强的推论。
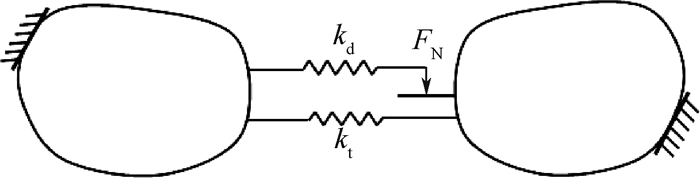
3 在非线性复模态域的应用 3.1 具有干摩擦阻尼的振动系统干摩擦阻尼不受温度限制、结构简单、减振效果明显,且经济性好,这些优势使其成为航空发动机结构部件最主要的减振方式[16]。干摩擦阻尼由接触面之间的相对运动产生,图 7给出一种描述干摩擦阻尼器的力学模型[11]。图中:kt为接触面之间的接触静刚度,kd为接触面产生相对滑移之前的线性动刚度,接触面上的滑动摩擦因数为μd,正压力为FN。由干摩擦产生的非线性运动阻力不仅与接触面之间的相对位移有关,还与相对运动方向有关,因此,干摩擦阻尼器既具有刚度效应,又包含阻尼效应。
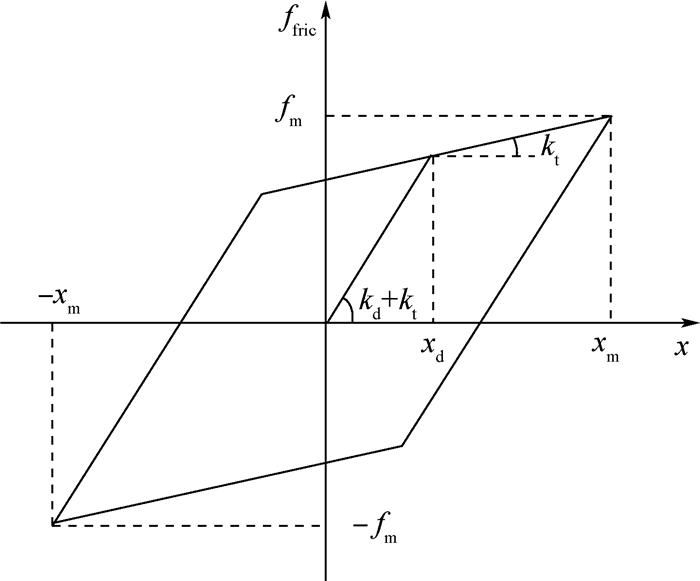
刻画干摩擦力与位移的关系的模型有多种,最常用的是根据Masing法则建立的双线性迟滞模型[17],如图 8所示。该模型代表了系统振动一个稳定周期内摩擦力的变化规律,现以前四分之一周期为例说明。当接触面之间的相对位移从0增加xd的过程中,两接触面之间的相对运动表现出黏滞特性;当相对位移突破xd这个特征位移时,相对运动出现宏观滑移特性。上述过程中,接触面上摩擦力大小随相对位移的变化为

|
(19) |
式中:特征位移xd与线性动刚度kd、接触面上的滑动摩擦因数μd和正压力FN相关,满足:xd=μdFN/kd。
Masing法则的表述为:若初始加载过程中摩擦力和相对位移满足如下函数关系:
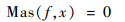
|
(20) |
则基于Masing法则构造的迟滞环曲线满足:

|
(21) |
基于上述干摩擦模型的干摩擦力对系统的刚度和阻尼均有贡献,因此对于一个稳定周期,可将摩擦力在复域空间表示为
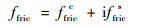
|
(22) |
为了说明非线性模态分析方法在复模态域中的应用,沿用如图 2所示的二自由度参数模型,仅将其中的非线性刚度(杜芬刚度模型)用干摩擦(双线性迟滞环)模型替代(假设系统中存在干摩擦阻尼器),系统的质量和刚度矩阵保持不变,外界激励形式不变,激振力幅值取A0=3;此系统中干摩擦为主要阻尼,但为了避免计算中出现数值溢出问题,仍在求解过程中引入了阻尼因子为0.05%的极微弱黏滞阻尼。双线性迟滞环模型参数kd=200、kt=0.2,接触面上的滑动摩擦因数取μd=0.5,正压力取FN=15 N。该系统对应的数值求解方程与式(18)相比,仅在激振力幅值和非线性力这2项上有差异,其中激振力幅值从0.03 N变为3 N,非线性力从三次项变为由式(22)确定的干摩擦力。
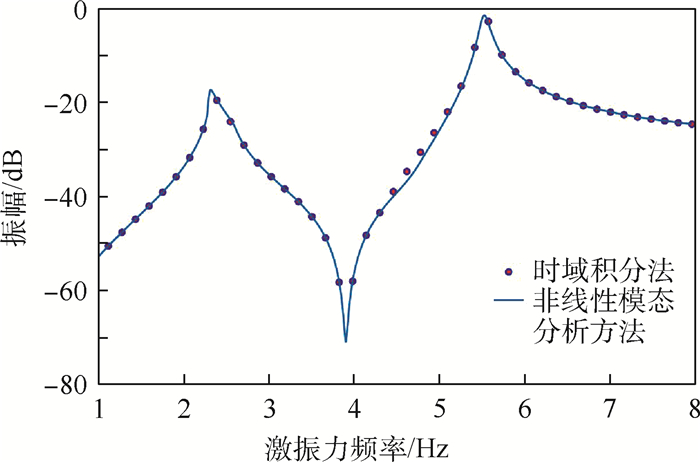
当系统中的非线性力同时包含刚度项和阻尼项时,其运动方程中包含了复数项,对应的数值求解问题转化为复域的求解问题,此处需注意将方程中的未知量设为复变量进行分析。根据非线性模态理论和纽马克时域积分法计算的2个质量块的频响幅值对比曲线分别如图 9和图 10所示。同时给出数值积分的结果,目的在于对非线性复模态分析计算结果的正确性进行校核。
|
| 图 9 针对干摩擦系统采用时域积分法和非线性模态分析方法计算m1的频响曲线 Fig. 9 Frequency response curves of m1computed by time-domain integration method and nonlinear modal analysis method for dry friction system |
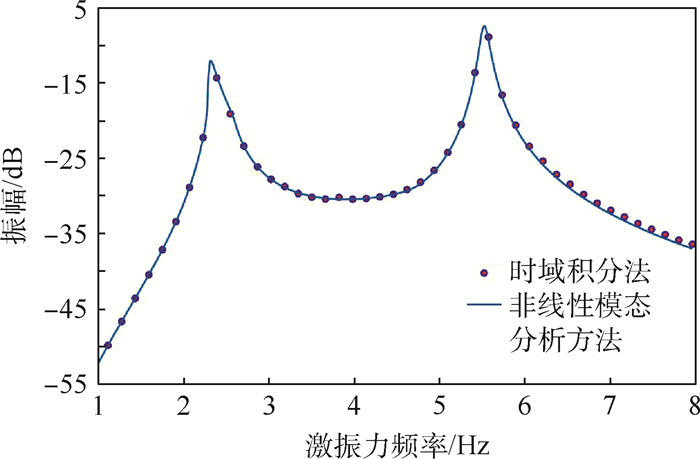
|
| 图 10 针对干摩擦系统采用时域积分法和非线性模态分析方法计算m2的频响曲线 Fig. 10 Frequency response curves of m2computed by time-domain integration method and nonlinear modal analysis method for dry friction system |
由图 9和图 10可知,非线性模态理论分析带有干摩擦阻尼器的隐式非线性系统同样有效,与时域积分法相比,速度快而不损失计算精度。因此,可根据非线性模态分析方法,快速求出不同正压力下的系统位移随激振力频率的变化曲线,如图 11和图 12所示,其中正压力取0, 5, 15, 55, 105, 2 000 N。对于质量块m1和m2来说,第一阶共振频率附近的最优控制正压力均值为15 N,而第二阶共振频率附近的最优控制正压力均值为55 N。

|
| 图 11 不同正压力下m1的频响曲线 Fig. 11 Frequency response curves of m1 under different normal pressure |

|
| 图 12 不同正压力下m2的频响曲线 Fig. 12 Frequency response curves of m2 under different normal pressure |
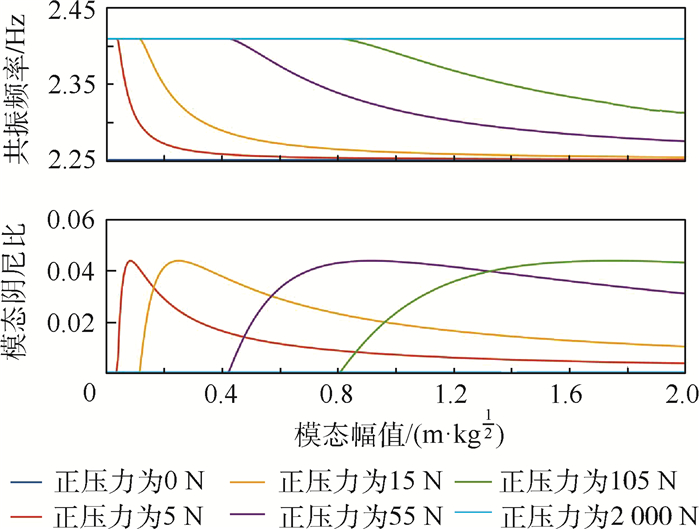
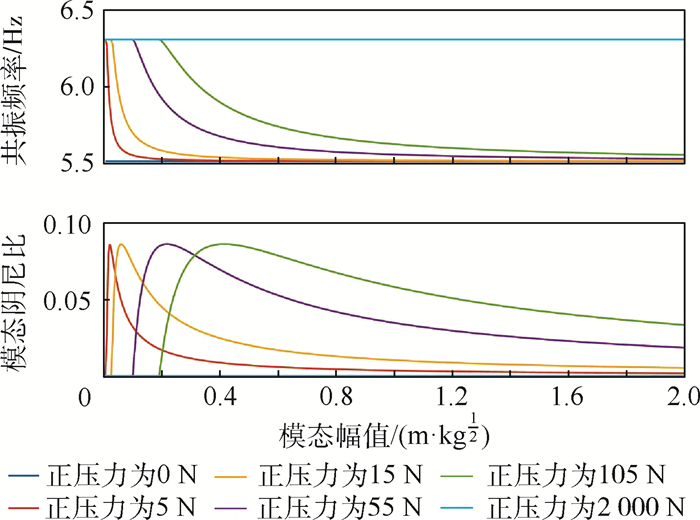
除此之外,在基于非线性模态理论计算频响曲线时,还得到了系统的共振频率和干摩擦模态阻尼比随模态幅值的变化曲线,如图 13和图 14所示。如此就可以从模态的角度去分析系统的非线性特性。可以看到,当模态幅值增大时,第一、二阶共振区的频率均呈下降趋势;第一阶共振区的频率从2.42 Hz降到2.25 Hz,第二阶共振区的频率从6.3 Hz降到5.5 Hz;其中2.42 Hz和6.3 Hz分别对应干摩擦阻尼器的接触面处于黏滞状态的系统二阶固有频率,即m1和m2间刚度为k2+kd+kt的情况;2.25 Hz和5.5 Hz对应干摩擦阻尼器的接触面处于自由振动状态的系统二阶固有频率,即m1和m2间刚度为k2+kt的情况;另外,两阶模态的干摩擦模态阻尼比均从零开始,达到最大值,然后减小,第一阶模态阻尼比最大值为0.04,第二阶模态阻尼比为0.08,均远大于结构中引入的黏滞阻尼0.05%,由此可知干摩擦阻尼起主导作用;且第二阶干摩擦阻尼比大于第一阶,若观察图 9和图 10中的频响曲线,可知第二阶共振区响应确实得到了更好的抑制。
|
| 图 13 第一阶共振频率附近,不同正压力下的非线性共振频率和干摩擦模态阻尼比随模态幅值的变化 Fig. 13 Variation of nonlinear resonance frequency and dry friction modal damping with modal amplitude under different normal pressure for the first order mode |
|
| 图 14 第二阶共振频率附近,不同正压力下的非线性共振频率和干摩擦模态阻尼比随模态幅值的变化 Fig. 14 Variation of nonlinear resonance frequency and dry friction modal damping with modal amplitude under different normal pressure for the second order mode |
压电材料是应用非常广泛的智能材料之一。当压电材料在特定方向上受到力的作用时,会在垂直于力的电极上出现正负相反的束缚电荷,这种现象称为压电效应;相反,在压电材料电极上施加电压时,压电材料会发生弹性形变,这种现象称为逆压电效应。基于压电效应的减振技术近年来得到了极大发展,其中基于压电材料的同步开关阻尼技术是一个前沿性的且具有广阔应用前景的半主动减振技术。
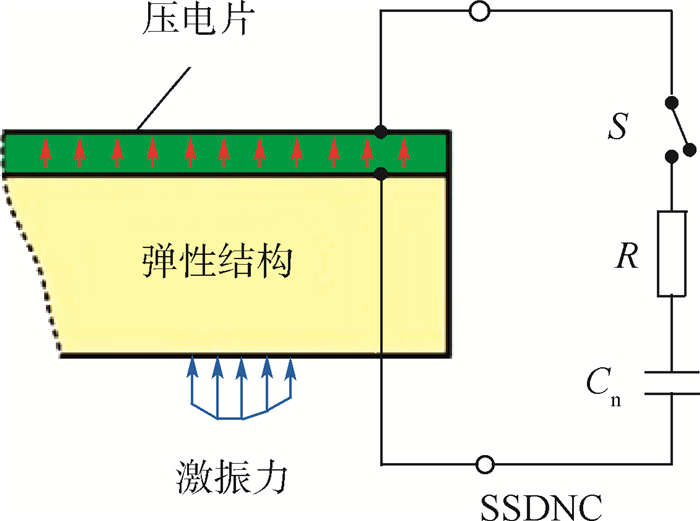
压电同步开关半主动减振技术的基本原理为:在弹性结构表面粘贴压电片(见图 15[5]),将同步开关电路与压电片的2个电极相连,控制好开关开启与闭合的时间即可以使压电材料产生一个始终阻碍弹性结构变形的力,因此形成的阻尼称为(压电)同步开关阻尼(Synchronized Switch Damping,SSD);如果再将此电路与一个负电容电路串联,可以大大提高机电转换的效率,由此形成的压电阻尼称为基于负电容电路的同步开关阻尼(Synchronized Switch Damping based on Negative Capacitor, SSDNC)[5]。
根据SSD的原理,在结构振动位移达到最大时电路开关闭合,此时压电片电极电压Vm与结构位移幅值xM之间的关系为[16]
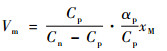
|
(23) |
式中:αp为压电片的力系数,表示压电片在单位电压下产生的力的大小,一般通过实验方法获得αp的大小;Cp为压电片的内置电容;Cn为电路中的负电容。忽略开关的闭合时间,可得SSDNC电路的电压表达式为

|
(24) |
式中:χC为电路中负电容值的大小与压电片内置电容值之比,表示为

|
(25) |
由压电材料本构关系可以推导出压电片对结构的机电耦合作用力fc(t)与SSD电路中压电片
电极电压VSSD(t)之间的关系为
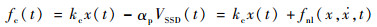
|
(26) |
式中:kc为压电片的机械刚度,代表压电同步开关阻尼力。
式(24)、式(26)表明,电压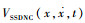
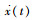
为了展示非线性模态分析方法在耦合系统分析中的可行性和有效性,仍沿用如图 2所示的二自由度参数模型,仅将其中的非线性刚度(杜芬刚度模型)用SSD模型(式(24)和式(26))替代。模型参数为:电容比χC=0.9,机电耦合系数γp=α2p/Cp=0.01,m1=1,m2=2,k1=1,k2=0.4,压电片的机械刚度kc=0.05,外界激励形式不变,激振力幅值取A0=1;此外在系统中引入了微小的瑞利阻尼,质量项比例系数为1×10-10,刚度项比例系数为0.02。则该系统对应的数值求解方程为

|
(27) |
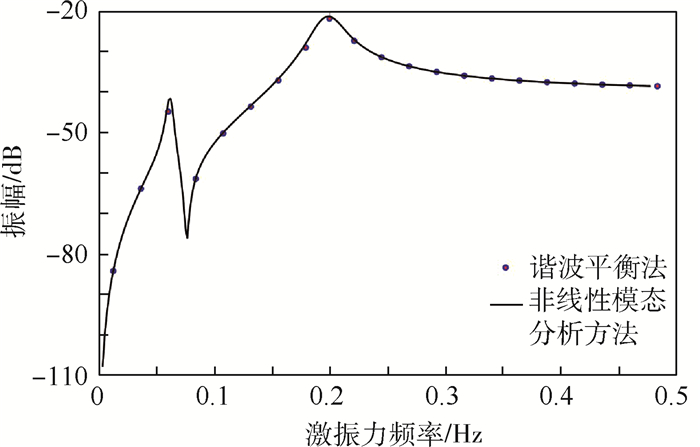
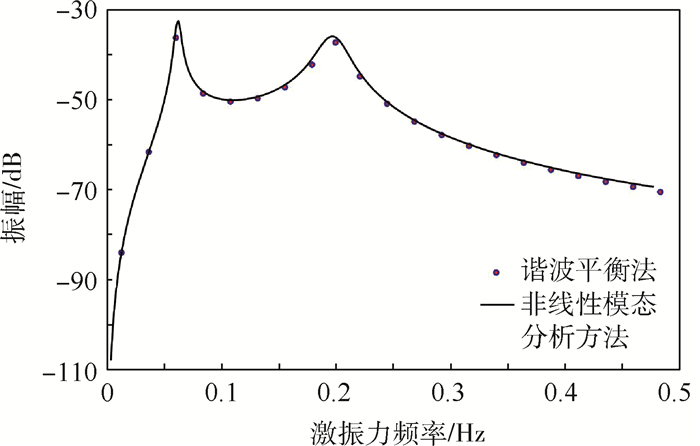
根据非线性模态理论和谐波平衡法计算2个质量块的频响幅值对比曲线分别如图 16和图 17所示。同时给出谐波平衡法的结果,目的在于对非线性模态分析方法用于耦合系统的计算结果的正确性进行校核。
|
| 图 16 谐波平衡法和非线性模态分析方法计算m1的频响曲线 Fig. 16 Frequency response curves of m1 computed by harmonic balance method and nonlinear modal analysis method |
|
| 图 17 谐波平衡法和非线性模态分析方法计算m2的频响曲线 Fig. 17 Frequency response curves of m2 computed by harmonic balance method and nonlinear modal analysis method |
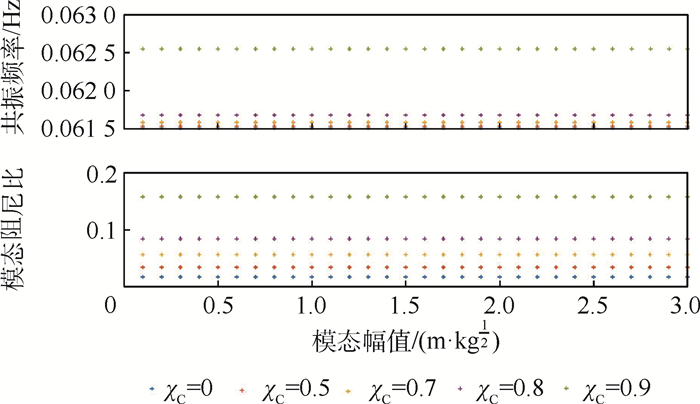
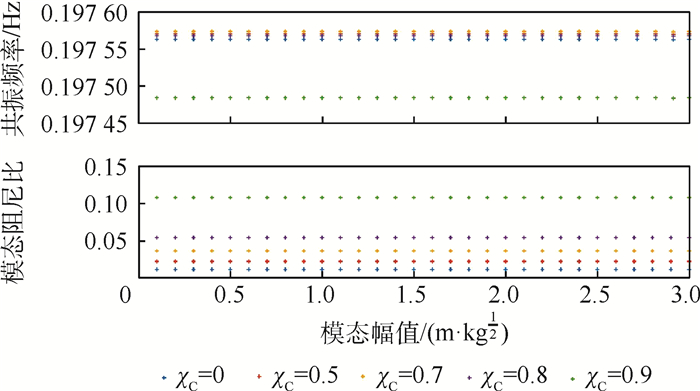
在非线性模态分析过程中得到的两阶模态特性如图 18和图 19所示,可以观察到,虽然SSD是非线性的,但具有该阻尼的系统却具有线性系统的特性,即模态频率和模态阻尼比并不随自由振动状态下的模态幅值发生变化,这意味着系统参数的设计可以独立于激励水平。
|
| 图 18 第一阶共振频率附近,不同电容比下的非线性共振频率和模态阻尼比随模态幅值的变化 Fig. 18 Variation of nonlinear resonance frequency and modal damping with modal amplitude under different capacitance ratios for the first order mode |
|
| 图 19 第二阶共振频率附近,不同电容比下的非线性共振频率和模态阻尼随模态幅值的变化 Fig. 19 Variation of nonlinear resonance frequency and modal damping with modal amplitude under different capacitance ratios for the second order mode |
工程实际中的交通工具、航空航天器等大型复杂结构系统均由众多子结构组成,为了抑制结构振动,往往在子结构连接面上引入阻尼材料或结构,而这些具有减振作用的材料或结构在刚度和阻尼特性上通常都是非线性的。线性振动系统分析中的模态综合法将大型复杂结构系统划分为若干子结构,独立分析各子结构的模态,根据目标频率范围对模态作适当的截断,仅保留各子结构的低阶模态,通过物理-模态坐标转换将物理空间自由度化为模态空间缩聚自由度,从而使计算规模大大减小,提高计算效率,节省大量计算时间。本节基于非线性模态理论,给出将模态综合法推广到具有非线性连接界面的大型复杂非线性系统的方法。
线性模态综合法按子结构界面的处理方式可分为固定界面、自由界面和混合界面三大类,主要不同之处在于选取的位移近似表达式及构造的物理-模态坐标转换矩阵。下面按照经典的固定界面模态综合法(即Craig-Bampton方法)[18],针对界面的处理方式及基本思想,论述基于非线性模态理论的减缩方法。
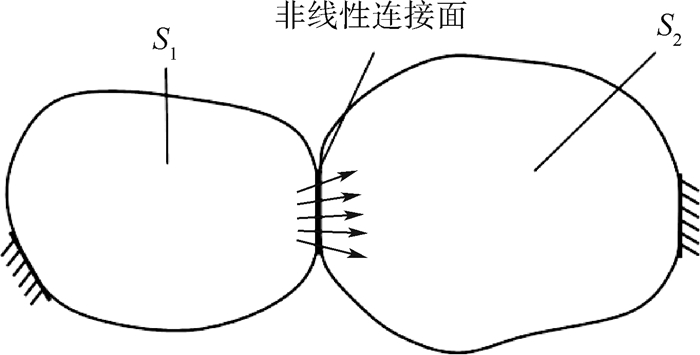
不失一般性,以2个子结构(S1, S2)和两者间的非线性连接面(J)组成的系统(见图 20)为例,论述此类结构系统的减缩方法。
|
| 图 20 由两个子结构和非线性连接面组成的系统简图 Fig. 20 Illustration of an assembled system with a nonlinear interface and two substructures |
首先求解各子结构对应的固定界面模态矩阵ΦS1和ΦS2,即当各子结构的界面自由度被固定时,子结构S1和S2的模态振型由解如下特征值问题获得:

|
(28) |
式中:MS1和KS1分别为不包含界面自由度的子结构S1的质量和刚度矩阵;ΛS1和ΦS1分别为方程的特征值向量和特征向量矩阵。
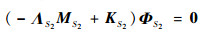
|
(29) |
式中:MS2和KS2分别为子结构S2的质量和刚度矩阵;ΛS2和ΦS2分别为方程的特征值向量和特征向量矩阵。
为了修正施加固定边界约束造成的计算误差,引入由连接面上的自由度单位位移引起的子结构变形,也称作静力约束模态,如下:

|
(30) |

|
(31) |
式中:ΨJ=IJ为单位矩阵,其物理意义是保留连接面上自由度的所有模态信息,不作任何模态截断,模态坐标即为物理坐标;ΨS1J为连接界面J位移引起的S1内部位移;ΨS2J为连接面位移引起的S2内部位移。
修正过后的子结构和界面位移表达式为
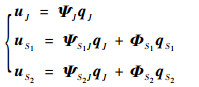
|
(32) |
基于Craig-Bampton方法的物理-模态坐标转换矩阵为
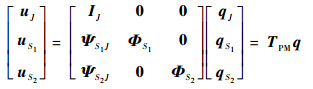
|
(33) |
式中:qJ为界面分支模态位移;qS1为子结构S1的模态位移;qS2为子结构S2的模态位移;TPM为物理-模态坐标转换矩阵,为一个N×Nr的矩阵,Nr < < N。物理空间位移向量u为N×1维的向量,包含NS个子结构内部自由度和NJ个界面自由度,N=NJ+NS;在物理-模态坐标转换过程中,保留所有连接面自由度(数目为NJ),对各子结构的固定界面模态作截断,仅保留NSr阶低阶主模态信息,Nr=NJ+NSr,且NSr < < NS,故有:Nr < < N。最终经过物理-模态坐标转换的运动方程矩阵形式为
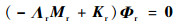
|
(34) |
式中: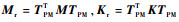
基于如上减缩模型,应用非线性模态理论分析其动力学特征;减缩非线性模态分析方法的具体实施步骤如下:
步骤1 建立系统的完整有限元离散模型:

|
(35) |
式中:D为阻尼矩阵。
步骤2 选取合适的减缩方法,将系统的完整有限元模型从物理空间转换到模态空间,保留子结构中低阶主模态进行模态截断:
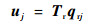
|
(36) |
步骤3 根据单模态共振理论和利兹-伽辽金映射方法,建立非线性减缩模型在模态空间的自由振动方程:
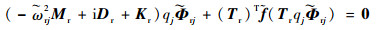
|
(37) |
步骤4 基于Bogolyubov线性等价原理[19],利用数值方法求解上面的减缩问题,通过迭代算法求出减缩模型的主共振非线性模态: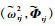
步骤5 基于步骤4中得到的主共振非线性模态坐标随其模态幅值的变化规律,提取表征非线性动力学行为的模态参数,建立这些模态参数与模态幅值间的函数关系,并作曲线拟合。
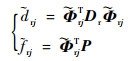
|
(38) |
步骤6 基于步骤5建立的非线性模态参数与模态幅值间的函数关系,利用数值方法迭代求解受到外界激励时该主共振模态对应的模态幅值:
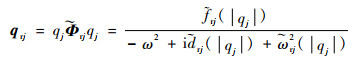
|
(39) |
步骤7 将模态坐标映射到物理空间,得到该阶模态对应的稳态响应:

|
步骤8 对各阶非线性主共振模态计算得到的响应结果作叠加得到系统的稳态响应:

|
(40) |
该减缩模态算法应用在模态间弱耦合的非线性系统上时能得到准确的结果,有关此方面的研究还在发展之中,笔者已针对包含有杜芬、干摩擦阻尼和SSD非线性的复杂系统做了初步尝试,具体应用实例可参见文献[4, 13-14]。
6 结论1) 本文基于非线性模态理论的研究进展,针对大型复杂非线性结构系统的分析问题提炼了一套基于单模态共振理论和非线性模态理论的计算方法。
2) 给出的杜芬系统和干摩擦系统的算例表明了本文方法对于求解强非线性系统的适用性——对于模态间弱耦合(主共振模态相对稀疏)的系统具有通用性;通过对具有非线性压电阻尼系统的分析算例进一步表明了本文方法对于求解非线性系统具有普适性。
3) 针对大型复杂结构系统,本文提出将上述论证的方法与模态综合法结合的思想,并给出了具体实施步骤,其特点在于:基于此方法、步骤不仅可以快速求得系统的稳态响应,还能得到一组表征系统非线性动力学特性的模态参数(如模态频率、模态阻尼和模态参与系数),通过分析这些模态参数随系统模态幅值的变化规律,有助于理解系统的非线性动力学行为。
| [1] |
JIANG D, PIERRE C, SHAW S W. Nonlinear normal modes for vibratory systems under harmonic excitation[J]. Journal of Sound and Vibration, 2005, 288(4-5): 791-812. DOI:10.1016/j.jsv.2005.01.009 |
| [2] |
TOUZÉ C, AMABILI M. Nonlinear normal modes for damped geometrically nonlinear systems:Application to reduced-order modelling of harmonically forced structures[J]. Journal of Sound and Vibration, 2006, 298(4-5): 958-981. DOI:10.1016/j.jsv.2006.06.032 |
| [3] |
RENSON L, KERSCHEN G, COCHELIN B. Numerical computation of nonlinear normal modes in mechanical engineering[J]. Journal of Sound and Vibration, 2016, 364: 177-206. DOI:10.1016/j.jsv.2015.09.033 |
| [4] |
HUANG X R, JÉZÉQUEL L, BESSET S, et al. Nonlinear hybrid modal synthesis based on branch modes for dynamic analysis of assembled structure[J]. Mechanical Systems and Signal Processing, 2018, 99: 624-646. DOI:10.1016/j.ymssp.2017.07.002 |
| [5] |
LIU J Z, LI L, HUANG X R, et al. Dynamic characteristics of the blisk with synchronized switch damping based on negative capacitor[J]. Mechanical Systems and Signal Processing, 2017, 95: 425-445. DOI:10.1016/j.ymssp.2017.03.049 |
| [6] |
ROSENBERG R M. The normal modes of nonlinear n-degrees-of-freedom systems[J]. Journal of Applied Mechanics, 1962, 29(1): 595-611. |
| [7] |
SZEMPLINSKA-STUPNICKA W. The resonant vibration of homogeneous non-linear systems[J]. International Journal of Non-Linear Mechanics, 1980, 15(4-5): 407-415. DOI:10.1016/0020-7462(80)90026-8 |
| [8] |
JÉZÉQUEL L, LAMARQUE C. Analysis of non-linear dynamical systems by the normal form theory[J]. Journal of Sound and Vibration, 1991, 149(3): 429-459. DOI:10.1016/0022-460X(91)90446-Q |
| [9] |
SETIO H D, SETIO S, JÉZÉQUEL L. A method of non-linear modal identification from frequency response tests[J]. Journal of Sound and Vibration, 1992, 158(3): 497-515. DOI:10.1016/0022-460X(92)90421-S |
| [10] |
CHONG Y H, IMREGUN M. Development and application of a nonlinear modal analysis technique for mdof systems[J]. Journal of Vibration and Control, 2001, 7(2): 167-179. DOI:10.1177/107754630100700202 |
| [11] |
GIBERT C. Fitting measured frequency response using non-linear modes[J]. Mechanical Systems and Signal Processing, 2003, 17(1): 211-218. |
| [12] |
郑兆昌. 关于线性和非线性系统内在的本质联系——多自由度非线性系统的定量和定性分析[J]. 振动与冲击, 2008, 27(1): 4-8. ZHENG Z C. Intrinsic and simple connection of linear systems with non-linear ones:Quantitative and qualitative analysis of large scale multiple DOF nonlinear systems[J]. Journal of Vibration and Shock, 2008, 27(1): 4-8. DOI:10.3969/j.issn.1000-3835.2008.01.001 (in Chinese) |
| [13] |
HUANG X R, JÉZÉQUEL L, BESSET S, et al. Nonlinear modal synthesis for analyzing structures with a frictional interface using a generalized Masing model[J]. Journal of Sound and Vibration, 2018, 434: 166-191. DOI:10.1016/j.jsv.2018.07.027 |
| [14] |
LIU J Z, LI L, FAN Y, et al. A modified nonlinear modal synthesis scheme for mistuned blisks with synchronized switch damping[J]. International Journal of Aerospace Engineering, 2018, 2018: 8517890. |
| [15] |
DUFFING G. Elastizität und Reibung beim Riementrieb[J]. Forschung Auf Dem Gebiet Des Ingenieurwesens A, 1931, 2(3): 99-104. |
| [16] |
李琳, 刘久周, 李超. 航空发动机中的干摩擦阻尼器及其设计技术研究进展[J]. 航空动力学报, 2016, 31(10): 2305-2317. LI L, LIU J Z, LI C. Review of the dry friction dampers in aero-engine and their design technologies[J]. Journal of Aerospace Power, 2016, 31(10): 2305-2317. (in Chinese) |
| [17] |
CHIANG D Y. The generalized Masing models for deteriorating hysteresis and cyclic plasticity[J]. Applied Mathematical Modelling, 1999, 23(11): 847-863. DOI:10.1016/S0307-904X(99)00015-3 |
| [18] |
BAMPTON M C C, CRAIG R R. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7): 1313-1319. DOI:10.2514/3.4741 |
| [19] |
KRYLOV N M, BOGOLYUBOV N N. Introduction to non-linear mechanics[M]. Princeton: Princeton University Press, 1947.
|