随着航空业的不断发展, 飞机的应用也从早期的军事用途逐渐扩展到飞行表演、紧急救援、商业运输等多个领域。这就要求飞机可以适应各种复杂气象条件完成预定飞行任务[1]。
飞机结冰现象主要发生在飞行中遇到含有过冷水滴的云层时,过冷水滴撞击到机体迎风表面就有可能发生结冰现象[2]。通过研究发现,结冰对飞机的影响一方面是结冰后飞机覆冰会造成气动外形破坏,形成的表面粗糙度会改变飞机的的原有流场状态,从而造成阻力增加、升力减小、飞行稳定性降低等; 另一方面还会造成仪表失灵,引发飞行员错误操作,严重时可能导致坠机[1]。
随着计算机领域的飞速发展,研究及预测结冰问题已经可以利用数值方法来完成结冰模拟。然而利用数值手段模拟结冰问题需要分别得到机翼绕流流场和过冷水滴流动情况以及求解结冰热力学方程[3],因此结冰模拟也是比较复杂的, 对于数分钟的结冰过程通常需要较长时间才能得到模拟结果。
目前有2个因素需要开展结冰冰形快速预测方法研究。一方面,适航认证结冰试飞过程中,需要针对各个飞行状态的结冰情况实时预测其对性能的影响,从而判断防除冰系统的开启[4];另外即便现有飞机防冰系统已经比较完善, 但除防冰系统并不能在各种状态下都达到理想的效果, 很多情况下依然需要带冰飞行,考虑在设计阶段就讨论结冰情况的影响,在保证干净翼型气动性能的同时,提升结冰条件下翼型的气动性能的容冰优化设计很有必要。另一方面,考虑优化设计过程反复迭代时也需要发展快速预测不同外形的不同结冰条件下结冰冰形的方法。因此本文拟根据容冰优化设计需要,建立基于本征正交分解(POD)的结冰冰形快速预测降阶模型。
考虑到飞机结冰问题的高度非线性,以及结冰数值模拟的时间成本,直接对CFD计算原始样本数据进行建模构建代理模型需要较大的样本数目来保证模型的精度,而降阶模型在保证模拟精度同时可以快速预测结果。因此如果利用相关数据处理方法对样本数据进行降阶处理,在低阶空间内对样本数据进行建模会取得更为高效的效果。
降阶模型是利用复杂的数学工具对大型复杂问题进行低阶空间重构,将问题简化为低阶空间元素的线性组合,目前已经有Krylov子空间方法[5]、小波分析[6]、双正交小波[7]和POD[8]等方法。POD方法基本原理[9]是利用已有样本集提取一系列正交基向量,原样本空间可以由这些向量的线性叠加来描述。然后便可以根据所需要的精度舍弃一些低能量模态,从而形成低阶子空间,可以快速进行样本空间重建,因此POD方法可以应用于快速预测飞机结冰冰形以及评估气动性能损失。Nakakita等[10]首先将POD方法应用于飞机结冰冰形预测,并取得了较好的效果,但其采用的插值基于Akima插值法只能应用于两参数情形。
本文介绍了建立基于POD方法和Kriging模型的翼型结冰冰形预测降阶模型方法。首先,详细介绍飞行迎角变化时的降阶模型预测结冰冰形的实现步骤;然后,对结冰试飞认证框架下的五参数的冰形计算结果进行分析,将降阶模型预测的冰形结果与CFD模拟得到的结果进行比较,分析验证预测方法的可靠性;最后,进一步提出了基于更为先进的贝叶斯框架下的Blind-Kriging模型的改进预测模型的方法,建立了降阶模型对结冰冰形进行预测,可以快速、准确地得到样本空间内的任意非样本点冰形。
1 基本方法建立降阶模型通常首先需要完成初始空间采样,然后对样本数据降阶分析,最后完成数据插值等过程。具体流程如图 1所示。

|
| 图 1 降阶模型建立流程 Fig. 1 Reduced order model building process |
对于优化设计而言,合理的参数空间采样是构建代理模型的关键,即采样需要选择合适的试验设计方法。试验设计概念最早是由英国生物统计学家Fisher于20世纪20年代所提出的[11],目前已经发展了许多不同的方法和技术,比如基于拉丁超立方抽样(LHS)方法、Halton序列方法、最小差异序列方法、质心Voronoi镶嵌等。
LHS方法是由Mckay等[12]在1979年提出的试验设计方法,该方法的基本原理是:如果需要得到n个样本点,则利用m个设计变量将参数空间均匀划分为等概率的n个区间,这样整个参数设计空间被分为nm个小区间,然后对其进行n次取样。设计空间抽样时一方面需要保证样本点在每个小区间上都是随机选取的;另一方面需要各个样本点在任一维度上进行投影,每个小区间中只会有一个样本[12]。通常取样的算法为
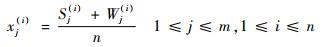
|
(1) |
式中:i为样本点,j为参数的维数,则xj(i)表示第i个样本点的第j维的x;W为[0, 1]之间的随机数;S为0, 1,…, n-1的随机序列。当样本点分布区间不为[0, 1],而是[aj, bj]时,则需要进行拉伸变换:
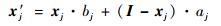
|
(2) |
其中: I为单位向量。抽样具有随机性,因此LHS选取的样本有的分布很好,有的分布很差。该方法有很多改进方法,包括中心化LHS、最优LHS[13]等。MATLAB的LHS已经实现了基于极大极小准则的最优LHS,因此本文采用该试验设计方法,并将试验点均放在小立方体的中心。
1.2 POD方法POD方法是基于物理场原始数据快速准确地重构物理场,同时也可预测物理场在某些未知位置的数据的一种数值方法。POD方法的核心思想是利用特殊正交基函数的迭加来实现参数的近似[14]。它最初主要用于湍流拟序结构的分析研究中,POD如今已成功地应用于各类领域,如机器学习中的主成分分析(Principal Components Analysis, PCA)法,海洋学和气象学中的经验正交函数法,心理学和经济学中常用的要素分析法等[15]。
POD的基本理论[16]为假设存在这样的物理场y=y(x, t), 在某个空间可以表示为如式(3)所示无穷级数:
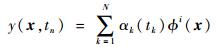
|
(3) |
式中:tn为参数变量,当前研究中可以为速度、压强、升力、阻力、冰形坐标等;αk(tk)为经验系数;ϕi(x)为特征基函数。
利用相关的数学理论将式(3)求解转换为求特征值问题:
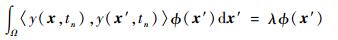
|
(4) |
式中:〈〉为内积运算符。对于此问题直接求解需要消耗巨大的资源和时间,所以实际应用中常采用由Sirovich提出的称为快照(snapshot)[16]的方法。该方法可以将式(4)的高维矩阵求解特征值问题转化为一个与快照个数N相等的特征值问题。若一个样本包含M个数据,则取N个样本组成一个样本集U={U1, U2, …, UN}这是一个M×N阶的矩阵。该方法提出特征基函数可以由快照的线性组合构成,即
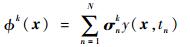
|
(5) |
其中:σnk为特征向量。将式(5)代入式(4)中可得到一个新的特征值问题:

|
(6) |
其中:λn为特征值;A的元素定义如下:
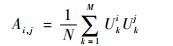
|
(7) |
其中特征值的大小可以表示该正交基函数在整个样本空间中所占能量的比重,即第s个最佳正交基方向上的物场理能量Es占总能量Etotal的比重εs为[4]

|
(8) |
式中:λs为第s个特征值。因此进行物理场的重建便可以根据能量的大小对基底进行选择。并不一定需要选择所有的基底来完成重建,假设M为所用正交基底的个数,有M≤N。一般M取得过大反而会受到舍入误差影响影响重建效果。在进行矩阵分解得到最佳正交基之后,对选取的正交基底与样本进行内积便可得到对应的系数向量:
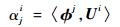
|
(9) |
本研究将POD理论用于翼型的二维冰形计算,主要考虑飞行迎角、飞行速度和结冰时间等多种物理参数对结冰冰形的影响。首先,利用不同状态下冰形轮廓点坐标值来构建样本矩阵;然后,利用前述的快照方法得到对应的快照矩阵A,对其进行矩阵特征分解得到对应的特征向量,也就得到了构建子空间的正交基及其系数向量。于是设计空间内的任意计算状态下的结冰冰形可以由这些正交基线性叠加表示为
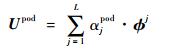
|
(10) |
式中:系数αjpod在一系列样本点状态下的值是已知的,即对应的重建系数αji,当需要计算其他非样本点状态时,系数αjpod获得则需要根据已有的系数αji利用插值模型进行插值。
1.3 Kriging模型假定已有N个快照的系数α定义了RK中N个超平面α(x)的值,其中K为自由参数的数目,x代表设计变量x=[x1, x2, …, xK]T,寻找α(x)的问题也就成为了超平面中的多维插值问题,在大多数的降阶模型应用中多采用多项式插值来决定系数,而在本研究中采用Kriging插值方法,Kriging插值方法可以接受任意数目的设计量,保证足够的插值精度而不会对计算时间造成影响,可以应用于任意维度的插值过程。
Kriging模型[17]是由南非工程师克里金(Krige)于20世纪50年代提出的, 现已广泛应用于各个领域,本文以普通克里金插值方法为例来说明克里金插值的原理[18]:
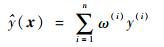
|
(11) |
只要得到了ω=[ω(1), ω(2), …, ω(n)]T的表达式,就可以得到参数空间中的任意设计点的估计值。Kriging模型的重要假设是将未知函数视为一个高斯随机过程, 该随机过程可以表示为

|
(12) |
式中:x为参数变量;F(β, x)称为全局趋势模型;H(x)为随机分布的误差。将随机过程的方差记为σ2,可用协方差描述不同位置点这些随机变量的相关性,其协方差可描述为
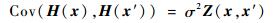
|
(13) |
其中:Z(x, x′)为相关函数(只与空间距离相关),相关性会随距离增大而不断减小。相关函数通常有指数函数、高斯函数、三次样条函数等多种形式。
基于上述假设,Kriging模型寻找最优加权系数ω,使得均方差最小,并且满足无偏差条件。
通常利用拉格朗日乘子法可以推导得出一个线性方程组,求解该方程组便可得到Kriging模型预估值为

|
(14) |
式中:Vkrig只与已有样本点相关;β0=(FTZ-1F)-1FTZ-1yk,yk为样本数据,F为一维单位向量,Z和z则是前述的相关函数矩阵及其中的相关向量,故便可利用样本数据得到模型的估计值。
构建Kriging模型时,还可以将对其模型参数(或超参数)也作为未知量来加入训练,可以进一步增强代理模型的灵活性。利用已有样本点和响应值可将问题转化为一个非线性无约束优化问题,一般采用“最大似然估计”或“交叉验证”得到超参数。对于最大似然估计而言,就是选择超参数使式(15)函数值达到最大[19]:

|
(15) |
式中:β0和σ2的最优值可以给出解析解为
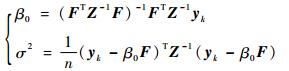
|
(16) |
将β0和σ2代入后,取对数忽略常数项,优化问题转化为
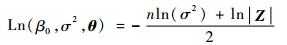
|
(17) |
利用数值优化算法如遗传算法、单纯形法、模式搜索法等训练超参数,就可以构建最终的Kriging模型。
2 冰形模拟及样本获取本文样本的获取依靠CFD的模拟获得,结冰的CFD模拟一般包括以下步骤:①空气流场计算;②过冷水滴或者冰晶、冻雨等流动情况求解及其撞击特性计算;③求解结冰热力学模型计算结冰量;④根据原有几何外形加上结冰量,完成冰形计算及几何形状重构。
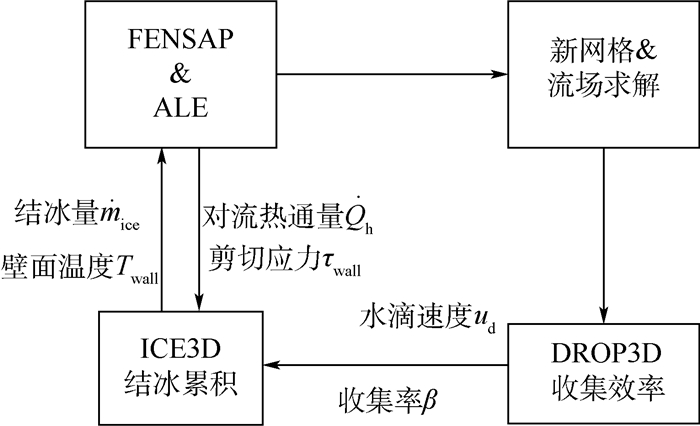
本文利用FENSAP-ICE软件[20]来进行结冰数值模拟,首先对基于雷诺平均的Navier-Stokes方程来求解得到空气流场,然后采用欧拉法计算模型表面的水滴撞击特性,最后求解结冰热力学模型计算结冰冰形。将结冰计算的步骤分为各个模块,其中FENSAP模块用于计算空气外流场,DROP3D模块用于计算水滴撞击特性,ICE3D用于热力学方程求解及冰形计算,模块相互关系如图 2所示。
|
| 图 2 FENSAP-ICE软件模块相互关系 Fig. 2 Relationship among FENSAP-ICE software modules |
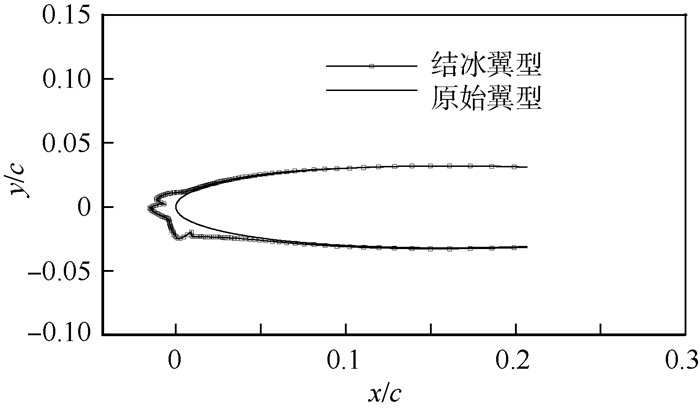
本文选用了NACA0012翼型为研究对象,根据相关文献选取了指定计算状态,用上述CFD方法先后调用各个模块进行结冰模拟,模拟结果得到的冰形如图 3所示。
|
| 图 3 FENSAP-ICE冰形模拟结果 Fig. 3 FENSAP-ICE ice shape simulation results |
从图 3中可以看出,冰形的轮廓点可以描述完整的冰形。因此可以取冰形上各个轮廓点的二维坐标值做为样本数据来进行后续计算。图 3翼型上表面网格点数为277,所以该算例一个样本包含277个数据。
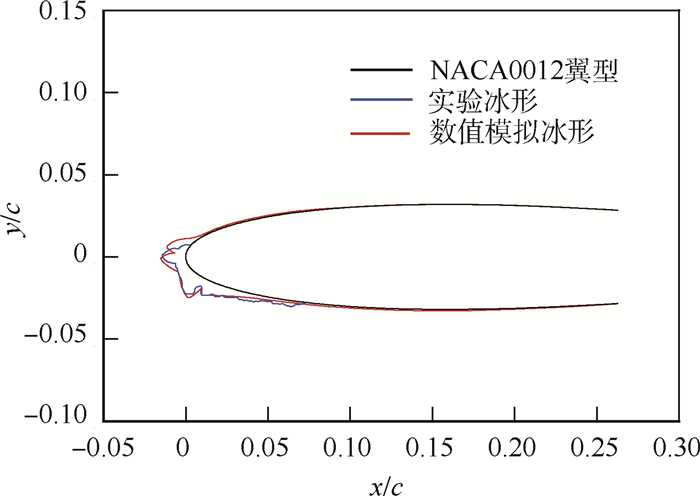
对于降阶模型的建立而言,样本数据的保真度对于模型的精度也是至关重要的,这里将上述模拟结果与实验数据进行了对比验证,对比结果如图 4所示,c为翼型弦长,表明了本文采用的数值模拟方法的可靠性。
|
| 图 4 冰形模拟与实验对比验证 Fig. 4 Comparison and validation of ice shape simulation and experiment |
本文先以单参数冰形预测为例,详细描述构建降阶模型的实施步骤。算例选择NACA0012二维翼型为研究对象,结冰冰形样本的获得是通过上述CFD方法来完成的。考虑飞行过程中的迎角变化对结冰冰形的影响来建立POD预测模型。选取的计算条件如表 1所示。
| 计算状态 | 数值 |
| 来流速度/(m·s-1) | 100 |
| 液态水含量(LWC)/(g·m-3) | 1 |
| 平均水滴直径(MVD)/μm | 20 |
| 环境压力/Pa | 101 325 |
| 结冰温度/K | 263.15 |
| 结冰时间/s | 360 |
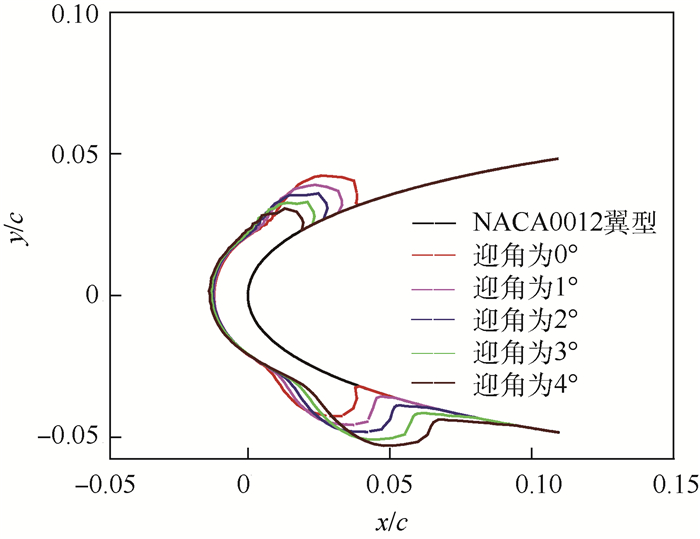
对于翼型而言,迎角的变化对气动性能有着重要的影响,同样它对结冰冰型也会产生很大的影响,分别选取了0°、1°、2°、3°和4°的结冰冰型作为样本集进行研究(样本个数为5),CFD模拟后得到的样本集冰形结果如图 5所示。
|
| 图 5 不同飞行迎角的冰形 Fig. 5 Ice shapes of different flying attack angles |
从图 5中可以看出,随着迎角的增加,翼型上表面的结冰范围越来越小,而下表面结冰范围越来越大。这是由于随着迎角的增大造成翼型下表面液滴撞击区域扩大,因此结冰范围向翼型下表面移动。本文对样本空间中的结冰冰形样本分别取出其冰形轮廓点的x、y坐标构成样本矩阵,样本矩阵的阶数为277×5。
利用数值模拟得到的样本矩阵采用快照方法进行简化得到对应的快照矩阵。这里一共选取了5个样本,故得到的快照矩阵为5×5阶。
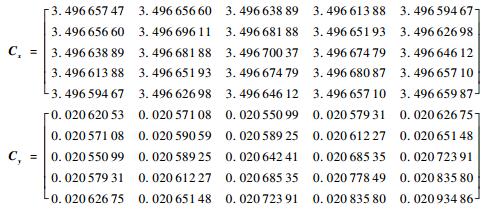
|
通过上面的x坐标快照矩阵可以看出,上述矩阵的元素差别很小,这是由于不同的冰形样本坐标大部分位置是相同的,只是在结冰位置略有差别,同时冰形的变化量相对于整个坐标来讲是小量,所以计算过程需要保证一定的数据精度。
在得到快照矩阵后,分别计算x、y的特征值λx、λy与特征向量(见表 2),可以看到第1个特征值明显大于其他,说明样本集的数据相似度很高。利用获得的特征向量便可以计算得到正交基,选取全部5个正交基进行POD冰形预测,可以得到每个样本在不同正交基上的系数如下表所示,可以看到第1个正交基明显系数大于其他,表明第1个正交基对POD计算结果的影响非常大。
| 特征值序号 | λx/10-6 | λy/10-6 |
| 1 | 174 832 6 | 10 328.48 |
| 2 | 8.937 12 | 20.761 14 |
| 3 | 3.189 29 | 5.440 25 |
| 4 | 1.121 569 | 1.452 005 |
| 5 | 0.613 951 | 0.556 798 |
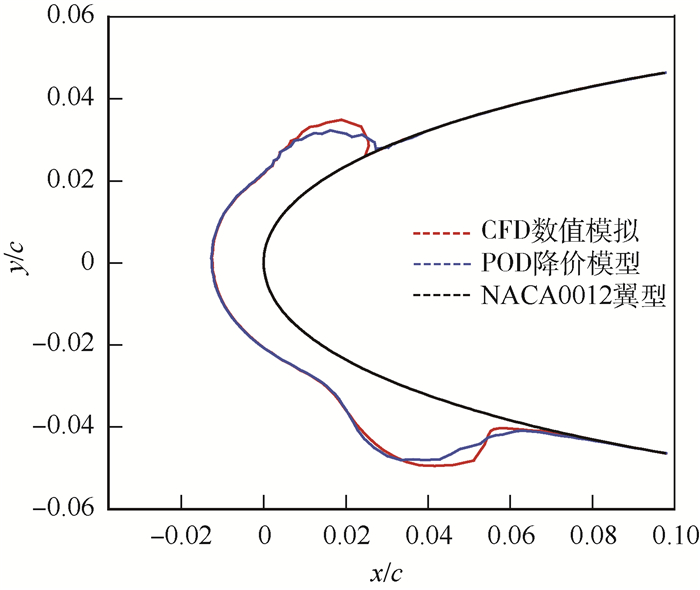
通过进行上述计算,基本建立了POD模型,这里利用前述的Kriging模型进行插值。选取迎角为2.5°的非样本点进行结果验证,最终的POD预测x、y坐标与CFD的计算结果对比如图 6所示,从图中可以看出POD的预测结果与CFD结果基本一致,只是在冰角以及结冰极限位置存在一些误差,说明POD预测方法是可行有效的。
|
| 图 6 单参数POD与CFD冰形对比 Fig. 6 Ice shape comparison between single-parameter POD and CFD |
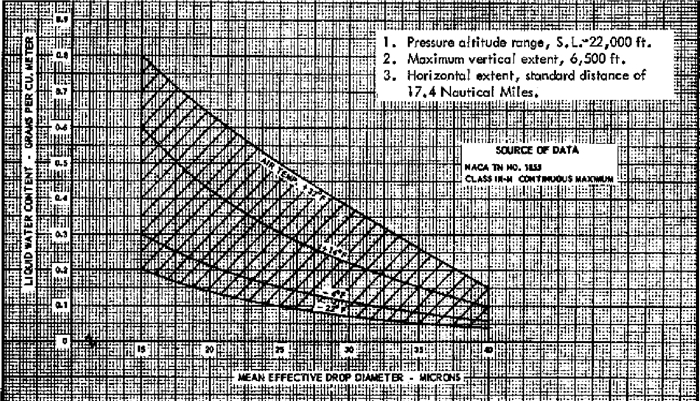
将POD方法扩展到多维情形,这里选取通常影响结冰的5个参数迎角、速度、温度、MVD、高度(选择范围如表 3所示, 1°F=-17.2℃, 1 ft=0.304 8 m)。结冰时间仍选择为360 s,另外LWC参数的选取考虑到实际的工程应用,按照连续最大结冰条件(见图 7)[21](FAR-25附录C)得到对应状态的液态水含量。
| 参数 | 最小值 | 最大值 |
| 飞行迎角/(°) | 0 | 5 |
| 飞行速度/(m·s-1) | 90 | 130 |
| 结冰温度/°F | -22 | +32 |
| MVD/μm | 15 | 40 |
| 高度/ft | 0 | 22 000 |
考虑到多参数样本选取的复杂性,为了保证一定的预测精度,本文选取了100个样本(见图 8),其样本空间的采样采用LHS方法。

|
| 图 8 样本空间分布 Fig. 8 Sample space distribution |
LHS方法是一种“充满空间的设计”,选取的样本点可以均匀地散布于参数空间。
与3.1节的单参数POD方法类似,多参数情形同样是利用上述样本空间的结冰冰型结果,可得到对应的100组样本二维坐标参数,然后通过POD方法得到对应的最佳正交基。由于多参数预测选取的样本数较大也会得到较多的正交基,这里只需要从中选取一些所占能量较大的正交基进行样本的重建即可。当选取的结冰冰形的预测正交基所占的能量总和如果大于99.9%,便可以认为它能完全反映样本冰形的主要特征[4]。然后再利用Kriging模型对重建系数进行插值,得到POD系数及最终的冰形预测结果。
利用上述的方法建立预测模型,选取的算例参数如表 4所示。
| 算例状态 | 数值 |
| 飞行迎角/(°) | 1.325 |
| 飞行速度/(m·s-1) | 91.875 |
| MVD/μm | 25.5 |
| 高度/ft | 12 031 |
| 结冰温度/°F | 16 |
| 结冰时间/s | 360 |
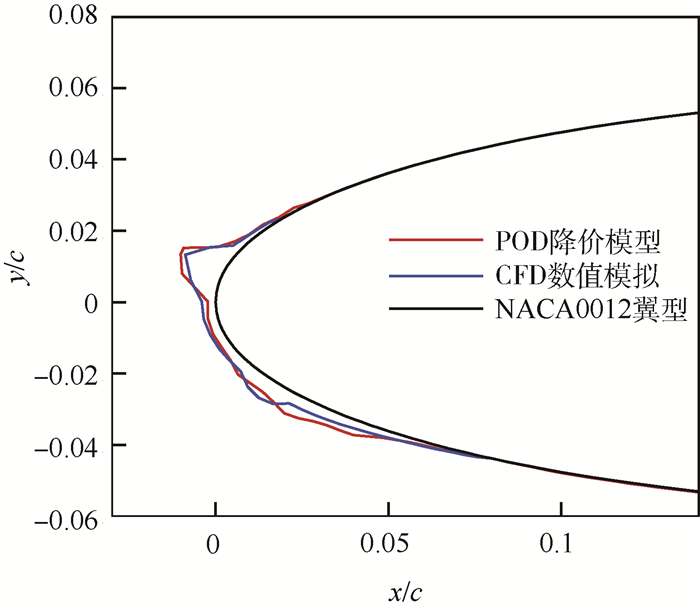
图 9为多参数的POD结果与CFD结果的比较,其中POD结果选取了能量总和占比达99.9%的最佳正交基计算得到,可以看出POD的预测结果与CFD结果吻合较好。
|
| 图 9 多参数POD与CFD冰形对比 Fig. 9 Ice shape comparison of multiparameter' POD and CFD |
传统Kriging模型采用确定的趋势模型,为了更好地改善近似精度, 文献[22]研究了一种利用贝叶斯框架来识别趋势模型的改进代理模型方法,称为“Blind-Kriging”模型。该模型的趋势模型不是确定的已知函数而是通过数据分析方法获得,具体理论为
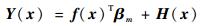
|
(18) |
式中:f(x)T=(1, v1, v2, …, vm), βm=(β0, β1, …, βm)T,同时m是未知的,这里同样H(x)代表一个随机过程,其协方差为σm2Z,相关函数Z也与模型阶数m有关。则Blind-Kriging的预测模型与通常的Kriging类似为

|
(19) |
其中:Fm=(f(x1), f(x2),…, f(xn))T, βm=(FmTZ-1Fm)-1; z(x)为相关函数。
Blind-Kriging最重要的步骤是识别出未知函数fi,这是通过函数(变量)选择技术在简单函数构成的候选函数集中选择得到,然后就可以得到预测模型的第一部分f(x)Tβm。
构建Blind-Kriging模型可以被看作是1个两阶段的过程。在第1阶段,建立一个普通Kriging模型,即具有常数回归函数的Kriging模型,完成模型构建和超参数θ估计。在第2阶段扩展该初始Kriging模型的回归函数,根据估计的α系数选择新的特征,生成一系列中间Kriging模型。当交叉验证错误满足要求时,中间Kriging停止迭代,然后选择最佳的特征组来构建最终Blind-Kriging模型,重新估计超参数θ。
比利时根特大学的研究人员已经开发了OODACE工具箱可以实现Blind-Kriging模型构建,本文的工作也是基于此工具箱开展的,其工具箱伪代码[23]如下。
X←samples
b1, …, bt{Candidate features}
b=Cte{Selected features}
θ0=maxθlikelihood(X, θ, b)
M0=construct(X, θ, b){Construct ordinary Kriging model}
α0=evaluateMeasure(M0){Assess accuracy}
i=0
while improvement(α){Accuracy improves?}
i=i+1
β=rank(b1, …, bt)
j=maxj(|βj|)
b=b∪bj
θi=maxθlikelihood(X, θ, b){Optional}
Mi=update(Mi-1, θi, b){Intermediate Kriging model}
αi=evaluateMeasure(Mi){Assess accuracy}
endwhile
θfinal=maxθlikelihood(X, θ)
Mfinal=update(Mi, θfinal, b){Final Blind Kriging model}
4.2 模型应用冰形预测仍选择为NACA0012翼型,考虑方法研究的目的,这里只选取参数为迎角与飞行速度,进行两参数的POD冰型预测,该方法同样可以扩展到多更多参数的应用中。分别选取了迎角为0°、1°、2°、3°和4°和飞行速度为90、100、110、120和130 m/s的结冰冰型作为样本集进行研究(M=25)。该算例选取的计算条件见表 5。
| 计算状态 | 数值 |
| MVD/μm | 20 |
| 环境压力/Pa | 101 325 |
| 结冰温度/K | 263.15 |
| 结冰时间/s | 360 |
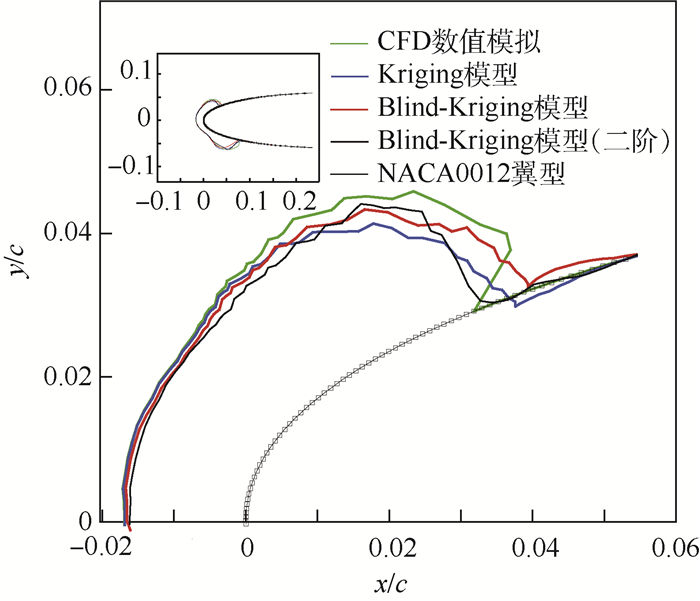
利用本文1.2节介绍的法进行了POD分析,并分别采用传统Kriging与Blind-Kriging模型进行预测。选取迎角为2.5°,飞行速度为115 m/s的非样本点进行模型对比,最终的POD预测与CFD的计算结果对比如图 10所示。从图中可以看出,POD的预测结果与CFD结果基本一致,不同插值模型的预测结果也比较类似,采用Blind-Kriging模型对于结冰冰型的粗糙度(非均匀性)预测未有很明显改善,为了改善预测精度,更好地发挥Blind-Kriging模型特点,选择在趋势模型中引入更高阶项,建立Blind-Kriging高阶模型可以发现对于冰型预测相比于低阶的Blind-Kriging模型预测结果精度有了较大改善,尤其对于结冰极限位置的预测相较于其他模型精度明显提高,表明了Blind-Kriging模型对于复杂冰型预测有着较好的适应性,尤其采用高阶模型能更好的发挥其先进性。
|
| 图 10 冰形预测结果对比 Fig. 10 Comparison of ice shape prediction results |
本文建立了一种基于POD和Kriging插值方法的降阶模型,利用CFD数值模拟的冰形结果作为样本来源,考虑了飞行迎角、飞行速度以及结冰温度的等多种物理参数对冰形影响,先后完成了单参数、两参数以及五参数情形下的翼型结冰冰形快速预测,得到:
1) 通过对POD预测结果与CFD结果进行对比可知:降阶模型可以得到较好的冰形预测效果,只是在冰角附近及结冰极限位置预测结果有细微的差别,表明该方法应用于翼型结冰冰形的预测是准确、可行的。
2) 利用贝叶斯框架下的Blind-Kriging模型进行数据插值虽然需要更多的时间完成模型建立,但可以改善降阶模型的精度,可以取得更为理想的冰形预测效果。
3) 虽然样本的取得需要一定的计算时间,但是降阶模型建立完成之后,便能够快速、准确地预测一定范围内任意状态的冰形。
4) 本文方法对涉及大参数研究的应用极具价值,如果预先计算足够的快照,则通过构建POD/Kriging逼近而不是使用全部的CFD解决方案来进行参数研究可以很容易节省大量时间。这为结冰试飞认证等工程应用提供了一种有效可行的方法,同时该方法可以推广应用至翼型设计阶段,对于容冰设计中的翼型结冰影响分析以及容冰优化设计是一种可靠准确的预测手段。
| [1] |
蒋天俊.结冰对飞机飞行性能影响的研究[D].南京: 南京航空航天大学, 2008. JIANG T J.Investigation of icing accretion influences on aircraft flight performance[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D052562 |
| [2] |
姚若鹏.翼型的结冰数值模拟及相关控制研究[D].南京: 南京航空航天大学, 2012. YAO R P.The numerical simulation of ice accretion on airfoil and control research[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D280454 |
| [3] |
杨胜华.二维飞机结冰过程仿真[D].北京: 北京航空航天大学, 2010. YANG S H.Two-dimensional in-flight ice accretion simulation[D].Beijing: Beihang University, 2010(in Chinese). |
| [4] |
申晓斌, 郁嘉, 林贵平, 等. 基于特征正交分解法的翼型结冰冰形快速预测[J]. 航空动力学报, 2013, 28(4): 807-812. SHEN X B, YU J, LIN G P, et al. Fast prediction of ice shape based on proper orthogonal decomposition method[J]. Journal of Aerospace Power, 2013, 28(4): 807-812. (in Chinese) |
| [5] |
GALLIVAN K, GRIMME E, VAN DOOREN P.Pade approximation of large-scale dynamics systems with lanczos methods[C]//Proceedings of the 33rd IEEE Conference on Decision and Control.Piscataway, NJ: IEEE Press, 1994: 443-448.
|
| [6] |
CAMUSSI R, GUJ G. Orthonormal wavelet decomposition of turbulent flows:Intermittency and coherent structures[J]. Journal of Fluid Mechanics, 1997, 348: 177-199. DOI:10.1017/S0022112097006551 |
| [7] |
AUBRY N, GUYONNET R, LIMA R. Spatio-temporal analysis of complex signals:Theory and applications[J]. Journal of Statistical Physics, 1981, 64(3-4): 683-739. |
| [8] |
HOLMES P, LUMLEY J L, BERKOOZ G. Turbulence, coherent structures, dynamical systems and symmetry[M]. Cambridge: Cambridge University Press, 1996: 68-100.
|
| [9] |
VOLKWEIN S.Proper orthogonal decomposition for nonlinear dynamical systems[EB/OL].Graz: University of Graz, 2005[2018-08-14] http://www.math.unikonstanz.de/numerik/personen/volkwein/PhDSchools/Volkwein_Part1.pdf.
|
| [10] |
NAKAKITA K, HABASHI W G, NADARAJAH S. Toward real-time aero-icing simulation using reduced order models[J]. Journal of Aircraft, 2010, 47(1): 96-115. DOI:10.2514/1.44077 |
| [11] |
葛宜元. 试验设计方法与Design-Expert软件应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2015: 2-3. GE Y Y. Experimental design method and Design-Expert software application[M]. Harbin: Harbin Institute of Technology Press, 2015: 2-3. (in Chinese) |
| [12] |
MCKAY M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239-245. |
| [13] |
MORRIS M D, MITCHELL T J. Exploratory designs for computational experiments[J]. Journal of Statistical Planning and Inference, 1995, 43(3): 381-402. DOI:10.1016/0378-3758(94)00035-T |
| [14] |
丁鹏, 陶文诠. 建立低阶模型的POD方法[J]. 工程热物理学报, 2009, 30(6): 1019-1021. DING P, TAO W Q. Reduced order modeling with the proper orthogonal decomposition[J]. Journal of Engineering Thermo Physics, 2009, 30(6): 1019-1021. DOI:10.3321/j.issn:0253-231X.2009.06.032 (in Chinese) |
| [15] |
KERSCHEN G, GOLINVAL J, VAKAKIS A F, et al. The method of proper orthogonal de-composition for dynamical characterization and order reduction of mechanical sys-tems:An overview[J]. Nonlinear Dynamics, 2005, 41(1-3): 147-169. DOI:10.1007/s11071-005-2803-2 |
| [16] |
SIROVICH L. Turbulence and the dynamics of coherent structures.Ⅰ-Coherent structures.Ⅱ-Symmetries and transformations.Ⅲ-Dynamics and scaling[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/1987-45-03 |
| [17] |
KRIGE D G. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the Southern African Institute of Mining and Metallurgy, 1951, 52(6): 119-139. |
| [18] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| [19] |
HÉLOÏSE B, FRANÇOIS M, WAGDI G H. FENSAP-ICE's three-dimensional in-flight ice accretion module:ICE3D[J]. Journal of Aircraft, 2003, 40(2): 239-247. DOI:10.2514/2.3113 |
| [20] |
JEONG S, OBAYASHI S, YAMAMOTO K. Aerodynamic optimization design with kriging model[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2005, 48(161): 161-168. DOI:10.2322/tjsass.48.161 |
| [21] |
JECK R K.Icing Design Envelopes(14 CFR Parts 25 and 29, Appenddix C)Converted to a Distance-Based Format: DOT/FAA/AR-00/30[R].Washington, D.C.: FAA, 2002.
|
| [22] |
JOSEPH V R, HUNG Y, SUDJANTO A. Blind Kriging:A new method for developing metamodels[J]. Journal of Mechanical Design, 2008, 130(3): 350-353. |
| [23] |
COUCKUYT I, FORRESTER A, GORISSEN D, et al. Blind Kriging:Implementation and performance analysis[J]. Advances in Engineering Software, 2012, 49: 1-13. DOI:10.1016/j.advengsoft.2012.03.002 |