为发挥导弹的最大效能,对目标实施“手术刀式”精确打击,不仅需要导弹精确击中目标,还期望导弹以指定角度攻击目标[1-2],因此研究带落角约束的制导律具有很强的实际工程意义[3]。
目前,关于带落角约束制导律的设计方法有多种多样。基于比例导引的思想,文献[4]设计了一种新型带落角约束的偏置比例导引律,其偏置项是剩余时间和落角误差的函数。基于最优控制理论,文献[5]以零脱靶量和零落角误差为约束,运用Schwartz不等式求出了带落角约束最优制导律的封闭解。基于模型预测静态规划理论(MPSP),文献[6]对用于角度控制的控制量进行迭代更新,使满足落角约束条件。基于滑模控制理论,文献[7]基于反演滑模设计带落角约束的制导律,并设计扩张观测器对目标机动信息进行估计。
基于滑模控制理论设计制导律对外界干扰具有很强的鲁棒性[8],因此被广泛应用在制导律设计中。
文献[9]基于非奇异快速终端滑模函数设计了滑模面,选取快速幂次趋近律设计了二维平面内带落角约束的制导律。文献[10]提出了一种有限时间收敛的积分滑模面,同样选取快速幂次趋近律,设计了二维平面内攻击机动目标带落角约束的制导律,并对未知机动目标干扰上界进行自适应估计。但文献[9-10]只在二维平面内设计了制导律,没有考虑三维空间中各通道间的耦合关系,使得制导律设计的实用性降低。文献[11]提出了一种带落角约束的三维有限时间滑模制导律,设计过程中没有对制导系统模型作解耦处理,但该制导律只能用于攻击静止目标。文献[12]采用快速双幂次趋近律设计了三维前向滑模制导律,保证了系统能够快速收敛到滑模面,但该制导律没有考虑导弹的落角约束问题。并且上述文献研究的都是一阶滑模制导律,而二阶滑模制导律具有抑制抖振能力强,鲁棒性强的优点[13],因此基于二阶滑模变结构控制理论设计带落角约束的三维有限时间收敛制导律具有很强的工程应用价值。
本文首先建立了完备的三维制导系统模型,无需对模型进行解耦处理。然后选取非奇异快速终端滑模面设计了非奇异快速终端二阶滑模制导律,并设计了非齐次干扰观测器,对未知目标机动信息和视线角耦合项进行估计并补偿,设计的制导律避免了传统终端滑模制导律中的奇异问题。最后对所设计制导律的稳定性和有限时间收敛特性进行了严格的数学证明。
现对本文提出的制导律优势进行说明:①制导律设计过程中考虑了三维耦合项,无需对系统模型作解耦处理;②设计了非齐次干扰观测器估计目标机动和视线角耦合带来的总干扰,无需目标先验信息;③选取非奇异快速终端滑模面设计二阶滑模制导律,收敛速度快,并且能够有效抑制抖振现象;④提出的制导律可以在三维空间中带落角约束攻击机动目标,工程应用价值强。
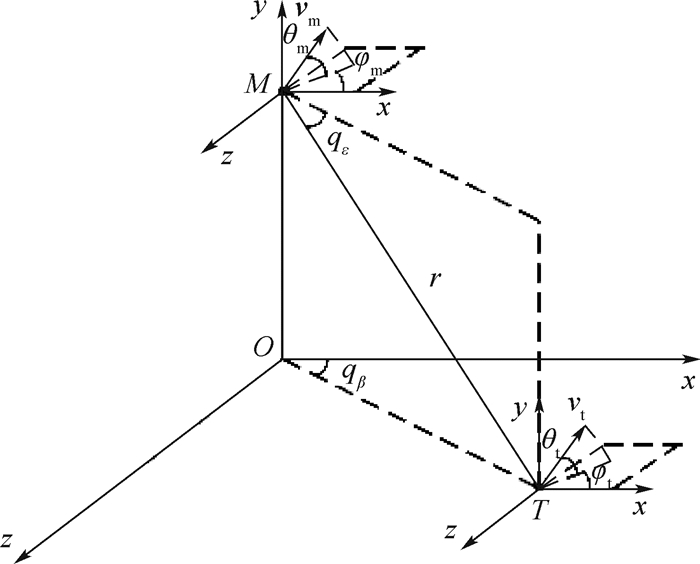
1 三维空间末制导系统模型考虑导弹在三维空间中攻击地面机动目标情形,导弹和目标的相对运动关系如图 1所示。
|
| 图 1 弹目相对运动关系 Fig. 1 Relative motion relationship between missile and target |
图 1中Oxyz为地面惯性坐标系,M和T分别为导弹和目标,r为弹目视线。qε和qβ分别为视线倾角和视线偏角,其方向定义为当r位于水平面Oxz上方时qε为正,当Ox轴逆时针旋转到r在Oxz面上的投影上时qβ为正。vm为导弹速度,θm和φm分别为弹道倾角和弹道偏角,其方向定义为当vm位于水平面Oxz上方时θm为正,当Ox轴逆时针旋转到vm在Oxz面上的投影上时φm为正。vt为目标速度, θt和φt分别为目标的俯仰方向航向角和水平方向航向角,其方向定义同导弹弹道倾角和弹道偏角方向定义。根据图 1得到三维空间下导弹-目标的相对运动方程为
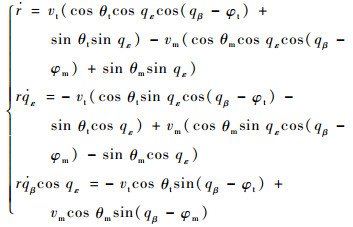
|
(1) |
导弹的动力学方程为

|
(2) |
式中:ax、ay和az分别为导弹加速度在速度方向、速度法向和速度侧向上的3个分量,大部分导弹在制导末段无推力作用,因此加速度是由作用在导弹上的合外力作用产生的。
将导弹速度vm在地面惯性坐标系Oxyz的3个坐标轴上分解得到三维空间导弹运动方程为
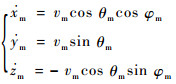
|
(3) |
同理将目标速度vt在地面惯性坐标系Oxyz的3个坐标轴上分解得到目标运动方程,这里不再赘述。
假设视线坐标系相对于地面惯性坐标系的旋转角速度为ω,其叉乘矩阵用[ω]×F表示。弹目相对速度、弹目相对加速度、导弹速度和导弹加速度在视线坐标系中的分量为vr、ar、vm和am,根据科里奥利定理,有如下关系成立:

|
(4) |
式中:
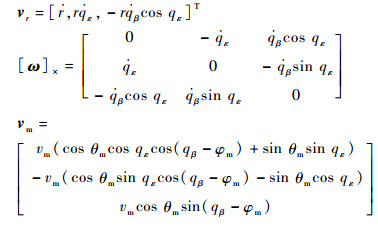
|
将式(4)第1式展开,得到
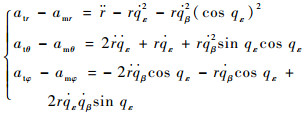
|
(5) |
式中:atr、atθ、atφ和amr、amθ、amφ分别为目标和导弹加速度在视线坐标系3个轴上的分量。
将式(4)第2式展开,并将式(2)代入化简得到ay、az与amθ、amφ的转换关系为

|
(6) |
在末制导段,弹目相对加速度在视线方向上的分量很小,对导弹脱靶量和落角误差的影响可以忽略不计,因此将导弹加速度在视线方向上的分量amr设定为0。为使弹道倾角和弹道偏角的变化率
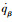
针对三维空间中导弹指定角度攻击地面机动目标问题,本节设计带落角约束的非奇异快速终端二阶滑模三维制导律。首先给出带落角约束的三维系统状态方程;然后选取非奇异快速终端滑模面设计了二阶滑模制导律,保证了系统快速收敛的同时有效抑制了抖振现象;最后针对系统中的目标机动信息和视线角耦合项设计了非齐次干扰观测器,用来对系统中的总扰动进行估计并补偿。
2.1 设计目标导弹击中目标时刻,导弹攻角可近似为0,根据文献[14],导弹攻击落角约束问题可以转化为视线角跟踪问题。
设导弹击中目标时刻期望的视线倾角和视线偏角分别为qεd和qβd,令x1=qε-qεd,x2=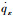
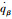

|
(7) |
式中:dθ和dφ分别为视线法向和视线侧向上目标机动信息和视线角耦合项带来的总扰动,其表达式分别为
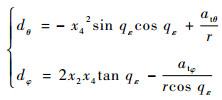
|
(8) |
本节设计制导律的目的是通过设计视线法向和视线侧向上的导弹加速度amθ和amφ,使系统方程式(7)在有限时间内收敛到0。并设计非齐次干扰观测器对系统中的总干扰dθ和dφ进行估计并补偿。
2.2 基于快速终端滑模面的二阶滑模制导律设计针对系统状态方程式(7),选取如下快速终端滑模面:

|
(9) |
式中:sig(x)ai=|x|aisgn(x), i=1, 2, 3, 4;k1、k2、k3和k4为大于0的正常数;1 < a2 < 2,1 < a4 < 2,且a1>a2,a3>a4。
对滑模面式(9)求导,并将式(7)代入得

|
(10) |
为使系统状态有限时间内收敛到滑模面,并沿着滑模面运动在有限时间内收敛到系统期望状态,针对式(10),本文设计制导律如下:

|
(11) |
式中:z1θ和z1φ分别为本文设计的非齐次干扰观测器对系统式(7)中总扰动dθ和dφ的估计值。设计参数α1、α2、β1和β2均为大于0的常数,且y>2,u>2。
本文提出的制导律式(11)中不含负指数项,因而避免了传统终端滑模制导律中存在的奇异问题。选取快速终端滑模面设计制导律,提高了系统收敛到期望值的速度。将制导律设计成二阶滑模制导律,并且制导律中不含非连续符号函数项,有效抑制了抖振现象。
对于系统式(10)中由视线角耦合项和目标机动信息带来的系统总扰动dθ和dφ,根据文献[15]中有限时间收敛的非齐次干扰观测器的定义,分别设计以下2种观测器对dθ和dφ进行估计。

|
(12) |
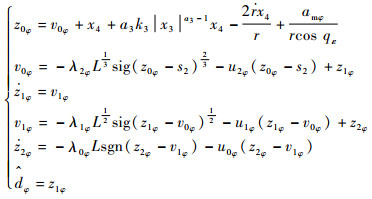
|
(13) |
式中:λiθ、λiφ、uiθ和uiφ均为大于0的常数;

当本文设计的非齐次干扰观测器稳定时,系统的稳定性和有限时间收敛证明分为两步,第1步证明系统状态在有限时间内到达滑模面,第2步证明系统状态沿着滑模面运动在有限时间内收敛到期望值。
证明 系统在有限时间内到达滑模面。
假设设计的非齐次干扰观测器式(12)和式(13)分别在时间tr1和tr2收敛到系统总干扰的真实值dθ和dφ,则当t≥max{tr1, tr2}时,将制导律式(11)对应代入到式(10),化简后得

|
(14) |
为方便分析,引入以下状态变量:

|
(15) |

|
(16) |
对式(16)求导得

|
(17) |
式中:矩阵A和B分别定义为
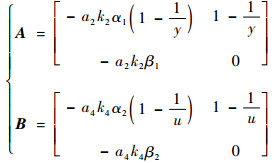
|
容易发现,矩阵A和B都为Hurwitz矩阵,因此对任意矩阵Q1=Q1T, Q2=Q2T, 存在对应矩阵P1=P1T>0和P2=P2T>0,满足如下代数黎卡提方程:
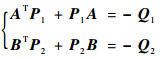
|
(18) |
对系统式(17)选取如下Lyapunov函数:
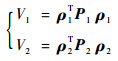
|
(19) |
对式(19)求导,可得

|
(20) |
将式(17)代入到式(20),得

|
(21) |
由式(16)可知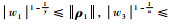
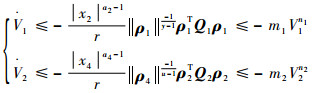
|
(22) |
式中:
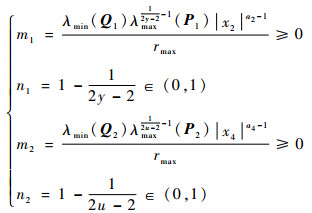
|
式中:λmin(·)和λmax(·)分别为矩阵(·)的最小特征值和最大特征值。根据式(22)可知,

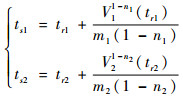
|
(23) |
式中:tr1和tr2分别为所设计的非齐次干扰观测器式(12)和式(13)收敛系统总干扰的真实值dθ和dφ的时间,式(23)表明系统状态将在有限时间内收敛到滑模面s1和s2。
当|x2|=|x4|=0,且max{tr1, tr2}≤t≤min{ts1, ts2}时,将制导律式(11)代入到系统式(7)中,可得

|
(24) |
因为系统状态未收敛到滑模面s1和s2,即s1≠0,s2≠0。此时
证明 系统状态在有限时间内收敛到期望值。
当t≥max{tr1, tr2},即系统状态收敛到滑模面s1=0, s2=0时,则式(9)变为

|
(25) |
对系统式(25),选取如下Lyapunov函数:

|
(26) |
对式(26)求导,并将式(25)代入可得
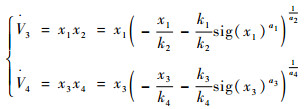
|
(27) |
将式(26)代入到式(27),化简后可得
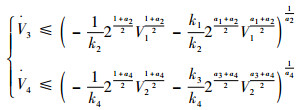
|
(28) |
观察式(28)可知,式(28)具有同式(22)的结构,同理由文献[16]中的引理1可得,x1和x3在有限时间内收敛到0。并且由式(25)可得,当x1=0,x3=0时,x2和x4也在有限时间内收敛到0。
证毕
4 仿真分析为了验证本文提出制导律的有效性和优越性,首先对不同位置不同状态的3枚导弹攻击同一机动目标进行仿真,验证本文制导律的优越性;然后在相同条件下与不同制导律进行仿真对比,验证本文制导律的优越性。
4.1 多枚导弹仿真分析为验证本文设计制导律的有效性和普遍性,考虑不同位置不同初始状态下的3枚导弹以各自指定角度攻击机动目标。假设目标的初始坐标为(10, 0, 10) km,速度vt=50 m/s,速度法向和速度侧向上的加速度分别为aty=1g(g为重力加速度),atz=0.5g,初始俯仰方向航向角和初始偏航方向航向角分别为θt0=10°, φt0=15°。3枚导弹速度恒定且均为600 m/s,导弹的初始导弹倾角和导弹偏角分别用θm0和φm0表示,期望视线倾角和视线偏角分别用qεd和qβd表示,3枚导弹的其余参数如表 1所示。
| 导弹 | 初始坐标/km | θm0/(°) | φm0/(°) | qεd/(°) | qβd/(°) |
| M1 | (0, 10, 0) | -25 | -20 | -30 | -30 |
| M2 | (2, 12, 1) | -10 | -30 | -60 | -20 |
| M3 | (-2, 9, 3) | 10 | 10 | -70 | -60 |
制导律式(11)中的参数设置如下:a1=a3=3,a2=a4=1.1,k1=k2=k3=k4=1,α1=α2=500,β1=β2=600,γ=2.1,u=2.1。观测器式(12)和式(13)参数取值如下:λ0j=1.1, λ1j=1.5, λ2j=2;u0j=3, u1j=6, u2j=8, j=θ, φ; L=0.1。制导盲区设置为20 m,即弹目距离小于20 m时导弹按进入制导盲区时刻加速度飞行,导弹过载限制为30g仿真步长设置为1 ms,仿真结果如图 2和表 2所示。

|
| 图 2 3枚导弹攻击目标仿真结果 Fig. 2 Simulation results of 3 missiles attacking targets |
| 导弹 | 脱靶量/m | 视线倾角误差/(°) | 视线偏角误差/(°) | 飞行时间/s |
| M1 | 0.206 9 | 0.011 6 | 0.025 7 | 29.768 0 |
| M2 | 0.077 6 | 0.010 0 | 0.025 0 | 29.979 0 |
| M3 | 0.296 2 | 0.029 3 | 0.015 9 | 30.362 0 |
从表 2和图 2(a)~(d)中可以看出,不同初始位置不同状态下的3枚导弹在制导律式(11)作用下均能够以指定视线倾角和视线偏角击中机动目标。3枚导弹的最大脱靶量不超过0.296 2 m,视线倾角和视线偏角误差控制在0.03°的范围内,验证了本文提出的制导律对脱靶量和落角误差的强控制能力。从图 2(e)、(f)中可以看出,视线倾角和视线偏角速率在有限时间内收敛到0,保证了导弹能够在有限时间内击中目标。从图 2(g)、(h)中看出,导弹的法向过载和侧向过载在制导末期均收敛到0附近,并且收敛过程中光滑平稳无抖振现象出现,保证了对导弹控制的稳定性。从图 2(i)、(j)中可以看出,滑模面s1和s2连续光滑地在有限时间连续内收敛到0,并且收敛过程中无抖振现象出现,验证了本文提出的制导律能够有效抑制抖振现象的出现。
4.2 不同制导律仿真对比为了进一步体现本文制导律的优越性,将本文提出的制导律记为SO-NFTSMG,与标准非奇异滑模制导律(记为NTSMG1)和文献[17]基于非奇异终端滑模面和快速幂次趋近律设计的一阶滑模制导律(记为NTSMG2)进行仿真对比。
现将2种制导律拓展到三维空间中,三维空间中NTSMG1的表达式为

|
(29) |
式中:K1和K2分别为符号函数增益,根据目标机动的上界选取,本文仿真中分别选取为50和100,式(29)中其余参数选取同制导律式(11)参数选取。
三维空间中NTSMG2的表达式为

|
(30) |
式中:参数选取同制导律式(11)参数选取。
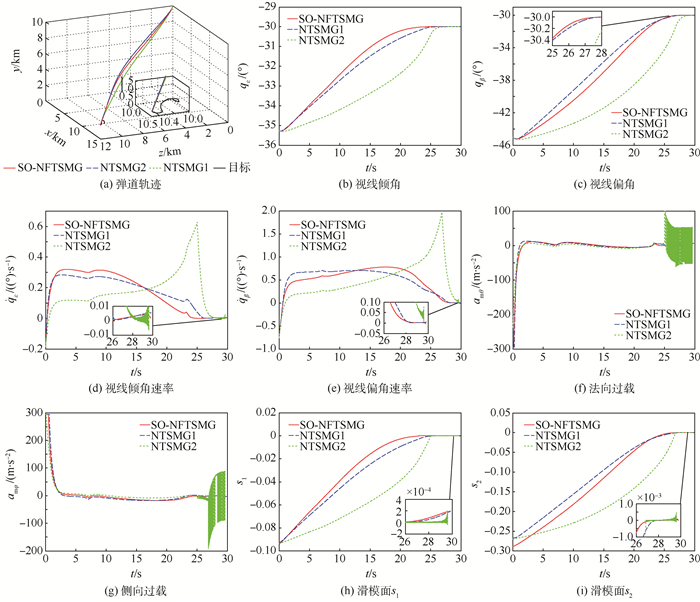
仿真选取4.1节中导弹M1分别在SO-NFTSMG、NTSMG1和NTSMG2的作用下攻击机动目标,目标初始值设置和制导律中参数选取同4.1节。仿真结果如图 3和表 3所示。
|
| 图 3 3种制导律仿真对比结果 Fig. 3 Simulation result comparison of 3 guidance laws |
| 制导律 | 脱靶量/m | 视线倾角误差/(°) | 视线偏角误差/(°) | 飞行时间/s |
| SO-NFTSMG | 0.206 9 | 0.011 6 | 0.025 7 | 29.768 0 |
| NTSMG1 | 0.268 1 | 0.023 6 | 0.026 1 | 29.706 0 |
| NTSMG2 | 0.242 3 | 0.011 4 | 0.027 3 | 29.923 0 |
从图 3中可以看出,3种制导律都能够控制导弹以指定角度击中机动目标。其中SO-NFTSMG收敛速度最快,并且收敛过程中光滑无抖振现象出现,验证了SO-NFTSMG良好的制导性能。NTSMG2收敛速度次之,并且由于NTSMG2中不含非连续符号函数项,收敛过程中抑制抖振现象明显。NTSMG1收敛速度最慢,并且收敛过程中出现了高频抖振现象,不利于导弹自动驾驶仪的控制。从表 3中可以看出,SO-NFTSMG作用下的导弹脱靶量最小,并且导弹飞行时间比NTSMG2短了约0.16 s,这对于飞行时间较短的导弹末制导段而言增大了突防概率。尽管NTSMG1作用下的导弹飞行时间最短,并且对脱靶量和落角的控制能力与SO-NFTSMG和NTSMG2相差不大,但由于NTSMG1的加速度指令出现了高频抖振,使得实际应用中对导弹的控制能力降低。实际应用中用饱和函数代替符号函数仍不能消除抖振现象,并且会造成制导律性能的下降。综合而言,本文提出的制导律SO-NFTSMG收敛速度最快,对脱靶量和落角的控制能力强,作用下的导弹飞行时间较NTSMG2作用下的导弹飞行时间短,并且制导指令中无抖振现象出现,利于导弹自动驾驶仪的控制。
5 结论本文基于非奇异快速终端滑模面和二阶滑模控制理论,提出了一种新型带落角约束的非奇异快速终端二阶滑模三维制导律。
1) 无需对系统模型作解耦处理,并且设计过程避免了奇异问题的出现。
2) 针对目标机动信息和视线角耦合带来的总扰动设计了非齐次干扰观测器进行估计,无需目标先验信息。
3) 通过2组实验仿真,结果表明:①本文提出的制导律能够控制不同位置不同状态下的多枚导弹以各自期望角度击中目标。②制导律对脱靶量和落角的控制能力强,飞行时间较NTSMG2缩短。③制导律收敛速度快,收敛过程中光滑无抖振现象出现,验证了本文提出制导律的快速收敛和抑制抖振能力强的优点。
本文在制导律的设计过程中未考虑自动驾驶仪的动态特性,在考虑导弹自动驾驶仪动态特性下设计制导律仍值得进一步研究。
| [1] |
黄诘, 张友安, 刘永新. 一种有撞击角和视场角约束的运动目标的偏置比例导引算法[J]. 宇航学报, 2016, 37(2): 195-202. HUANG J, ZHANG Y A, LIU Y X. A biased proportional guidance algorithm for moving target with impact angle and field-of-view constraints[J]. Journal of Astronautics, 2016, 37(2): 195-202. DOI:10.3873/j.issn.1000-1328.2016.02.009 (in Chinese) |
| [2] |
ERER K S, TEKIN R. Impact time and angle control based on constrained optimal solutions[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(10): 1-7. |
| [3] |
TAUB I, SHIMA T. Intercept angle missile guidance under time varying acceleration bounds[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 686-699. DOI:10.2514/1.59139 |
| [4] |
LEE C H, KIM T H, TAHK M J. Interception angle control guidance using proportional navigation with error feedback[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1556-1561. DOI:10.2514/1.58454 |
| [5] |
WANG H, LIN D, CHENG Z, et al. Optimal guidance of extended trajectory shaping[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1259-1272. DOI:10.1016/j.cja.2014.03.022 |
| [6] |
王晓芳, 王紫扬, 林海. 一种同时具有攻击时间和攻击角度约束的协同制导律[J]. 弹道学报, 2017, 29(4): 1-8. WANG X F, WANG Z Y, LIN H. A cooperative guidance law with constraints of impact time and impact angle[J]. Journal of Ballistics, 2017, 29(4): 1-8. DOI:10.3969/j.issn.1004-499X.2017.04.001 (in Chinese) |
| [7] |
张小件, 刘明雍, 李洋. 基于反演滑模和扩张观测器的带角度约束制导律设计[J]. 系统工程与电子技术, 2017, 39(6): 1311-1316. ZHANG X J, LIU M Y, LI Y. Backstepping sliding mode control and extended state observer based guidance law design with angles[J]. Systems Engineering and Electronics, 2017, 39(6): 1311-1316. (in Chinese) |
| [8] |
WANG X, HONG Y.Finite-time consensus for multi-agent networks with second-order agent dynamics[C]//Proceedings of the IFAC World Congress.Laxenburg: IFCA, 2018: 15185-15190. https://www.sciencedirect.com/science/article/pii/S1474667016414333
|
| [9] |
熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快速终端滑模制导律[J]. 控制理论与应用, 2014, 31(3): 269-278. XIONG S F, WANG W H, WANG S. Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J]. Control Theory & Applications, 2014, 31(3): 269-278. (in Chinese) |
| [10] |
赵斌, 周军, 卢晓东, 等. 考虑终端角度约束的自适应积分滑模制导律[J]. 控制与决策, 2017, 32(11): 1966-1972. ZHAO B, ZHOU J, LU X D, et al. Adaptive integral sliding mode guidance law considering impact angel constraint[J]. Control and Decision, 2017, 32(11): 1966-1972. (in Chinese) |
| [11] |
赵曜, 李璞, 刘娟, 等. 带碰撞角约束的三维有限时间滑模制导律[J]. 北京航空航天大学学报, 2018, 44(2): 273-279. ZHAO Y, LI P, LIU J, et al. Finite-time sliding mode control based 3D guidance law with impact angle constraints[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 273-279. (in Chinese) |
| [12] |
司玉洁, 宋申民. 拦截高超声速飞行器的三维有限时间制导律设计[J]. 中国惯性技术学报, 2017, 25(3): 405-414. SI Y J, SONG S M. Design of three-dimensional finite-time guidance law for intercepting hypersonic vehicle[J]. Journal of Chinese Inertial Technology, 2017, 25(3): 405-414. (in Chinese) |
| [13] |
ARIE L. Principles of 2-sliding mode design[J]. Automatica, 2007, 43(4): 576-586. DOI:10.1016/j.automatica.2006.10.008 |
| [14] |
SUN L H, WANG W H, YI R, et al. A noval guidance law using fast terminal sliding mode control with impact angle constraints[J]. ISA Transactions, 2016, 64: 12-23. DOI:10.1016/j.isatra.2016.05.004 |
| [15] |
LI P, PENG X F, MA J J, et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Proceedings of Chinese Automation Congress.Piscataway, NJ: IEEE Press, 2013: 120-125.
|
| [16] |
BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766. DOI:10.1137/S0363012997321358 |
| [17] |
周慧波.基于有限时间和滑模理论的导引律及多导弹协同制导研究[D].哈尔滨: 哈尔滨工业大学, 2015: 41-44. ZHOU H B.Study on guidance law and cooperative guidance for multi-missiles based on finite-time and sliding mode theory[D].Harbin: Harbin Institute of Technology, 2015: 41-44(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957301.htm |



