随着空间领域的研究、开发以及应用的不断提高,航天器功能与结构日趋复杂,航天器在轨服务技术可以有效地保证航天器在复杂的空间环境中持久、稳定、高质量地在轨运行,因而成为当前空间技术研究的热门[1-6]。航天器在轨服务技术主要包含在轨检查、交会对接和编队飞行等,其中涉及的一个核心问题是航天器的绕飞问题,即通过对任务航天器施加脉冲或推力,使其绕目标航天器作近距离周期运动。根据任务航天器绕目标航天器运动的周期与目标航天器本身运动的周期的比值,可以将绕飞分为“快速绕飞”与“慢速绕飞”。从更广的意义上说,通过对任务航天器施加脉冲或推力,使其与目标航天器距离始终保持在一定范围内,也可以称作绕飞。
作为经典相对运动方程,C-W(Clohessy-Wiltshire)方程得到了广泛的关注与应用。赵书阁和张景瑞[7]基于C-W方程研究了航天器共面圆型快速绕飞问题并相应分析了2种典型方法;林来兴[8]研究了绕飞轨道动力学和稳定性;师鹏等[9]基于线性动力学模型,分析了有限推力下的航天器绕飞性质;潘屹[10]对C-W方程的状态转移矩阵进行了推导,给出了选择悬停轨道的方法。这些理论进一步完善和发展了C-W方程理论,但工程应用价值有待提高。为了实现任务航天器对目标航天器的悬停或绕飞,设计基于脉冲控制和小推力控制的绕飞构型策略成为热门研究。Straight等[11]提出了以圆形轨道参考卫星为中心的特定环形区域内的特定点的脉冲制导方案;Hope和Trask[12]提出一种脉冲控制下的水滴悬停构型;Lovell和Tollefson[13]进一步给出了水滴悬停构型的参数表示方法;饶殷睿等[14]基于相对轨道要素描述了水滴悬停构型;王功波等[15]在圆参考轨道和连续小推力条件下,推导了快速绕飞策略;罗建军等[16]分析了快速受控绕飞;朱小龙等[17]提出了一种参数延拓方法,实现了有限推力bang-bang控制下的绕飞轨迹优化问题;张冉等[18]推导了4种受迫绕飞构型的解析表达式和脉冲控制策略,完善了受迫绕飞构型设计理论。
上述方法均可实现悬停或受迫绕飞,但模型构建存在一定的局限性。大部分研究都是基于圆轨道假设,即参考轨道是圆轨道,无法有效地解决非圆参考轨道下的受迫绕飞问题;对于悬停构型,大多采用脉冲推力或连续小推力实现构型的保持,工程应用难度较大。针对上述情况,本文提出了多段常值推力控制实现水滴悬停构型的打靶方程,分析了近距离相对运动条件下两段常值推力控制的可行性,数值仿真显示分段常值小推力可以实现水滴悬停相对运动,与脉冲推力或连续小推力控制相比,更加符合工程实际。
1 水滴悬停构型水滴悬停构型是航天器悬停构型中一种典型构型[19],可同时满足悬停和高精度要求。将构型建立在质心非惯性坐标系中,如图 1所示。

|
| 图 1 水滴悬停构型三维示意图 Fig. 1 Schematic diagram of 3D teardrop hovering configuration |
原点O表示目标航天器,受控航天器初始位置为A1,依次经过点B11、C11、B12。当受控航天器到达点B12时给予确定的脉冲,使其沿着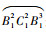

给出经典轨道摄动方程:
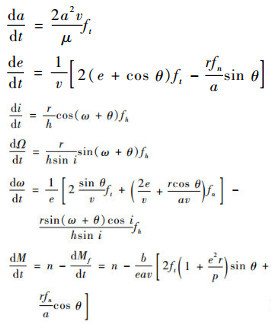
|
(1) |
式中:p、b、v、r和h为中间变量,

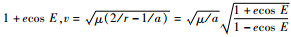
根据水滴悬停构型,可以得到施加脉冲前后任意时刻对应的轨道要素,不妨设施加脉冲前某时刻为t0,施加脉冲后的某时刻为tf,则对应的轨道要素分别为为X(t0)和X(tf),若在X(t0)处施加多段常值推力,使其在tf时刻轨道要素刚好为X(tf),则实现了用多段常值推力代替脉冲实现水滴悬停构型。
假定任务航天器在一个水滴周期内通过N段常值推力维持悬停构型,则常值小推力f可表示为

|
(2) |
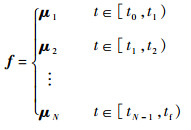
|
根据上述分析,可建立相应的打靶方程。

|
(3) |
因为摄动方程是高度非线性的微分方程组,无法直接求解常值推力解析解,同时每段推力的作用时间也未知,也是待求量,所以将原方程问题转化为极值问题求解,考虑到构造极值问题:
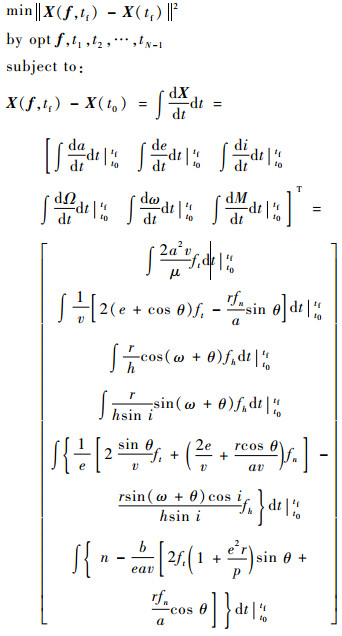
|
(4) |
显然,优变量随着推力段数的增加而增加,相应的计算时间也会大量增加,计算精度不能得到保证,且推力段数过多导致控制复杂,不利于工程实际应用。应当考虑采用尽可能少的推力段数实现常值推力控制。
2 单段常值推力与多段常值推力首先分析只采用一段常值推力下的情况:
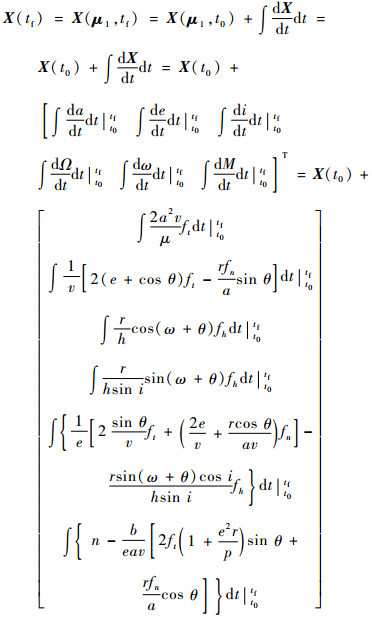
|
(5) |
式中:ft, fn, fh为t时刻μ1在3个方向上的投影分量。将μ1看作参数,根据常微分方程解对参数的连续依赖性,X(μ1, tf)为关于μ1的可微连续函数,即X(μ1, tf)局部上是一个三维微分流形,而X(μ1, tf)的值本身是六维空间的元素。显然,三维流形无法覆盖六维空间,也就是说,很多情况下,不存在满足条件的μ1,使得

|
(6) |
其次,考虑两段常值推力,假设两段常值推力作用时间相同,则代入最小二乘优化函数里,优化变量只有两段常值推力,即六维变量。小邻域定理保证了解的局部存在性。
小邻域定理:近距离运动假设下,固定时间内,对于参考轨道,存在一个小邻域对其中任意一点,一定存在两段常值推力解。
数学描述如下:
设




|
| 图 2 小邻域定理示意图 Fig. 2 Schematic diagram of small neighborhood theorem |
证明 根据小推力线化方程[20],有

|
(7) |
式中:E0、Eh和Ef为参考轨道X0(t)分别在t0、(t0+tf)/2和tf时的偏近点角;A(E0, Eh)与A(Eh, Ef)均表示线化矩阵,具体表示详见文献[20]在近距离运动假设下,小推力线化方程的系数矩阵C可以近似代替雅可比阵。det C≠0,所以雅可比阵行列式不为零,根据逆映射定理,一定存在一个小邻域满足一一映射。 证毕
根据小邻域定理,只要设计的推力曲线终端六要素位于以参考轨道终端时刻的六要素为圆心的小球内,常值推力一定有解,因此,若设计的推力曲线终端六要素与参考轨道终端时刻的六要素满足近距离相对运动假设,很大可能存在一对常值推力满足:

|
(8) |
其中:推力f满足:
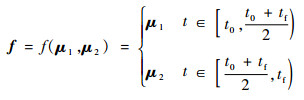
|
(9) |
采用最小二乘法得到的双段常值推力解往往精度较差,考虑采用迭代方法对解进行修正,提高精度准确性。
设映射函数
若存在根x0,使得F(x0)=0,且F(x0)的Jacobi矩阵JF(x0)满秩,若矩阵A≈JF(x0)。
则存在小领域δ,使得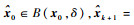
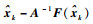
证明 对任意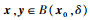
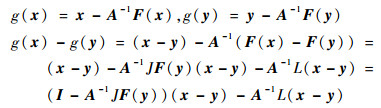
|
L为有界常数,仅与领域B(x0, δ)有关, 当x-y→0, L→0时,必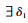
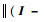
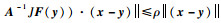
这是因为当x和y与x0接近,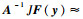
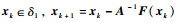
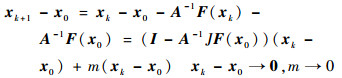
|
由公式:
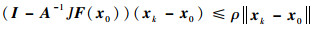
|
得

|
(10) |
故
故当x, y∈δ1时,g(x)是压缩的映射,由压缩映射定理,存在唯一不动点
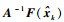
根据式(10),将最小二乘解当作初始点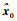

|
(11) |
可以提高最小二乘解的精度。
4 数值仿真设参考星K的轨道要素为X=(a, e, i, Ω, ω, M)=(7 555 000 m,0,π/4,0,0,0),其中半长轴单位为m。任务航天器W绕K作水滴悬停运动,水滴构型几何参数为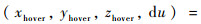
首先,根据方程式(4),采用最小二乘法尝试寻找一组多段推力解
|
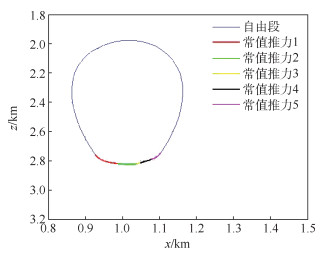
| 图 3 五段常值推力下仿真结果 Fig. 3 Simulation results of five-segment constant thrust |
在(x, z)=(930, 275 0) m时,任务航天器开始施加常值推力,直至(x, z)=(1 100, 2 750) m时停止施加推力,其中一共采用了5段常值推力,推力结束后,任务航天器进入自由段,不再施加推力,直到下一个周期/往复循环,表明确实存在多段常值推力控制可以代替脉冲推力使目标航天器绕参考星进行周期性水滴悬停运动,同时也说明最小二乘法可以较好地求解多段常值推力。
设参考星K的轨道要素仍然为X=(a, e, i, Ω, ω, M)=(7 555 000 m,0,π/4,0,0,0),半长轴单位为m,任务航天器W绕K作水滴悬停运动,水滴构型几何参数为
尽管5段常值推力实现了周期性水滴悬停运动,但计算时间较长,控制较复杂。为了减少求解时间,得到更简单的推力控制策略,考虑两段常值推力实现悬停构型,即在N=2的情况下进行了仿真,首先通过最小二乘法得到双推力初值,得到的结果精度差于5段常值推力控制,然后使用精度法对两段推力解进行精度修正,修正后的解精度较好,最后仿真结果如表 1和表 2所示。
| 推力/(m·s-2) | μ1 | μ2 |
| ft | 0.006 796 | -0.006 789 |
| fn | -0.018 311 | -0.018 306 8 |
| fh | 0 | 0 |
| 推力/(m·s-2) | μ1 | μ2 |
| ft | 0.005 074 | -0.005 080 |
| fn | -0.021 028 | -0.021 026 |
| fh | 0 | 0 |
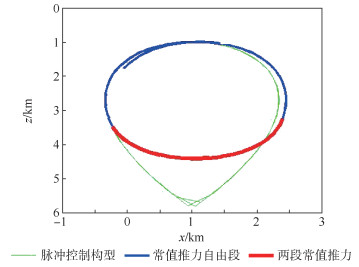
图 4为仅用最小二乘法得到的两段推力解。绿色轨迹代表施加脉冲推力的仿真效果,蓝色段表示为无推力段,红色段代表施加两段常值推力作用后的结果。可以看出,两段常值推力基本实现了水滴悬停构型控制,但控制精度较差,与原先构型重合度较差。
|
| 图 4 未修正的两段常值推力解 Fig. 4 Solution of unmodified two-segment constant thrust |
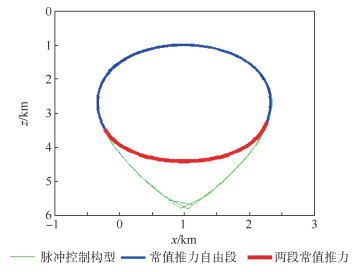
如图 5所示,绿色轨迹代表施加脉冲推力的仿真效果,蓝色段表示为无推力段,红色段代表施加两段常值推力作用后的结果。在(x, z)=(-300, 3 500) m时,任务航天器开始施加常值推力,直至(x, z)=(2 250, 3 300)m时停止施加推力,推力结束后,任务航天器进入自由段,不再施加推力,直到下一个周期往复循环。可以看到,红色段与绿色段重合度较高,说明双段常值推力解的精度较高,可以代替脉冲推力进行水滴悬停构型控制。
|
| 图 5 修正后的两段常值推力解 Fig. 5 Solution of modified two-segment constant thrust |
仿真结果表明,两段推力也可以很好地实现水滴悬停控制,具有较好的稳定性。由于待解变量较少,相比多段常值推力,计算速度更快。
5 结论基于脉冲控制下的水滴悬停构型和摄动方程,进一步研究可以得到:
1) 多段常值推力控制问题可以转化为求解水滴悬停构型的打靶方程,最小二乘法是一种求解此类问题的实用方法。
2) 小邻域定理为近距离相对运动条件下两段常值推力控制提供了可行性,悬停构型采用两段常值推力,一定程度上保证了解的存在性,也缩小了优化变量的数量,提高优化精度并减少优化时间。
3) 若最小二乘解的精度不够,但距离理想解不太远,那么采用迭代方法对最小二乘解进行修正,可以提高精度,甚至收敛到理想解。
| [1] |
张玉锟.卫星编队飞行的动力学与控制技术研究[D].长沙: 国防科技大学, 2002. ZHANG Y K.Research on dynamics and control technology of satellite formation flying[D].Changsha: National University of Defense Technology, 2002(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-2003097665.htm |
| [2] |
崔乃刚, 王平, 郭继峰, 等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805-811. CUI N G, WANG P, GUO J F, et al. A review of on-orbit servicing[J]. Journal of Astronautics, 2007, 28(4): 805-811. DOI:10.3321/j.issn:1000-1328.2007.04.005 (in Chinese) |
| [3] |
张雅声, 程文华. "女娲"计划:面向地球静止轨道的在轨服务系统[J]. 装备学院学报, 2017, 28(2): 40-45. ZHANG Y S, CHENG W H. Nu Wa project:On-orbit-service system for GEO[J]. Journal of Equipment Academy, 2017, 28(2): 40-45. DOI:10.3783/j.issn.2095-3828.2017.02.009 (in Chinese) |
| [4] |
汪新亮.在轨服务飞行器转移轨道设计及制导方法研究[D].长沙: 国防科技大学, 2014. WANG X L.Study on transfer orbit optimization and guidance methods of on-orbit service vehicle[D].Changsha: National University of Defense Technology, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1016921219.htm |
| [5] |
陈小前, 袁建平, 兆雯, 等. 航天器在轨服务技术(精)[M]. 北京: 中国宇航出版社, 2009. CHEN X Q, YUAN J P, ZHAO W, et al. Spacecraft on-orbit service technology[M]. Beijing: China Aerospace Press, 2009. (in Chinese) |
| [6] |
梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1): 1-13. LIANG B, XU W F, LI C, et al. The status and prospect of orbital servicing in the geostationary orbit[J]. Journal of Astronautics, 2010, 31(1): 1-13. DOI:10.3873/j.issn.1000-1328.2010.01.001 (in Chinese) |
| [7] |
赵书阁, 张景瑞. 航天器共面圆型快速绕飞控制研究[J]. 航天控制, 2014, 32(1): 68-72. ZHAO S G, ZHANG J R. Study on spacecraft coplanar circular fast flight control[J]. Aerospace Control, 2014, 32(1): 68-72. DOI:10.3969/j.issn.1006-3242.2014.01.013 (in Chinese) |
| [8] |
林来兴. 小卫星围绕空间站飞行动力学和控制研究[J]. 中国空间科学技术, 1999, 19(6): 1-6. LIN L X. A study on dynamics and control of small satellite flying around Space station[J]. Chinese Space Science and Technology, 1999, 19(6): 1-6. (in Chinese) |
| [9] |
师鹏, 李保军, 赵育善. 有限推力下的航天器绕飞轨道保持与控制[J]. 北京航空航天大学学报, 2007, 33(7): 757-760. SHI P, LI B J, ZHAO Y S. Orbital maintenance and control of spacecraft fly-around with finite-thrust[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(7): 757-760. DOI:10.3969/j.issn.1001-5965.2007.07.002 (in Chinese) |
| [10] |
潘屹. 航天器相对运动水滴型悬停轨道研究[J]. 航天器工程, 2014, 23(4): 13-18. PAN Y. Study on spacecraft relative drip-drop hovering orbit[J]. Spacecraft Engineering, 2014, 23(4): 13-18. DOI:10.3969/j.issn.1673-8748.2014.04.003 (in Chinese) |
| [11] |
STRAIGHT S D, TRAGESSER S G, HOWARD R, et al.Maneuver design for fast satellite circumnavigation[C]//AAS/AIAA 14th Space Flight Mechanics Meeting, 2004.
|
| [12] |
HOPE A S, TRASK A J.Pulsed-thrust method for hover formation flying[C]//Proceedings of AAS/AIAA Astrodynamics Specialists Conference.San Diego, CA: Univelt.Inc., 2008: 1-11.
|
| [13] |
LOVELL T A, TOLLEFSON M V. Calculation of impulsive hovering trajectories via relative orbit elements[J]. Advances in the Astronautical Sciences, 2006, 123(3): 2533-2548. |
| [14] |
RAO Y R, YIN J F, HAN C. Hovering formation design and control based on relative orbit elements[J]. Journal of Guidance, Control, and Dynamics, 2015, 152(2): 1-12. |
| [15] |
王功波, 孟云鹤, 郑伟, 等. 快速绕飞卫星空间圆编队设计方法[J]. 宇航学报, 2010, 31(11): 2465-2470. WANG G B, MENG Y H, ZHENG W, et al. Space round formation design method for fast flying satellites[J]. Journal of Astronautics, 2010, 31(11): 2465-2470. DOI:10.3873/j.issn.1000-1328.2010.11.005 (in Chinese) |
| [16] |
罗建军, 杨宇和, 袁建平. 共面快速受控绕飞轨迹设计与控制[J]. 宇航学报, 2006, 27(6): 1389-1392. LUO J J, YANG Y H, YUAN J P. Trajectory design and control for fast coplanar controlled flying[J]. Journal of Astronautics, 2006, 27(6): 1389-1392. DOI:10.3321/j.issn:1000-1328.2006.06.054 (in Chinese) |
| [17] |
朱小龙, 刘迎春, 高扬. 航天器最优受控绕飞轨迹推力幅值延拓设计方法[J]. 力学学报, 2014, 46(5): 756-769. ZHU X L, LIU Y C, GAO Y. Thrust-amplitude continuation design approach for solving[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 756-769. (in Chinese) |
| [18] |
张冉, 殷建丰, 韩潮. 航天器受迫绕飞构型设计与控制[J]. 北京航空航天大学学报, 2017, 43(10): 2030-2039. ZHANG R, YIN J F, HAN C. Spacecraft forced fly-around formation design and control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2030-2039. (in Chinese) |
| [19] |
饶殷睿, 韩潮, 殷建丰, 等. 航天器悬停构型设计与控制方法[J]. 航空学报, 2015, 36(7): 2361-2371. RAO Y R, HAN C, YIN J F, et al. Method of spacecraft hovering formation design and control[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2361-2371. (in Chinese) |
| [20] |
李鉴.连续推力轨道机动优化方法研究[D].北京: 北京航空航天大学, 2013. LI J.Research on continuous thrust orbit maneuver optimization method[D].Beijing: Beihang University, 2013(in Chinese). |



