无人机在多种应用领域发展迅速,如农林防护、遥感勘测、搜救救援、物流传送、武器装载等。从民用领域到军用领域,无人直升机越来越受到重视。其中小型无人直升机,拥有高操纵灵活性,可完成高难度特技飞行动作,应用前景广泛,潜力巨大。近些年,电器元件得到了进一步的优化,如传感器的尺寸大大减小,精度得到提升,控制芯片尺寸更加紧凑,可靠性更高。得益于电器元件的升级,小型无人直升机也相继改善,结构更加紧凑,载荷余度更大,机械结构得到优化。例如,对比以前的模型直升机,现在的模型直升机在机械结构上有一点不同,就是利用三轴陀螺仪来取代以前旋翼头上的伺服小翼稳定杆。没有了小翼结构以后,旋翼头的结构变得非常简单,减轻了维护和调试的难度。模型直升机具有高操纵性能,被很多研究机构应用到学术领域,用于探究小型无人直升机的飞行动力学特性及研究实现高级控制算法。当引入三轴陀螺仪以后,没有了伺服小翼在主旋翼之上旋转,主旋翼的入流将没有干扰,研究得到的动力学特性将更能反映主旋翼的特征。并且模型直升机利用三轴陀螺仪增稳,可以达到更高水平的操纵效果,操纵灵活性增加,飞行效果得到改善。陀螺仪就像一个黑箱模型,其内部控制模型是未知的,由于直升机基底模型过于灵活,为了飞行安全,在初始阶段陀螺仪不能被拆去,需要进行特别的研究处理。
首先看一下以往的小型无人直升机领域的研究经验,很多大学与研究组织将研究对象定位于成熟的直升机飞行平台上。将主要的飞行平台按质量从高到低列举:10~100 kg,Yamaha R-50[1]和AF25B[2];5~10 kg,MIT X-cell[3-5]、Evolution-EX[6]和NUS Raptor 90 SE HeLion[7];1~5 kg,Raptor 50[8];以及微型直升机领域:1 kg,HoneyBee[9]。虽然这些直升机平台的动力学特性各有差异,但是对于其动力学研究却有些共同点:
1) 总是希望获得简单却又精确的动力学模型。为了获得这个精确的动力学模型,最先可以想到的就是通过首要物理原则进行非线性建模。但是小型无人直升机由于低雷诺数的特点,详细的非线性建模无法保证在全部飞行包线内获得准确的估计。而且小型无人直升机不如全尺寸直升机数据丰富[10],建模具有挑战性。因此获取简单而局部精确的线性模型通常是较好的解决办法。多数研究获得的模型阶次不大于13阶[3],其中包含刚体机体动力学、旋翼挥舞动力学和稳定杆动力学等。以往的研究对于携带伺服小翼的机械增稳结构进行了动力学探讨,但是研究没有涉及携带三轴陀螺仪的控制增稳模型。
2) 总是通过借助实验数据来提取该飞行状态下精确的模型。在这个过程中,系统辨识方法占据重要的地位。系统辨识分为频域辨识方法和时域辨识方法。时域辨识方法有最大似然估计和子空间方法等,这些方法在不同的领域各有优点,如子空间方法在处理多输入多输出问题上具有优势[11-12],而最大似然法[13]应用于非线性数学模型(Nonlinear Mathematical Model,NMM)有优势。频域辨识方法则通过对比拟合飞行数据在频域上的信息来获取最优的模型。在频域领域测量噪声和过程噪声是没有估计误差的[14],这让闭环辨识问题变得简单,而且频域信息的分析更能帮助如鲁棒控制方法的设计[15-16]。CIFER软件是公认的具有高可靠性的频域辨识工具[1, 2, 14, 17]。
当简单的线性模型不能满足研究的需求时,为了改善模型精度,可以通过增加模型的阶次来反映更多的高频信息。文献[8]提出了一种12自由度的模型结构(包含桨叶锥度角和入流状态变量),与6自由度模型相比,12自由度模型有更高的精确度,但飞行数据的相干值参数较低,尤其在高频范围,这样会降低高阶模型辨识的可靠性。文献[18]将注意力放在挥舞动力学上,增加6个状态参数去表示挥舞角,此做法是为了提高模型在高频领域的表达力。但是提高模型阶次的方法都有一个弊端,就是增加的变量无法被观测到,也就很容易偏离真实的物理数值。
在上文分析中,线性模型简单而局部精确,但却是对复杂的NMM做出的一种妥协,因为当着眼于更广阔的飞行状态,如前飞状态,线性模型的局部精确将无法满足要求。一些研究者尝试于借助非线性结构来获取高精度动力学模型。如文献[6]利用时域辨识方法获取一个小型无人直升机的NMM。通过解析搭建NMM,提取出10个未知变量进行辨识,最后得到了较好的时域仿真效果。相似的非线性辨识研究,如文献[2]提取出12个未知参数利用基因算法收敛求解最优值,该方法对比预测误差法提取的线性模型有更好的仿真精度。文献[19]搭建了一个30状态变量的非线性直升机模型,通过从该NMM中提取不同状态下的线性模型再进行系统辨识调试,然而该方法需要多种状态下的飞行数据作为对比输入才能实现。
基于以上的研究背景,为了处理携带三轴陀螺仪的小型无人直升机的动力学研究问题,采用以下方法:首先,携带三轴陀螺仪进行闭环系统辨识实验,同时采集陀螺仪之前控制信号及陀螺仪之后控制信号。然后,应用2种输入信号进行辨识,由于考虑到闭环特征,应用频域辨识方法,同时获取双系统线性模型;与此同时搭建NMM,提取出重要的非线性参数,应用线性辨识结果进行修正,而NMM的轴外耦合参数也可给予线性辨识过程进行参考;由于陀螺仪之后控制信号具有高频特性,考虑增加高阶模型结构来改善线性模型的仿真精度。最后,将线性模型与NMM的仿真结果同实验数据作对比,得出结论。
1 非线性飞行动力学建模如图 1所示,本文的研究对象是JR700直升机。该直升机为电动驱动,是单旋翼带尾桨结构,无小翼。一个三轴陀螺仪安装在机身上部,起到增稳作用。机上计算机悬挂在机身下部,记录飞行时的操纵手控制信号、陀螺仪输出控制信号和直升机的响应数据。为了飞行安全,2个安全杆被安装在起落架上,长为1.5 m,每个安全杆质量为180 g。表 1将JR700的结构参数同其他3种小型无人直升机进行对比,JR700质量为8.1 kg,与其在相同量级的是X-cell和HeLion,而Raptor50的质量只有JR700的一半。然后,进行非线性动力学建模,小型无人直升机动力学模型主要分3个部分:刚性机体动力学、旋翼动力学和尾桨动力学,下面进行详细介绍。

|
| 图 1 JR700直升机系统 Fig. 1 JR700 helicopter system |
1.1 刚性机体动力学
刚性机体动力学在全机动力学的低频领域占据主导地位。通过以下2种方法来获取机体非线性建模的重要参数。
1.1.1 直接测量法由于本文研究的小型无人直升机已经有精确建模的CATIA模型和实物直升机,通过直接测量法,可以直接获得一些重要的尺寸参数,如旋翼直径、旋翼位置、尾桨参数、操纵杆尺寸角度和桨距角等。
1.1.2 地面物理实验参数(如转动惯量和重心)需要通过设计额外的全机实验来获取。三轴转动惯量可以通过三线摆法来测得[20]。将机身以三轴方向悬挂,通过记录摆动时间,可以求出转动惯量。而全机重心的获取格外重要,因为机上计算机和传感器位置相距全机重心是有偏差的,所以测量的飞行数据中所有的线速度值都有臂杆效应的误差。这个误差可以通过精确测量重心位置来修正。小型无人直升机的结构有一个特点,就是左右对称,这就给测量重心提供了便利,只需找到侧面重心即可。通过在侧向平面进行悬线法对全机进行多线悬挂,并拍摄高质量图片,以刻度尺为参考,在CAD界面处理悬线的位置并获得交点,进而得到精确的重心位置。经过测试,重心位置的误差可以控制在1 mm以内。假设观察点为P,重心为O,则修正线速度满足:
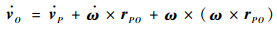
|
(1) |
式中:rPO为P到O的距离矢量;线性速度为v=[u v w]T,u为前向线速度,v为侧向线速度,w为垂向线速度;角速度为ω=[p q r]T,p为滚转角速率,q为俯仰角速率,r为偏航角速率)。
然后通过参数建模,确定各个部件的力与力矩。由牛顿欧拉方程组,可以推导出6自由度机体运动方程(机体坐标系的定义见文献[21]):
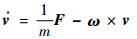
|
(2) |
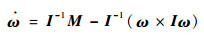
|
(3) |
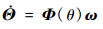
|
(4) |
式中:m为飞机质量;三轴欧拉角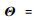
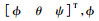
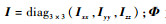
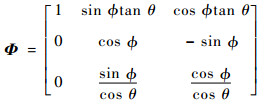
|
(5) |
对于小型无人直升机来说,机身和垂尾立板的受力可以适当简化计算[22-23],但是旋翼和尾桨动力学需要详细建模,这样可以让模型更能反映真实的气动特性。在本文中,主旋翼做均匀入流假设,旋翼拉力通过叶素理论来计算[24]。初始的桨叶气动参数,如升力系数、阻力系数和力矩系数由CFD方法来确定。
直升机的低频特性由刚性机体动力学表现,而直升机的高频特性则由旋翼来体现。通过分析频域数据,发现直升机的主轴响应p/δlat和q/δlon有二阶特性(δlat和δlon分别为横向和纵向周期变距,标准化为[-0.5, 0.5]之内)。其中一阶主要由刚性机体表示,另外一阶则反映旋翼的挥舞动力学。除了主轴方向的二阶特性,纵横向的耦合也十分明显。为了描述这些动力学特征,引入二阶稳定的一阶耦合桨尖轨迹运动方程[3]:
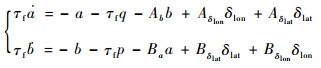
|
(6) |
式中:a和b分别为纵向和横向挥舞角;τf为旋翼时间常数;Aδlon、Aδlat、Bδlat和Bδlon为操纵系数;Ab和Ba为交叉耦合项:
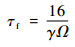
|
(7) |

|
(8) |
其中:Kβ为挥舞刚度;Iβ为挥舞惯性系数;Ω为旋翼转速;γ为桨叶洛克数。可以注意到,挥舞方程(式(6))已经是线性形式,这对接下来的模型修正十分便利。为了描述该小型无人直升机,以上的初始挥舞方程忽略了二阶挥舞项和锥度效应,保持了旋翼模型适当的复杂度,其有效性将在3.1节辨识分析中详细讨论。
1.3 尾桨动力学对于小型无人直升机来说,航向控制格外具有挑战性。在常规模型直升机上,一轴航向陀螺仪是必备的航向稳定部件。航向陀螺仪的作用是实时驱动尾桨桨距改变尾桨拉力来平衡主旋翼的扭矩,保证在无操纵情况下,直升机航向锁住一个方位不变,即锁尾功能。在JR700直升机上,安装的是三轴陀螺仪Futaba CGY750,包含一轴航向锁尾功能和两轴的纵横向增稳功能。在之前的辨识研究中,航向辨识获取航向模型的效果较差[8, 25],携带陀螺仪的尾桨动力学值得更深入探讨。与文献[3]相似,JR700的尾桨动力学在频域展现为二阶的总体特性。在文献[23]中,尾桨动力学由线性积分反馈(PI)环节来近似,得到了比较好的匹配效果,但是动力学在有反馈和无反馈的情况下没有进行良好的区分。文献[25]也只是在陀螺仪的基础之上增加额外控制律来改善小型无人直升机的航向性能,并没有进行深入研究。因此,本文提出三阶段辨识法来处理带陀螺仪的尾桨辨识问题。尾桨动力学结构如图 2所示。

|
| 图 2 尾桨动力学结构 Fig. 2 Tail rotor dynamics configuration |
阶段1 Gr_base:尾桨动力学基底模型。
阶段2 H1和H2:陀螺仪线性近似模型。
阶段3 Gr_all:尾桨动力学陀螺仪增稳模型。
根据线性化理论,尾桨动力学基底模型可以被看作是一阶系统:
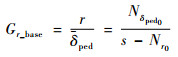
|
(9) |
式中:δped和δped为尾桨桨距控制量,标准化为[-0.5, 0.5];Nδped和Nr分别为航向力矩操纵导数和气动导数,下标0为了区分式(14)的结果。陀螺仪模型Gr_gyro由PI控制系统表示[23]:

|
(10) |
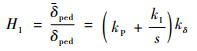
|
(11) |
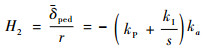
|
(12) |
式中:kP和kI的大小,可以通过地面的尾桨桨距阶跃输入,得到的响应数据确定;ka和kδ可由地面的航向扫频动作来确定。
通过Gr_base和Gr_gyro 2个模型,可以进而推导出外部增稳模型Gr_all:
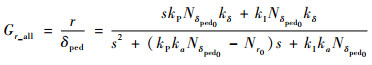
|
(13) |
为了使二阶模型线性化,引入新增变量rx到总体模型Gr_all之中:

|
(14) |
通过对比式(13)与式(14),可得

|
(15) |
在悬停和近悬停飞行中,航向通道与其他通道耦合程度很小,因此对航向通道进行单通道辨识。式(15)给出了从阶段1到阶段3求解Gr_all的方法。但实际上利用陀螺仪之前和陀螺仪之后的操纵数据作为辨识输入,Gr_all和Gr_base都可以通过单输入单输出(SISO)辨识获得线性模型。也就是说双系统辨识和三阶段辨识法推导可以相互修正与验证,来获取更真实的尾桨动力学模型。
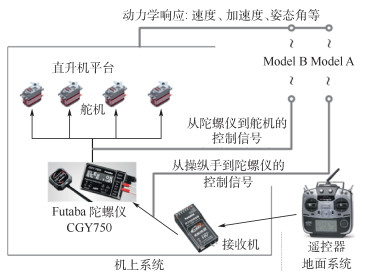
2 双系统线性模型辨识和模型修正方法 2.1 双系统线性模型辨识如图 3所示,Futaba CGY750三轴陀螺仪被安置在接收机和4个舵机之间。机载计算机负责同时记录控制信号和动力学响应数据。为了提取直升机在有无陀螺仪作用下的动力学模型,机载计算机同时记录从操纵手到陀螺仪的信号,及从陀螺仪到舵机的信号。通过利用这2组输入和输出的响应数据,进行系统辨识,可以获得辨识模型(Identification Model,IDM)。Model A代表包含陀螺仪的全机增稳模型,Model B代表不包含陀螺仪的基底模型。在本实验中,三轴陀螺仪Futaba CGY750的基本设置为:Flt.Mode=3,Pit.Rate=0.4,Ele.Rate=0.6,Ail.Rate=0.6。响应信号记录有:3轴线加速度ax、ay、az,三轴角速率p、q、r和三轴欧拉角θ、ϕ、ψ。
|
| 图 3 信号系统示意图 Fig. 3 Signal system illustration |
本文系统辨识过程是在频域领域完成的,借助于CIFER软件(由NASA Ames Research Center开发)。操纵手通过在俯仰、横滚、总距和航向通道分别执行扫频操纵,获取如图 3所示的Model A和Model B的输入输出数据,转换为频域信息并分别进行辨识。频域数据的相干值参数γxy2是决定系统频域特性的重要参数。对于小型无人直升机来说,操纵响应既包含低频成分也包含高频成分。JR700高质量高频信息大多包含在10~30 rad/s范围内。在本文的辨识过程中,为了保证频域数据的有效性,按频率截取30 rad/s以下,且按相干值参数截取0.6以上的。除此以外,有2个参数的辨识设置要格外说明:前向速度导数Xu和侧向速度导数Yv,这2个参数主要反映在低频领域,可独立辨识,传递函数可由机体运动方程得到:
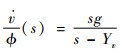
|
(16) |

|
(17) |
式中:g为重力加速度。因为参数Xu和Yv具有低频特性,所以辨识频域范围为[0.3, 4] rad/s。通过最小化价值函数Jave[14],使其低于100,Model A和Model B的未知参数可以在CIFER中辨识得到。软件中多输入多输出(MIMO)辨识利用到FRESPID、MISOSA、COMPOSITE和DERIVID模块,逐步得到结果。
2.2 非线性-线性模型结合修正方法通过第1节的建模,得到一个JR700小型无人直升机的11阶NMM。由于在NMM的建立过程中,有许多无法避免的假设与简化,导致NMM不会很精确,因此,应用一种非线性-线性模型结合修正方法来提高模型的精度。接下来详细介绍这种修正方法:
步骤1 通过实验数据获取线性模型IDM。
Model A和Model B状态变量分别为

|
(18) |
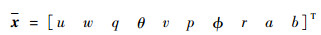
|
(19) |
注意到状态变量中不包含ψ,因为参数ψ决定特征值为0,其存在与否不影响直升机整体动力学特性,所以在这里略去[23]。
Model A状态空间模型为
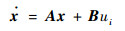
|
(20) |
式中:ui为操纵输入变量。

|
(21) |

|
(22) |
其观测变量为

|
(23) |
由于状态变量的不同,相对于Model A来说,Model B的状态矩阵A移去了第9行和第9列,而操纵矩阵B移去了第9行。对A、B矩阵的参数进行分类,以下几组参数为决定性参数,影响着主轴响应的精确度:纵横向耦合参数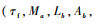
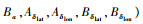
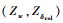
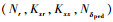
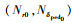
步骤2 利用IDM决定性参数修正NMM。
通过第1节可以发现,在NMM的建模过程中,挥舞模型和航向模型都是由线性模型表示的,所以在这2个方向NMM的参数可以很方便地由IDM参数修正。剩余的决定性参数需要详细的了解其解析意义。解释如下:
1) Zw和Zδcol
对于垂向方向来说,在整个飞行包线内主旋翼对于参数Zw和Zδcol都起到主要作用[21]。

|
(24) |

|
(25) |
式中:a0为桨叶升力线斜率;ρ为空气密度;R为桨叶半径;Kcol为桨距角的转化比例系数,使θcol(rad)→δcol([-0.5, 0.5])。
通过式(24)和式(25),可知通过辨识得到的IDM中Zw和Zδcol参数,可以修正NMM中的参数a0和Kcol,来提高垂向仿真的精确度。
2) Ma和Lb
与垂向动力学相似,纵横向耦合动力学同样由主旋翼主导。旋翼的纵向力矩Mmr和横向力矩Lmr可以由以式(26)和式(27)表示:
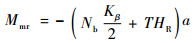
|
(26) |
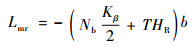
|
(27) |
式中:Kβ为挥舞刚度;Nb为桨叶个数;HR为旋翼距离重心的垂向距离;T为旋翼升力。则
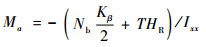
|
(28) |
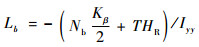
|
(29) |
因为I可以通过物理方法测量得到,而Ma和Lb可以由IDM获得。通过对比计算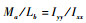
3) Xu和Yv
x方向的受力由2个部分组成:主旋翼受力和机体受力。
则x方向速度导数为

|
(30) |
式中:下标mr表示主旋翼, f表示机身。
修正总体的速度导数如下:
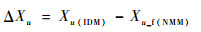
|
(31) |
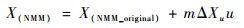
|
(32) |
式(31)、式(32)可以确保悬停附近时NMM有高的准确度,但是其前飞特性需要再次验证。
y方向受力由3方面决定,则速度导数为
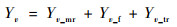
|
(33) |
式中:下标tr表示尾桨。
则NMM中y方向的修正公式为

|
(34) |
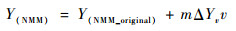
|
(35) |
步骤3 利用NMM的轴外耦合导数修正IDM。
对于IDM来说,除了决定性参数以外,还有6个参数需要决定:Mu、Mv、Lu、Lv、Xa和Yb。这6个参数由NMM初始决定。
总的来说,通过这3步,IDM和NMM达到相互修正的效果,最终获得更高精确度的悬停模型。
3 辨识结果分析与实验验证 3.1 模型结构验证与分析在进行全机模型辨识之前,首先要检查模型的结构是否合适。而主旋翼动力学比较复杂,模型结构需要多次修正来达到最好的整体辨识效果。表 2展示了Model A和Model B的耦合纵横向辨识模型结果,其中应用的挥舞模型见式(6)。
| 参数 | Model A | Model B | |||||
| 数值 | CR(Cramer-Rao)/% | 敏感度/% | 数值 | CR(Cramer-Rao)/% | 敏感度/% | ||
| τf | 0.078 41 | 10.01 | 0.895 9 | 0.055 95 | 8.32 | 1.066 | |
| Ma | 195.10 | 11.54 | 2.248 | 440.4 | 6.59 | 2.656 | |
| Lb | 224.12 | 20.05 | 2.010 | 740.2 | 5.765 | 2.521 | |
| Ba | 0.275 6 | 10.44 | 2.241 | 0.252 2 | 17.47 | 8.066 | |
| Ab | 0.275 6 | 0.252 2 | |||||
| Aδlat | 0.034 64 | 11.88 | 2.444 | 0.083 12 | 9.017 | 2.165 | |
| Aδlon | 0.386 3 | 8.710 | 1.693 | 0.446 2 | 8.122 | 1.962 | |
| Bδlat | 0.407 4 | 9.563 | 1.538 | 0.508 9 | 7.983 | 1.859 | |
| Bδlon | -0.042 43 | 14.75 | 3.415 | -0.093 63 | 9.941 | 2.373 | |
| 价值函数 | 107.092 | 29.686 5 | |||||
由辨识结果和飞行数据可以得到。
1) 如表 2所示,相对比较Model B来说,Model A的价值函数过高,说明辨识结果拟合实验数据的效果一般。Model A的价值参数很难降低,一种假设是因为Model A的模型结构并不合适,无法匹配真实的动力学模型,所以辨识精度有限。在Model A中,动力学模型视直升机和三轴陀螺仪部件为一整体,意味着辨识出来的各项导数是考虑陀螺仪之后的有偏移的数值。因为陀螺仪有自己的角速率反馈控制,所以全机模型的阶次应当比单纯直升机挥舞模型的阶次要高。挥舞模型引入的是一阶模型,如考虑增加陀螺仪的一阶反馈,整体挥舞模型应为二阶。
为了验证以上假设的可靠性,进行如下推导。首先同理于本文1.3节的3阶段尾桨动力学分析方法,假设陀螺仪为一个角速率反馈控制。引入三阶段分析,以纵向动力学为例:
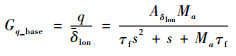
|
(36) |
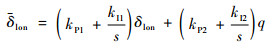
|
(37) |
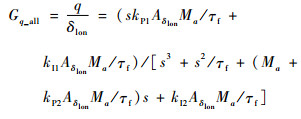
|
(38) |
式中:Gq_base为纵向动力学的基底模型,是由挥舞方程和机体动力学方程推导而来,含有二阶特性;Gq_gyro为陀螺仪的反馈动力学模型。因为δlon和δlon都是标准化的操纵值,所以kP1是一个可定义的参数,这里定义kP1=1。通过Gq_base和Gq_gyro可以推导出Gq_all。式(38)中有两点值得注意:一是分子的一次项系数AδlonMa/τf,二是分母的二次项系数1/τf,这2个位置的参数只含有基底模型动力学的信息。
然后对比一下携带伺服小翼的挥舞模型。由文献[3]可以提取出携带小翼的纵向挥舞模型:
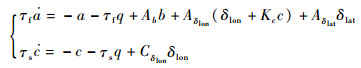
|
(39) |
式中:a为纵向挥舞角;c为伺服小翼挥舞角。由于小翼角度和桨距角之间有机械联动装置,所以式(39)的挥舞方程在δlon处考虑小翼的操纵效应Kcc,Kc为小翼挥舞系数。τs为伺服小翼时间常数。
通过引入机体动力学方程,提取出纵向主要响应如下:
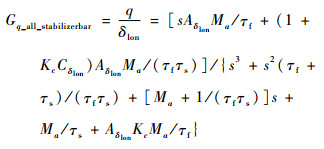
|
(40) |
对比携带陀螺仪的纵向传递函数(式(38))和携带小翼的纵向传递函数(式(40)),发现它们有同样的阶数,说明陀螺仪的角速率反馈动力学是一种合理的假设。陀螺仪是用电子控制的方式来稳定直升机的,拓宽旋翼时间常数,减慢旋翼的响应频率,使旋翼易于操纵,这与伺服小翼有相同作用。通过对比分子一次项系数和分母二次项系数,由于小翼的响应比较慢,τs是τf的10倍,则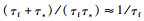
应用式(38),同理推导出横向传递函数,可以对纵向及横向分别进行单通道辨识,通过辨识结果可以提取出基底模型的主要参数(Model A)的主要参数:纵向参数
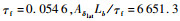
可以发现,由Model A提取的基底模型参数与Model B辨识出来的结果是相一致的。也就是说,通过以上方法证明,对于Model A的辨识,应该再增加一阶挥舞的阶次,来匹配真实的动力学响应。变一阶挥舞方程为二阶挥舞方程。
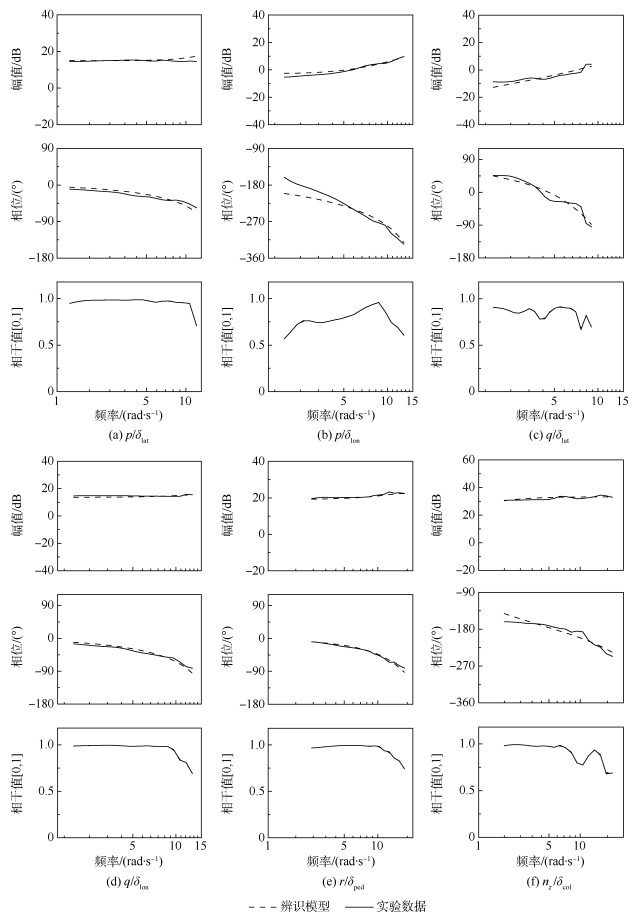
2) 实验中飞行数据的频域信息展现在图 4与图 5中(实线),由图中可以看出,Model B的相干值参数要高于Model A,特别是在高频领域。在Model A中,专业操纵手飞行的辨识数据,在高频区域,相干值参数0.6以上的频率最高为13 rad/s,而在Model B中,高质量频域数据可以达到30 rad/s并保持较高的相干值参数。飞行数据的质量,不管是主轴响应还是轴外响应,比文献[8]中都要好。也就是说,三轴陀螺仪在其中起到了增加飞行数据有效带宽的重要作用。飞行数据频率范围越宽,会包含更多的动力学信息,那么也会让辨识的模型更加贴近真实情况。同样,飞行数据中越高的高频特性也会让高阶模型的辨识变得有意义,因为高阶模型的细节信息主要存在于高频区域,应用高阶模型来辨识可以获得更高的高频贴合度,使模型在更宽的频域范围内更加贴近于真实的动力学特性。因此结合问题一的解决方案,这里引入二阶挥舞方程,来同时解决2个问题。忽略陀螺仪的真实反馈参数,而用二阶挥舞方程参数来代替陀螺仪在Model A中引起的二阶效应。配置二阶挥舞项
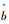
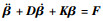
|
| 图 4 Model A 13阶高阶模型频域辨识结果与悬停实验数据对比 Fig. 4 Comparison of frequency-domain identification results of 13-state high-order model with experimental hover data for Model A |
|
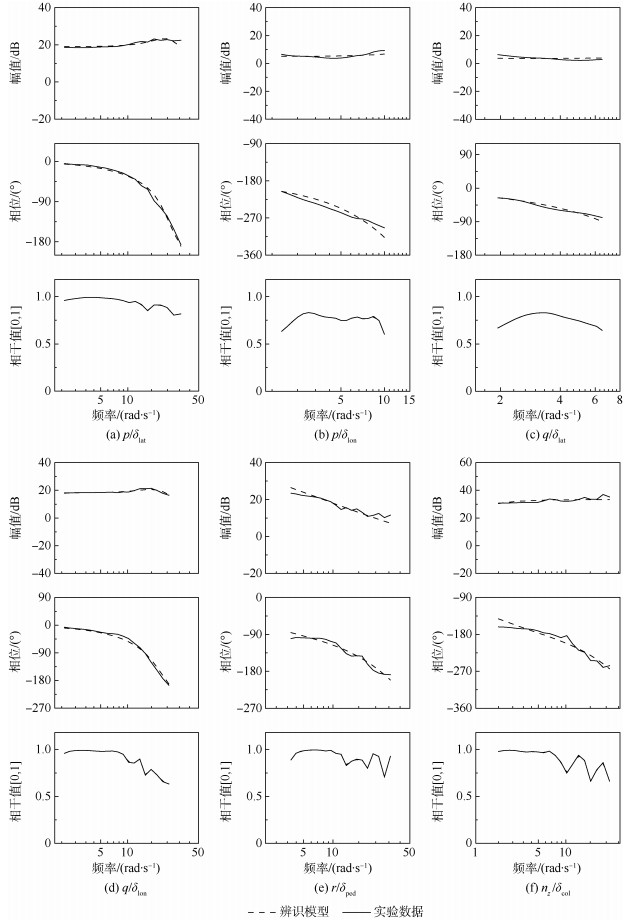
| 图 5 Model B 13阶高阶模型频域辨识结果与悬停实验数据对比 Fig. 5 Comparison of frequency-domain identification results of 13-state high-order model with experimental hover data for Model B |

|
(41) |
再增加机体动力学方程,Model A和Model B新的状态变量变分别为
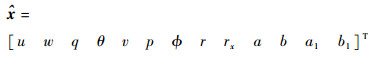
|
(42) |

|
(44) |
采用二阶挥舞方程以后,双系统Model A和Model B的全机模型均为13阶次。然后对此高阶模型进行频域系统辨识。
3.2 双系统高阶模型辨识结果高阶模型的辨识结果见表 3。通过对比表 2 CR%和敏感度参数,可以发现增加二阶挥舞方程以后,13阶次模型的辨识结果在Model A和Model B都表现更优。单独对比纵横向耦合模型,表 2结果中的价值函数为107.092(Model A)和29.686 5(Model B),而高阶模型(式(41))辨识结果,价值函数降低为36.231 2(Model A)和27.380 2(Model B),Model A辨识结果改善更加明显。在表 3全机模型辨识结果中,价值函数为49.098 9(Model A)和39.907 8(Model B),说明高阶模型在全机4个通道方向都具有高可靠性。对比Model B模型,Model A有更大的时间常数τf,更小的旋翼力矩导数Ma和Lb,预示着更稳定的直升机总体状态。图 4和图 5展示了高阶模型在频域辨识中的结果,曲线对比辨识模型与实验数据。通过曲线可以看出,在主轴响应p/δlat和q/δlon中,Model A IDM与Model B IDM均与实验数据贴合良好,Model B优于Model A,尤其在高频区域10~30 rad/s,Model B的高阶结构很好地表现了数据高频信息。在纵横向的轴外方向p/δlon和q/δlat,由于飞行数据的质量有限,双系统线性模型在有限的频率范围内,很好地匹配了实验数据。在垂向方向,因为三轴陀螺仪没有垂向的增稳作用,所以双系统Model A和Model B在垂向导数参数上保持一致。
| 参数 | Model A | Model B | |||||
| 数值 | CR/% | 敏感度/% | 数值 | CR/% | 敏感度/% | ||
| τf | 0.071 30 | 7.425 | 0.681 8 | 0.055 60 | 8.204 | 0.856 0 | |
| Xu | -0.060 20c | -0.060 20c | |||||
| Xa | -9.8a | -9.8a | |||||
| Yv | -0.142 0c | -0.142 0c | |||||
| Yb | 9.8a | 9.8a | |||||
| Zw | -1.714 | 12.09 | 5.473 | -1.714 | 12.67 | 5.795 | |
| Mu | 0.037 10a | 0.045 80a | |||||
| Mv | -0.001 62a | -0.004 42a | |||||
| Ma | 191.3 | 6.422 | 1.714 | 448.4 | 7.465 | 3.006 | |
| Lu | -0.002 21a | -0.002 81a | |||||
| Lv | -0.102 2a | -0.158 0a | |||||
| Lb | 237.2 | 6.753 | 1.735 | 740.9 | 5.905 | 2.530 | |
| Nr | 0.409 3 | 19.85 | 5.892 | -1.084 | 28.2 | 13.47 | |
| Kxr | -403.70 | 21.23 | 1.779 | ||||
| Kxx | -20.47 | 15.36 | 1.965 | ||||
| Ba | -0.426 6 | 4.567 | 1.425 | 0.208 6 | 20.03 | 9.650 | |
| Ab | -0.426 6 | 0.208 6 | |||||
| Aδlat | 0.025 47 | 7.875 | 2.553 | -0.032 70 | 24.62 | 5.610 | |
| Aδlon | -0.343 2 | 6.999 | 1.430 | -0.456 8 | 7.78 | 1.78 | |
| Bδlat | 0.391 3 | 7.242 | 1.094 | 0.504 6 | 8.011 | 1.655 | |
| Bδlon | -0.021 31 | 23.06 | 7.520 | -0.053 30 | 18.46 | 4.161 | |
| Zδcol | -45.87 | 4.251 | 1.925 | -45.87 | 4.253 | 1.944 | |
| Nδcol | -10.58 | 19.93 | 9.765 | 0b | |||
| Nδped | 176.01 | 11.47 | 1.874 | 75.28 | 2.844 | 3.778 | |
| 价值函数 | 49.098 9 | 39.907 8 | |||||
| 注:上标a表示理论值;b表示由模型结构考虑移除的参数;c表示单独辨识参数并在模型中固定不变。 | |||||||
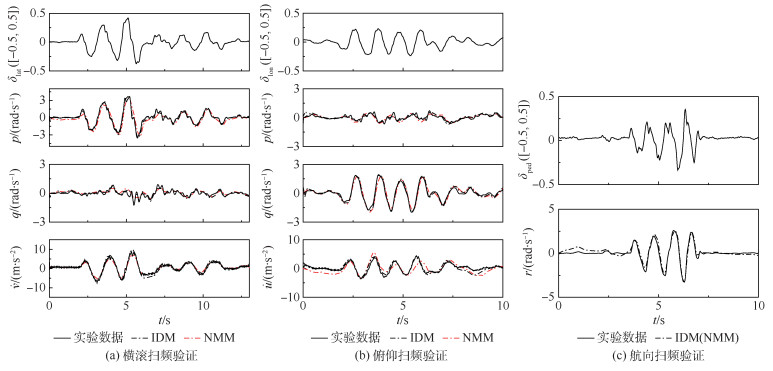
图 6和图 7展示了高阶模型时域验证的结果,通过输入几组悬停扫频飞行数据的控制信号,双系统Model A和Model B的IDM模型对于仿真直升机姿态响应有很高的精确度。图中(δlat, δlon, δcol, δped)为操纵输入。对于航向通道,由三阶段辨识法获得的尾桨动力学模型在Model A和Model B的扫频数据段都有良好的拟合效果。值得注意的是,在航向时域数据的无信号输入段,Model B IDM无法像Model A IDM一样保持直线无信号状。这是因为陀螺仪的锁尾功能是由非线性模块控制,而本文中Model B IDM为线性模型,无法捕捉到非线性的特征。应用2.2节非线性-线性模型结合修正方法,NMM的主要修正参数展现在表 4中,经验证Ma/Lb=Iyy/Ixx。表 3中的轴外耦合项参考NMM理论计算结果。图 6和图 7展示了NMM的仿真结果(红线),因为非线性建模针对的是基底模型Model B,所以NMM的仿真结果主要展现在图 7中。航向的NMM和IDM都利用三阶段辨识法,参数相同,所以不做重复绘图。通过时域仿真分析,可以看出修正后的NMM有很高的仿真精度,但是对比IDM来说,NMM的仿真效果并没有IDM好,主要因为NMM的非线性参数众多,一些微小的差别会积累最终造成总体细节的偏离,目前IDM和NMM的精度对于设计控制器来说已经足够。

|
| 图 6 Model A 13阶高阶模型时域仿真结果与悬停实验数据对比 Fig. 6 Comparison of time-domain simulation results of 13-state high-order model with experimental hover data for Model A |
|
| 图 7 Model B 13阶高阶模型时域仿真结果与悬停实验数据对比 Fig. 7 Comparison of time-domain simulation results of 13-state high-order model with experimental hover data for Model B |
| 参数 | 数值 |
| a0 | 5.75 |
| Kcol | 0.293 2 |
| Kβ | 160.57 |
| Ixx | 0.396 |
| Iyy | 0.653 |
| ΔXu | -0.041 |
| ΔYv | -0.048 5 |
表 5将JR700获得的双系统线性模型的主要参数与3种小型无人直升机进行对比,可以看出基底模型Model B有着更高的响应频率。而借助于三轴陀螺仪的稳定功能,Model A的运动灵活度得到了控制。因为JR700上安装的陀螺仪被设为3档sport模式,所以JR700相对比其他3种直升机,稳定性略差,而灵活性较高。
| 参数 | JR700 13阶 | Raptor 50 | X-cell | HeLion | |
| Model A | Model B | ||||
| τf | 0.071 30 | 0.055 60 | 0.043 | 0.052 | |
| τs+τf | 0.127 | 0.272 | 0.299 | ||
| Lb | 237.2 | 740.9 | 735.5 | 320 | 583.5 |
| Ma | 191.3 | 448.4 | 228 | 204 | 265.3 |
| Aδlat | 0.025 47 | -0.032 70 | 0.008 9a | 0 | 0 |
| Aδlon | -0.343 2 | -0.456 8 | -0.242 2a | -0.53a | -0.42a |
| Bδlat | 0.391 3 | 0.504 6 | 0.031 5a | 0.42a | 0.4a |
| Bδlon | -0.021 31 | -0.053 30 | -0.011 2a | 0 | 0 |
| 注:上标a表示原始数值[3, 7-8]按本文单位标准换算。 | |||||
表 6展示了双系统线性模型的特征根及模态情况,二阶特征根以
| 模态 | 13阶Model A | 13阶Model B |
| 俯仰耦合模态 | [0.673 7, 14.666 0] | [0.426 1, 21.621 4] |
| 滚转耦合模态 | [0.285 9, 14.593 5] | [0.328 8, 26.942 2] |
| 航向模态 | [0.504 5, 19.883 2] | (-1.084 0) |
| 垂向模态 | (-1.713 6) | (-1.713 6) |
| 纵向速度模态 | [0.257 8, 0.139 7] | [0.357 6, 0.192 2] |
| 横向速度模态 | [0.240 8, 0.256 6] | [0.239 0, 0.131 9] |
至此本文给出了8.1 kg JR700 3D直升机在三轴陀螺仪增稳作用下,悬停状态的基底和全机的双系统线性模型。应用高阶挥舞模型进行频域系统辨识达到了良好的辨识效果。本文同时给出了悬停状态的线性和NMM,优化了尾桨动力学辨识过程,给出的模型更深入地展现了携带三轴陀螺仪的小型无人直升机的飞行动力学特征,模型数据将非常有助于控制系统的研究。
4 结论本文重点考虑携带三轴陀螺仪增稳的小型无人直升机在悬停飞行中的模型辨识问题。得到以下结论:
1) 在辨识实验中同时记录陀螺仪之前和之后的操纵信号,分别作为操纵输入,进行频域系统辨识分析,可以同时得到双系统线性模型。通过数据得知,一阶挥舞方程不适用于Model A动力学特性,陀螺仪的反馈作用使挥舞动力学的高阶效应更加明显。而Model B的飞行数据具有更高质量的高频数据,利用Model B飞行数据辨识直升机基底模型有利于提高模型高频区域的精确度。
2) 尾桨动力学的辨识应用三阶段辨识法。第1阶段为基底模型,可以通过航向辨识实验得到;第2阶段为陀螺仪模型,应用PI反馈假设,可以通过地面扫频实验得到;第3阶段为整体增稳模型。三阶段辨识法获得辨识结果有很高的频域辨识精度,时域验证中基底模型和整体模型均能很好地仿真拟合实验数据。
3) 除了线性模型以外,同时进行非线性建模,并利用非线性-线性模型结合修正方法提高了线性模型和NMM的精度。除了挥舞动力学方程及航向动力学以外,NMM修正7个非线性参数,总体来讲修正后NMM在悬停状态仿真效果表现优异。
4) 在频域辨识过程中,增加二阶挥舞项的13阶次双系统线性模型相比11阶次双系统线性模型有更好的辨识效果,辨识结果价值函数更低,模型可靠性更高,高阶频域贴合程度更好。模型具有2个主要模态,俯仰耦合模态和滚转耦合模态,符合同种类型直升机特点。相比Model A和Model B机动灵活性更高。
致谢 感谢米兰理工大学(Politecnico di Milano) M.Lovera教授在论文撰写过程中提出的宝贵意见与建议,感谢实验室徐安安与刘永辉同学在飞行试验过程中给予的大力帮助。
| [1] |
METTLER B, TISCHLER M B, KANADE T. System identification modeling of a small-scale unmanned rotorcraft for flight control design[J]. Journal of the American Helicopter Society, 2002, 47(1): 50-63. DOI:10.4050/JAHS.47.50 |
| [2] |
杨帆, 熊笑, 陈宗基, 等. 超小型直升机动力学模型的建模、辨识与验证[J]. 北京航空航天大学学报, 2010, 36(8): 913-917. YANG F, XIONG X, CHEN Z J, et al. Modeling, system identification and validation of small rotorcraft-based unmanned aerial vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8): 913-917. (in Chinese) |
| [3] |
METTLER B. Identification modeling and characteristics of miniature rotorcraft[M]. New York: Kluwer Academic Publishers, 2002: 53-90.
|
| [4] |
GAVRILETS V, METTLER B, FERON E.Nonlinear model for a small-size acrobatic helicopter[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: AIAA: 2001: 4333.
|
| [5] |
GAVRILETS V, MARTINOS I, METTLER B, et al.Control logic for automated aerobatic flight of a miniature helicopter[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: AIAA, 2002: 4834.
|
| [6] |
KHALIGH S P, FAHIMI F, ROBERT K C. A system identification strategy for nonlinear model of small-scale unmanned helicopters[J]. Journal of the American Helicopter Society, 2016, 61(4): 1-13. |
| [7] |
CAI G, CHEN B M, LEE T H, et al.Comprehensive nonlinear modeling of an unmanned-aerial-vehicle helicopter[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: AIAA, 2008: 7414.
|
| [8] |
BHANDARI S, COLGREN R. High-order dynamics models of a small UAV helicopter using analytical and parameter identification techniques[J]. Journal of the American Helicopter Society, 2015, 60(2): 1-10. |
| [9] |
GRAUER J, CONROY J, HUBBARD J, et al. System identification of a miniature helicopter[J]. Journal of Aircraft, 2009, 46(4): 1260-1269. DOI:10.2514/1.40561 |
| [10] |
KAPILTA T T, DRISCOLL J T, DIFTLER M A, et al.Helicopter simulation development by correlation with frequency sweep flight test data[C]//American Helicopter Society 45th Annual Forum Proceedings.Boston, MA: American Helicopter Society (AHS), 1989: 631-643.
|
| [11] |
PANIZZA P, RICCARDI F, LOVERA M. Black-box and grey-box identification of the attitude dynamics for a variable-pitch quadrotor[J]. IFAC-PapersOnLine, 2015, 48(9): 61-66. DOI:10.1016/j.ifacol.2015.08.060 |
| [12] |
BERGAMASCO M, LOVERA M.Rotorcraft system identification: An integrated time-frequency domain approach[C]//Advances in Aerospace Guidance, Navigation and Control.Berlin: Springer, 2013: 161-181.
|
| [13] |
DE MENDONCA C B. Flight vehicle system identification:A time-domain methodology[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(3): 737-738. |
| [14] |
TISCHLER M B, REMPLE R K. Aircraft and rotorcraft system identification[M]. Reston: AIAA, 2006: 321-491.
|
| [15] |
LA CIVITA M, PAPAGEORGIOU G, MESSNER W C, et al. Design and flight testing of an H∞ controller for a robotic helicopter[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 485-494. |
| [16] |
李继广, 陈欣, 李亚娟, 等. 飞翼无人机机动飞行非线性鲁棒控制方法[J]. 北京航空航天大学学报, 2018, 44(1): 89-98. LI J G, CHEN X, LI Y J, et al. Nonlinear robust control method for maneuver flight of flying wing UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(1): 89-98. (in Chinese) |
| [17] |
TISCHLER M, CAUFFMAN M.Comprehensive identification from frequency responses, Vol.2: User's manual: NASA CP 10150[R].Washington, D.C.: NASA, 1994.
|
| [18] |
WU W. Identification method for helicopter flight dynamics modeling with rotor degrees of freedom[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1363-1372. DOI:10.1016/j.cja.2014.10.002 |
| [19] |
LA CIVITA M.Integrated modeling and robust control for full-envelope flight of robotic helicopters[D].Ann Arbor, MI: Carnegie Mellon University, 2002: 21-98.
|
| [20] |
TANG S, ZHENG Z, QIAN S, et al. Nonlinear system identification of a small-scale unmanned helicopter[J]. Control Engineering Practice, 2014, 25: 1-15. DOI:10.1016/j.conengprac.2013.12.004 |
| [21] |
PADFIELD G D. Helicopter flight dynamics[M]. Oxford: Blackwell Publishing, 2008: 87-184.
|
| [22] |
HEFFLEY R K, MNICH M A.Minimum-complexity helicopter simulation math model: NASA-11665[R].Washington, D.C.: NASA, 1988.
|
| [23] |
CAI G, CHEN B M, LEE T H. Unmanned rotorcraft systems[M]. Berlin: Springer, 2011: 70-111.
|
| [24] |
LEISHMAN G J. Principles of helicopter aerodynamics[M]. Cambridge: Cambridge University Press, 2006: 115-169.
|
| [25] |
CAI G, CHEN B M, PENG K, et al. Modeling and control of the yaw channel of a UAV helicopter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(9): 3426-3434. DOI:10.1109/TIE.2008.926780 |
| [26] |
CHEN R T N.Effects of primary rotor parameters on flapping dynamics: NASA-1431[R].Washington, D.C.: NASA, 1980.
|



