卫星是目前应用最为广泛的航天器,卫星的姿态控制系统故障会导致严重的后果,其中执行器由于长期处于工作状态中很容易发生故障,因此卫星姿态控制系统的执行器故障诊断问题很有研究价值。很多故障在早期表现很微小[1],通常会被系统扰动噪声掩盖,因此微小故障的检测对于故障的早期诊断有重要意义。
基于解析模型的方法,尤其是观测器方法,在卫星姿态控制系统故障诊断中取得了很多成果,也是目前研究最为活跃的方法[2-3]。基于解析模型的故障诊断易受到扰动干扰,为解决这个问题,文献[4-5]研究了鲁棒观测器,力图使观测器残差对扰动解耦,但是由于扰动无法完全解耦,对于微小故障的检测达不到满意的效果。与鲁棒观测器类似,文献[6-8]提出的学习观测器虽然对空间干扰和测量噪声具有鲁棒性,但是也没有完全与故障残差解耦。文献[9-10]研究了自适应观测器方法,通过对故障的自适应估计使得观测结果对扰动鲁棒,但是只考虑了输入端的扰动力矩,而没考虑测量敏感器的噪声。
鉴于解析模型难以解决扰动问题,神经网络因为其优秀的非线性建模能力被用于故障诊断。文献[11-12]提出应用神经网络对系统中的非线性部分进行估计,放宽了对系统的匹配条件,但是没有充分利用系统的结构知识;文献[13-15]提出了应用神经网络直接估计故障的方法,但是仍然没有考虑微小故障的检测问题。
干扰观测器[16-17]通常用来补偿控制系统内的模型误差等扰动,参考其补偿干扰的思路,本文提出了一种基于神经网络干扰观测器的微小执行器故障检测方法。利用卫星姿态控制系统内的冗余关系,通过构建干扰观测器对系统内的测量误差、扰动等进行估计,对基于解析模型的故障检测观测器进行扰动补偿,实现对微小故障的检测。并利用Lyapunov理论证明了所设计的干扰观测器的稳定性。
1 问题描述 1.1 姿态控制系统建模考虑如图 1所示的三轴稳定卫星姿态控制系统,其中敏感器为陀螺和星敏感器;执行器为反作用飞轮;控制算法采用非线性四元数反馈控制律。卫星姿态控制系统可以分为运动学子系统和动力学子系统[18]。运动学子系统包括陀螺、星敏感器和运动学过程,反映了卫星姿态角与角速度间的关系;动力学子系统包括反作用飞轮、陀螺和动力学过程,反映了卫星受到的控制力矩与角速度间的关系。仅考虑反作用飞轮可能出现故障的情况。
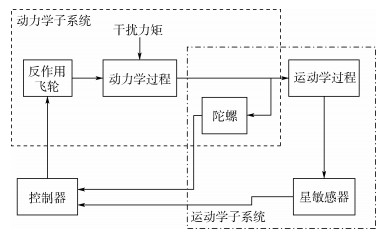
|
| 图 1 卫星姿态控制系统 Fig. 1 Satellite attitude control system |
由四元数描述的姿态运动学方程为[18]
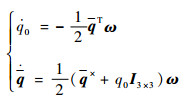
|
(1) |
式中: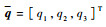
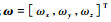

|
(2) |
选取
|
(3) |
式中:


|
(4) |
考虑陀螺的测量误差,则运动学子系统表达式为
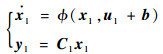
|
(5) |
式中:
将卫星本体看作刚体,则由刚体运动的动量矩公式可得到卫星姿态动力学方程[18]为

|
(6) |
式中:H为卫星的角动量;
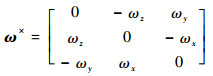
|
(7) |
角动量H可以表示为


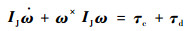
|
(8) |
其中:

选取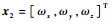
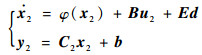
|
(9) |
其中:
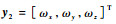
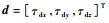
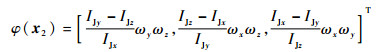
|
(10) |
系统的输入矩阵B、输出矩阵E和扰动分布矩阵C2表达式如下:
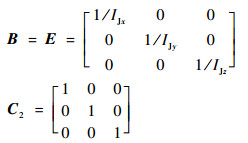
|
在进行问题描述前,做以下合理假设。
假设1 假设卫星工作在小角度机动状态下,因此式(3)和式(9)中的非线性函数均为满足Lipschitz条件的Lipschitz函数,即
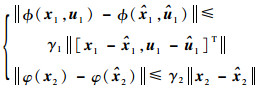
|
(11) |
式中:γ1和γ2分别为Lipschitz系数;
假设2 不同部件不会同时发生故障。
假设3 故障和扰动均有界,且故障的变化速率有界。
考虑2类故障:加性故障和乘性故障。相应的故障模型为
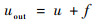
|
(12) |

|
(13) |
式中:u为正常信号;uout为故障后信号;f为故障参数,可以是一个突变常数,也可以是一个时变参数;a为某正常参数。
则故障后的动力学子系统模型可以表示为
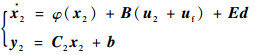
|
(14) |
式中:
观察式(14)可知,系统中存在模型不确定性、扰动以及测量误差等干扰,因此基于故障观测器的检测方法对于混杂在干扰中的微小故障检测能力很弱。本文的工作即是提出一种基于神经网络干扰观测器的方法对系统内存在的干扰进行估计,并对故障观测器进行干扰补偿,提高故障观测器的检测能力。如图 1所示,卫星姿态控制系统可以分为运动学子系统和动力学子系统2个部分。运动学子系统能反映陀螺和星敏感器间的关系,动力学子系统能反映陀螺和反作用飞轮间的关系。因此可以分别利用2个子系统间的冗余关系对陀螺测量误差和干扰力矩进行估计,进而达到补偿故障观测器的目的。
2 微小故障检测方法基于神经网络干扰观测器的微小执行器故障检测系统框图如图 2所示,q为姿态四元数,r为检测残差。其中利用运动学子系统估计陀螺干扰;利用动力学子系统以及陀螺干扰估计结果,估计干扰力矩;最后用得到的2个扰动估计值去补偿故障检测观测器。
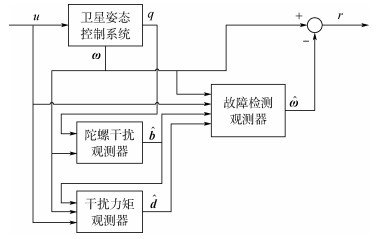
|
| 图 2 故障检测观测器框图 Fig. 2 Block diagram of fault detection observer |
考虑无故障情况下的运动学子系统状态方程式(3),采用神经网络对陀螺的测量误差进行估计,可以得到的干扰观测器为
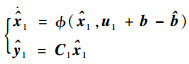
|
(15) |
式中: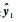


|
(16) |
其中: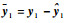


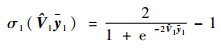
|
(17) |
根据神经网络的逼近特性,存在一组理想权值和阈值使得b可以表示为
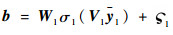
|
(18) |
式中:
由式(5)和式(15)可以得到观测误差动态方程为
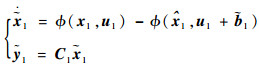
|
(19) |
式中:


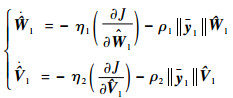
|
(20) |
式中:η1和η2为神经网络的学习率;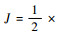

定义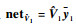

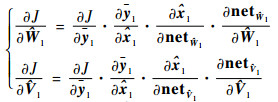
|
(21) |
记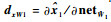

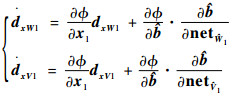
|
(22) |
则得到最终的神经网络权值更新律为
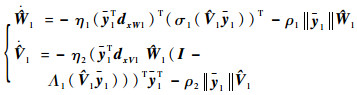
|
(23) |
式中: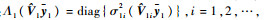
定理1 考虑如式(5)的动态系统,构造如式(15)的干扰观测器,以式(19)定义观测误差。如果采用式(23)为神经网络的权值更新律,则观测误差一致有界,且神经网络权值估计误差有界。
证明 选择如下正定Lyapunov函数:

|
(24) |
其中: 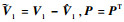

|
(25) |
式中:A为Hurwitz矩阵;Q为对称正定矩阵。对式(24)进行微分可得

|
(26) |
式中:
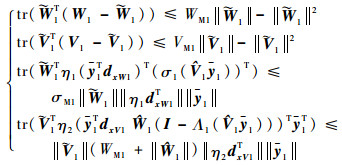
|
(27) |
将式(11)和式(27)代入式(26),可以得到
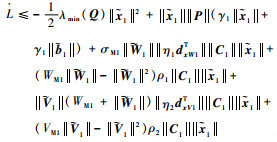
|
(28) |
于是,可以得到如下保证
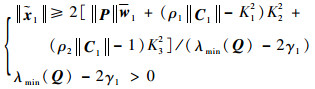
|
(29) |
式中:
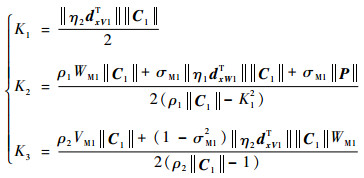
|
(30) |
证毕
2.2 基于动力学的干扰力矩观测器设计考虑无故障情况下的动力学子系统状态方程式(9),采用神经网络对陀螺的测量误差进行估计,可以得到如下的干扰观测器:

|
(31) |
由2.1节中基于运动学的陀螺干扰观测器式(15)得到。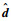
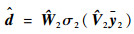
|
(32) |
式中:隐层神经元的传递函数σ2(·)与σ1(·)相同。同样地,根据神经网络的逼近特性,存在一组理想权值和阈值使得d可以表示为

|
(33) |
式中: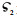
由式(9)和式(31)可以得到观测误差动态方程如下:

|
(34) |
式中:

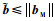
与式(23)类似,给出如下权值更新率:
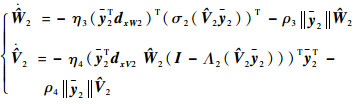
|
(35) |
定理2 考虑如式(9)形式的动态系统,构造如式(31)的干扰观测器,以式(34)定义观测误差。如果采用式(35)为神经网络的权值更新律,则观测误差一致有界,且神经网络权值估计误差有界。
证明过程参照定理1。
2.3 微小故障检测观测器设计为检测执行器的微小故障,在2个干扰观测的基础上,针对式(9)设计如下执行器微小故障检测观测器:
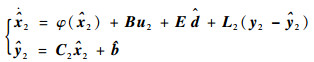
|
(36) |
得到的观测误差动态方程为

|
(37) |
式中: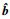
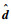

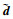
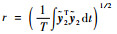
以下定理保证所设计故障观测器的稳定性。
定理3 对于给定常数γ0,如果存在矩阵M和对称正定矩阵Q满足:

|
(38) |
则观测器的增益矩阵可选为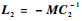
证明 以运动学子系统故障检测观测器(36)为例,选择如下正定Lyapunov函数:

|
(39) |
对其求导可得
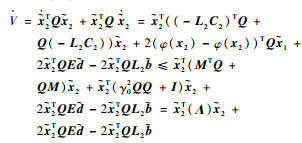
|
(40) |
式中:


|
(41) |
证毕
3 数值仿真分析 3.1 仿真参数设定卫星姿态控制系统仿真框架如图 1所示。控制器采用非线性四元数反馈算法,比例系数Kp=[40, 40, 40]T,微分系数Kd=[1 000, 1 000, 1 000]T。卫星的转动惯量矩阵为IJ=diag{930, 800, 1 070} kg·m2;初始轨道角速度为ω0=[0, 1.2×10-6, 0]T rad/s;初始姿态角速度ω(0)=[0, 0, 7.3]T×10-5 rad/s;初始姿态为Q0=[0.978 6, -0.070 4, -0.179 8, 0.070 4]T;干扰力矩为
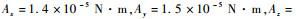
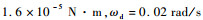
系统仿真长度为400 s,步长为0.01 s,设置故障时刻为200 s。设置常值故障、斜坡故障和乘性故障3种故障,故障案例1为x轴的常值故障,参数为
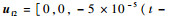


|
图 3~图 5分别为各轴受到的干扰力矩估计情况,ε为估计误差。可以看出神经网络的估计误差在100 s左右收敛到0附近,能够对干扰力矩进行很好的跟踪估计。

|
| 图 3 x轴干扰力矩估计 Fig. 3 Estimated disturbance torque in x axes |

|
| 图 4 y轴干扰力矩估计 Fig. 4 Estimated disturbance torque in y axes |

|
| 图 5 z轴干扰力矩估计 Fig. 5 Estimated disturbance torque in z axes |
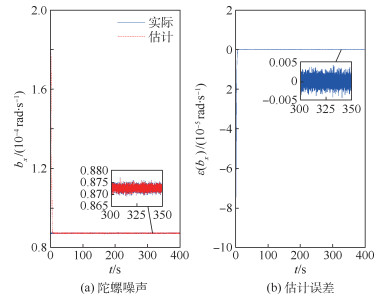
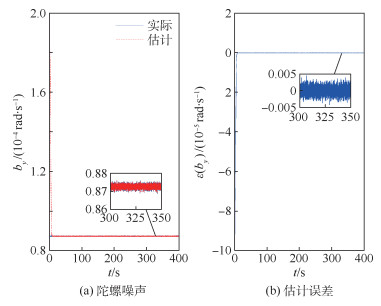
图 6~图 8分别为各轴陀螺的测量误差估计情况,bx、by、bz为各轴陀螺噪声。可以看出相对力矩干扰观测器,陀螺干扰观测器的收敛速度很快,这是因为陀螺干扰观测器中只有陀螺测量误差为干扰源,而力矩干扰观测器中不仅在输入端存在力矩干扰,还在输出端存在测量干扰。
|
| 图 6 x轴陀螺噪声估计 Fig. 6 Estimated noise of gyro in x axes |
|
| 图 7 y轴陀螺噪声估计 Fig. 7 Estimated noise of gyro in y axes |

|
| 图 8 z轴陀螺噪声估计 Fig. 8 Estimated noise of gyro in z axes |
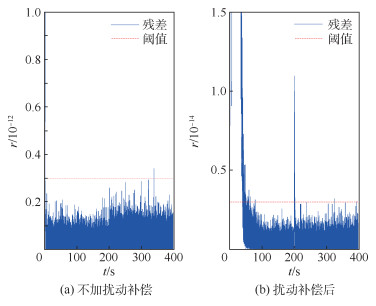
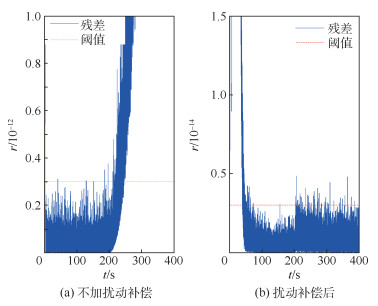
对3类不同类型故障的检测结果如图 9~图 11所示。其中,图 9为对故障参数为uf1=[-3×10-4, 0, 0]T的x轴执行器常值故障检测结果;图 10对故障参数为uf2=[0, 0, -5×10-5(t-200)]T的z轴执行器斜坡故障检测结果;图 11为对故障参数为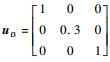
|
| 图 9 故障案例1检测残差 Fig. 9 Detection residual of fault case 1 |
|
| 图 10 故障案例2检测残差 Fig. 10 Detection residual of fault case 2 |

|
| 图 11 故障案例3检测残差 Fig. 11 Detection residual of fault case 3 |
图 9(a)、图 10(a)和图 11(a)的结果显示,不加扰动补偿的情况下,除斜坡故障在幅值增大一定程度后可以被检测外,其他2个故障都被掩盖在扰动产生的残差中。图 9(b)、图 10(b)和图 11(b)的结果显示,进行扰动补偿后,降低了检测阈值,且3个故障均可及时检测出来,其中前100 s为动态调整过程,不做讨论。
由3个不同故障案例的检测结果来看,该方法解决了微小执行器故障的检测问题,但是不能解决故障的隔离、诊断问题,后续还需要进行故障隔离观测器等工作。
4 结论1) 通过利用姿态控制系统内冗余关系设计干扰观测器,对故障检测器进行扰动补偿,从而实现了对微小执行器故障的检测,但是不能进行故障隔离等。
2) 干扰观测器采用神经网络进行设计,证明了采用的自适应权值更新律能够保证观测器的稳定性;证明了扰动补偿下的故障检测观测器的稳定性。
3) 以3轴稳定卫星姿态控制系统为例,仿真了本文方法对不同类型的微小执行器故障的检测能力,并与未进行扰动补偿的情况进行了对比。
| [1] |
肇刚, 李泽, 李言俊. 基于TSEOPM的在轨航天器故障预报方法研究[J]. 计算机测量与控制, 2009, 17(12): 2352-2354. ZHAO G, LI Z, LI Y J. Research on method of fault prediction for onboard spacecrafts based on times series event omen pattern mining[J]. Computer Measurement & Control, 2009, 17(12): 2352-2354. (in Chinese) |
| [2] |
苏林, 尚朝轩, 刘文静. 航天器姿态控制系统故障诊断方法概述[J]. 长春理工大学学报(自然科学版), 2010, 33(4): 23-27. SU L, SHANG C X, LIU W J. Survey on the technology of fault diagnosis for spacecraft attitude control system[J]. Journal of Changchun University of Science and Technology(Natural Science Edition), 2010, 33(4): 23-27. DOI:10.3969/j.issn.1672-9870.2010.04.006 (in Chinese) |
| [3] |
CHENG Y, WANG R X, XU M Q. Simultaneous state and actuator fault estimation for satellite attitude control systems[J]. Chinese Journal of Aeronautics, 2016, 29(3): 714-721. DOI:10.1016/j.cja.2016.04.010 |
| [4] |
GAO C, DUAN G R. Robust adaptive fault estimation for a class of nonlinear systems subject to multiplicative faults[J]. Circuits, Systems, and Signal Processing, 2012, 31(6): 2035-2046. DOI:10.1007/s00034-012-9434-x |
| [5] |
MONDAL S, CHAKRABORTY G, BHATTACHARYY K. LMI approach to robust unknown input observer design for continuous systems with noise and uncertainties[J]. International Journal of Control, Automation and Systems, 2010, 8(2): 210-219. DOI:10.1007/s12555-010-0205-9 |
| [6] |
张科, 韩治国, 郭小红, 等. 航天器姿控系统的PD型学习观测器故障重构[J]. 航空学报, 2017, 38(6): 320629. ZHANG K, HAN Z G, GUO X H, et al. PD-type learning observer based fault reconstruction for spacecraft attitude control systems[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(6): 320629. (in Chinese) |
| [7] |
贾庆贤, 张迎春, 陈雪芹, 等. 卫星姿态控制系统故障重构观测器设计[J]. 宇航学报, 2016, 37(4): 442-450. JIA Q X, ZHANG Y C, CHEN X Q, et al. Observer design for fault reconstruction in satellite attitude control system[J]. Journal of Astronautics, 2016, 37(4): 442-450. DOI:10.3873/j.issn.1000-1328.2016.04.010 (in Chinese) |
| [8] |
贾庆贤, 张迎春, 沈毅, 等. 基于迭代学习-未知输入观测器的卫星姿控系统鲁棒故障重构[J]. 系统工程与电子技术, 2012, 34(1): 120-124. JIA Q X, ZHANG Y C, SHEN Y, et al. Robust fault reconstruction method for satellite attitude control system based on iterative learning-unknown input observer[J]. System Engineering and Electronics, 2012, 34(1): 120-124. DOI:10.3969/j.issn.1001-506X.2012.01.23 (in Chinese) |
| [9] |
岑朝辉, 魏蛟龙, 蒋睿, 等. 基于综合观测器的执行器过程故障量精确诊断[J]. 宇航学报, 2011, 32(6): 1318-1326. CEN C H, WEI J L, JIANG R, et al. Accurate diagnosis on process fault parameters of nonlinear actuator based on adaptive observer and extended state observer[J]. Journal of Astronautics, 2011, 32(6): 1318-1326. DOI:10.3873/j.issn.1000-1328.2011.06.018 (in Chinese) |
| [10] |
胡正高, 赵国荣, 李飞, 等. 基于自适应未知输入观测器的非线性动态系统故障诊断[J]. 控制与决策, 2016, 31(5): 901-906. HU Z G, ZHAO G R, LI F, et al. Fault diagnosis for nonlinear dynamical system based on adaptive unknown input observer[J]. Control and Decision, 2016, 31(5): 901-906. (in Chinese) |
| [11] |
马立玲, 杨英华, 王福利. 一类基于神经网络非线性观测器的鲁棒故障检测和诊断[J]. 控制与决策, 2003, 18(3): 309-316. MA L L, YANG Y H, WANG F L. Robust fault detection and diagnosis based on neural network nonlinear observer[J]. Control and Decision, 2003, 18(3): 309-316. DOI:10.3321/j.issn:1001-0920.2003.03.012 (in Chinese) |
| [12] |
姜寅令, 李艳辉, 王海星. 改进的神经网络观测器在非线性系统中的应用[J]. 吉林大学学报(信息科学版), 2015, 33(4): 471-475. JIANG Y L, LI Y H, WANG H X. Improved neural network state observer designed for nonlinear system[J]. Journal of Jilin University(Information Science Edition), 2015, 33(4): 471-475. DOI:10.3969/j.issn.1671-5896.2015.04.019 (in Chinese) |
| [13] |
TALEBI H A, KHORASANI K. A neural network-based multiplicative actuator fault detection and isolation of nonlinear systems[J]. IEEE Transactions on Control Systems Technology, 2013, 21(3): 842-851. DOI:10.1109/TCST.2012.2186634 |
| [14] |
SHEN Q K, JIANG B, SHI P. Novel neural networks-based fault tolerant control scheme with fault alarm[J]. IEEE Transactions on Cybernetics, 2014, 44(11): 2190-2201. DOI:10.1109/TCYB.2014.2303131 |
| [15] |
LI Q G, FENG Y Z, TONG S C, et al. Fault detection and fault tolerant control of nonlinear systems using neural networks[J]. Information and Control, 1998, 27(6): 440-445. |
| [16] |
王肖, 郭杰, 唐胜景, 等. 吸气式高超声速飞行器鲁棒非奇异Terminal滑模反步控制[J]. 航空学报, 2017, 38(3): 320287. WANG X, GUO J, TANG S J, et al. Robust nonsingular Terminal sliding mode backstepping control for air-breathing hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 320287. (in Chinese) |
| [17] |
骆长鑫, 张东洋, 雷虎民, 等. 输入受限的高超声速飞行器鲁棒反演控制[J]. 航空学报, 2018, 39(4): 321801. LUO C X, ZHANG D Y, LEI H M, et al. Robust backstepping control of input-constrained hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4): 321801. (in Chinese) |
| [18] |
WANG R X, CHENG Y, XU M Q. Analytical redundancy based fault diagnosis scheme for satellite attitude control systems[J]. Journal of the Franklin Institute, 2015, 352(5): 1906-1931. DOI:10.1016/j.jfranklin.2015.02.003 |



