2. 中国兵器工业集团有限公司 导航与控制技术研究所, 北京 100089;
3. 北京机电研究所, 北京 100083
2. Navigation and Control Technology Institute, China North Industries Group Corporation Limited, Beijing 100089, China;
3. Beijing Institute of Electromechanical Technology, Beijing 100083, China
作为陆军主要远程压制武器,远程精确制导火箭炮是炮兵对敌远程精确打击的主要力量。在现代及未来战争中,提高火箭炮自身的生存能力至关重要,其中缩短发射准备时间以提高其快速反应能力是最重要的方向之一。因此,在保证一定精度的前提下,研究发射诸元快速计算问题显得尤为重要。
在制导火箭炮发射前必须对其发射诸元进行快速装定,即在给出炮位和目标点经度、纬度、高程的条件下快速计算火箭炮的射角和射向[1]。制导火箭弹具有一定的机动能力,能有效克服各种随机误差,如初始发射误差、弹体参数误差、气动参数误差和气象误差,因此制导火箭炮的发射诸元装定可简化,不需要输入实际气象文件,除保留药温修正外,取消相关的修正诸元计算。因此,为进一步提高发射诸元的计算精度并有效缩短计算时间,亟需对标准气象条件下发射诸元的快速计算方法进行研究。
计算火箭炮发射诸元的方法有2种:射表法和迭代法。其中,射表法是一种以射表为基础采用插值或数据拟合的方法求解射程对应的基本诸元和修正诸元的处理方法[2]。该方法是目前工程中常用的发射诸元计算方法,存在一定的误差,可在一定范围内满足精度要求。
迭代法是在迭代初值的基础上通过多次求解弹道方程组得到发射诸元的一种计算方法,该方法可对任意发射条件下的发射诸元进行精确计算。与射表法相比,迭代法的计算速度较慢,其计算速度主要取决于弹道模型、迭代初始值和迭代方法。六自由度弹道模型[3]是最为精确的,但在实际计算时必须采用较小的步长,且需要多次迭代计算,所需的计算时间较长,而采用其他的弹道模型又会造成射角的计算精度较低,因此,最大限度地减少迭代次数是提高迭代法计算速度的关键。在给定弹道模型的条件下,迭代次数主要取决于迭代初值和迭代方法。对于迭代初值的选取,一般通过射表法得到,主要采用插值或多项式拟合的方法[2,4]。对于迭代方法,周珞晶等提出了一种改进的迭代计算方法,该方法可以大幅减少射角计算所需的迭代修正次数[5];赵东华等提出了一种基于二分法求根的射角计算方法[6], Chusilp等提出了4种迭代方法,并以M107式榴弹的射角计算为例对比了4种方法的计算速度[7];此外,Charubhun和Chusilp针对多管火箭炮系统的3种射程与射角的关系提出了一种利用六自由度弹道方程组和二分法计算射角的方法[8]。
若不考虑弹体参数误差和气象误差等随机误差影响,射角和无控弹道侧偏的大小由炮位纬度、炮位高程、射向、射程、目标点高程和药温等因素确定,且射角、无控弹道侧偏与上述各影响因素间具有高度非线性的函数关系。综合考虑影响发射诸元的各个因素,研究一种标准气象条件下发射诸元的快速、高精度计算方法,其计算结果既可以直接作为制导火箭炮的装定诸元,又可以作为发射简控和无控火箭弹的火箭炮在实际气象条件下迭代弹道方程组时的初值,具有重要意义。
本文提出了一种基于大样本数据建立射角和无控弹道侧偏代理模型的方法。代理模型是通过对仿真模型的输入参数和输出结果进行拟合而得到的新的数学模型,该数学模型的计算结果可以代替昂贵、耗时的高精度模型的仿真分析结果[9],被广泛应用于实际的工程优化设计中[10]。
以某制导火箭炮为例,进行了发射诸元计算方法的应用研究。首先,运用拉丁超立方抽样(Latin Hypercube Sampling, LHS)[11]进行数值试验设计,并分别运用多项式响应面(Polynomial Response Surface,PRS)、Kriging[12]、径向基函数(Radial Basis Function,RBF)[13]、最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)[14]、超限学习机(Extreme Learning Machine,ELM)[15]和组合代理模型(Ensemble of Surrogate Model,EOSM),进行了基于代理模型的发射诸元计算方法研究,建立了射角、无控弹道侧偏与炮位纬度、炮位高程、射向、射程、目标点高程及药温之间的函数关系;其次,以预测射角为例,统计了各种代理模型的预测时间;然后,为了减小末制导段的舵资源压力,提出了一种射向修正方法,即通过已建立的无控弹道侧偏与各个影响因素的函数关系预测无控弹道侧偏,并根据无控弹道侧偏的预测值和射程计算射向的修正角度,同时对射向修正法的修正效果进行了验证;最后,分析了测试样本数量和训练样本数量对预测精度的影响。
1 代理模型的相关理论 1.1 多项式响应面多项式响应面是一种采用统计学回归分析进行函数拟合的代理模型,具有计算量小、构造简单、鲁棒性良好等特点,在工程产品优化设计中应用较为广泛。为推导和书写方便,假定响应是一维的,则多项式响应面的表达式为
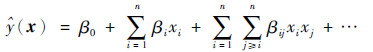
|
(1) |
式中:
Kriging是一种基于统计理论,充分考虑变量空间相关特征的插值技术[12],包含回归模型部分和随机模型部分:
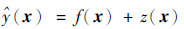
|
(2) |
式中:f(x)为回归模型部分,提供全局近似,且通常为多项式函数;z(x)为随机模型部分,提供局部偏差近似,其均值为零,方差为σ2,协方差为
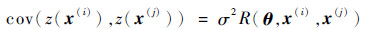
|
(3) |
式中:R(θ, x(i), x(j))为带有参数向量θ的相关函数,表示训练样本点x(i)和x(j)之间的空间相关性。常见的相关函数包括立方函数(Cubic)、指数函数(Exp)、高斯函数(Gauss)、线性函数(Lin)、球形函数(Spherical)和样条函数(Spline)等。此外,文献[16]给出了2种Matern相关函数Matern32和Matern52,表达式分别为
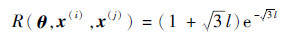
|
(4) |

|
(5) |
式中:
径向基函数模型是以径向基函数为核函数,并通过线性叠加构造出来的模型[13]。正定径向基函数模型的基本形式如下:
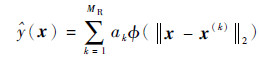
|
(6) |
式中:MR为基函数个数;ak为基函数的加权系数;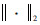
在式(6)中添加一个多项式,即可得到条件正定径向基函数模型的表达式为

|
(7) |
式中:q为径向基函数条件正定的阶数;λd为多项式回归系数;d为多项式阶数。常见的条件正定基函数包括单项式函数(Monomial,MN)、多二次函数(Multi-Quadric,MQ)和薄板样条函数(Thin-Plate Splines,TPS)等。
1.4 最小二乘支持向量机支持向量机是一种建立在统计学习理论的VC维理论和结构风险最小化原则基础上的新的机器学习技术[17],已成功应用于处理非线性回归和分类等实际问题。最小二乘支持向量机是SVM的一种扩展[14],它将不等式约束替代为等式约束,简化了计算,具有出色的预测分析能力。其一般表达式为
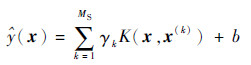
|
(8) |
式中:MS为支持向量的个数;γk为权向量γ的第k个权值;K(x, x(k))为核函数,常见的核函数包括线性函数(Lin)、多项式函数(Polynomial)和高斯函数(Gauss)等;b为常数项。
1.5 超限学习机超限学习机是由黄广斌等提出的一种新型快速学习算法[15]。对于一个具有ME个隐层节点的单隐层神经网络,表达式为

|
(9) |
式中:μk为隐含层到输出层的权值;g(·)为激活函数,常用的激活函数包括径向基传递函数(Radbas)、Sigmoid函数(Sigmoid)、正弦函数(Sine)、双曲正切函数(Tanh)和三角形基函数(Tribas)等;ηk = [ηk1, ηk2, …, ηkn]为输入层到隐含层的权值向量;ck为隐含层偏置。
1.6 组合代理模型组合代理模型,也称加权平均代理模型(weighted average surrogate model),是近似建模领域新的研究热点,其一般形式为
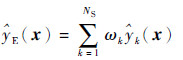
|
(10) |
式中: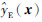
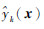
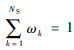
计算权系数是构建EOSM的关键环节,目前典型的权系数计算方法有最优权系数法、反比例平均化法和启发式计算法等[18]。本文采用最优权系数法,该方法将权系数的计算过程看作一个优化问题,使用的优化方法是多变异位自适应遗传算法(Multi-Mutation Adaptive Genetic Algorithm,MMAGA)[19],优化变量是单一代理模型的权系数ωk,目标函数是最小EOSM的预测误差,该优化问题表述如下:
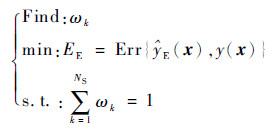
|
(11) |
式中:EE和Err{·}分别为EOSM的预测误差和误差测度,并采用均方根误差作为EOSM的误差测度;y(x)为x处的真实响应值。
1.7 代理模型预测精度的评价方法采用最大绝对误差(Maximum Absolute Error,MAE)、最大相对误差(Maximum Relative Error,MRE)和均方根误差(Root Mean Squared Error,RMSE)指标来衡量代理模型的预测精度,表达式分别为
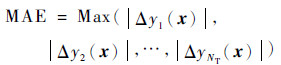
|
(12) |
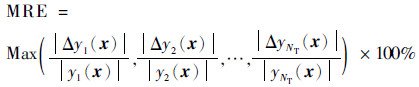
|
(13) |
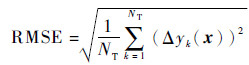
|
(14) |
式中: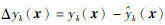
基于代理模型的制导火箭炮发射诸元计算流程如图 1所示,主要包括射角和无控弹道侧偏的代理模型构建、基于代理模型的发射诸元计算,其中射角和无控弹道侧偏的代理模型构建过程如下:

|
| 图 1 基于代理模型的制导火箭炮发射诸元计算流程 Fig. 1 Process for calculating firing data of guided rocket launcher based on surrogate model |
1) 建立弹道模型。弹道模型直接决定了发射诸元的计算精度。本文采用文献[20]中的六自由度弹道模型,该弹道模型综合考虑了地球自转及扁率的影响,并结合多次飞行试验结果进行了符合计算,运用该弹道模型得到的仿真结果与飞行试验结果高度吻合。
2) 运用代理模型建立射角、无控弹道侧偏与炮位纬度B0、炮位高程H0、射向AT、射程XG、目标点高程HT、药温TS之间的函数关系。具体过程包括数值试验设计得到试验数据、基于试验数据等进行代理模型的选择和拟合以及检验代理模型的预测精度等。
在给出炮位和目标点位置信息的情况下,制导火箭炮发射诸元的计算步骤如下:
1) 根据炮位和目标点的经度、纬度、高程,计算射程和射向。
2) 根据炮位纬度、炮位高程、射程、射向、目标点高程和药温,运用已经建立的无控弹道侧偏与各个影响因素之间的函数关系,计算无控弹道侧偏。
3) 根据射程和无控弹道侧偏,使用射向修正法计算射向修正量,从而得到修正的射向和射程。
4) 根据炮位纬度和高程、修正的射向和射程、目标点高程、药温,运用已经建立的射角与各个影响因素之间的函数关系,计算射角。
2.2 各试验点对应的射角和无控弹道侧偏的计算步骤各试验点对应的射角和无控弹道侧偏通过反复迭代六自由度弹道程序得到,计算步骤如下:
步骤1 运用二元三点插值法计算标准气象条件下给定的射程XG和炮位高程H0对应的射角θ1,并将θ1作为迭代计算的初值。
步骤2 使用六自由度弹道程序计算θ1对应的标准气象条件下的射程X1;并计算X1与XG的差值ΔX1 = XG-X1。
步骤3 根据ΔX1确定射角的迭代步长Δθ1,则第2次迭代的射角θ2 = θ1+Δθ1,并使用六自由度弹道程序计算θ2对应的射程X2。
步骤4 按照以下迭代修正公式确定更高精度的射角:
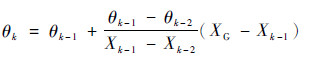
|
(15) |
式中:θk、θk-1和θk-2分别为迭代k、k-1和k-2次得到的射角;Xk-1和Xk-2分别为射角θk-1和θk-2对应的射程。基于式(15)进行射角的迭代计算,在每次迭代计算中使用六自由度弹道程序计算射角θk对应的射程Xk,直到|XG-Xk|满足给定的精度,并将试验点中的XG替换为Xk,同时输出射角θk对应的无控弹道侧偏。
在利用式(15)进行射角的迭代计算过程中,若射程XG大于给定的B0、H0、AT、HT、TS条件下的最大射程,则只需在式(15)的基础上,结合迭代关系式θk = θk-1+Δθk-1,将射角迭代到最大射程角,并输出最大射程角对应的射程和无控弹道侧偏,同时将试验点中的XG替换为最大射程。
2.3 射向修正法考虑到地球自转的影响,指向目标的远程火箭弹的无控弹道会存在一定的侧偏,且侧偏会随着射程和飞行时间的增加而增大。同时,由于远程火箭弹的气动舵较小,因而能提供的控制力有限。若按照传统的控制思路,在末制导段进行修正有可能导致该段长时间舵资源饱和,进而影响弹体稳定和落点精度。为了解决这一难题,提出了一种通过修正射向来减小侧偏的方法。
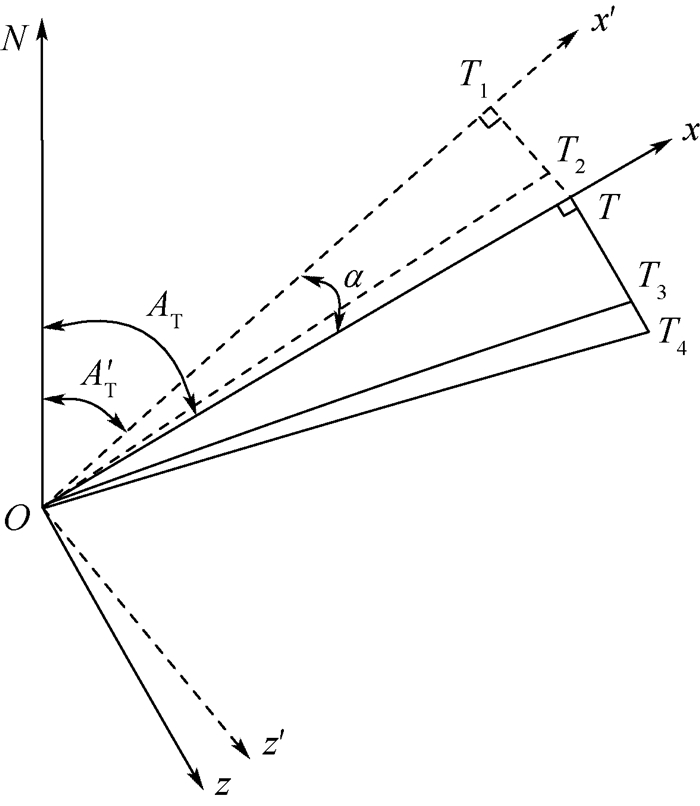
射向修正法的基本原理如图 2所示。其中O为炮位,T为真实目标点,T1为虚拟目标点,ON为真北轴,OT为真实射程,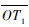
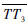
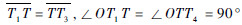
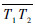
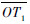
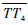
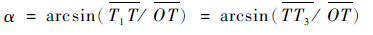
|
(16) |
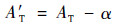
|
(17) |
|
| 图 2 射向修正法的原理示意图 Fig. 2 Schematic diagram of target azimuth correction method |
由图 2中的几何关系可知:

|
(18) |
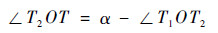
|
(19) |
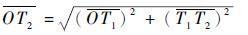
|
(20) |
通过射向修正法得到的无控弹道落点(T2)与真实目标点(T)之间的距离在地面坐标系下x轴和z轴方向的投影Δx和Δz分别满足如下关系:
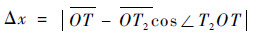
|
(21) |
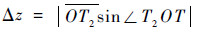
|
(22) |
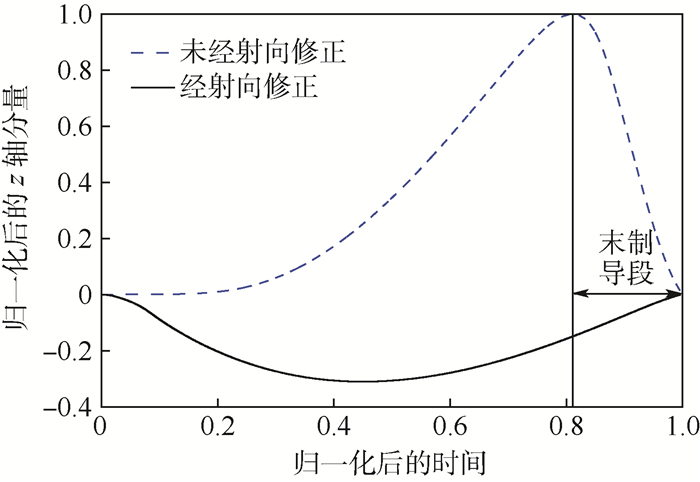
当制导火箭弹进入末制导段后,以某种导引方法将火箭弹导向目标。图 3给出了制导火箭弹在地面坐标系中的z轴分量随时间的变化关系。由图可知,经过射向修正可使得地面坐标系中的z轴分量在末制导段得到大幅度减小,从而可有效减小末制导段的舵资源压力。
|
| 图 3 制导火箭弹在地面坐标系中的z轴分量随时间的变化关系 Fig. 3 Variation of z-axis component of guided rocket in ground coordinate system with time |
基于国际标准大气(ISO 2533:1975[21]),分别运用PRS、Kriging、RBF、LSSVM、ELM和EOSM对射角和无控弹道侧偏进行了预测,并对各种代理模型的预测精度进行了比较分析。在此基础上,对射角和无控弹道侧偏进行了预测快速性分析,并对射向修正法的修正效果进行了分析。
本文采用LHS对各影响因素进行数值试验设计。各影响因素的取值范围如表 1所示,表中1 mil = 0.06°,训练样本数量为12 000,测试样本数量为5 000。
| 因素 | 范围 |
| B0/(°) | [0, 60.00] |
| H0/m | [0, 5 000.00] |
| AT/mil | [0, 6 000.00) |
| XG/km | [80.00,300.00] |
| HT/m | [0, 5 000.00] |
| TS/℃ | [-40.00, 50.00] |
3.1 代理模型的预测精度分析
表 2给出了不同阶数PRS的预测精度。对于射角和无控弹道侧偏的预测,在一定范围内,随着阶数的增加,PRS的预测精度会有所提高。对于常用的1~4阶PRS,其预测精度均较低,其中4阶PRS对应的射角、无控弹道侧偏的MAE和RMSE分别为6.167 mil和1.245 mil、509.76 m和94.03 m,主要由于低阶PRS仅适用于拟合一定复杂程度的函数关系,并可在局部范围内得到较精确的拟合效果,但当函数关系高度复杂时,低阶PRS的近似效果则较差。与低阶PRS相比,高阶PRS对射角和无控弹道侧偏的拟合效果均较好,其中9阶PRS的预测精度最高,对应的射角、无控弹道侧偏的MAE和RMSE分别为0.667 mil和0.084 mil、13.76 m和1.41 m,产生的射程MAE、MRE和RMSE分别为208.69m、0.13%和44.40 m。因此,9阶PRS可更好地用于建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的高度非线性函数关系。
| 阶数 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| 1 | 50.867 | 5.023 | 11.813 | 2455.38 | 606.87 | 17422.75 | 11.57 | 6658.22 | ||
| 2 | 24.550 | 3.211 | 7.545 | 1485.90 | 347.41 | 11483.88 | 8.50 | 4 490.55 | ||
| 3 | 9.817 | 1.236 | 2.385 | 914.41 | 185.51 | 4331.12 | 2.97 | 1368.86 | ||
| 4 | 6.167 | 0.652 | 1.245 | 509.76 | 94.03 | 2830.85 | 1.25 | 706.48 | ||
| 5 | 3.737 | 0.384 | 0.590 | 234.81 | 37.76 | 1298.65 | 0.77 | 320.38 | ||
| 6 | 2.333 | 0.240 | 0.323 | 99.02 | 16.15 | 768.27 | 0.47 | 172.21 | ||
| 7 | 1.476 | 0.151 | 0.186 | 49.15 | 7.01 | 519.29 | 0.23 | 95.82 | ||
| 8 | 1.085 | 0.111 | 0.120 | 25.06 | 3.46 | 343.80 | 0.15 | 61.56 | ||
| 9 | 0.667 | 0.068 | 0.084 | 13.76 | 1.41 | 208.69 | 0.13 | 44.40 | ||
| 10 | 0.792 | 0.078 | 0.088 | 18.10 | 1.93 | 245.16 | 0.14 | 46.51 | ||
表 3给出了回归模型为6阶多项式的条件下,8种相关函数对Kriging预测精度的影响。对于射角和无控弹道侧偏的预测,Kriging具有较高的精度,且在各样本点处的预测值与真实值相同。相关函数对Kriging的预测精度会有很大影响,相关函数为Gauss函数和Spline函数时,Kriging具有很高的预测精度,而相关函数为Lin函数和Exp函数时,Kriging的预测精度则较低,其中相关函数为Gauss函数的Kriging对应的射角、无控弹道侧偏的MAE和RMSE分别为0.483 mil和0.064 mil、6.64 m和0.65 m,产生的射程MAE、MRE和RMSE分别为182.31 m、0.09%和33.45 m。因此,运用Kriging建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的函数关系时,优先选择的相关函数为Gauss函数。
| 相关函数 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| Cubic | 0.550 | 0.068 | 0.079 | 14.26 | 1.50 | 217.88 | 0.11 | 45.18 | ||
| Exp | 1.667 | 0.176 | 0.168 | 64.60 | 6.52 | 583.94 | 0.23 | 69.05 | ||
| Gauss | 0.483 | 0.051 | 0.064 | 6.64 | 0.65 | 182.31 | 0.09 | 33.45 | ||
| Lin | 1.567 | 0.164 | 0.174 | 65.82 | 5.84 | 564.56 | 0.22 | 76.00 | ||
| Matern32 | 1.433 | 0.151 | 0.117 | 34.79 | 2.44 | 542.97 | 0.21 | 51.70 | ||
| Matern52 | 1.183 | 0.124 | 0.099 | 16.82 | 1.25 | 449.70 | 0.17 | 48.59 | ||
| Spherical | 1.583 | 0.167 | 0.165 | 58.83 | 5.55 | 602.85 | 0.24 | 67.90 | ||
| Spline | 0.533 | 0.056 | 0.070 | 10.68 | 1.08 | 201.42 | 0.10 | 40.79 | ||
5种基函数对RBF预测精度的影响如表 4所示。对于射角和无控弹道侧偏的预测,基函数的类型对RBF的预测精度影响较大,当基函数为MN函数和TPS函数以及IMQ函数和MQ函数时,RBF的预测精度均较为接近,其中MN函数的阶数为最佳阶数11。当基函数采用11阶MN函数和Gauss函数时,RBF分别具有最好和最差的预测效果,其中基函数为11阶MN函数的RBF对应的射角、无控弹道侧偏的MAE和RMSE分别为1.033 mil和0.133 mil、23.22 m和2.59 m,产生的射程MAE、MRE和RMSE分别为414.72 m、0.25%和69.86 m。因此,运用RBF建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的函数关系时,最优基函数为11阶MN函数。
| 基函数 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| Gauss | 1.783 | 0.189 | 0.240 | 26.05 | 2.88 | 852.03 | 0.51 | 131.14 | ||
| IMQ | 1.350 | 0.165 | 0.182 | 23.69 | 2.64 | 680.56 | 0.53 | 101.25 | ||
| MN | 1.033 | 0.105 | 0.133 | 23.22 | 2.59 | 414.72 | 0.25 | 69.86 | ||
| MQ | 1.317 | 0.158 | 0.179 | 24.30 | 2.67 | 657.65 | 0.50 | 98.90 | ||
| TPS | 1.103 | 0.117 | 0.139 | 23.44 | 2.66 | 443.64 | 0.34 | 74.68 | ||
3种核函数对LSSVM预测精度的影响如表 5所示。核函数的选取对LSSVM的预测效果有较大影响。当核函数采用Gauss函数和8阶Polynomial函数时,LSSVM的射角和无控弹道侧偏预测结果精度均较好,且核函数为Gauss函数的LSSVM具有更高的预测精度,其对应的射角、无控弹道侧偏的MAE和RMSE分别为0.983 mil和0.114 mil、13.85 m和1.77 m,产生的射程MAE、MRE和RMSE分别为335.83 m、0.16%和57.17 m;而当核函数采用Lin函数时,LSSVM的射角和无控弹道侧偏预测效果精度很差。因此,运用LSSVM建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的函数关系时,可以选择的核函数为Gauss函数和高阶Polynomial函数,但优先选择Gauss函数。
| 核函数 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| Lin | 50.850 | 5.020 | 11.813 | 2455.39 | 606.87 | 17422.75 | 11.56 | 6658.22 | ||
| Polynomial | 1.017 | 0.106 | 0.120 | 24.49 | 3.50 | 365.25 | 0.17 | 61.98 | ||
| Gauss | 0.983 | 0.102 | 0.114 | 13.85 | 1.77 | 335.83 | 0.16 | 57.17 | ||
表 6给出了5种激活函数对ELM预测精度的影响。激活函数的选取对ELM的预测效果有较大影响。对于射角和无控弹道侧偏的预测,当激活函数分别采用Sine函数和Tribas函数时,ELM具有最好和最差的预测效果,其中激活函数为Sine函数的ELM对应的射角、无控弹道侧偏的MAE和RMSE分别为1.117 mil和0.130 mil、24.18 m和2.65 m,产生的射程MAE、MRE和RMSE分别为337.00 m、0.22%和66.95 m。因此,运用ELM建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的函数关系时,最优激活函数为Sine函数。
| 激活函数 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| Radbas | 11.850 | 1.932 | 1.202 | 190.80 | 17.04 | 6 131.68 | 4.78 | 762.77 | ||
| Sigmoid | 1.167 | 0.135 | 0.157 | 33.68 | 3.15 | 640.92 | 0.44 | 85.99 | ||
| Sine | 1.117 | 0.115 | 0.130 | 24.18 | 2.65 | 337.00 | 0.22 | 66.95 | ||
| Tanh | 8.350 | 1.412 | 0.920 | 160.13 | 15.40 | 5692.56 | 3.86 | 581.62 | ||
| Tribas | 59.217 | 8.505 | 9.667 | 2 468.48 | 519.41 | 41920.08 | 31.48 | 6278.87 | ||
选择高阶PRS(PRSho,阶数为9)、相关函数为Gauss函数的Kriging(KRIGg)、基函数为MN函数的RBF(RBFm,阶数为11)、核函数为Gauss函数的LSSVM(LSSVMg)和激活函数为Sine函数的ELM(ELMs)构建组合代理模型,设置MMAGA算法的参数为:种群大小NP = 80,最大进化代数NG = 300,杂交常数Pc1 = 0.62,杂交常数Pc2 = 0.88,变异常数Pm1 = 0.02,变异常数Pm2 = 0.05。对于射角的EOSM,PRSho、KRIGg、RBFm、LSSVMg和ELMs的权系数依次为0.146 140、0.775 976、0.016 503、0.044 457和0.016 924;对于无控弹道侧偏的EOSM,PRSho、KRIGg、RBFm、LSSVMg和ELMs的权系数依次为0.117 428、0.825 656、0.011 516、0.034 321和0.011 079。
表 7给出了各种代理模型的预测精度。6种代理模型对射角的预测精度从高到低依次为EOSM、KRIGg、PRSho、LSSVMg、ELMs、RBFm,对无控弹道侧偏的预测精度从高到低依次为EOSM、KRIGg、PRSho、LSSVMg、RBFm、ELMs,其中EOSM和KRIGg以及ELMs和RBFm对射角和无控弹道侧偏的预测精度均较为接近,且EOSM和KRIGg的预测精度明显高于ELMs和RBFm的预测精度。与单一代理模型相比,EOSM对射角和无控弹道侧偏的预测精度并没有显著提高,其主要原因是:KRIGg的预测精度明显高于其他的单一代理模型,其对应的权系数也最大,EOSM的预测精度在很大程度上取决于KRIGg的预测精度。因此,在运用代理模型建立射角、无控弹道侧偏与B0、H0、AT、XG、HT、TS之间的函数关系时,优先选择的单一代理模型为KRIGg。
| 模型类型 | 射角 | 无控弹道侧偏 | 射程 | |||||||
| MAE/mil | MRE/% | RMSE/mil | MAE/m | RMSE/m | MAE/m | MRE/% | RMSE/m | |||
| PRSho | 0.667 | 0.068 | 0.084 | 13.76 | 1.41 | 208.69 | 0.13 | 44.40 | ||
| KRIGg | 0.483 | 0.051 | 0.064 | 6.64 | 0.65 | 182.31 | 0.09 | 33.45 | ||
| RBFm | 1.033 | 0.105 | 0.133 | 23.22 | 2.59 | 414.72 | 0.25 | 69.86 | ||
| LSSVMg | 0.983 | 0.102 | 0.114 | 13.85 | 1.77 | 335.83 | 0.16 | 57.17 | ||
| ELMs | 1.117 | 0.115 | 0.130 | 24.18 | 2.65 | 337.00 | 0.22 | 66.95 | ||
| EOSM | 0.467 | 0.049 | 0.061 | 5.93 | 0.60 | 177.69 | 0.08 | 32.60 | ||
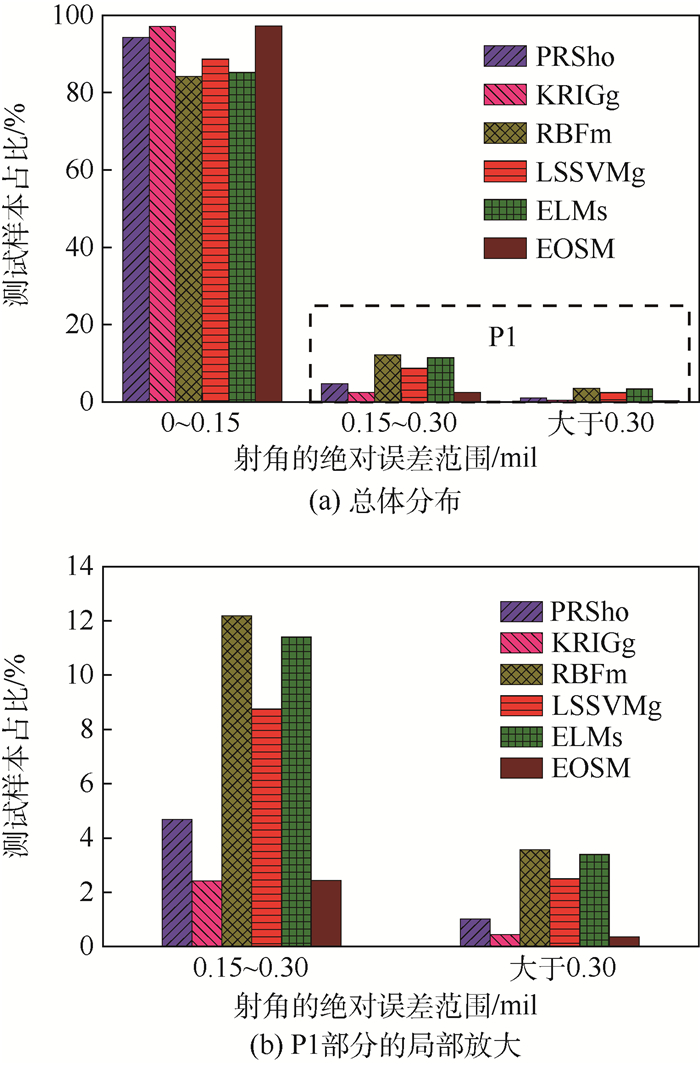
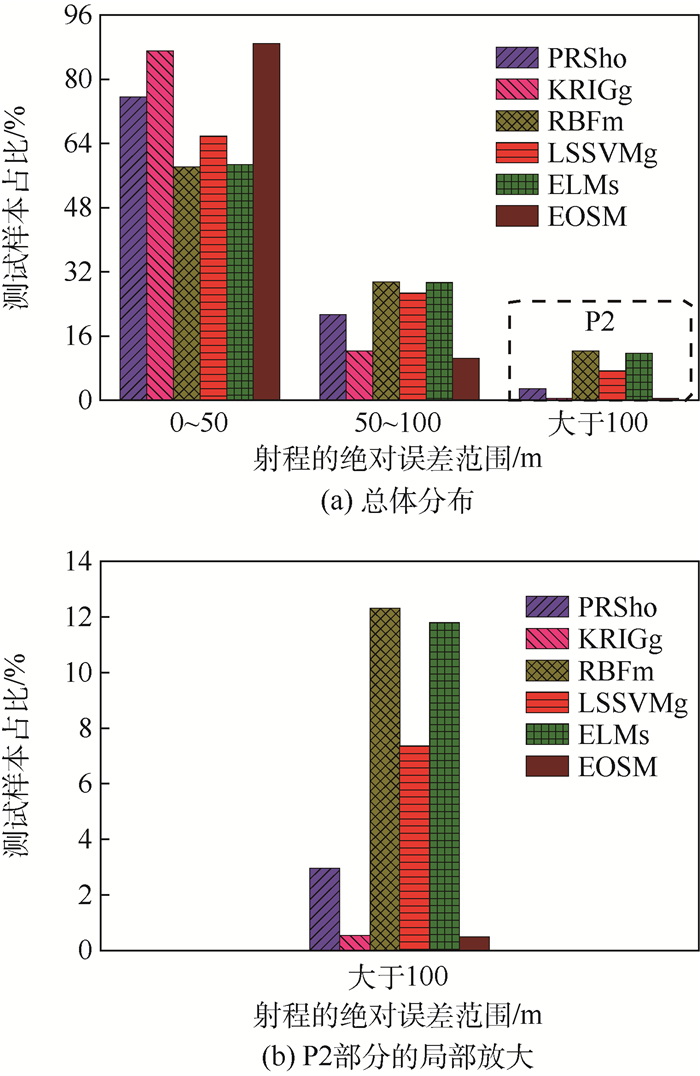
图 4和图 5给出了6种代理模型对应的射角和射程的绝对误差分布情况。由图 4可知,在5 000个测试样本中,6种代理模型对应的射角绝对误差小于0.15 mil的测试样本占比均达84.24%以上,小于0.30 mil的测试样本占比均达96.42%以上,其中EOSM、KRIGg、PRSho对应的射角绝对误差小于0.15 mil和0.30 mil的测试样本占比均分别达94.30%以上和98.98%以上。由于射角的预测误差产生的射程误差的分布情况如图 5所示,6种代理模型对应的射程绝对误差小于50 m的测试样本占比均达58.22%以上,小于100 m的测试样本占比均达87.68%以上,其中EOSM、KRIGg、PRSho对应的射程绝对误差小于50 m和100 m的测试样本占比均分别达75.62%以上和97.04%以上。分析结果进一步验证了基于代理模型的射角预测方法具有很高的精度。
|
| 图 4 射角的绝对误差分布情况 Fig. 4 Distribution of absolute error of firing angle |
|
| 图 5 射程的绝对误差分布情况 Fig. 5 Distribution of absolute error of range |
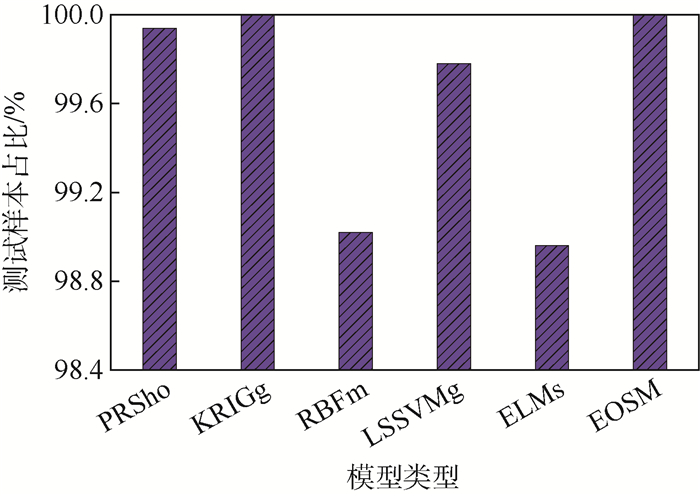
图 6给出了6种代理模型对应的无控弹道侧偏绝对误差小于10 m的测试样本占比。在5 000个测试样本中,6种代理模型对应的无控弹道侧偏绝对误差小于10 m的测试样本占比均达98.96%以上,其中EOSM、KRIGg和PRSho对应的测试样本占比均达99.94%以上。分析结果进一步验证了基于代理模型的无控弹道侧偏预测方法具有很高的精度。
|
| 图 6 无控弹道侧偏的绝对误差小于10 m的测试样本占比 Fig. 6 Percentage of testing samples with absolute error of uncontrolled lateral range less than 10 m |
基于已建立的各种代理模型,使用Microsoft Visual C++ 6.0编写了射角和无控弹道侧偏的预测程序,程序运行的软硬件环境为:CPU为Intel(R)Core(TM) i5-6300HQ 2.30 GHz,内存空间为4.00 GB,操作系统为Windows7 64位。以5 000个测试样本为例,统计6种代理模型运行一次射角和无控弹道侧偏预测程序所需要的平均时间。对于同一种代理模型,射角预测程序的运行时间与无控弹道侧偏预测程序的运行时间非常接近,因此本文仅给出了6种代理模型的射角预测程序的运行时间,如图 7所示。5种单一代理模型预测射角需要的时间均小于1 ms,其中预报速度最快和最慢的分别是PRSho和KRIGg,预测时间分别为0.036 8 ms和0.948 5 ms。运用组合代理模型预测射角需要的时间为3.340 9 ms。在极短的时间内,运用各种代理模型即可获得精度较高的射角和无控弹道侧偏。

|
| 图 7 各种代理模型运行一次射角预测程序所需要的时间 Fig. 7 Execution time of various surrogate models for running one-time firing angle prediction program |
运用5 000个测试样本对射向修正法的修正效果进行了验证,如表 8所示,表中,(Δz)Max和(Δx)Max分别表示5 000个测试样本中Δz和Δx的最大值,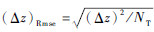
| m | |||
| 模型类型 | (Δ z)Max | (Δ z)Rmse | (Δ x)Max |
| PRSho | 24.19 | 4.62 | 0.42 |
| KRIGg | 23.75 | 4.49 | 0.42 |
| RBFm | 28.72 | 5.05 | 0.50 |
| LSSVMg | 25.82 | 4.71 | 0.43 |
| ELMs | 33.13 | 5.18 | 0.48 |
| EOSM | 23.51 | 4.46 | 0.41 |
3.4 样本数量对预测精度的影响分析
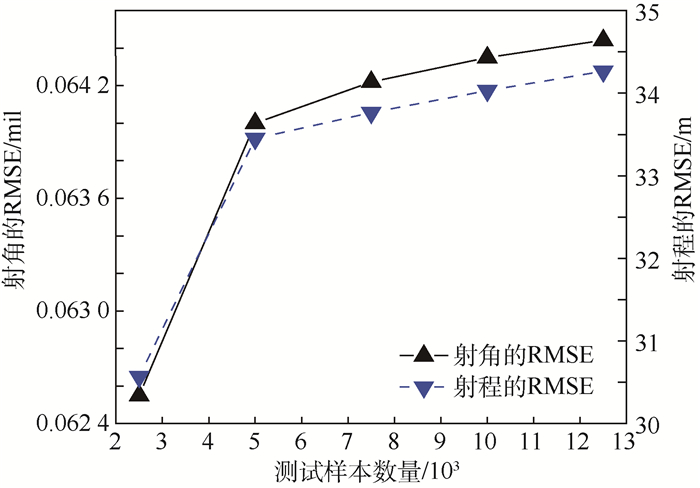
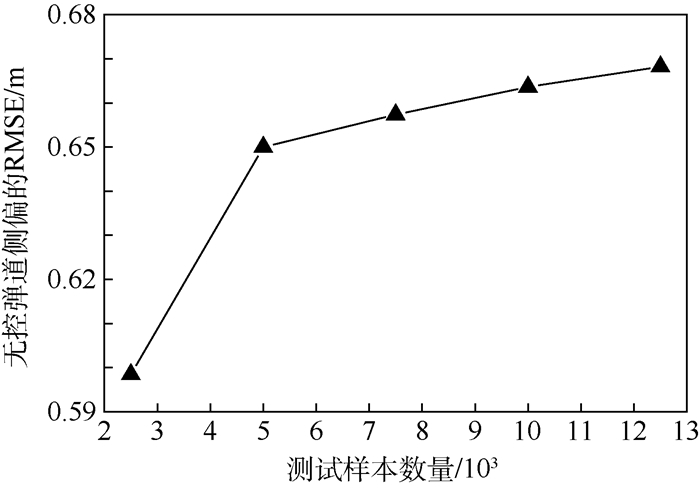
图 8和图 9给出了代理模型为KRIGg和训练样本数量为12 000的情况下测试样本数量对射角和无控弹道侧偏的预测精度影响。随着测试样本数量的增加,射角和无控弹道侧偏的RMSE均增加,当测试样本数量超过5 000时,二者增加的速度明显减缓,测试样本数量对其他代理模型的预测精度影响类似。因此,5 000个测试样本即能够很好地反映出各种代理模型的预测精度。
|
| 图 8 KRIGg对射角的预测精度随测试样本数量的变化 Fig. 8 Variation of KRIGg prediction accuracy of firing angle with testing sample size |
|
| 图 9 KRIGg对无控弹道侧偏的预测精度随测试样本数量的变化 Fig. 9 Variation of KRIGg prediction accuracy of uncontrolled lateral range with testing sample size |
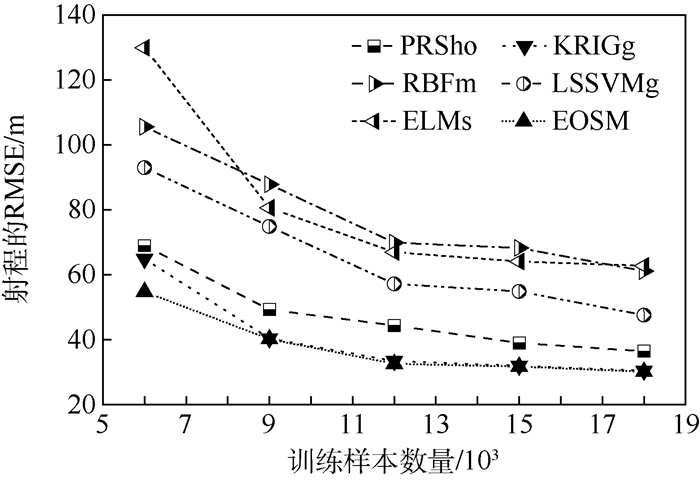
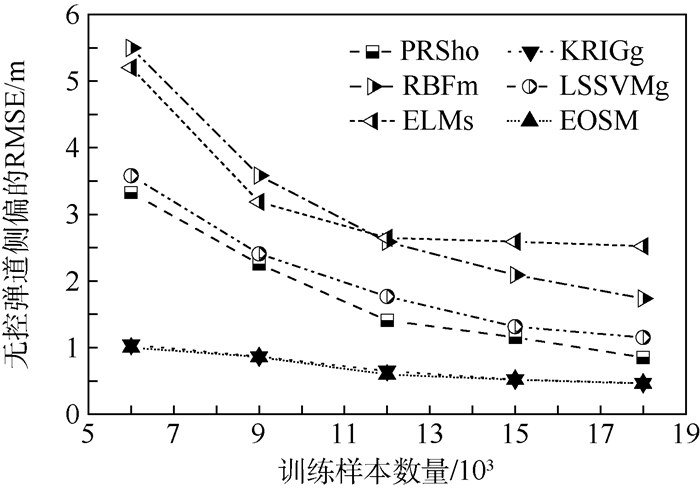
图 10~图 12给出了测试样本数量为5 000的情况下训练样本数量对射角和无控弹道侧偏的预测精度影响,其中训练样本6 000、9 000、15 000和18 000对应的PRSho最佳阶数依次为8、9、10和10,对应的RBFm最佳阶数依次为9、11、13和13。对于同一种代理模型,随着训练样本数量的增加,射角和无控弹道侧偏的RMSE均显著减小,表明代理模型对射角和无控弹道侧偏的预测精度随着训练样本数量的增加而得到显著提高;当训练样本数量超过12 000时,二者的减小速度明显减缓,射程的RMSE随训练样本数量的变化规律与射角的RMSE随训练样本数量的变化规律相同。因此,12 000个训练样本即能够很好地反映出各种代理模型的预测精度。此外,与RBFm和ELMs相比,PRSho、KRIGg、LSSVMg和EOSM对射角和无控弹道侧偏的预测精度均更高。

|
| 图 10 射角的预测精度随训练样本数量的变化 Fig. 10 Variation of prediction accuracy of firing angle with training sample size |
|
| 图 11 由射角的预测误差引起的射程误差随训练样本数量的变化 Fig. 11 Variation of range error due to prediction error of firing angle with training sample size |
|
| 图 12 无控弹道侧偏的预测精度随训练样本数量的变化 Fig. 12 Variation of prediction accuracy of uncontrolled lateral range with training sample size |
基于大样本数据,运用多种代理模型建立了射角、无控弹道侧偏与各个影响因素之间的函数关系,有效解决了制导火箭炮发射诸元的快速计算问题,主要结论如下:
1) PRSho、KRIGg、RBFm、LSSVMg、ELMs和EOSM可更好地用于建立射角、无控弹道侧偏与各个影响因素之间的函数关系。与RBFm和ELMs相比,PRSho、KRIGg、LSSVMg和EOSM对射角和无控弹道侧偏的预测精度均更高,4种代理模型的预测精度从高到低依次为EOSM、KRIGg、PRSho、LSSVMg。
2) 基于代理模型的射角和无控弹道侧偏预测方法具有精度高、速度快等优点,该方法可为制导火箭炮发射诸元的计算提供一种新的解决方案。
3) 射向修正法可以有效减小由于地球自转引起的无控弹道侧偏,从而可以有效减小制导火箭弹末制导段的舵资源压力。
随着人工智能和机器学习等技术的快速发展,制导火箭炮发射诸元计算方法的研究和应用也会获得长足发展。
| [1] |
杨明, 高宏伟, 汤祁忠. 制导火箭弹射表编拟研究[J]. 火力与指挥控制, 2013, 38(12): 156-159. YANG M, GAO H W, TANG Q Z. Research on compilation of firing tables of guided rocket[J]. Fire Control & Command Control, 2013, 38(12): 156-159. DOI:10.3969/j.issn.1002-0640.2013.12.041 (in Chinese) |
| [2] |
徐劲祥, 祁载康, 林德福, 等. 火箭炮射表编拟及发射诸元快速装定研究[J]. 南京理工大学学报, 2004, 28(3): 333-336. XU J X, QI Z K, LIN D F, et al. Study on the compilation of firing tables and rapid firing elements binding of rocket gun system[J]. Journal of Nanjing University of Science and Technology, 2004, 28(3): 333-336. DOI:10.3969/j.issn.1005-9830.2004.03.026 (in Chinese) |
| [3] |
韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2014: 467-472. HAN Z P. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press, 2014: 467-472. (in Chinese) |
| [4] |
CHUSILP P, CHARUBHUN W, RIDLUAN A.Developing firing table software for artillery projectiles using iterative search and 6-DOF trajectory model[C]//Proceedings of the Second TSME International Conference on Mechanical Engineering.Krabi: The Thai Society of Mechanical Engineers, 2011: AME04.
|
| [5] |
周珞晶, 张为华, 苏明照, 等. 火箭弹计算机射表的发射角快速确定方法[J]. 弹箭与制导学报, 1998(4): 48-52. ZHOU L J, ZHANG W H, SU M Z, et al. Rapid determining method for launching angle of computer's firing table of rocket projectiles[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 1998(4): 48-52. (in Chinese) |
| [6] |
赵东华, 张怀智, 郭胜强, 等. 基于二分法的弹道解算决定火炮射击诸元[J]. 火力与指挥控制, 2012, 37(12): 182-183. ZHAO D H, ZHANG H Z, GUO S Q, et al. Researched on determining firing data of gun based on solving ballistic equations with binary search[J]. Fire Control & Command Control, 2012, 37(12): 182-183. DOI:10.3969/j.issn.1002-0640.2012.12.048 (in Chinese) |
| [7] |
CHUSILP P, CHARUBHUN W, NUTKUMHANG N.Investigating an iterative method to compute firing angles for artillery projectiles[C]//Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Piscataway, NJ: IEEE Press, 2012: 940-945.
|
| [8] |
CHARUBHUN W, CHUSILP P.Development of automatic firing angle calculation for ground to ground MLRS[C]//Proceedings of the 2015 Asian Conference on Defence Technology. Piscataway, NJ: IEEE Press, 2015: 17-26.
|
| [9] |
VIANA F A C, SIMPSON T W, BALABANOV V, et al. Metamodeling in multidisciplinary design optimization:How far have we really come?[J]. AIAA Journal, 2014, 52(4): 670-690. DOI:10.2514/1.J052375 |
| [10] |
KOZIEL S, LEIFSSON L. Surrogate-based modeling and optimization[M]. Berlin: Springer, 2013: 285-391.
|
| [11] |
VIANA F A C.Surrogates toolbox user's guide version 3.0[EB/OL].[2018-06-06]. http://sites.google.com/site/felipe-acviana/surrogatestoolbox.
|
| [12] |
FORRESTER A I J, SOBESTER A, KEANE A J.Engineering design via surrogate modelling: A practical guide[M].West Sussex: John Wiley & Sons Ltd., 2008: 49-63.
|
| [13] |
陈文, 傅卓佳, 魏星. 科学与工程计算中的径向基函数方法[M]. 北京: 科学出版社, 2014: 28-33. CHEN W, FU Z J, WEI X. Radial basis function methods in science and engineering calculation[M]. Beijing: Science Press, 2014: 28-33. (in Chinese) |
| [14] |
SUYKENS J A K, GESTEL T V, BRABANTER J D, et al. Least squares support vector machines[M]. Hackensack, NJ: World Scientific, 2002: 71-116.
|
| [15] |
HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]//Proceedings of the 2004 IEEE International Joint Conference on Neural Networks. Piscataway, NJ: IEEE Press, 2004: 985-990.
|
| [16] |
RASMUSSEN C E, WILLIAMS C K I. Gaussian process for machine learning[M]. Cambridge: Massachusetts Institute of Technology Press, 2006: 85.
|
| [17] |
CRISTIANINI N, SHAWE-TAYLOR J. An introduction to support vector machines and other kernel-based learning methods[M]. Cambridge: Cambridge University Press, 2000: 112.
|
| [18] |
马洋, 罗文彩.组合代理模型研究及在飞行器气动性能预测中的应用[C]//第17届中国系统仿真技术及其应用学术年会论文集.北京: 中国自动化学会系统仿真专业委员会, 2016: 26-31. MA Y, LUO W C. Study on ensemble of surrogate models and application in prediction of aerodynamic characteristics of space vehicle[C]//Proceedings of 17th Chinese Conference on System Simulation Technology & Application. Beijing: System Simulation Committee of Chinese Association of Automation, 2016: 26-31(in Chinese). |
| [19] |
龚纯, 王正林. 精通MATLAB最优化计算[M]. 3版. 北京: 电子工业出版社, 2014: 337-341. GONG C, WANG Z L. Proficient in MATLAB optimization calculation[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2014: 337-341. (in Chinese) |
| [20] |
张志勇, 陈志华, 黄振贵, 等.远程火箭弹精度影响分析及其修正[C]//中国力学大会-2015论文摘要集.北京: 中国力学学会办公室, 2015: 239. ZHANG Z Y, CHEN Z H, HUANG Z G, et al. Precision influence analysis and modification of long-range rockets[C]//Collection of Extent Abstracts of the Chinese Congress of Theoretical and Applied Mechanics 2015.Beijing: Chinese Society of Theoretical and Applied Mechanics Office, 2015: 239(in Chinese). |
| [21] |
International Organization for Standardization (ISO). Standard atmosphere: ISO 2533: 1975[S].Geneva: ISO, 1975.
|



