2. 西北工业大学 航空学院, 西安 710072
2. College of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
灵敏度分析方法主要研究结构系统的输入变量对输出响应的影响程度[1],已广泛应用于可靠性工程[2]、危险分析[3-4]、环境科学[5]、计算物理化学[6-7]等领域。灵敏度分析一般分为局部灵敏度分析方法和全局灵敏度分析方法。局部灵敏度分析方法研究模型输入变量的分布参数对结构系统输出响应的影响程度[8],只能反映输入变量在某一名义值处对输出响应的影响,具有很大的局限性[9]。
全局灵敏度分析,也称为重要性测度分析,研究一个或多个输入变量对模型输出响应的影响程度,能够反映输入变量对结构系统输出响应的平均影响程度,因此,该分析方法在实际工程中得到了更广泛的应用。重要性测度分析方法的核心思想是对影响结构系统输出响应的输入变量进行重要性排序,从而得到对结构系统输出响应影响较大的输入变量,为结构系统的设计改进提供理论依据。近年来,研究人员已经提出了很多重要性测度分析方法。Saltelli和Helton提出了无参的方法,但缺乏模型的独立性[9-10]。Sobol[11]和Iman[12]等提出了基于方差的重要性测度分析方法和相应的求解算法,该方法隐含地假设了方差可以充分描述结构系统输出响应的不确定性。然而,相关学者指出随机变量的任何一阶矩只能反映其部分信息,必然会丢失一些信息[13]。为了分析输入变量在其整个分布区域上对结构系统输出响应的影响程度,Borgonovo[14]、Liu[15]和Li[16]等又分别提出了矩独立重要性测度分析(Moment-independent Importance Measures analysis,M-IM)方法。
目前,Borgonovo[14]所提出的矩独立重要性测度分析方法应用最为广泛。但在可靠性分析中,结构系统的失效概率通常是工程技术人员所关注的焦点。Li等[16]又提出了基于失效概率的矩独立重要性测度分析方法,该方法能够计算输入变量在其分布区域的任一固定点时,结构系统的无条件失效概率和条件失效概率的平均偏差。然而,在实际工程中将输入变量固定于某一点,这是很难实现的,只能使输入变量在其分布区域的某一区间上缩减变化。
为了解决这一问题,Wei等[17]提出了一种新的输入变量缩减区间的获取方法,该方法的基本思想是:首先产生2个随机数q1和q2,q1和q2服从均匀分布,q1~U(0, 1),q2~U(q1, 1),然后根据输入变量累积分布函数的逆函数F-1(·),得到输入变量的缩减区间[F-1(q1), F-1(q2)]。该方法的优点是很容易获取输入变量的缩减区间,然而它并没有考虑输入变量缩减区间获取的任意性和等可能性。
本文提出了一种新的基于失效概率的矩独立重要性测度分析方法,并给出了一种更加合理的输入变量缩减区间的获取方法。同时,引入自适应超球重要抽样(Adaptive Radial-Based Importance Sampling,ARBIS)方法[18-19],构建所提新指标的高效求解算法。应用数值算例和工程算例,验证本文所提新指标的合理性和求解算法的高效性。
1 新的矩独立重要性测度指标 1.1 新指标的定义假设结构系统的极限状态函数为Y=g(X),X为n维输入变量,即X=(X1, X2, …, Xn)。记输入变量Xi的基于失效概率的矩独立重要性测度指标为δiP,可以表示为
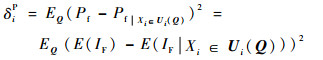
|
(1) |
式中:Pf为非条件失效概率;Q为分位数矩阵,用来生成输入变量Xi的缩减区间;当Xi的分布区间缩减到其所有可能的子区间Ui(Q)时,就能够得到条件失效概率Pf|Xi∈Ui(Q);EQ(·)为对Q求期望;IF为指示函数,当X位于失效域(即g(X)≤0)时,IF(x)=1,否则IF(x)=0。
在式(1)中,基于失效概率的矩独立重要性测度指标δiP表示了当输入变量Xi在其分布区域的所有可能缩减区间上变化时,对结构系统失效概率的平均影响程度。
1.2 输入变量缩减区间获取方法为了等概率地获取输入变量所有可能的缩减区间,首先定义一个分位数矩阵Hk(3×2):

|
(2) |
式中:hk(1)和hk(2)为[0, 1]区间上的2个随机数,满足0≤hk(1)<hk(2)≤1(k=1, 2, …, N)。
Hk(k=1, 2, …, N)组成一个(3N×2)的分位数矩阵Q:

|
(3) |
式中:Hk(k=1, 2, …, N)是被等概率获取的,例如P{Hk}=1/N。
为了更好地理解式(3),可表示为

|
(4) |
式中:q3k-2(1)=0,q3k-2(2)=q3k-1(1)=hk(1),q3k-1(2)=q3k(1)=hk(2),q3k(2)=1 (k=1, 2, …, N)。
因此,根据分位数矩阵Q就可以定义缩减区间矩阵U为
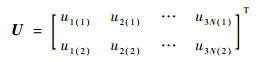
|
(5) |
式中:uj(1)=FX-1(qj(1)),uj(2)=FX-1(qj(2)),j=1, 2, …, 3N;FX-1(·)为输入变量X的累积分布函数的逆函数。通过获取(uj(1), uj(2))(j=1, 2, …, 3N),输入变量X所有可能的缩减区间就能够被等可能地取得。
对于输入变量Xi,其缩减区间可表示为
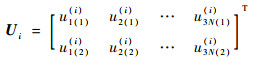
|
(6) |
式中:uj(1)(i)=FXi-1(qj(1)),uj(2)(i)=FXi-1(qj(2)),j=1, 2, …, 3N, FXi-1(·)为输入变量Xi的累积分布函数的逆函数, Xi∈[uj(1)(i), uj(2)(i)] (j=1, 2, …, 3N)为输入变量Xi的第j个缩减区间。
上述是一种新的区间划分技术来获取输入变量在其分布区域上所有可能的缩减区间。本文所提出的这种新的区间获取方法具有2个优点:①输入变量所有可能的缩减区间能够被等可能地获取,从而就能够更加合理地计算当输入变量在其分布区域的缩减区间上变化时对结构系统失效概率的平均影响程度;②全期望公式在这种区间划分技术中成立,基于全期望公式,第2节中就能够将本文提出的新的基于失效概率的矩独立重要性测度指标转化为更加便于计算的基于方差的重要性测度指标。
2 新指标与基于方差的指标的关系由于1.2节中提出的输入变量缩减区间获取方法中全期望公式成立,就能够推导出新的矩独立重要性测度指标与基于方差的重要性测度指标间的关系,同时得到一种新的基于方差的矩独立重要性测度指标表示方式。
输入变量在缩减区间上的全期望公式表示为
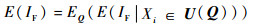
|
(7) |
证明过程详见附录A。
因此,本文所提出的新的基于失效概率的矩独立重要性测度指标δiP可表示

|
(8) |
从式(8)中可以看出,新的矩独立重要性测度指标能够很容易地转换为基于方差的重要性测度指标,从而新的矩独立重要性测度指标就能够采用基于方差的重要性测度分析方法来进行求解。
3 新指标的高效求解算法新的矩独立重要性测度指标传统的计算方法是双层重复抽样蒙特卡罗(Double-Loop-Repeat-Set Monte Carlo,DLRS MC)[17]方法,该方法先用N个样本点计算非条件失效概率,然后在每一个子区间上,再产生N个新的样本点来计算条件失效概率,最后计算非条件失效概率和条件失效概率差异的平均值。
DLRS MC方法可以获得高精度的结果值,但其计算量很大,计算效率较低。本节提出了一种新的求解算法——ARBIS方法,旨在对新的矩独立重要性测度指标进行高效求解。
3.1 自适应超球重要抽样方法ARBIS方法最初是用来计算失效概率的,而计算新的基于失效概率的矩独立重要性测度指标的核心就是计算非条件失效概率和条件失效概率。因此,本节基于ARBIS方法构建新指标的求解算法。
ARBIS方法[18-19]的基本思想是自适应地寻找到一个落在功能函数安全域内的最大的超球。当抽样点落入超球内部时,就将该抽样点归类为安全点,不必再代入结构系统功能函数进行求解。因此,该方法在计算结构系统输出响应的失效概率时,计算量将大幅度降低。同时,ARBIS方法采用自适应的方法来获取满足条件的最大超球半径,相比于传统的梯度搜索算法,效率更高,稳健性也更好。
任何一个随机变量通过合适的变换方法,都可以转换到标准正态空间中[20-21]。因此,以下步骤都假定在标准正态空间中进行。为了更好地理解ARBIS方法,给出该方法的一些关键步骤。
步骤1 设定初始化超球半径β0。为了确保超球与失效域相交,初始半径β0可通过式(9)来确定:
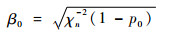
|
(9) |
式中:χn-2表示卡方分布χn2的累积分布函数的逆函数;p0为抽样点落在超球外部的概率,一般取很小值来确保初始超球与失效域相交。
步骤2 根据随机变量的分布类型,通过转化得到标准正态空间的样本点uk(k=1, 2, …, N)。
步骤3 计算落在半径为β0的超球外部样本点的极限状态函数值,确定失效样本点。如果样本点满足‖uk‖≥β0,计算其极限状态函数值并保存结果。同时,对于满足极限状态函数值g(uk)≤0的样本点,如果总数目为Nf,按照式(10)进行失效概率值的累加计算:

|
(10) |
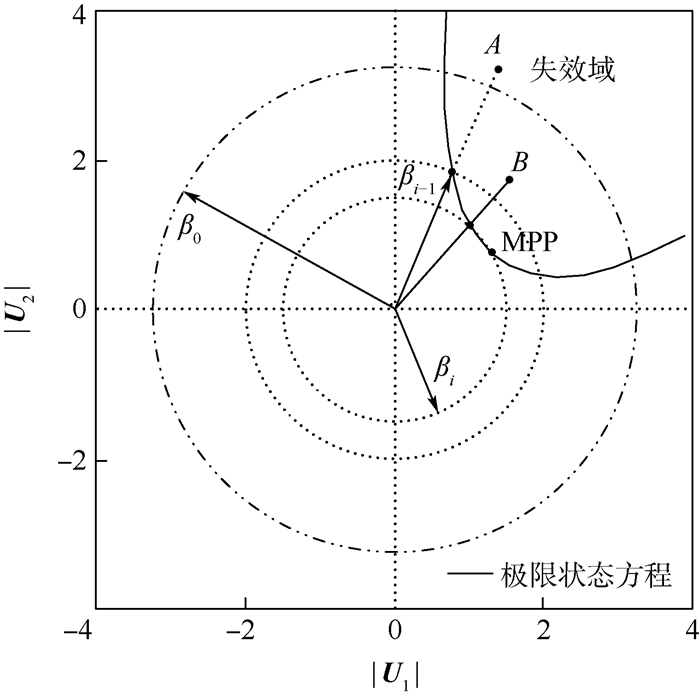
步骤4 确定第i次迭代的超球半径βi。如果抽样点满足g(uk)≤0且‖uk‖>βi-1,则其为落在第i-1次迭代超球外的失效样本点,如图 1中所示(MPP为最佳设计点)。计算这些点的概率密度函数值,并选取概率密度函数值最大的样本点,在其与坐标原点的连线得到一个以原点为起点的向量。在所得向量方向上采用线性搜索[18],由于是内插搜索,一般经过2~3次搜索便可确定该向量方向上与结构系统功能函数失效边界的近似交点,该交点到坐标原点的距离即为新的超球半径βi。
|
| 图 1 自适应策略获取最优化半径 Fig. 1 Adaptive strategy for obtaining optimal radius |
步骤5 筛选位于半径为βi-1的超球和半径为βi的超球之间的样本点,确定失效样本点。若样本点满足βi<‖uk‖≤βi-1,计算其对应的结构系统的极限状态函数值,并保留结果。对于满足条件g(uk)≤0的样本点,按照式(10)进行失效概率值的累加计算。
步骤6 重复步骤4和步骤5,直到收敛条件被满足[22],即可得到最优的超球半径βopt。
3.2 采用自适应超球重要抽样方法求解新指标为了准确地计算新指标δiP,从式(1)可以看出,关键问题在于计算结构系统的非条件失效概率Pf和条件失效概率Pf|Xi∈Ui(Q)。本节采用ARBIS方法来构建Pf和Pf|Xi∈Ui(Q)的求解算法。在构建的新算法中,含有截断输入变量Xi∈Ui(Q)的条件失效概率Pf|Xi∈Ui(Q)将被转化为不含截断输入变量的形式。经过这样的转化后,用于计算非条件失效概率Pf的ARBIS方法就能够很顺利地用来估计Pf|Xi∈Ui(Q),而不会增加额外的计算量。具体的转化过程如下所述。
当输入变量Xi缩减到区间Ui(Q)时,Xi就是一个截断变量,则所有输入变量的联合概率密度函数可表示为

|
(11) |
式中:K为截断系数,可表示为

|
(12) |
对于式(12)的估计,并不需要计算结构系统的功能函数值,其计算量可以忽略。因此,条件失效概率Pf|Xi∈Ui(Q)可重新表示为

|
(13) |
从式(13)中可以看出,条件失效概率Pf|Xi∈Ui(Q)的计算已转化为一个不含截断变量的多模态并联系统问题。经过这种转化,构建ARBIS方法计算新的矩独立重要性测度指标的算法如下:
步骤1 自适应搜索获取超球半径βopt,并计算无条件失效概率Pf;同时得到半径为βopt的超球外失效点组成的样本点矩阵B。
步骤2 当输入变量Xi缩减到区间Ui(Q)时,在样本点矩阵B中搜索输入变量Xi落在缩减区间Ui(Q)的样本点,记样本点个数为m。
步骤3 计算条件失效概率:
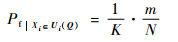
|
(14) |
式中:N为采用ARBIS方法的初始样本点个数。
步骤4 根据式(1)计算新的矩独立重要性测度指标δiP。
从上述步骤可以看出,ARBIS方法能够很容易地被用来计算新指标δiP,只需要一组输入变量的样本点就可以估计结构系统的非条件失效概率Pf和条件失效概率Pf|Xi∈Ui(Q),而不需要增加额外的计算量。因此,本节所提出的ARBIS方法相比DLRS MC方法计算效率得到很大提高。
4 算例分析 4.1 数值算例某一结构系统的功能函数可表示为
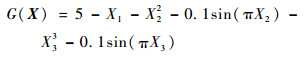
|
(15) |
式中:X1、X2和X3为相互独立的输入随机变量,均服从标准正态分布,即Xi~N(0, 1), i=1, 2, 3。
采用DLRS MC方法和ARBIS方法计算的新的矩独立重要性测度指标δiP值列于表 1中,每种方法的计算误差用标准差SD表示。
| 随机变量 | DLRS MC方法 | ARBIS方法 | |||
| δiP/10-2 | SD/10-2 | δiP/10-2 | SD/10-2 | ||
| X1 | 0.061 0 | 0.010 | 0.058 2 | 0.048 | |
| X2 | 0.226 4 | 0.007 | 0.216 7 | 0.013 | |
| X3 | 1.257 2 | 0.035 | 1.217 4 | 0.039 | |
| 计算量 | 446 000 | 2 619 |
|||
DLRS MC方法的计算结果可以看作参考精确解。从表 1可以看出,ARBIS方法计算得到的结果与DLRS MC方法计算结果基本相同。为了说明2种算法计算过程的收敛性,图 2给出了采用2种算法计算δiP值的标准差。可以看出,当2种算法计算结果均收敛时,ARBIS方法计算量远小于DLRS MC方法,计算效率提高很多。

|
| 图 2 DLRS MC方法和ARBIS方法计算的新的矩独立重要性测度指标的收敛曲线 Fig. 2 Convergence curves of new moment-independent importance measure indices of numerical example computed by DLRS MC and ARBIS methods |
从表 1可以看出,采用DLRS MC方法和AR-BIS方法计算的新的矩独立重要性测度指标δiP的重要性排序相同:X3>X2>X1。这表明当3个输入变量在各自的分布区域内缩减变化时,X3对于结构系统失效概率的影响程度最大。
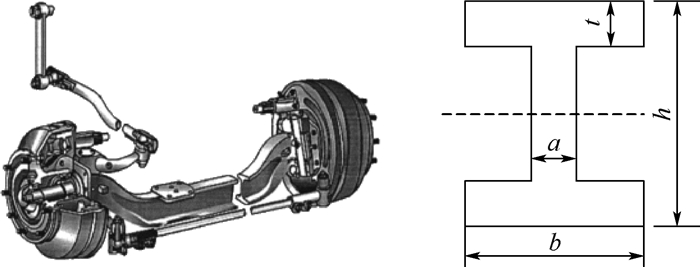
4.2 工程算例在汽车结构中,车桥承载着大部分汽车重量,其通过悬臂与车架相接,将来自车轮的牵引力和制动力,还有侧向力经过悬架传递给车架,起主要承载作用的就是汽车前轴[23]。由于工字型截断梁能够提高抗弯强度,因此前轴通常采用工字结构梁。
图 3为前轴的结构示意图。危险截面处的最大正应力为σ=M/Wx,最大切应力为τ=T/Wρ,M为弯矩,T为扭矩,Wx为截面系数,Wρ为极截面系数,且有
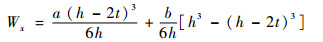
|
(16) |
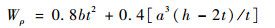
|
(17) |
|
| 图 3 汽车前轴结构示意图 Fig. 3 Schematic of automobile front axle structure |
考虑前轴结构静强度失效,有以下极限状态方程:
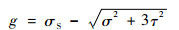
|
(18) |
式中:σS为静强度屈服极限,根据前轴材料特性有σS=460 MPa; g为裕度值。
前轴结构尺寸参数和承受外载看作独立正态随机变量,分布参数如表 2所示。
| 随机变量 | 均值 | 标准差 |
| a/mm | 12 | 0.60 |
| b/mm | 65 | 3.25 |
| t/mm | 14 | 0.70 |
| h/mm | 85 | 4.25 |
| M/(N·mm) | 3.5×106 | 7.5×105 |
| T/(N·mm) | 3.1×106 | 1.5×105 |
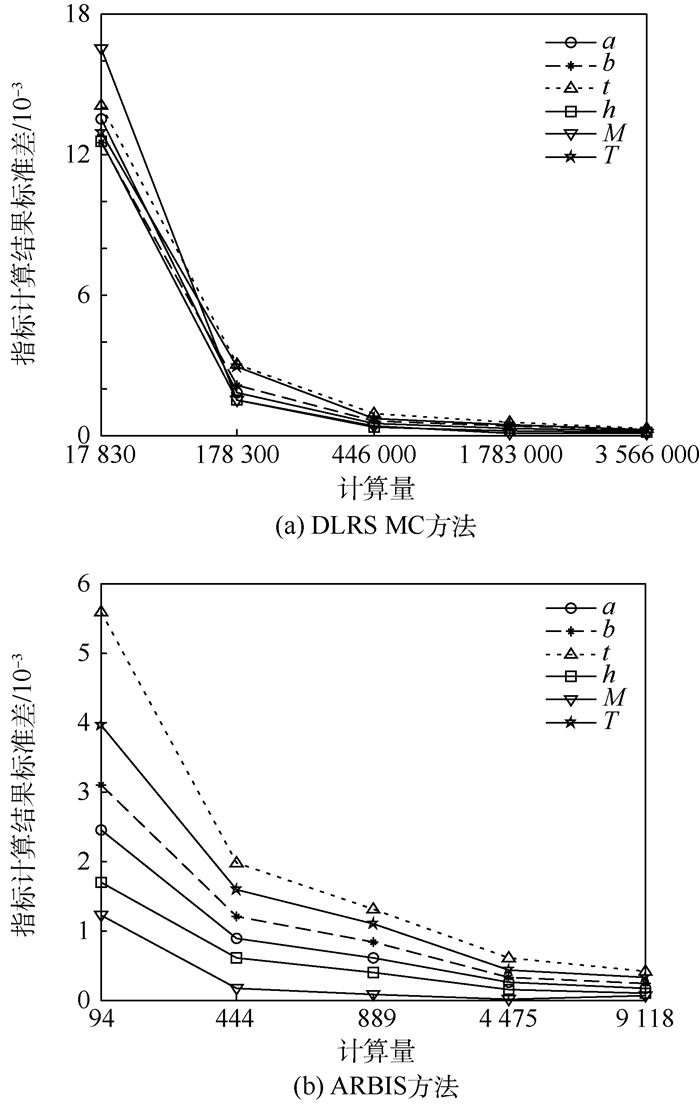
采用DLRS MC方法和ARBIS方法计算的新的矩独立重要性测度指标结果如表 3所示,同时也给出了计算功能函数的总次数。可以看出,2种算法计算结果相近。图 4给出了DLRS MC方法和ARBIS方法计算结果标准差的收敛曲线。可见,估计值的标准差都比较小,因此计算结果可靠稳健。DLRS MC方法的总次数为446 000,而ARBIS方法计算总次数仅为4 475,因此ARBIS方法的计算效率很高。
| 随机变量 | DLRS MC方法 | ARBIS方法 | |||
| δiP | SD/10-3 | δiP | SD/10-3 | ||
| a | 0.004 9 | 0.276 | 0.004 7 | 0.249 | |
| b | 0.006 4 | 0.394 | 0.006 2 | 0.333 | |
| t | 0.016 3 | 0.546 | 0.015 7 | 0.608 | |
| h | 0.001 4 | 0.173 | 0.001 3 | 0.149 | |
| M | 6.49×10-5 | 0.092 | 1.95×10-5 | 0.012 | |
| T | 0.009 5 | 0.426 | 0.009 2 | 0.321 | |
| 计算量 | 446 000 | 4 475 |
|||
|
| 图 4 DLRS MC方法和ARBIS方法计算汽车前轴的收敛曲线 Fig. 4 Convergence curves of automobile front axle computed by DLRS MC and ARBIS methods |
2种算法计算的新的矩独立重要性测度指标的排序均相同:t>T>b>a>h>M。这表明当分别固定6个输入随机变量在其各自的分布区域内缩减变化时,t对汽车前轴结构的失效概率影响程度最大,而M对其失效概率的影响几乎可以忽略不计。
5 结论本文提出了一种新的基于失效概率的矩独立重要性测度分析方法来计算输入随机变量对结构系统输出响应失效概率的平均影响程度。
1) 建立了一种新的区间划分技术来等可能地获得输入随机变量所有可能的缩减区间,并给出了相应证明。
2) 引入了自适应超球重要抽样方法来进行新指标的求解,提高了计算效率。
3) 给出了一个数值算例和一个工程算例,说明了本文所提新指标的意义,同时也验证了新算法的高效性。
附录A由于Q=[H1, H2, …, Hk, …, HN]T,同时P{Hk}=1/N成立,则有以下推导成立:
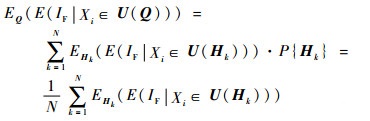
|
(A1) |
式中:
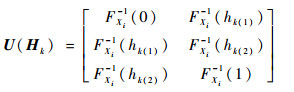
|
(A2) |
由指示函数期望E(IF)的定义,可以进行如下推导:
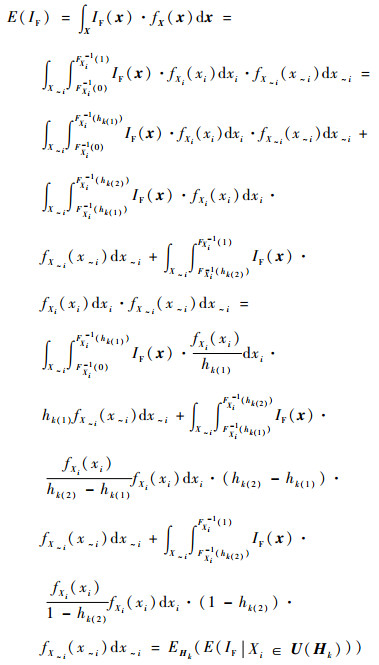
|
(A3) |
将式(A3)代入式(A1)中,就可以得到如式(A4)所示的区间上的全期望公式:

|
(A4) |
| [1] |
CASTILLO E, MINGUEZ R, CASTILLO C. Sensitivity analysis in optimization and reliability problems[J]. Reliability Engineering & System Safety, 2008, 93(12): 1788-1800. |
| [2] |
WEI P, LV Z, HAO W, et al. Efficient sampling methods for global reliability sensitivity analysis[J]. Computer Physics Communications, 2012, 183(8): 1728-1743. DOI:10.1016/j.cpc.2012.03.014 |
| [3] |
SALTELLI A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579-590. |
| [4] |
BJERAGER P, KRENK S. Parametric sensitivity in first order reliability theory[J]. Journal of Engineering Mechanics, 1989, 115(7): 1577-1582. DOI:10.1061/(ASCE)0733-9399(1989)115:7(1577) |
| [5] |
CAMPOLONGO F, SALTELLI A. Sensitivity analysis of an environmental model:An application of different analysis methods[J]. Reliability Engineering & System Safety, 1997, 57(1): 49-69. |
| [6] |
SALTELLI A, RATTO M, TARANTOLA S, et al. Sensitivity analysis for chemical models[J]. Chemical Reviews, 2005, 105(7): 2811-2828. DOI:10.1021/cr040659d |
| [7] |
BORGONOVO E, TARANTOLA S. Moment independent and variance-based sensitivity analysis with correlations:An application to the stability of a chemical reactor[J]. International Journal of Chemical Kinetics, 2008, 40(11): 687-698. DOI:10.1002/kin.v40:11 |
| [8] |
VAN GRIENSVEN A, MEIXNER T, GRUNWALD S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models[J]. Journal of Hydrology, 2006, 324(1): 10-23. |
| [9] |
SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28(2): 229-253. |
| [10] |
HELTON J C. Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal[J]. Reliability Engineering & System Safety, 1993, 42(2): 327-367. |
| [11] |
SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1): 271-280. |
| [12] |
IMAN R L, HORA S C. A robust measure of uncertainty importance for use in fault tree system analysis[J]. Risk Analysis, 1990, 10(3): 401-406. |
| [13] |
HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69. |
| [14] |
BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784. |
| [15] |
LIU H, CHEN W, SUDJIANTO A. Relative entropy based method for probabilistic sensitivity analysis in engineering design[J]. Journal of Mechanical Design, 2006, 128(2): 326-336. |
| [16] |
LI L Y, LU Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38: 40-47. DOI:10.1016/j.strusafe.2012.04.001 |
| [17] |
WEI P, LU Z, SONG J. A new variance-based global sensitivity analysis technique[J]. Computer Physics Communications, 2013, 184(11): 2540-2551. DOI:10.1016/j.cpc.2013.07.006 |
| [18] |
GROOTEMAN F. Adaptive radial-based importance sampling method for structural reliability[J]. Structural Safety, 2008, 30(6): 533-542. DOI:10.1016/j.strusafe.2007.10.002 |
| [19] |
AU S K, BECK J L. A new adaptive importance sampling scheme for reliability calculations[J]. Structural Safety, 1999, 21(2): 135-158. DOI:10.1016/S0167-4730(99)00014-4 |
| [20] |
ROSENBLATT M. Remarks on a multivariate transformation[J]. The Annals of Mathematical Statistics, 1952, 23(3): 470-472. |
| [21] |
DER KIUREGHIAN A, LIU P L. Structural reliability under incomplete probability information[J]. Journal of Engineering Mechanics, 1986, 112(1): 85-104. |
| [22] |
吕震宙. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009: 160-178. LV Z Z. Reliability and reliability sensitivity analysis of structural mechanism[M]. Beijing: Science Press, 2009: 160-178. (in Chinese) |
| [23] |
CAI Z Y. Precision design of roll-forging die and its application in the forming of automobile front axles[J]. Journal of Materials Processing Technology, 2005, 168(1): 95-101. |



