绳系卫星系统是由系绳连接绳端卫星构成的空间系统[1]。绳系卫星系统表现出了广阔的应用前景,如空间发电、构建空间结构和拖拽离轨等,是近年来航天研究热点之一[2]。空间绳系拖拽离轨是借助飞网等机构抓捕,并利用系绳连接主星和目标,由主星机动,实现目标拖拽转移的新概念在轨操作技术[3-5]。在空间碎片主动移除技术中,空间绳系拖拽离轨是一种较为高效和具有应用前景的技术。
在实际拖拽离轨任务中,系绳的摆动会引起主星的扰动,进而影响整个系统的稳定,因此如何抑制离轨过程中的系绳摆动是拖拽离轨任务的一个关键问题。目前已有一些相关的理论研究但还不广泛。文献[6]进行了圆轨道上绳系系统捕捉目标的动力学研究。文献[7]进一步进行了双绳系系统进行碎片主动移除的动力学研究。基于直接算法的最优控制理论被广泛应用于系绳回收控制领域,直接算法以其通用性能够很好地实现非线性动力学过程控制而避免对动力学本身的讨论。在这一领域,Williams[8]、Wen等[9]的研究具有代表性。文献[10]研究得到绳系系统星体姿态摆动将激发系统高阶摆动并影响绳系系统的稳定,文献[11]对此提出保持系数张力下抑制废星姿态摆动的控制方法并且文献[12]对此方法进行了进一步研究。
绳系系统的运动学具有强非线性,而且拖拽离轨过程中存在许多约束。故而需要在考虑这些约束因素下设计合适的控制律抑制拖拽离轨过程中系绳摆动。从20世纪70年代开始,针对具有复杂约束优化需求的控制问题,多年来大量工业实际中的成功应用表现出预测控制在解决这类问题的优势[13-15]。本文针对霍曼变轨推力段的绳系系统系绳摆振抑制问题,建立了轨道平面内绳系系统动力学模型;以最优化结果为参考轨迹、非线性模型预测控制方法为基础设计绳系系统拖拽离轨过程系绳平稳控制律,并通过仿真验证了控制方法的跟踪能力。
1 绳系系统动力学建模 1.1 建模假设和坐标系定义为突出关键问题,做如下假设,主要考虑系绳和主星的面内姿态运动,即假设主星的滚转角、偏航角,以及系绳的面外摆角为小角度,目标视为质点;不考虑系绳的弹性和质量;忽略除重力外的其余空间干扰力,主动力仅考虑推力,作用于主星质心;忽略除重力梯度力矩外干扰力矩,控制力矩作用于主星。
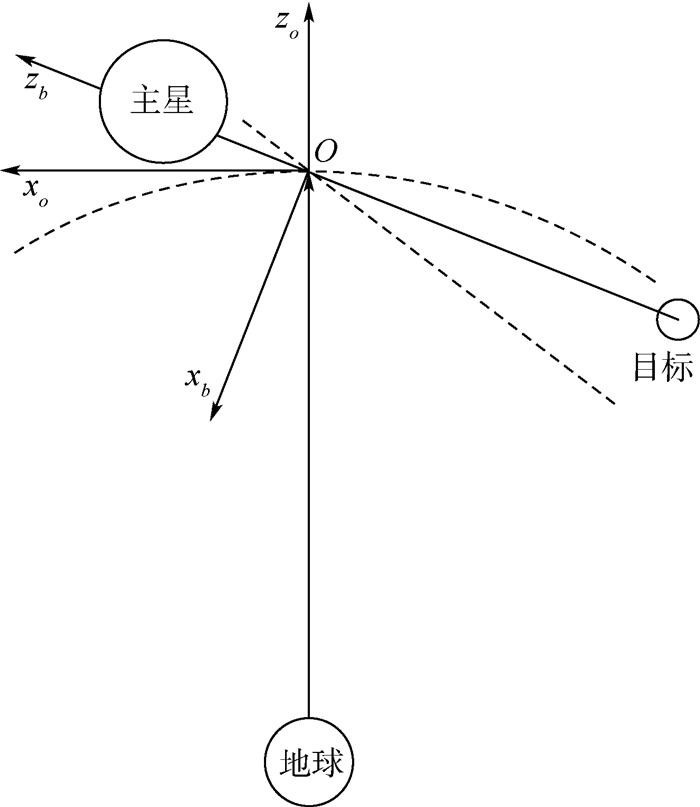
首先建立轨道坐标系So,zo轴沿地心连线方向由地球指向绳系卫星系统(TSS)质心,xo轴位于TSS质心轨道平面内与zo轴垂直并指向轨道运动方向,yo轴遵循右手准则,三轴单位矢量依次为eox、eoy和eoz。另外定义TSS本体坐标系Sb,zb轴沿着系绳指向主星,xb轴垂直系绳且在轨道平面内,三轴单位矢量依次为ebx、eby和ebz。为描述主星姿态运动,定义主星本体坐标系Sb1(三轴单位矢量依次为eb1x、eb1y和eb1z),记Sb1相对轨道坐标系So的滚动、俯仰和偏航角分别为φ1、θ1、ψ1(3—1—2旋转顺序)。绳系系统坐标系如图 1所示。
|
| 图 1 绳系系统坐标系示意图 Fig. 1 Schematic of coordinate system of tethered system |
利用上述假设,整个主星拖拽系统可以由包含系绳长度、系绳面内外摆角和主星姿态角,将动力学方程线性化,消去高阶项可以得到系统的动力学方程[16]。为简化研究,忽略系统面外运动,本文研究霍曼变轨的第一次推力过程,主星初始位于同步轨道,变轨目标为坟墓轨道,因此系统运行的椭圆轨道偏心率很小,可以认为是圆轨道。在偏置耦合力当中引入上述假设,并忽略包括二阶导数在内的高阶小量。
简化绳系系统的动力学方程式为[17]

|
(1) |
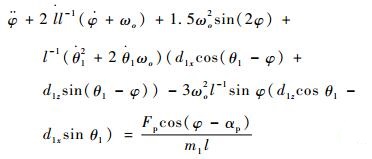
|
(2) |
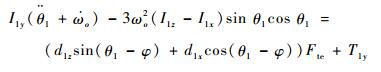
|
(3) |
式中:φ为系绳面内摆角(轨道坐标系So绕其y轴旋转φ得到TSS本体坐标系Sb);I1x、I1y和I1z为主星三轴惯量;T1y为主星y轴控制力矩大小;Fte为系绳张力;m1和m2分别为主星、子星的质量;m为系统总质量;l为系绳原长;ωo为轨道角速度;d1x、d1z分别为主星上x、z方向上的绳系点偏置大小;Fp为主星发动机推力大小;αp为主星发动机推力相对于轨道运动方向的夹角。动力学方程式(1)~式(3)形式较为简单,利用了小角度假设,因此仅供稳定控制器设计所用。
为处理方便,采用的无量纲时间和无量纲长度分别为

|
(4) |
式中:lt为单位绳长,可取为变轨前的TSS绳长。
做如下定义:
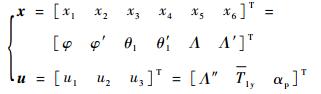
|
(5) |
式中:“′”代表对无量纲时间的导数;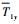
则可将式(5)转化为状态空间形式的系统动力学方程,x′=f(x, u)展开如下:

|
(6) |
式中: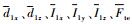
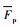
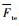
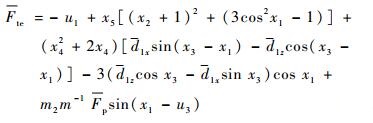
|
(7) |
参考轨迹采用最优化的方法求得。最优化方法一般描述为:寻找状态和控制,使得性能指标达到最小,同时满足包括系统状态方程,一系列始末约束和过程约束在内的所有约束条件。下面针对由主星俯仰运动和系绳面内摆振组成的主星系统面内运动,具体分析应采用的性能指标和应满足的约束条件,以建立最优问题。
2.1 性能函数选取希望在最短的时间内完成所需的脉冲,因此将问题视为时间最短的最优问题,其性能函数为
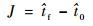
|
(8) |
式中: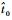
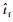
1) 始末约束
在开始变轨推力之前,绳系系统初值为
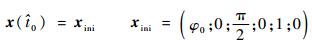
|
(9) |
式中:φ0为系绳面内摆角初值,π/2-φmax≤φ0≤π/2+φmax,φmax为系绳面内摆角所允许的最大幅值。
变轨推力结束之后,绳系系统回到水平状态,且绳长变化在可接受的范围内,终值状态如下:
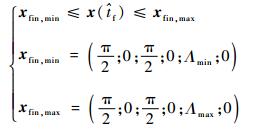
|
(10) |
式中:Λmin为出于防碰撞安全考虑所定义的最短无量纲绳长;Λmax为硬件所限最大的无量纲绳长。
2) 过程约束
系统的状态变量应满足系统动力学方程。对于控制量实际上也必然是有一个限度的。对控制量的约束这里主要考虑主星发动机推力方向φp的约束。
为了保证安全性,约束如下:
系绳面内摆角π/2-φmax≤φ≤π/2+φmax;主星俯仰角π/2-θ1max≤θ1≤π/2+θ1max;主星发动机推力方向αp, min≤αp≤αp, max;优化过程中对其他工程中重要性更低的量不做约束。其中φmax为系绳面内摆角所允许的最大幅值;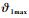
最后,整个推力段为避免系绳松弛,系绳的张力为非负。
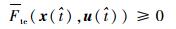
|
(11) |
3) 时间约束
显然推力时间不可能是不受限的,最短时间应为推力方向一直维持轨道速度方向时,达到所需速度增量的时间,其表达式为
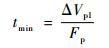
|
(12) |
式中:ΔVp1为主星霍曼变轨第一段所需速度增量,其表达式为
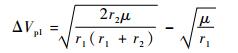
|
(13) |
其中:r1和r2分别为变轨前后的轨道半径。
最大时间可人为设定,无量纲化即有
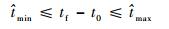
|
(14) |
4) 推力约束
假定推力时间相对轨道周期而言很小(这个假设在同步轨道是成立的),有限推力段在整个变轨过程中可以等效为脉冲推力,则推力提供的冲量在轨道方向应提供霍曼变轨所计算的速度增量,而在垂直轨道方向为0,即
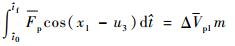
|
(15) |
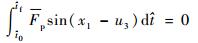
|
(16) |
至此,系统面内运动的最优控制问题已经建立:寻找满足控制约束的状态和控制集合,使得如式(8)所示的性能指标最小。
2.3 最优问题求解本研究采用Legendre-Gauss-Lobatto(LGL)伪谱法,直接LGL伪谱法是目前应用最广的伪谱方法之一[18],具有较高的收敛速度并且能方便地处理高阶导数,本文仅将此方法作为求解参考轨迹的方法,优化方法本身不是本文的重点。通过伪谱法将问题化为一个带约束的非线性规划问题,有成熟的寻优方法可以利用,本文采用MATLAB软件自嵌的函数fmincon进行求解。通过求解这个最优控制问题得到参考轨迹。
3 基于非线性模型预测控制律设计 3.1 模型离散化为了设计控制器,首先要将连续时间系统模型转化为离散时间系统。将第1节得到的非线性连续时间系统x′=f(x, u)在(x(t), u(t-1))处线性化得到如下线性时变系统[19]:
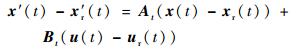
|
(17) |
式中:xr(t)为参考状态;ur(t)为参考控制量,由第1节给出; At和Bt的计算公式如下:
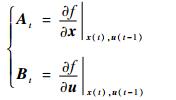
|
(18) |
设定系统的采样周期为T,得到离散化系统如下[20]:
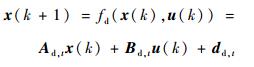
|
(19) |
式中:
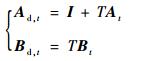
|
(20) |
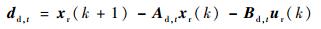
|
(21) |
其中:I为单位向量。
3.2 性能函数选取模型预测控制的目标就是跟踪期望的主星的三轴姿态和系绳摆角,即跟踪参考轨迹。在离轨拖拽过程中,对于给定的主星参考姿态及系绳参考摆角,使得在空间拖拽过程中,主星姿态和系绳摆角的模型预测控制下的轨迹与最优化得到的参考轨迹相同。因此以主星姿态和系绳摆角速度跟踪误差、控制力矩和终端误差作为优化目标,建立性能函数如下[15]:
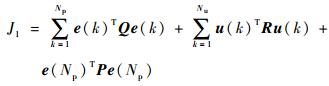
|
(22) |
式中:e(k)为跟踪误差;Q、R和P为相应的跟踪误差、控制量和终端加权矩阵;Np和Nu分别为预测和控制时域。
3.3 主星姿态和系绳摆角的预测利用绳系系统当前时刻k的信息x(k),包括主星姿态、系绳绳长和绳长变化,得到k时刻非线性离散状态空间模型如下[20]:
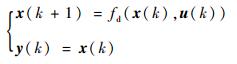
|
(23) |
式中:u(k)为k时刻控制量,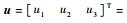
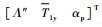
设定预测时域为Np,则可以根据绳系系统的当前状态信息,利用离散化的绳系系统动力学及运动学方程,经过迭代计算,得到预测时域Np内的绳系系统状态信息:
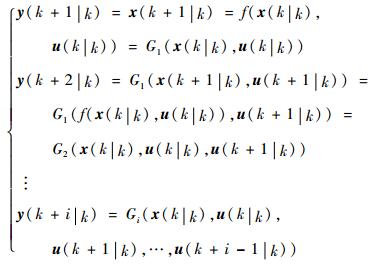
|
(24) |
式中:x(k|k)=x(k);y(k+i|k)为k时刻对未来k+i时刻系统输出y(k+i)的预测值;u(k+i|k)为k时刻计算k+i时刻作用于系统的控制量。
因此得到预测时域Np内的控制量{u(k), u(k+1), …, u(k+Np-1)}。同时假设在区间[Np,Nu]内控制量保持不变,则可以得到
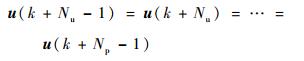
|
(25) |
因此利用绳系系统状态模型和系统过去的控制量或输出量,通过以上迭代计算出系统Np步预测输出为
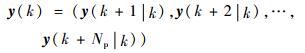
|
(26) |
1) 始末约束
在开始变轨推力之前,绳系系统处于水平状态,变轨推力结束之后,绳系系统回到水平状态,这里约束和求解最优问题中的相同。
2) 过程约束
系统的状态变量应满足系统动力学方程。
模型预测控制过程约束包含跟踪误差的约束,对于状态过程跟踪误差约束如下:
系绳面内摆角跟踪误差-Δφmax≤Δφ≤Δφmax;主星俯仰运动跟踪误差-Δθ1max≤Δθ1≤Δθ1max。
优化过程中对其他工程中重要性更低的量不做约束。其中Δφmax为系绳面内摆角跟踪误差所允许的最大幅值;Δθ1max为主星俯仰运动跟踪误差所允许的最大幅值。
系绳张力约束与最优问题中约束相同。
3) 推力约束
这里约束和求解最优问题中的相同。
3.5 非线性模型预测控制律实现为了方便运算,将跟踪误差加权矩阵、控制力矩加权矩阵和终端加权矩阵设计为单位矩阵。并由式(19)和以上步骤可以形成如下满足目标所要求的约束条件的绳系系绳摆振抑制控制的优化问题[15]。
寻找向量参数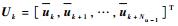
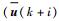
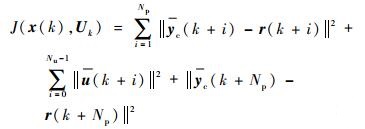
|
(27) |
式中: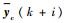
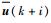
同样通过伪谱法将问题化为一个带约束的非线性规划问题,并采用MATLAB软件自嵌的函数fmincon进行求解。
根据模型预测控制原理,把求解所得的最优解的第1个元素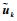
取仿真参数如下:主星初始俯仰角为90°(90°为水平),俯仰角速度为0;系绳初始摆角85°(90°为水平),初始摆角速度为0。且绳系系统参数如表 1所示。
| 参数 | 数值 |
| 主星发动机推力/N | 100 |
| 主星质量/kg | 100 |
| 主星惯量/(kg·m2) | 166.67 |
| 拖拽目标质量/kg | 8 |
| 系绳未拉伸长度/m | 200 |
设定拖拽约束要求如下:最短绳长10m,最大绳长1000m;主星的姿态角摆动幅度不大于2°,姿态角速度不大于0.2 (°)/s;系绳摆动幅度不大于5 (°)/s,摆动角速度不大于0.2 (°)/s。主星推力方向最小值-π/4,主星推力方向最大值π/4。
设定模型预测控制误差约束:系绳面内摆角跟踪误差所允许的最大幅值0.1°;主星俯仰运动跟踪误差所允许的最大幅值0.1°。
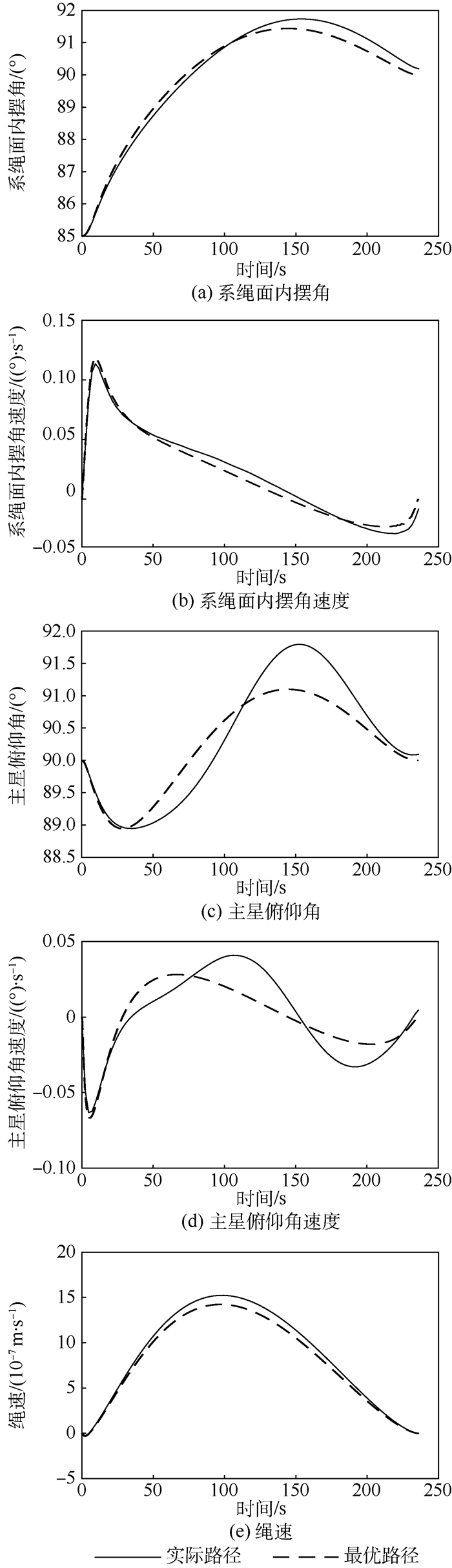
通过最优化方法求的最优轨迹即参考轨迹如图 2所示。使用模型预测控制得到的跟踪路径和最优化得到的参考轨迹的对比,如图 3所示。
|
| 图 2 系绳面内摆角、系绳面内摆角速度、主星俯仰角、主星俯仰角速度和绳速的实际路径和最优路径 Fig. 2 Actual path and optimal path of tether's in-plane swing angle, tether's in-plane swing angular velocity, main satellite pitching angle, main satellite pitching angular velocity and tether speed |
|
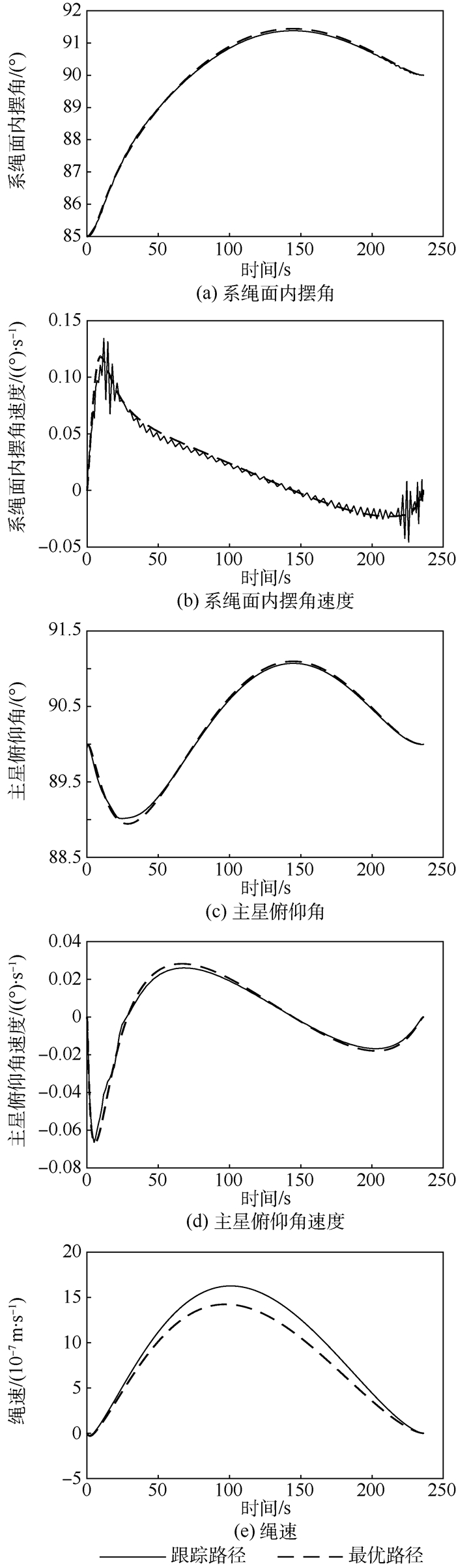
| 图 3 系绳面内摆角、系绳面内摆角速度、主星俯仰角、主星俯仰角速度和绳速的跟踪路径和最优路径 Fig. 3 Tracking path and optimal path of tether's in-plane swing angle, tether's in-plane swing angular velocity, main satellite pitching angle, main satellite pitching angular velocity and tether speed |
从图 2中不难发现:采用最优化方法得到的参考轨迹能使实际离轨拖拽绳系系统回到水平位置,并使系绳面内摆角和主星俯仰角满足约束要求,且系绳出于紧绷状态。而且过程比较平滑。说明最优化得到的参考轨迹是可用的。
从图 3中可以看到:模型预测控制下的跟踪路径的各状态很好地跟踪了最优路径即最优化得到的参考路径。并且绳系系统的状态控制在了约束范围内,即系绳面内摆角和主星俯仰角满足约束要求且系绳出于紧绷状态。而且明显可以通过缩小误差约束范围来提高跟踪效果,但这样又势必提高计算量。又能从图 3看到,模型预测控制下的除了系绳面内摆角速度外,其他跟踪路径比较平滑,但系绳面内摆角速度抖动比较厉害,不够平滑,如工程需要,须在跟踪控制中对摆角速度误差适当约束。模型预测算法具有在线优化的特点,鲁棒性较好,但是其计算量较大的问题需要在今后进一步研究。
5 结论1) 考虑主星姿态、系绳摆角稳定、系绳张力为正、系绳长度变化有限等约束,针对绳系系统拖拽离轨推力作用过程中系绳摆振的抑制问题,进行系统状态的最优轨迹求解,最优轨迹在满足变轨速度增量要求的同时实现了推力时间最短。
2) 仿真结果表明,所设计的非线性模型预测控制方法很好地跟踪了最优轨迹,并且满足控制约束条件;在变轨推力作用下主星姿态和系绳摆动稳定,且动态过程平滑。
| [1] |
朱仁璋, 雷达, 林华宝. 绳系卫星系统复杂模型研究[J]. 宇航学报, 1999, 20(3): 7-12. ZHU R Z, LEI D, LING H B. A sophisticated dynamical model of tethered satellite systems[J]. Journal of Astronautics, 1999, 20(3): 7-12. DOI:10.3321/j.issn:1000-1328.1999.03.002 (in Chinese) |
| [2] |
钟睿, 徐世杰. 基于直接配点法的绳系卫星系统变轨控制[J]. 航空学报, 2010, 31(3): 572-578. ZHONG R, XU S J. Orbit-transfer control for TSS using direct collocation method[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 572-578. (in Chinese) |
| [3] |
XU W, LIANG B, GAO D, et al.A space robotic system used for on-orbit servicing in the geostationary orbit[C]//Proceedings of 2010 International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2010: 4089-4094.
|
| [4] |
MANKALA K K, AGRAWAL S K. Dynamic modeling and simulation of impact in tether net/gripper systems[J]. Multibody System Dynamics, 2004, 11(3): 235-250. DOI:10.1023/B:MUBO.0000029393.25494.64 |
| [5] |
刘海涛, 杨乐平, 张青斌, 等. 地球静止轨道废弃卫星绳系拖曳离轨研究[J]. 中国科学:技术科学, 2012, 42(7): 780-787. LIU H T, YANG L P, ZHANG Q B, et al. An investigation on tether-tugging de-orbit of defunct geostationary satellites[J]. Scientia Sinica Technologica, 2012, 42(7): 780-787. (in Chinese) |
| [6] |
ZHAI G, ZHANG J, YAO Z. Circular orbit target capture using space tether-net system[J]. Mathematical Problems in Engineering, 2013, 2013(4): 87-118. |
| [7] |
QI R, MISRA A K, ZUO Z. Active debris removal using double-tethered space-tug system[J]. Journal of Guidance, Control, and Guidance, 2016, 40(3): 1-9. |
| [8] |
WILLIAMS P.Optimal control of a tethered payload capture maneuver[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston: AIAA, 2005: 1-23.
|
| [9] |
WEN H, JIN D P, HU H Y. Infinite-horizon control for retrieving a tethered subsatellite via an elastic tether[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4): 899-906. DOI:10.2514/1.33224 |
| [10] |
王晓宇, 金栋平. 计入姿态的绳系卫星概周期振动[J]. 振动工程学报, 2010, 23(4): 361-365. WANG X Y, JIN D P. Quasi-periodic oscil lation of a tethered subsatell ite with attitude[J]. Journal of Vibration Engineering, 2010, 23(4): 361-365. DOI:10.3969/j.issn.1004-4523.2010.04.001 (in Chinese) |
| [11] |
ZHAO G W, TANG B, SUN L, et al. Effect and control of pendular motion of abandoned satellite on tether drag system[J]. Applied Mechanics & Materials, 2014, 513-517: 3900-3906. |
| [12] |
赵国伟, 张兴民, 唐斌, 等. 空间绳系拖拽系统摆动特性与平稳控制[J]. 北京航空航天大学学报, 2016, 42(4): 694-702. ZHAO G W, ZHANG X M, TANG B, et al. Properties of pendulum motion of tether tugging system and its stable control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(4): 694-702. (in Chinese) |
| [13] |
QIN S J, BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 11(7): 733-764. DOI:10.1016/S0967-0661(02)00186-7 |
| [14] |
席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236. XI Y G, LI D W, LIN S. Model predictive control-Status and challenges[J]. Acta Automatica Sinica, 2013, 39(3): 222-236. (in Chinese) |
| [15] |
范国伟, 常琳, 戴路, 等. 敏捷卫星姿态机动的非线性模型预测控制[J]. 光学精密工程, 2015, 23(8): 2318-2327. FAN G W, CHANG L, DAI L, et al. Nonlinear model predictive control of agile satellite attitude maneuver[J]. Optics and Precision Engineering, 2015, 23(8): 2318-2327. (in Chinese) |
| [16] |
LAKSHMANAN P K, MODI V J, MISRA A K. Dynamics and control of the tethered satellite system in the presence of offsets[J]. Acta Astronautica, 1987, 15(12): 1053-1057. DOI:10.1016/0094-5765(87)90031-2 |
| [17] |
ZHONG R, ZHU Z H. Timescale separate optimal control of tethered space-tug systems for space-debris removal[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(11): 2540-2545. DOI:10.2514/1.G001867 |
| [18] |
徐少兵, 李升波, 成波. 最优控制问题的Legendre伪谱法求解及其应用[J]. 控制与决策, 2014, 29(12): 2113-2120. XU S B, LI S B, CHENG B. Theory and application of Legendre pseudo-spectral method for solving optimal control problem[J]. Control and Decision, 2014, 29(12): 2113-2120. (in Chinese) |
| [19] |
孙银健.基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究[D].北京: 北京理工大学, 2015. SUN Y J.Research on model predictive control-based trajectory tracking algorithm for unmanned vehicles[D]. Beijing: Beijing Institute of Technology, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10007-1015030238.htm |
| [20] |
陈薇.非线性预测控制快速算法的研究与应用[D].合肥: 中国科学技术大学, 2007. CHEN W.Study and application of nonlinear model predictive control fast algorithm[D]. Hefei: University of Science and Technology of China, 2007(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10358-2007097280.htm |



