飞机上的连接结构大多数为多钉连接件,铆接又是飞机结构中经常使用的连接方式,飞机的一个连接结构上就可能有上百个铆钉,所以很难建立庞大的实体模型区进行细节应力分析。而且铆接过程是一个很复杂的过程,铆接完的部分材料已经进入塑性,并且铆钉和孔的部分区域存在干涉作用。所以,直接建立静力三维实体模型进行细节应力分析是不合理的。试验表明,对于连接件,在其他参数相同的情况下,铆接的紧固件比普通螺接的紧固件的刚度大得多[1]。铆接时孔壁强化是靠板材和钉杆的变形,即钉杆变形使孔径胀大[2]。铆接过程使得结构在整个使用期间铆钉和孔都会有效干涉。因此,需要先对铆接过程进行显示动力学分析,通过分析获得铆接后钉、孔的变形形式和干涉量。对多钉结构的细节应力分析,需要用到铆钉的载荷-位移(P-δ)曲线。
Ronsenfeld和Jarfall只是将P-δ曲线看做一条直线[3-4],用柔度系数来表征紧固件的变形和孔的局部变形。国外多名学者通过大量试验提出紧固件柔度的半经验公式[5-8]。试验表明,紧固件的P-δ曲线并不是一条直线,而是一条曲线。
可将P-δ曲线看成由线性段和非线性段2部分组成,而文献[5-8]只考虑了P-δ曲线直线段的刚度值。对于多钉连接件结构,如果一部分紧固件的钉载值处于P-δ曲线非线性段,而其余的钉载值处于线性段,只考虑线性段的影响无法满足需求。梁沛权[9]采用三维弹塑性有限元法分析计算全段P-δ曲线。陈涛等在此基础上运用通用有限元分析程序ANSYS计算得到了螺接连接件的紧固件全段P-δ曲线并且编制了APDL子程序[10],但这种程序只针对螺接连接件的形式,无法应用于飞机上大规模使用的铆接连接结构。
因为铆接的形式、材料种类和结构尺寸是多种多样的,所以目前利用试验获取的P-δ曲线虽然可信度高,但是成本却很高。此外,P-δ曲线对干涉量是比较敏感的,要想利用试验研究紧固件P-δ曲线,制造的试验件需要达到微米级的精度[10]。因此在文献[10]的基础上,本文首先对铆接过程进行显示动力学分析,其次建立三维实体模型计算P-δ曲线并且编制了APDL子程序,可快速计算各种形式的铆接连接件的紧固件P-δ曲线。在ANSYS中建立了钉单元,基于增量法,利用全段P-δ曲线,计算该连接件钉载并设计开发了多钉连接件细节应力分析系统,便于工程应用。最后用应力严重系数法估算连接件的疲劳寿命。开展典型航空铆接连接件疲劳试验,将试验结果与用本文方法估算所得寿命对比,结果显示计算结果与试验结果一致性良好,说明本文方法具有可靠性,可以在工程中推广。
1 紧固件P-δ曲线获取方法 1.1 铆接过程有限元分析获取准确的铆钉P-δ曲线要先建立模型分析铆接过程,得到铆钉和钉孔的配合形式和干涉量,图 1为铆钉几何模型。

|
| 图 1 铆钉几何模型 Fig. 1 Geometric model of rivets |
因为航空连接件的铆钉主要受到横向剪切作用,所以镦头部分的受力很小。同时,镦头部位的材料在压铆过程中被硬化,其弹性模量可以认为是不变的。铆接过程是一个动态过程,解析法难以得到精确结果,用LS-DYNA进行显式动力学分析[11-12]。对3种典型铆钉的铆接过程进行研究。
用4节点四边形平面单元PLANE162单元划分网格也可以退化为三角形平面单元。每个节点有6个自由度:沿x和y方向的位移、速度和加速度。划分网格时,网格的拓扑形状要与传力路线一致。同时,考虑到计算精度和计算规模的控制,将铆钉、孔壁附近区域和铆接件其他区域网格细化。
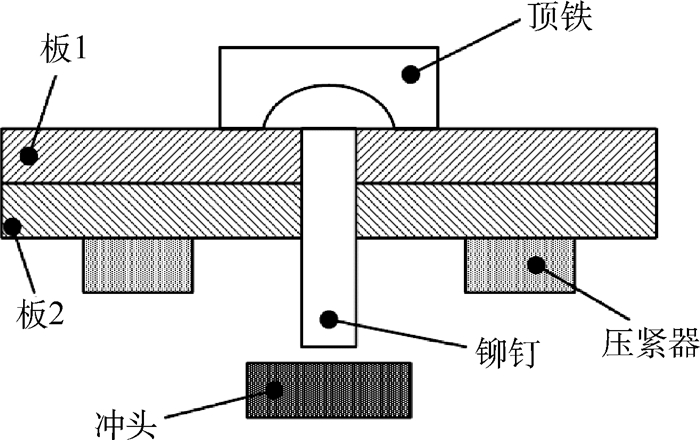
与隐式静力学分析不同,显式动力学分析的接触是变化的、复杂的。以铆接过程为例,初始阶段有冲头与铆钉端面的接触、顶铁与铆接件的接触、顶铁与铆钉头的接触以及铆钉头与铆接件的接触;之后又多了钉杆与孔壁的接触、镦头与铆接件的接触,并且接触的面积逐渐增大。铆接简化模型如图 2所示。
|
| 图 2 铆接简化模型 Fig. 2 Simplified model of riveting |
接触算法选用能自动搜索模型表面是否发生穿透的单面接触。此外,单面接触允许模型所有外表面接触,不需要定义接触面和目标面,能有效地处理压铆这种接触区域无法预测的大变形问题。接触类型选用二维自动接触(ASS2D),在计算时,既考虑到了壳单元两侧的接触,并且能自动确定接触表面的方向。随着接触点穿透目标面的深度增加,抵抗节点穿透的惩罚力将增大,并且只会增加到一个最大值。
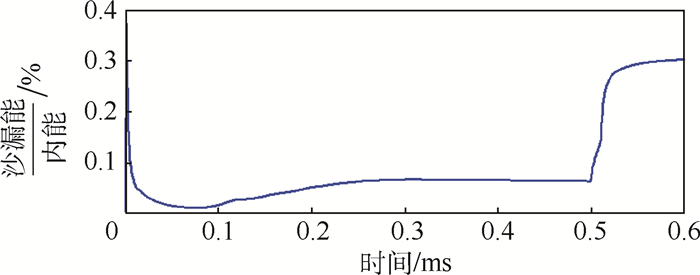
在进行显式动力学分析时,使用的PLANE162单元属于减缩积分单元,会产生沙漏模式,因此需要评估沙漏变形的影响。如图 3所示,铆接开始后,沙漏能与内能的比值不大于0.4%(≪10%),说明沙漏变形对计算结果的影响非常小,显式动力学分析的结果是合理的。
|
| 图 3 沙漏能与内能的比值 Fig. 3 Ratio of hourglass energy to internal energys |
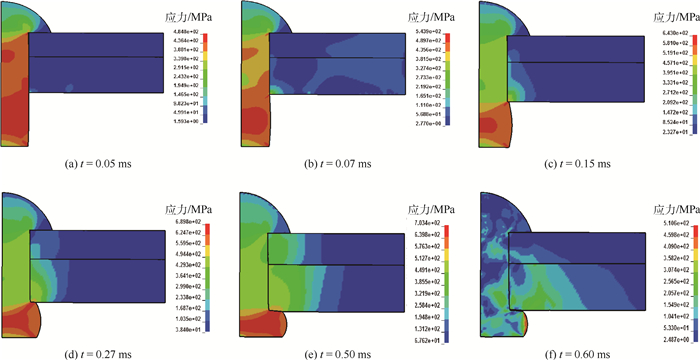
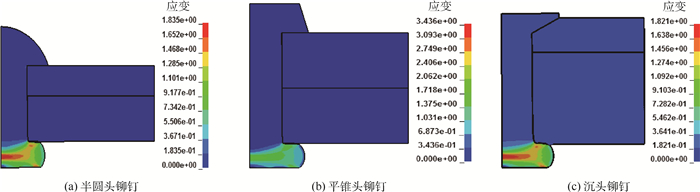
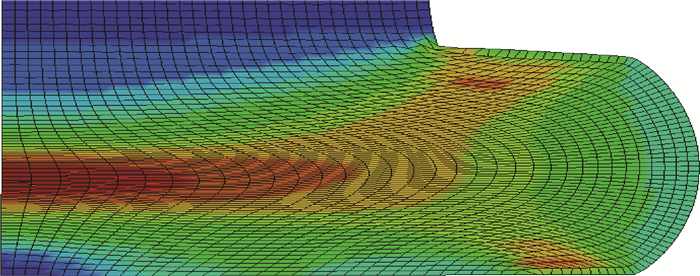
以半圆头铆钉为例,铆接过程中的应力分布如图 4所示。从图中可以看出:压紧器压紧后,铆钉杆刚好与孔壁接触时铆钉杆受力最严重,铆钉杆受到冲头的压力,铆接件右端受到压紧力(图 4(a));在镦头成型过程中,镦头受力变形最严重,同时孔壁受到了钉杆胀大的挤压力(图 4(b)~(e));冲头卸载后,铆钉和铆接件发生弹性回复,这个阶段镦头的材料进入塑性,钉杆和孔壁由于干涉作用相互挤压,孔壁两侧区域产生较大的应力(图 4(f))。铆接结束后塑性应变分布情况见图 5。从图中可知,模型只有镦头部分进入塑性。图 6为镦头部分网格变形与塑性应变分布,可见,网格的变形程度与塑性变形的程度是一致的,并且网格没有发生畸变。铆接后钉、孔的干涉量为由于铆钉杆镦粗而使孔胀大的量[13-15]。
|
| 图 4 半圆头铆钉铆接过程应力分布 Fig. 4 Stress distribution in riveting process of semicircular head rivet |
|
| 图 5 铆接后塑性应变分布 Fig. 5 Plastic strain distribution after riveting |
|
| 图 6 镦头部位网格变形 Fig. 6 Grid deformation of heading positon |
在有限元分析的基础上编制了APDL子程序,使用该子程序只需输入结构尺寸、材料等参数即可建立有限元模型,再输入载荷和位移条件即可进行有限元分析,铆接过程有限元分析参数化如图 7所示。
|
| 图 7 铆接过程有限元分析参数化 Fig. 7 Parametric finite element analysis of riveting process |
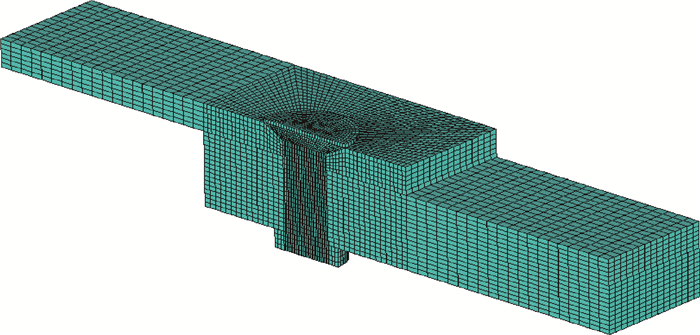
在铆接过程分析的基础上,建立了典型铆接连接件的几何模型,如图 8所示,并将尺寸参数化,网格划分选用SOLID186,以便用于不同尺寸连接件的有限元分析。
|
| 图 8 铆钉连接件几何模型 Fig. 8 Rivet connection geometric model |
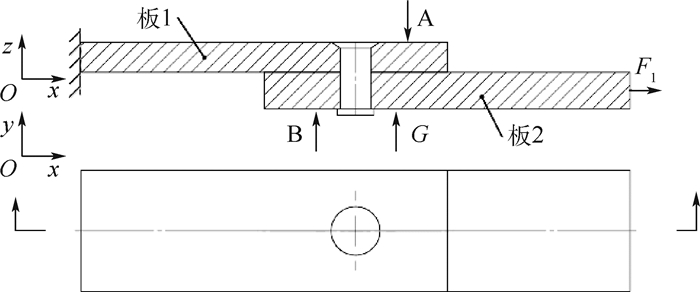
在接触方式选择方面,连接件实体模型的接触都是面-面接触,并且都是柔体-柔体接触。可以预见发生接触的部位包括铆钉帽与上下板之间、铆钉杆与孔壁之间以及上下板之间共5对接触。铆接件均为干涉配合,并且同一个铆钉与钉孔的干涉量存在2个:一个是上板钉孔与铆钉杆的干涉量,另一个是下板钉孔与铆钉杆的干涉量。为与试验结果进行对比,边界条件需要按照试件试验时的变形情况来设置。如图 9所示,F1为施加的外力,G为对截面的零位移约束, 板1和板2下端面受到z向正向的支持作用,并且在板1的A端和板2的B端施加夹紧力防止试件弯曲,所以在板1的下端面和板2下端面未与板1重叠的部分施加z向零位移约束。同时,在板1的左端面施加全位移约束,在板2的右端面施加拉力。由于试件关于xz平面对称,所以对这个平面的节点施加y方向的零位移约束。
|
| 图 9 边界条件 Fig. 9 Boundary conditions |
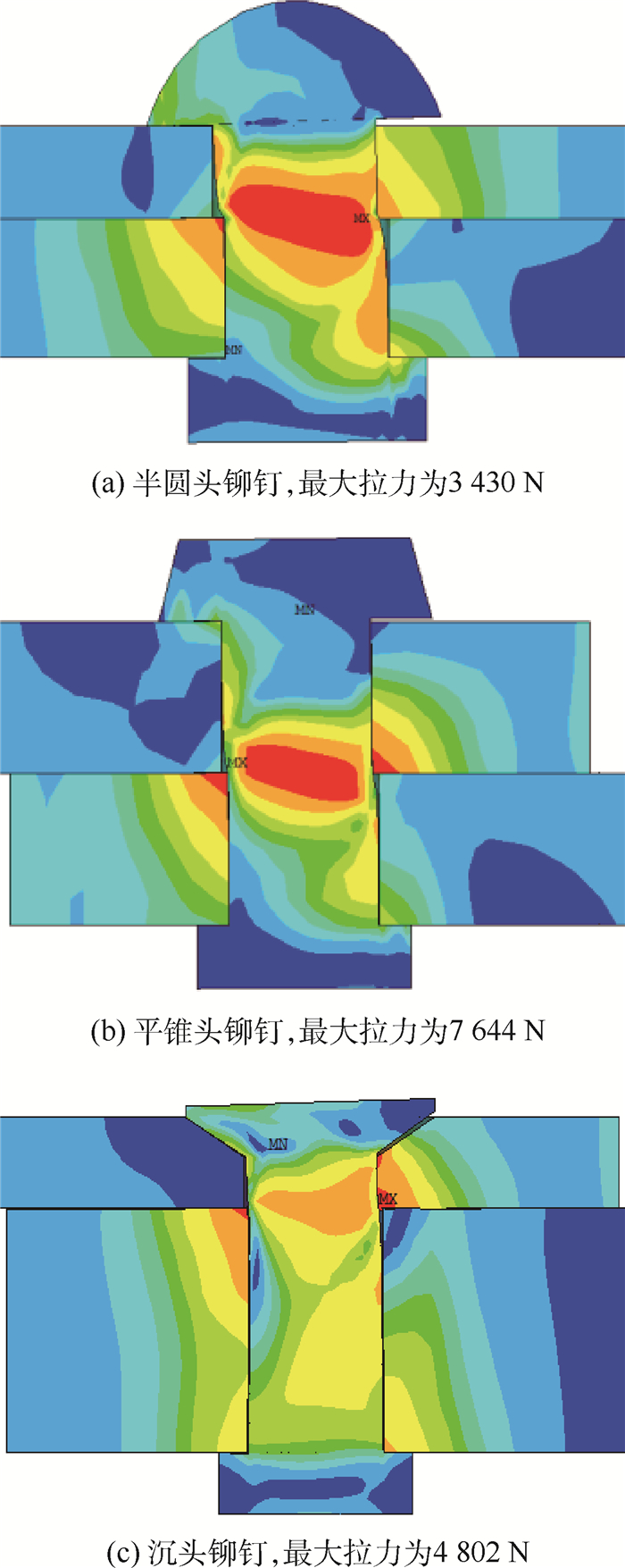
如图 10为3种形式铆钉在承受最大拉力时的局部应力和变形情况。可以看出,铆钉及附近区域的应力梯度最大,应力变化最复杂;铆钉主要承受剪力,所以受力最严重的部位均在两板交界处。且铆钉的预紧力可以忽略[10], 所以铆接件在受到最大载荷时,铆钉头右侧的部分区域已经与铆接件分离。
|
| 图 10 模型局部应力和变形 Fig. 10 Stress and deformation of part of model |
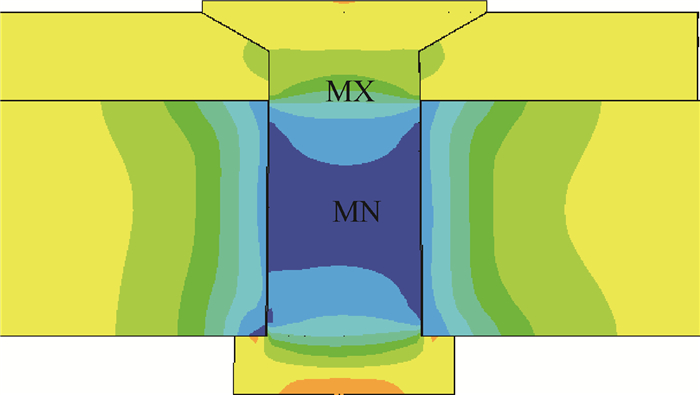
如图 11为不受力时的x方向应力分布,从图中可以看出,由于铆钉与钉孔的干涉作用,孔壁区域的材料受到较大的压力。同时,由于下板钉孔与铆钉的干涉量比上板的大,所以下板与铆钉接触的区域受到的压力明显大于上板[10]。
|
| 图 11 P=0 N时x方向应力分布 Fig. 11 Stress distribution along x direction when P=0 N |
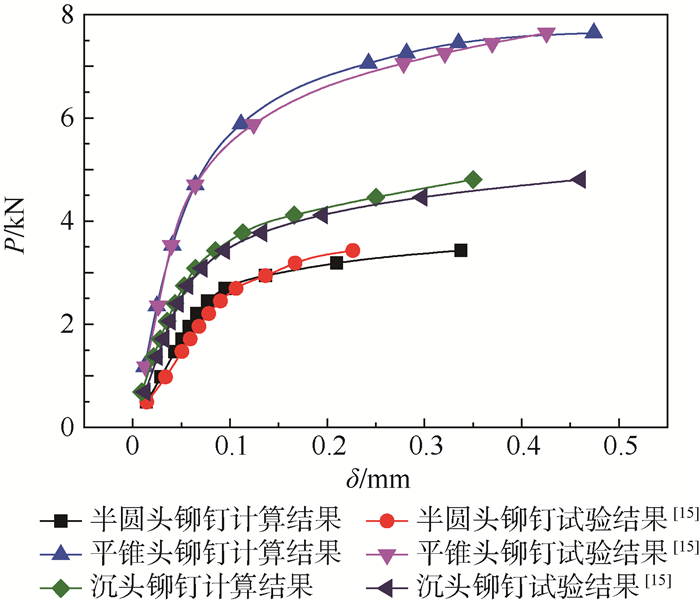
在计算铆接连接件的P-δ曲线时,由于干涉作用,使得连接件存在初始位移δ0。因此每个力对应的测量位移δi也需要减去干涉引起的初始位移δ0。计算得到的P-δ曲线和对应的试验曲线见图 12。试验曲线取自文献[15]。计算的结果与试验拟合得到的结果是比较接近的。说明本文计算铆钉的P-δ曲线方法是合理的,可以满足工程需求。
|
| 图 12 P-δ曲线计算结果与试验结果对比 Fig. 12 Comparison of P-δ curves between calculated and experimental results |
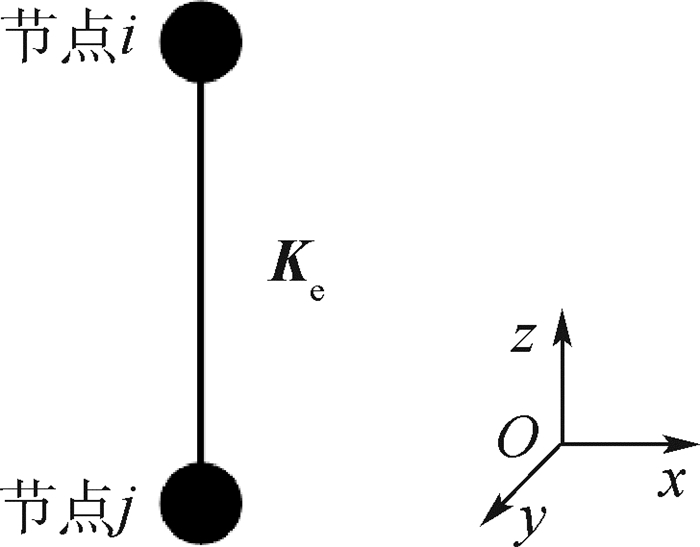
参考国内外学者针对多钉连接件细节应力分析方法开展的大量研究[16-18],在ANSYS中建立了钉单元简化模型,以提高计算效率, 如图 13所示, Ke为单元刚度矩阵。钉单元是指连接结构件的铆钉和螺栓,主要承受剪切载荷,可以将钉单元复杂的受力形式简化为只受x和y方向的载荷, 如图 14所示。
|
| 图 13 钉单元示意图 Fig. 13 Schematic diagram of rivet unit |

|
| 图 14 钉单元受力情况 Fig. 14 Loading situation of rivet unit |
在文献[1, 19]的基础上,将单元的自由度拓展为10个,2个节点各5个,分别为:沿x、y、z方向的位移,绕x轴和y轴的转动。将单元刚度方程表示为
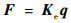
|
(1) |
式中:F为钉单元两端节点力矢量;q为钉单元节点的位移矢量。
对应到两节点,可展开为

|
(2) |
P-δ曲线是一条非线性变化的曲线,随着钉载的增大,钉元将进入非线性区,其刚度是一个不断变化的量,钉元刚度的改变将影响整个刚度矩阵,导致力的重新分配。采用增量法计算钉载的基本原理为[19-21]:将总外载Pa分为线性部分Pe和非线性部位Pp,即Pa=Pe+Pp,Pe是某一个钉元(或某些钉元)达到Pg(P-δ曲线线性段和非线性段临界点)时所对应的外载;Pe确定之后,根据精度要求将Pp分为相等的m段,每段外载为Pm,每次以Pm作为外载计算出所有钉元的内力,并检查是否进入P-δ曲线的非线性段,如果进入就修改该钉元的刚度系数。作m次计算,得到m段内力,一个钉的钉载就是各段计算结果的累加。
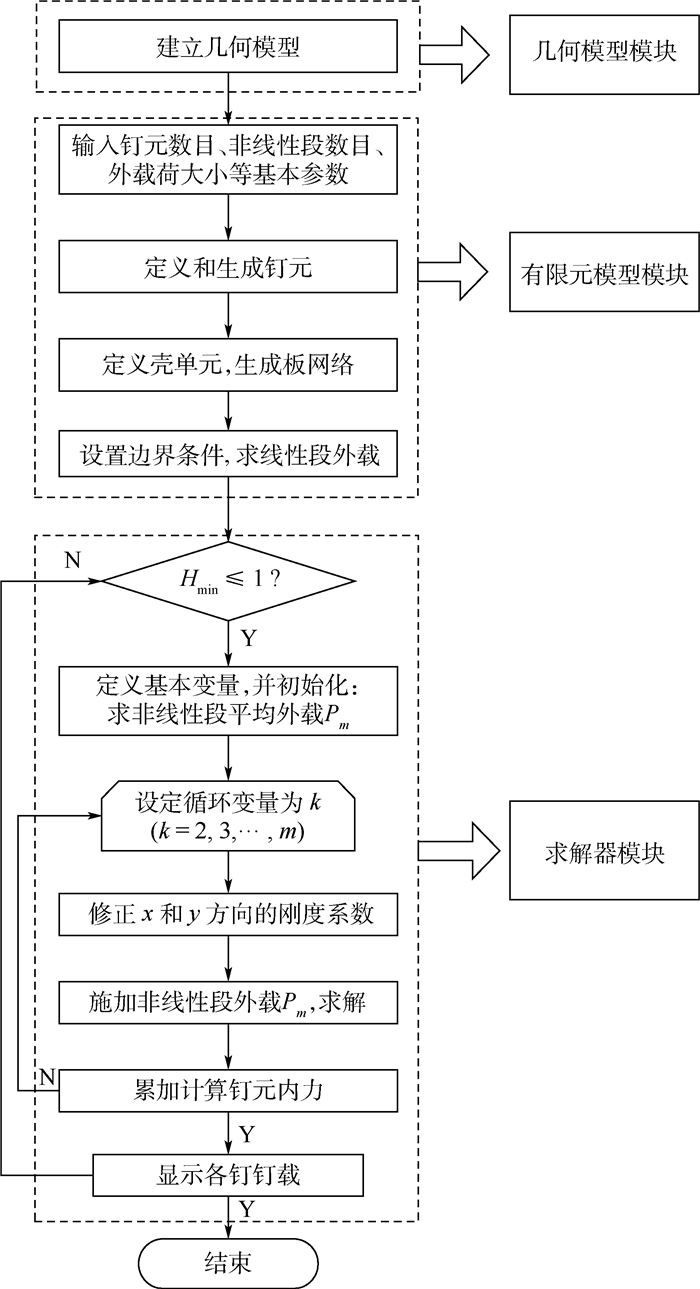
为高效分析,用APDL语言设计开发了多钉连接件细节应力分析系统,计算结果与解析结果相比误差小于13%。图 15为该系统的流程图, Hmin为外载和钉元内力的比值的最小值。
|
| 图 15 细节应力分析系统流程图 Fig. 15 Detailed stress analysis system flowchart |
试验对象为2A12-T4铝合金铆接搭接试件,铆钉为TB2-1钛合金100°小沉头铆钉,如图 16所示。钛合金材料TB2-1的基本性能参数见表 1。试件合计24件,分为6组,每组4件。每组试件均受等幅疲劳载荷作用,最大载荷24 kN,应力比为0,频率15 Hz。

|
| 图 16 试件结构形式与尺寸 Fig. 16 Structure form and dimension of specimen |
| 力学性能参数 | 数值 |
| 弹性模量/MPa | 85 000 |
| 泊松比 | 0.33 |
| 密度/(kg·m-3) | 4.83 |
| 屈服强度/MPa | 880 |
为与试验结果对比,试验前先用编制好的参数化模型计算P-δ曲线,再用多钉连接件细节应力分析系统计算钉载。有限元模型及各钉位置如图 17所示,分别计算6种加载情况下,受到最大和最小外载荷时的钉载。加载情况与疲劳试验加载情况对应一致。用应力严重系数法估算各钉疲劳寿命[22], 计算得3号钉孔为最危险部位。

|
| 图 17 有限元模型及各钉位置 Fig. 17 Finite element model and position of rivets |
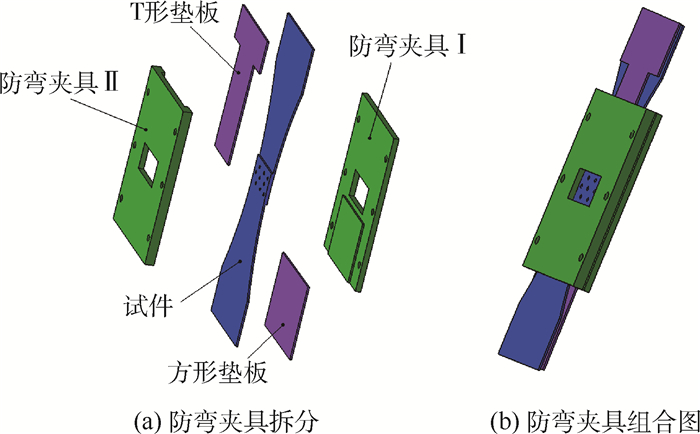
试件在受到拉伸载荷时,由于偏心力矩的作用会产生较大弯矩,为防止对铆钉产生影响,防止弯曲变形,使用防弯夹具如图 18所示。
|
| 图 18 防弯夹具 Fig. 18 Anti-bending fixture |
试验表明,初始裂纹萌生位置均在3号铆钉孔或1号铆钉孔处,这与计算预测的初始裂纹萌生位置非常吻合。断裂部位如图 19所示。疲劳试验结果与计算结果如表 2所示,误差在16%以内。

|
| 图 19 试件断裂部位 Fig. 19 Fracture parts of specimen |
| 组别 | 中值疲劳寿命/cycles | 计算与试验结果相对误差/% | |
| 试验结果 | 计算结果 | ||
| 1 | 192 909 | 169 489 | 12.14 |
| 2 | 72 598 | 64 937 | 10.55 |
| 3 | 41 271 | 35 886 | 13.05 |
| 4 | 277 469 | 312 001 | 12.45 |
| 5 | 121 505 | 140 670 | 15.77 |
| 6 | 52 113 | 59 389 | 13.96 |
4 结论
1) 应用显式动力学分析铆接过程是符合实际情况的。
2) 编制APDL子程序计算P-δ曲线的方法与试验相比,误差在合理的范围之内,从而改变了铆钉P-δ曲线的获取必须依赖试验的现状。
3) 建立钉元模型来估算多钉连接结构疲劳寿命的方法与试验结果比较吻合,能较准确地预测疲劳裂纹的初始位置,误差在工程应用允许的范围之内,可以在工程上推广。
| [1] |
飞机结构强度研究所.
航空结构连接件疲劳分析手册[M]. 西安: 飞机结构强度研究所, 1985: 21-23.
Aircraft Structure Strength Research Institute. Fatigue analysis manual of aircraftjoints[M]. Xi'an: Aircraft Structure Strength Research Institute, 1985: 21-23. (in Chinese) |
| [2] |
BOFF A.飞机制造工艺学[M].佘公藩, 张钧, 等译.西安: 西北工业大学出版社, 1989: 205-221.
BOFF A. Aircraft manufacturing technology[M].SHE G F, ZHANG J, et al., translated. Xi'an: Northwest Industrial University Press, 1989: 205-221(in Chinese). |
| [3] | ROSENFELDS J.Analytical and experimental investigation of bolted joints: NACA TN-1458[R].Washington, D.C.: NACA, 1458. |
| [4] | JARFALL L E. Optimun design of joints:The stress severity factor concept[J]. Aircraft Fatigue, 1967, 56 (2): 49–63. |
| [5] | TATE M B, ROSENFELD S J. Preliminary investigation of theloads carried by individual bolts in bolted joints: NACA TN-10511[R].Washington, D.C.: NACA, 1946. |
| [6] | NELSON W D, BUNIN B L, HART-SMITHL J. Critical joints in large composite aircraft structure: NASA CR-3710[R].Washington, D.C.: NASA, 1983. |
| [7] | SWIFT T.Fracture analysis of stiffened structure: ASTM STP842[R].New York: ASTM, 1984. |
| [8] | HUTH H.Influence of the fastener flexibility on the prediction of load transfer and fatigue life for multi-row joints: ASTM STP927[R].New York: ASTM, 1986. |
| [9] |
梁沛权.紧固件载荷-变形曲线的计算方法研究[D].西安: 西北工业大学, 1987.
LIANG P Q.Study on the numerical calculations of P-δ curves of fasteners[D]. Xi'an: Northwestern Polytechnical University, 1987(in Chinese). |
| [10] |
陈涛, 何宇廷, 韩宏文, 等. 螺栓连接件的紧固件P-δ曲线计算方法研究[J].
科学技术与工程, 2014, 14 (28): 140–147.
CHEN T, HE Y T, HAN H W, et al. Study on the numerical calculations of P-δ curves of fasteners for bolted joints[J]. Science Technology and Engineering, 2014, 14 (28): 140–147. DOI:10.3969/j.issn.1671-1815.2014.28.027 (in Chinese) |
| [11] |
师访.
ANSYS二次开发及应用实例详解[M]. 北京: 中国水利水电出版社, 2012: 121-126.
SHI F. Secondary development of ANSYS and detailed application example[M]. Beijing: China Water Power Press, 2012: 121-126. (in Chinese) |
| [12] |
王勖成.
有限单元法[M]. 北京: 清华大学出版社, 2009: 576-579.
WANG X C. Finite element method[M]. Beijing: Tsinghua University Press, 2009: 576-579. (in Chinese) |
| [13] |
袁立.
航空制造工程手册:飞机装配[M]. 北京: 航空工业出版社, 2010: 390-401.
YUAN L. Handbook of aeronautical manufacturing engineering:Aircraft assembly[M]. Beijing: Aviation Industry Press, 2010: 390-401. (in Chinese) |
| [14] |
熊竣江.
飞行器结构疲劳与寿命设计[M]. 北京: 北京航空航天大学出版社, 2004: 85-111.
XIONG J J. Structure fatigue and life design of aircraft[M]. Beijing: Beihang University Press, 2004: 85-111. (in Chinese) |
| [15] |
李艳, 于克杰, 李小雷. 铆钉材料对铆接变形影响的有限元分析[J].
机床与液压, 2013, 41 (4): 50–52.
LI Y, YU K J, LI X L. Finite element analysis for the influence of rivet materials on rivet deformation[J]. Machine Tool and Hydraulics, 2013, 41 (4): 50–52. DOI:10.3969/j.issn.1001-3881.2013.04.015 (in Chinese) |
| [16] | BARROIS W. Stresses and displacements due to load-transfer by fasteners instructural assemblies[J]. Engineering Fracture Mechanics, 1978, 10 (1): 115–176. DOI:10.1016/0013-7944(78)90055-3 |
| [17] | MCCARTHY M A, MCCARTHY C T, PADHI G S. A simple method for determining theeffects of bolt-hole clearance on load distribution in single-column, multi-bolt composite joints[J]. Composite Structures, 2006, 73 (1): 78–87. DOI:10.1016/j.compstruct.2005.01.028 |
| [18] | MCCARTHY C T, GRAY P J. An analytical model for the prediction of loaddistribution in highly torqued multi-bolt composite joints[J]. Composite Structures, 2011, 92 (2): 287–298. |
| [19] |
郑晓玲.
民机结构耐久性与损伤容限设计手册[M]. 北京: 航空工业出版社, 2003: 38-44.
ZHENG X L. Handbook of civil aircraft structures durability and damage tolerance design[M]. Beijing: Aviation Industry Press, 2003: 38-44. (in Chinese) |
| [20] |
薛景川, 杨玉功.
紧固件载荷变形曲线的试验方法[M]. 西安: 飞机结构强度研究所, 1982: 22-26.
XUE J C, YANG Y G. Test method for buckling deformation curve of fastener[M]. Xi'an: Aircraft Structure Strength Research Institute, 1982: 22-26. (in Chinese) |
| [21] |
薛景川, 杨玉功.
紧固件载荷变形曲线的工程确定方法[M]. 西安: 飞机结构强度研究所, 1984: 23-29.
XUE J C, YANG Y G. Engineering determination method for buckling deformation curve of fastener[M]. Xi'an: Aircraft Structure Strength Research Institute, 1984: 23-29. (in Chinese) |
| [22] |
刘仁宇.某型飞机外翼下壁板连接件细节应力分析和疲劳性能研究[D].西安: 空军工程大学, 2008: 43-48.
LIU R Y.Failure analysis for lap joint panel of an outer wing in fatigue test[D].Xi'an: Air Force Engineering University, 2008: 43-48(in Chinese). |



