从移动方式上看, 移动机器人可分为轮式、履带式、腿式(单腿式、双腿式和多腿式)和水下推进式[1]。现今,各种移动机构层出不穷,灵活高效的轮式移动机器人一直被学者或研究人员保留并沿用。为了解决轮式机构越障性能不佳的问题,国内外学者纷纷提出了各种解决方案。
异形车轮由于其移动效率较高且相对于普通轮式机构有更加理想的越障性能,被广大研究者们所接受。然而其对于步态的控制仍具有较为严格的要求。为了进一步降低操作难度,兼具普通轮式和异形车轮外形的变形车轮逐渐进入人们的视野。同时,为了满足变形要求,车轮本身的驱动也逐渐复杂化。国防科技大学江海波和潘存云设计了一款轮体内部由行星齿轮系驱动的移动机器人[2],与常见轮式机器人相比具有大扭矩和可改变越障高度的优势。1995年河南科技大学李水良等提出了一种圆规腿步行机构[3]。利用计算机控制,补偿了步行轮多边形效应,并适应各种坡度路面。2003年哈尔滨工业大学邓宗全等提出了行星轮式月球车[4],利用3个子轮等分布圆周阵列的特殊构型提高了越障能力。2007年北京航空航天大学岳荣刚等提出了一种新型轮爪式车轮。以机械手段优化前者思路,降低了控制难度[5]。同年,文献[6]提出的一种新型轮腿式机构“Mini-WHEGSTM”[6]成为了步行轮中解决刚性路面越障问题的又一个经典构型。协同以步态规划模仿蟑螂的运动,能以较快的行进速度翻越较大高度的硬路路障。西南大学葛耿育设计的偏心轮腿六足机器人(Eccentric-type Legged Hexapod Robot, ELHR)[7]则以六足偏心轮腿,将普通圆轮的输出轴偏置以提高其极限越障高度。吉林工业大学陈德兴等提出了利用偏心轮机构[8],实现轮腿伸缩的机械传动式步行轮。通过腿的伸缩保证车轮在跨步行驶过程中轮心的离地高度基本不变。既提供了较大的牵引力,又在一定程度上提高了车辆的行驶平顺性。2001年美国JPL(Jet Propulsion Laboratory)提出了可膨胀轮[9], 2007年LRP(Laboratoire de Robotique de Paris)提出了一种缩放车轮[10],着重强调轮径大小变化对车轮通过能力的影响。2007—2008年北京航空航天大学孙鹏等提出了一种可变直径轮式深空概念车[11-12],通过对扩展式轮形翻越松软路面的简化模型证明了该轮形对应松软路面的有效性。
轮腿式和扩展式已经成为异形轮中步行轮的2个经典构型。然而扩展式虽在松软路面上有较强的通过能力,其对于硬路面的复杂路况通过能力则不如轮腿式。同时,轮腿式对硬路面通过能力强,但应对松软路面表现不佳。研究发现变形车轮在轮形方面的研究虽日渐成熟,但仍普遍存在对应地形种类单一的问题。对以泥泞地和极地为典型软硬兼有的复杂路况,其可通过性仍有待商榷。尚需就构型的通用性对方案作进一步研究。
本文基于加拿大拉瓦尔大学学者Gosselin和Gagnon-Lachance于2006年提出的平面多边形机构[13],对一种集轮腿式、扩展式和常规轮式为一体的单自由度变形车轮机构进行构型综合,结合锁合机构进一步提升构型有效利用率,为轮式越障机构提供了一种新的设计方法。
1 变形车轮设计过程 1.1 常见路面分类与传统变形车轮普通车轮的越障性能不佳,生活中存在以乱石堆为代表的硬路面路障和以沙地为代表的松软地形往往对轮式车辆的移动造成了极大的阻碍。除了常利用特殊胎面进行对应的光滑路面,人们也常利用轮形本身的特异性解决上述二者问题。
极限越障高度是判断越障机构对于硬路面障碍通过能力的重要指标。北京交通大学杨春于2010年基于Mini-WHEGSTM对轮腿式变形轮进行了越障分析[14]。研究表明在具有相同构型有效半径并处于相同地形环境下,轮腿式的极限越障高度约为普通轮式的1.656倍[14]。综合以机构本身在变形时产生的有效半径伸缩比,轮腿式相比于普通轮式的越障能力优化倍数将是1.656与构型有效半径伸缩比的乘积。
北京航空航天大学高峰等基于扩展式变形轮和普通轮式越障车对于松软路面的通过能力进行对比做出分析,表明车轮的展开有利于提高其挂钩牵引力,提高牵引通过性,并指出滑转率在0.2~0.3时, 车轮驱动效率达到最大值[11, 15]。
然而受制于气候等不可控因素,越障车所处实际地形与理想地形存在差距。实际地形多兼具刚性路障和松软地形。仅对传统变形车轮进行单一地形通过性的优化难以达到预期目的。对变形车轮通用性的优化研究就成为一种必然的趋势。
1.2 机构方案设计选型设计要求对松软路面和具备较大路障的刚性路面兼具良好的通过性,故将扩展式和轮腿式2种构型相结合。
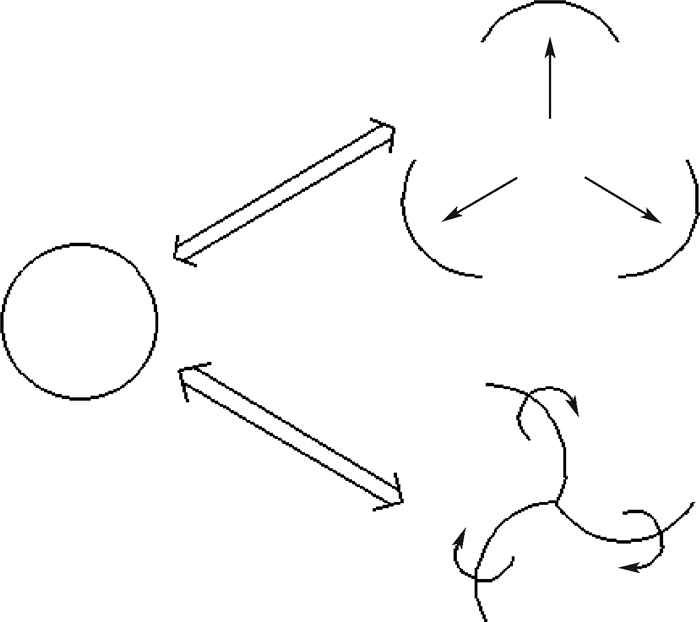
所设计构型应满足以下条件:①为使控制方便,尽可能降低机构自由度。②控制变形的电机若布置于轮体上,在车轮行进中导线将被绞断绞断。为避免此问题,将主动件安排在构型中心并与机架(车体固连)。③如图 1所示,构型应同时满足使末端执行件(轮瓣)向外扩展和翻转2种运动。
|
| 图 1 轮式机构变形要求 Fig. 1 Deformation requirement of wheel mechanism |
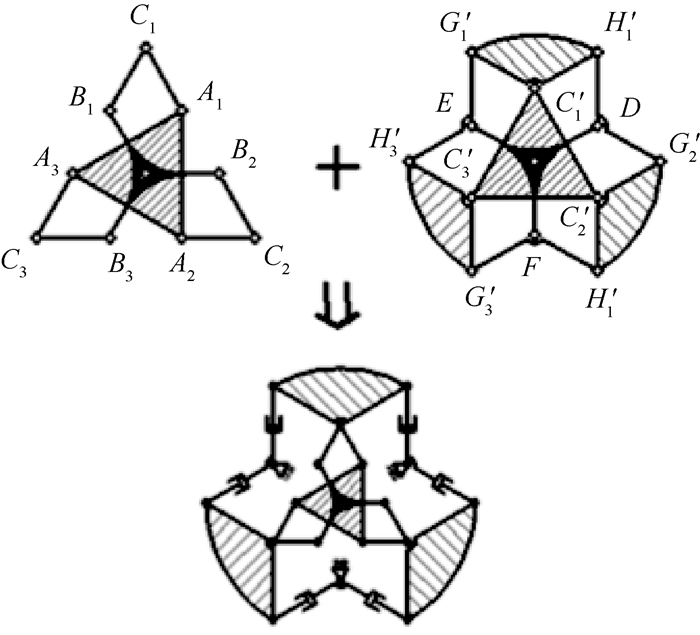
如图 2上方左侧方机构所示,扩展式与轮腿式之间的变换可以通过剪叉机构的扩展性满足伸缩要求。如图 2上方右侧机构所示,杨春提出了单自由度变形轮(8杆)[14],实现了普通轮式与轮腿式间的变换。变形轮机构相当于由单一变形机构等分布圆周阵列而成。为便于分析,将具有相同意义的铰链以同样的字母不同下标做代替,两机构在进行型综合时其代替点取相同标号并以撇号加以区分,公共铰链另起名不加下标。如图 2所示,将上方左侧机构刚化并代替中间机构的构件C1′C2′C3′取其中一个构件C1′A1′B1′及与其相连接的杆件进行分析。由机构的几何关系可知,若使上述单自由度变形轮向外扩展,连杆G1′E、H1′D将沿其长度方向伸长。将连杆G1′E、H1′D分别添加移动副使机构解除一个自由度的约束,即得到一种目标构型。目标构型中将主动件A1A2A3和主动件B1B2B3反向等速转动可实现扩展式的变形,主动件A1A2A3和主动件B1B2B3同向等速转动可实现轮腿式的变形。
|
| 图 2 多段变形轮方案1 Fig. 2 Scheme 1 for multistage transformable wheel |
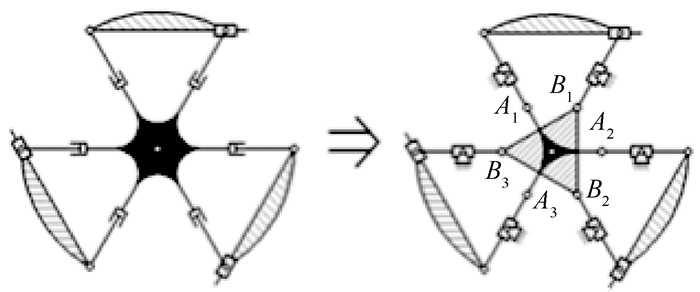
另一种思路如图 3左侧机构所示,直接在连接轮瓣的连杆上添加移动副,通过控制连杆的伸缩实现3种轮形的变换。如图 3右侧机构所示,通过等效替换降低自由度并将主动件安排至中心位置。将主动件A1A2A3和主动件B1B2B3反向等速转动可实现扩展式的变形,主动件A1A2A3和主动件B1B2B3同向差速转动可实现轮腿式的变形。
|
| 图 3 多段变形轮方案2 Fig. 3 Scheme 2 for multistage transformable wheel |
如图 4左侧机构,还可通过一自由度类天平机构实现轮式与轮腿式之间的变换。在连杆JO上增加移动副使机构增加一个自由度,如图 4右侧机构,该构型可同时满足轮式、扩展式和轮腿式的变换要求。将主动件A′1A′2A′3和主动件B′1B′2B′3反向等速转动可实现扩展式的变形,主动件A′1A′2A′3和主动件B′1B′2B′3同向差速转动可实现轮腿式的变形。

|
| 图 4 多段变形轮方案3 Fig. 4 Scheme 3 for multistage transformable wheel |
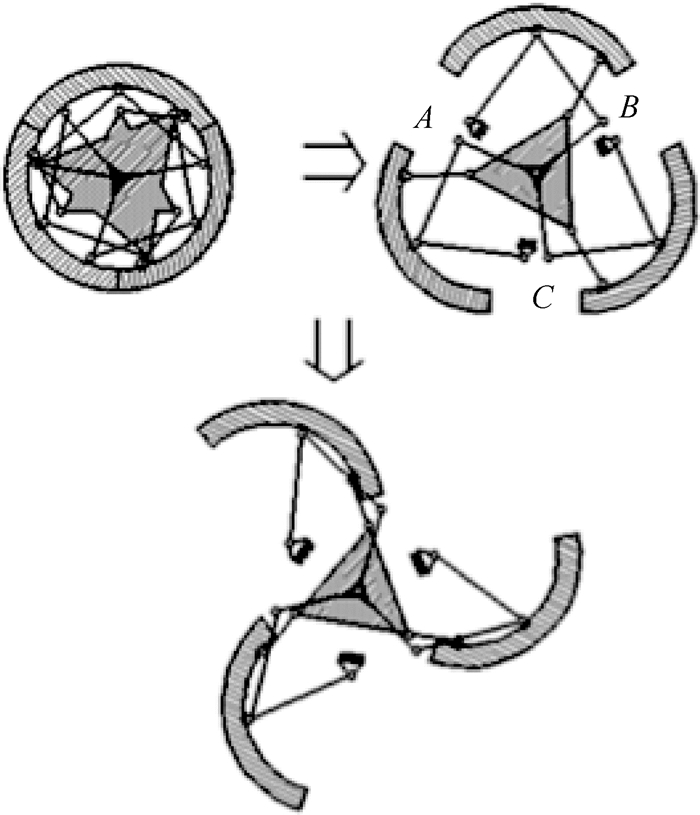
最后一种思路即利用折展机构完成轮式与轮腿式的变换并利用折展的中间轨迹满足扩展式的变形需求。如图 5所示,可利用Gosselin和Gagnon-Lachance提出的折展机构[13],将其末端构件视为一个轮瓣,通过添加一定的长度约束关系即可满足相关要求。
|
| 图 5 多段变形轮方案4 Fig. 5 Scheme 4 for multistage transformable wheel |
考虑到变形机构用于轮体,为便于控制与传动设计,应保证自由度尽可能低并将主动件向中心转化。移动副在作为从动件使用时容易因加工精度要求过高等问题致使摩擦角过小而发生自锁,设计时应注意尽可能避免或进行足够的保护。综合考虑上述因素决定采用方案4。
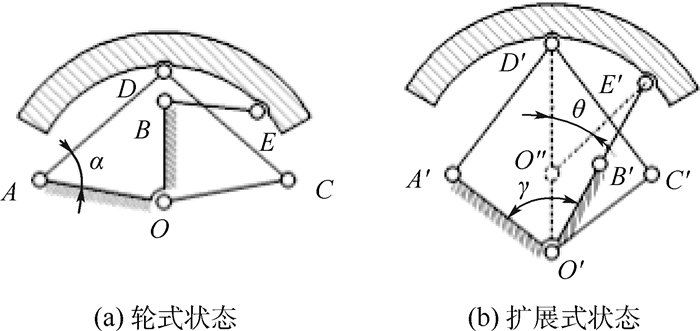
2 构型分析与优化构型存在各杆长选取的最优解问题。如图 6所示,取其中一只轮瓣进行分析,基于实验从实际出发提出如下指标:①为保证机构的可使用性,连杆AD与AO构成的压力角对于普通轮式不大于40°,轮腿式时不大于50°,扩展式时为α。②对于扩展式,使连杆E′B′和B′O′共线利用奇异位置进一步保证刚度。对于普通轮式,连杆EB和BO的压力角不大于50°。③为避免理论模型与实际轮体因干涉等问题出现过大误差,铰链D与E的布置点与中心铰链O的连线同轮瓣边缘的夹角不小于10°。其中在保证机构的利用率的前提下满足变形需求,α应尽可能靠近50°。
|
| 图 6 杆长分析 Fig. 6 Analysis of link length |
铰链D与E的距离越小,构型在由普通轮式变换至轮腿式时的伸缩比越大。铰链D与E的距离越远,构型在由普通轮式变换至扩展式时的伸缩比越大。为寻找铰链D与E的最优间距,将铰链D的位置作为变量,其余指标取极限值作为约束条件,同时为使构型伸缩比有最大值,易知轮式状态下铰链D与O的连线长度
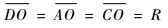
|
(1) |
式中:R为设计变形轮在普通轮式状态下的内圆半径。利用普通轮式的内部连杆几何状态可得到连杆之间存在如下关系:
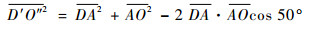
|
(2) |
如图 6所示,将扩展轮式中铰链D′与E′分别与O″连线所夹角度设为θ,由轮式提出的条件知

|
(3) |
式中:
在扩展式中:
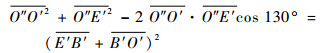
|
(4) |
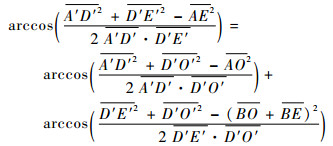
|
(5) |
式中:
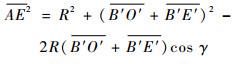
|
又有
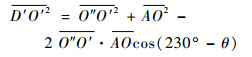
|
(6) |
联立式(1) ~式(6)即可解出构型内部所有杆长与R、α和θ间的关系。
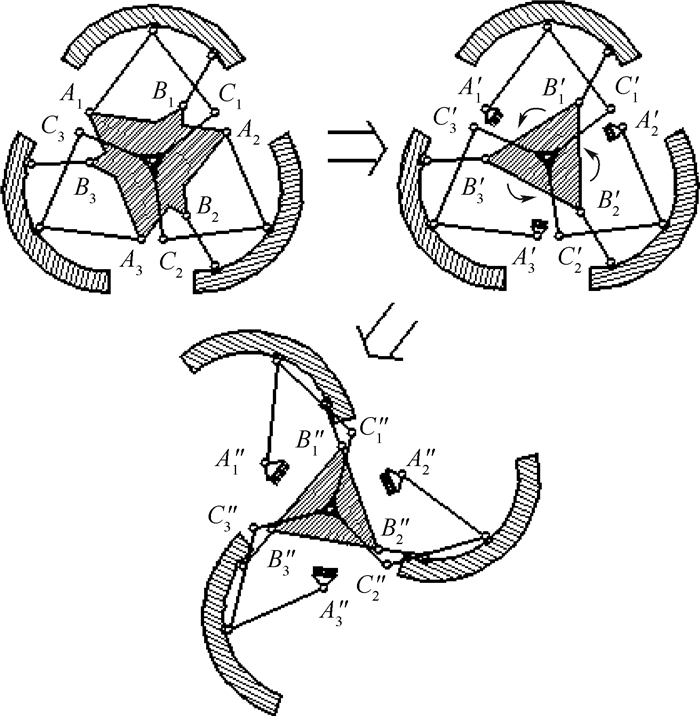
上述方法所设计的连杆长度关系已满足扩展式和普通轮式之间的变形要求。然而满足上述关系的构型在进一步向轮腿式变形时,连杆EB和BO可能因长度不足导致机构无法运动至目标位置。提出如下2种解决方案:①与目标位置相差较小的情况下,微调连杆EB和BO的长度使构型在各工作状态下压力角皆处于误差内。②与目标位置相差较大的情况下,如图 7所示,通过锁合机构与限位机构使原本固连的构件A1A2A3和B1B2B3松开并独立。将构件C1C2C3作为主动件使机构由扩展式向轮腿式变化的过程中,构件B1B2B3受连杆固有长度影响,被动地牵拉至新的位置,并由限位机构限制其进一步转动。
|
| 图 7 锁合机构工作原理 Fig. 7 Working principle of lock mechanism |
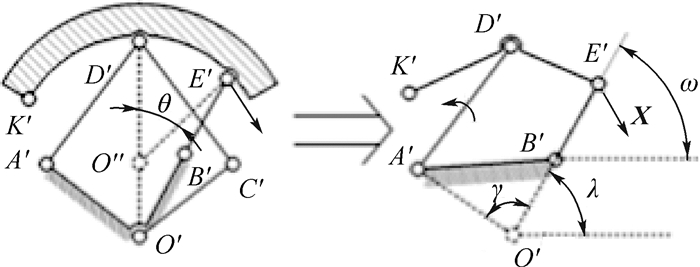
如图 8所示,向量X为轮瓣边缘的切线。轮瓣已变形至轮腿式要求位置即满足向量X与直线E′O′重合。将当前状态下连杆E′O′与X的夹角视为正值。则锁合机构的使用与否取决于在扩展式状态下,连杆A′D′逆时针旋转至死点位置时,A′D′与A′O′的夹角是否小于140°。此时可能出现4种结果:①机构可达到目标位置,且E′O′与X的夹角为正值。此为由扩展式变形至轮腿式时伸缩比过小所致。该情况无需使用锁合机构但应将θ调小或适当调小扩展式中A′D′与A′O′的夹角α。②机构可达到目标位置,且E′O′与X的夹角为负值。此为由扩展式变形至轮腿式时伸缩比过大所致,该情况下无需使用锁合机构但应适当增大扩展式时A′D′与A′O′的夹角α或将θ增大。③机构可达到目标位置,E′O′与X的夹角等于0°,此时连杆满足使用要求,无需添加锁合机构。④机构先到达死点,不能到达目标位置。该情况下需要使用锁合机构。
|
| 图 8 变形分析 Fig. 8 Analysis of transformational motion |
在无需加入锁合机构的前提下,以O′为参考点,对机构的各点坐标进行分析。
A′的坐标为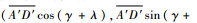


|
处于扩展式时,D′1的坐标为(Rcos(γ+λ)+ 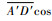
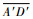
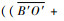
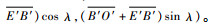
处于轮腿式时,D′2的坐标为
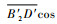
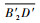
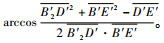
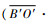
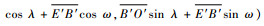
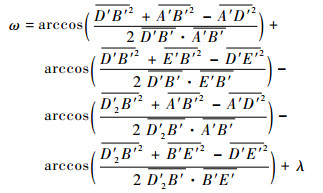
|
(7) |
其中:
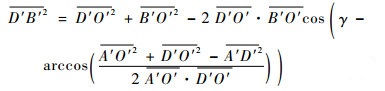
|
(8) |
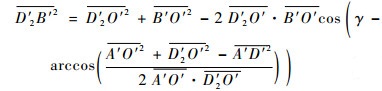
|
(9) |
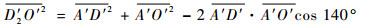
|
(10) |
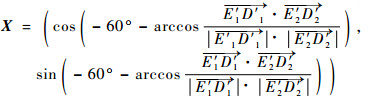
|
(11) |
机构处于轮腿式时有

|
(12) |
四杆机构在到达死点位置时,D′A′与A′O′夹角为

|
(13) |
其中:
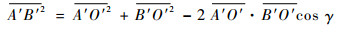
|
(14) |
式(13)、式(14)可作为是否加入锁合机构的判断依据。此时,若β的变化量Δβ<50°-α则需要加入锁合机构,若Δβ>50°-α则无需加入锁合机构。
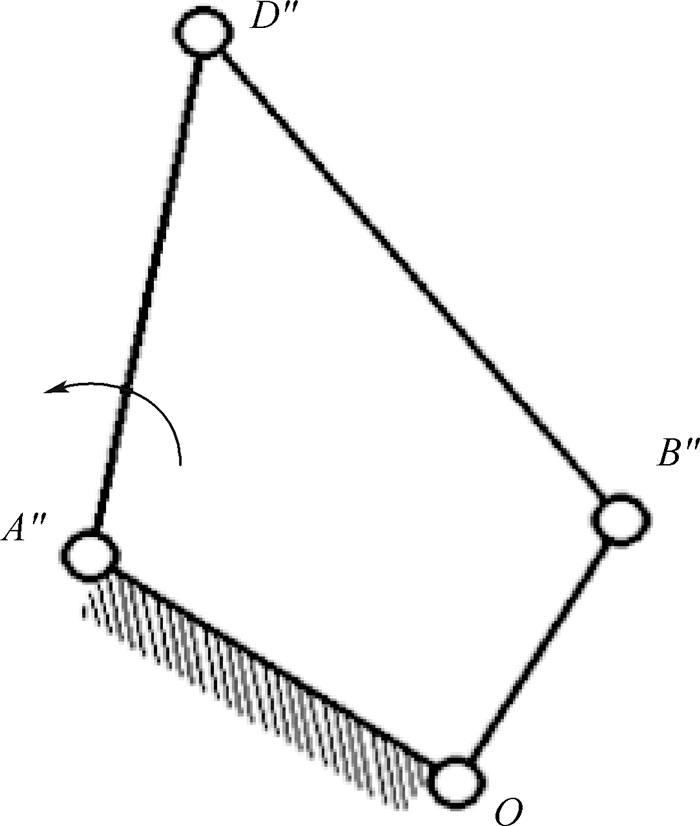
在需要使用锁合机构的前提下,如图 9所示,此时机构可等效为四杆机构。
|
| 图 9 锁合机构分析 Fig. 9 Analysis of lock mechanism |
实际在设计锁合机构时,为避免机构因奇异位置而锁死,在铰链E′处常加一个简易的限位机构使得D′E′与E′B′无法共线,但一般D′E′与E′B′仍接近共线状态,影响量较小故忽略不计。
此时利用式(11)、式(12),式中以B′点取代E′,可反推出点B′的坐标,进而求解出A′O′与B′O′的新夹角γ2与新的E″点。
扩展式半径R1为
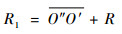
|
(15) |
轮腿式半径R2为
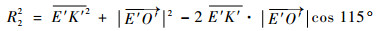
|
(16) |
式中:点K′为轮瓣变换为轮腿式时的最远点。

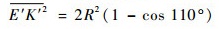
|
(17) |
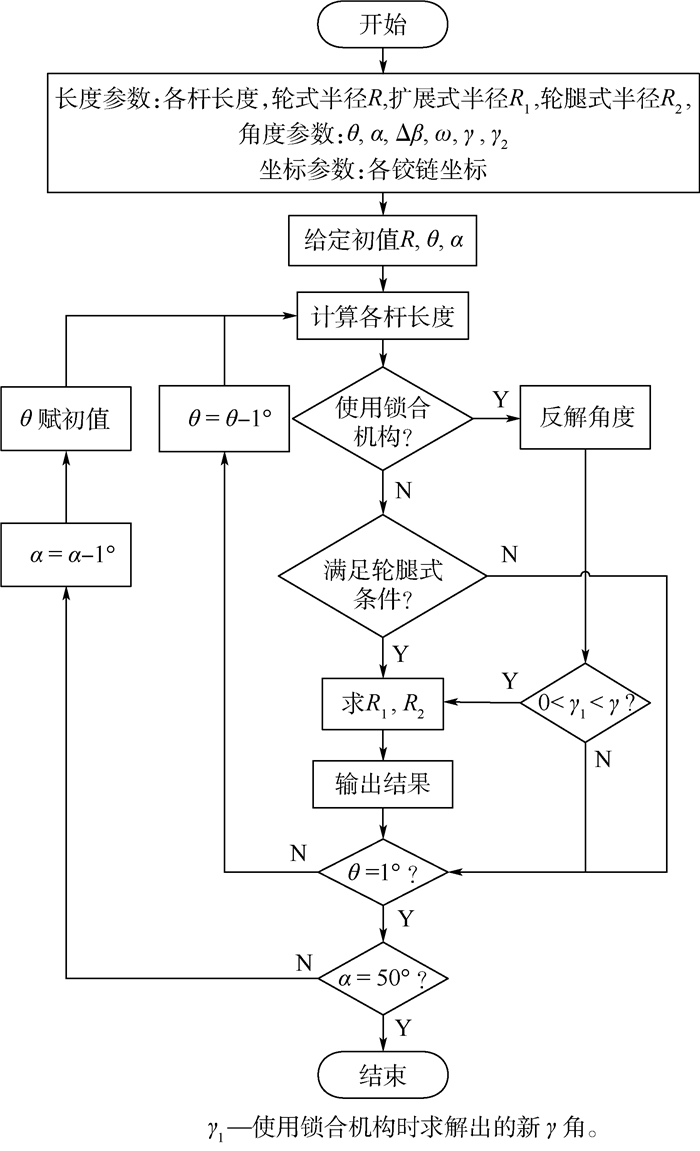
利用MATLAB将式(1)~式(17)联立即可求出多组解,取其中轮腿式半径R2与扩展式半径R1较大者为优。以1°为分度,对于轮腿式的扩展角度提供±5°的容差。其流程如图 10所示。
|
| 图 10 MATLAB流程图 Fig. 10 Flowchart for MATLAB |
θ的值随着α的增大而减小。使用锁合机构即在θ不变的情况下进一步减小α值,设计中没用使用的必要。图 11为不使用锁合机构的前提下R1/R、R2/R与α的变化趋势图。数据表明,构型扩展式的伸缩比随着α的增大而增大;轮腿式的伸缩比随随α的增大而增大。根据数据显示,理论上θ最小可达19°,此时,R1≈2.099R,R2≈ 2.929R。考虑结构的刚度问题,θ不宜取过小,最终选择:α=20°, AO=R, AD≈0.286R, BO≈0.798R, BE≈0.910R。此时θ=42°, R1≈1.884R, R2≈2.660R。无需使用锁合机构。

|
| 图 11 R1/R、R2/R与α的关系 Fig. 11 Relationship between R1/R, R2/R and α |
如图 12和图 13所示,将所设计的多段式变形轮进行仿真建模后最终完成实际制作。轮体由2组行星齿轮系并列而成。分别对行星架和太阳轮进行控制,利用行星齿轮组任意2个主动件对输出方成一定比例叠加的特性,满足变形轮转动时轮体两中心部件(对应图 7杆件A′O′B′和杆件C′O′)同步转动和变形时轮体两中心部件的差速转动要求。

|
| 图 12 Solidworks零件模型 Fig. 12 Part models designed by Solidworks |

|
| 图 13 搭载多段变形轮的移动机器人 Fig. 13 Mobile robot with multistage transformable wheels |
1) 根据现有的几种简易机构进行型综合,提出了4种多段式变形车轮机构。
2) 对上述机构中的较优方案进行了构型分析与杆长优化,得到了适合轮式无人越障车辆的机构。
3) 根据数据分析,构型利用率随变形轮处于扩展式时压力角α的增大而增大。即不添加锁合机构的情况下构型随θ的减小而增大。同时,构型利用率受材料强度和刚度和实际机构装配情况制约。达到理论极限时扩展式有效半径约为轮式半径的2.099倍,轮腿式有效半径约为轮式半径的2.929倍。
| [1] |
徐国华, 谭民. 移动机器人的发展现状及其趋势[J].
机器人技术与应用, 2001 (3): 7–14.
XU G H, TAN M. The current situation and tendency of mobile robots[J]. Robot Technique and Application, 2001 (3): 7–14. DOI:10.3969/j.issn.1004-6437.2001.03.003 (in Chinese) |
| [2] |
江海波, 潘存云. 基于行星轮系的移动机器人及其特性分析[J].
机械制造, 2005, 43 (12): 11–13.
JIANG H B, PAN C Y. Analysis of mobile robot based on planetary gear train and its characteristics[J]. Machinery, 2005, 43 (12): 11–13. DOI:10.3969/j.issn.1000-4998.2005.12.003 (in Chinese) |
| [3] |
李水良, 魏道付, 高峰, 等. 步行轮机构及运动控制方案[J].
洛阳工学院学报, 1995, 16 (1): 63–68.
LI S L, WEI D F, GAO F, et al. The mechanisms and motion control of the terrain-adaptive walking wheel[J]. Journal of Luoyang Institute of Technology, 1995, 16 (1): 63–68. (in Chinese) |
| [4] |
邓宗全, 高海波, 胡明, 等. 行星越障轮式月球车的设计[J].
哈尔滨工业大学学报, 2003, 35 (2): 203–206.
DENG Z Q, GAO H B, HU M, et al. Design of lunar rover with planetary wheel for surmount obstacle[J]. Journal of Harbin Institute of Technology, 2003, 35 (2): 203–206. DOI:10.3321/j.issn:0367-6234.2003.02.018 (in Chinese) |
| [5] |
岳荣刚, 王少萍, 焦宗夏, 等. 一种新型轮爪式车轮设计与性能仿真[J].
北京航空航天大学学报, 2007, 33 (12): 1408–1411.
YUE R G, WANG S P, JIAO Z X, et al. Design and performance simulation of a new type wheel with claws[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33 (12): 1408–1411. DOI:10.3969/j.issn.1001-5965.2007.12.007 (in Chinese) |
| [6] | HORCHLER A D, QUINN R D, LAMBRECHT B, et al. Highly mobile robots that run and jump: US7249640[P]. 2007-07-31. http://www.freepatentsonline.com/7249640.html |
| [7] |
葛耿育. 基于异形轮组合的小型机器人越障性能研究[D]. 重庆: 西南大学, 2014.
GE G Y. Research on obstacle properties of smallrobot based on abnormal wheels[D]. Chongqing: Southwest University, 2014(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10635-1014261643.htm |
| [8] |
陈德兴, 陈秉聪, 张书军. 步行轮机构原理[J].
农业工程学报, 1994, 10 (2): 123–129.
CHEN D X, CHEN B C, ZHANG S J. The principle of walking wheel mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering, 1994, 10 (2): 123–129. (in Chinese) |
| [9] | JONES J A. Inflatable robotics for planetary applications[C]//Proceedings of 6th International Symposium on Artificial Intelligence, Robotics, and Automation in Space: A New Space Odyssey. Pasadena: Jet Propulsion Laboratory, NASA, 2001: 1-6. https://ntrs.nasa.gov/search.jsp |
| [10] | GRAND C, BIDAUD P, JARRASS É N. Innovative concept of unfoldable wheel with an active contact adaptation mechanism[C]//Proceedings of 12th World Congress in Mechanism and Machine Science(IFToMM), 2007: 1225-1232. https://www.mendeley.com/research-papers/innovative-concept-unfoldable-wheel-active-contact-adaptation-mechanism/ |
| [11] |
孙鹏, 高峰, 李雯, 等. 深空探测车可变直径车轮牵引通过性分析[J].
北京航空航天大学学报, 2007, 33 (12): 1404–1407.
SUN P, GAO F, LI W, et al. Analysis of traction traffic ability of diameter variable wheel for planetary rover[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33 (12): 1404–1407. DOI:10.3969/j.issn.1001-5965.2007.12.006 (in Chinese) |
| [12] |
孙刚, 高峰, 孙鹏. 可变直径轮月球探测车及其越障能力分析[J].
机械设计, 2008, 25 (5): 21–23.
SUN G, GAO F, SUN P. Moon detection with diameter variable wheels and its obstacle surmounting capability analysis[J]. Journal of Machine Design, 2008, 25 (5): 21–23. (in Chinese) |
| [13] | GOSSELIN C M, GAGNON-LACHANCE D. Expandable polyhedral mechanisms based on polygonal one-degree-of-freedom faces[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2006, 220 (7): 1011–1018. DOI:10.1243/09544062JMES174 |
| [14] |
杨春. 基于变形车轮的移动机构研究[D]. 北京: 北京交通大学, 2010.
YANG C. The research of mobile mechanism based on transformable wheels[D]. Beijing: Beijing Jiaotong University, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10004-2010120108.htm |
| [15] |
解晓琳, 高峰. 适用于松软地面的可变形轮牵引特性分析[J].
农业机械学报, 2016, 47 (s1): 457–463.
XIE X L, GAO F. Tractive performance analysis of transformable wheel on soft terrain[J]. Transactions of the Chinese Society of Agricultural Machinery, 2016, 47 (s1): 457–463. (in Chinese) |



