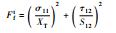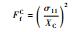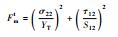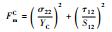轻量化是实现节能减排和解决电动汽车续驶里程不足的重要途径。实现手段包括:轻质材料替代、结构优化和先进制造及装配工艺应用。其中,轻质材料替代的轻量化效果最为显著。碳纤维增强树脂基复合材料由于具有远高于传统钢材的“比模量”和“比强度”,有望在汽车结构件上得到更广泛的应用[1]。悬架弹簧作为重要的汽车底盘结构件,其质量的减轻可降低整车的簧下质量,因此可极大提高整车的平顺性和操纵稳定性,近几年已引起国内外汽车企业的广泛关注。
2010年,Budan和Manjunatha[2]分别以碳纤维复合材料(CFRP)、玻璃纤维复合材料(GFRP)以及碳纤维/玻璃纤维(CF/GF)混合复合材料制作了3种螺旋弹簧样件,并通过台架实验证明CFRP弹簧刚度比GFRP高45%,比CF/GF高34%;同时,CFRP弹簧质量比GFRP弹簧减轻17.8%,比CF/GF混合复合材料弹簧减轻15.0%,该研究证明了弹簧材料替换的可行性。2015年,Choi等[3]用理论模型建立了连续纤维层合板弹簧中纤维方向、簧丝直径和弹簧刚度之间的关系,研究表明:当纤维铺层方向为45°时,能够在满足刚度要求的情况下使簧丝直径最小,并分别用数值仿真和实验方法对该结果进行了验证。2016年,Sequeira等[4]利用有限元法证明CFRP弹簧在仅保证与金属弹簧具有相同强度和刚度的前提下,可减重80%左右。Jang等[5]通过复合材料力学原理设计了一款复合材料螺旋弹簧,能够极大地降低弹簧质量,可在汽车上使用,但未见提及参数优化。Oh和Choi[6]研究了复合材料的力学特性,推导了其剪切模量与铺层角度的关系,并最终确定了与对标金属弹簧具有相同刚度的复合材料弹簧设计结果。通过数值仿真对其进行了验证。由于缺少结构优化环节,不能确定是否达到了最佳轻量化效果。Djomseu等[7]提出了一种螺旋弹簧的设计方法。建立螺旋弹簧有限元模型,考虑纤维铺层角度等影响因素为优化变量,通过修改变量和进行有限元仿真计算的循环过程,得到最终优化结果。然而,优化过程中每一次迭代都需要进行一次有限元仿真,且迭代次数随着优化变量的增加而增加,因此该方法计算成本大。
优化是结构设计中的重要组成部分。其中,基于响应面模型的优化方法已经成为国内外学者研究复杂几何及非线性响应的常用工具[8-9],已经广泛应用于结构设计中。Arora等[10]利用响应面模型对汽车钢板悬架弹簧的弹簧片疲劳特性进行了优化。考虑了弹簧片跨距和宽度等几何参数,以及材料强度、弹簧刚度和强度缩减系数等5个因素对疲劳特性的影响,且响应面模型的预测精度通过实验得到了验证。基于响应面模型寻优,得到了提高疲劳寿命的最优方案。
根据上述复合材料螺旋弹簧的研究现状,本文结合复合材料力学原理和有限元仿真法,提出了一种汽车复合材料螺旋弹簧从理论设计、仿真校核到结构优化的完整设计流程,为工程开发提供理论和方法指导。以某款面包车为例,依据所提出的设计要求,应用该方法设计了一款复合材料螺旋弹簧。首先,针对弹簧载荷特点和主要失效模式,选择了合适的材料和铺层方式,进行了初始结构参数设计;然后,建立了数值仿真模型,并验证了初始设计结果;接着,利用正交实验设计和数值结果建立了弹簧几何结构与刚度、强度的映射关系,并构建了响应面模型;最终,基于响应面模型对初始设计参数进行优化,极大地提高了设计质量和效率。
1 设计参数初值的理论推导应用复合材料力学原理,可以得到比较合理的、用于后续优化的设计变量初值,能够减少获得全局最优解所需的迭代次数。
1.1 强度和刚度理论模型本节关于复合材料圆柱螺旋弹簧的压缩强度和刚度理论模型的推导,基于以下假设:
1) 所有变形均为小变形,且在线弹性范围内。
2) 簧丝截面为圆形且在面内保持不变。
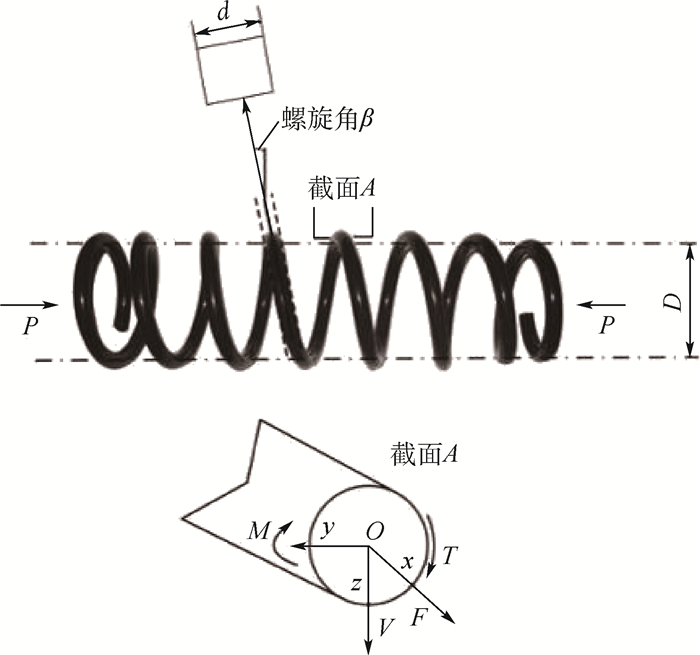
弹簧在轴向压缩载荷P作用下,任意截面的受力情况如图 1所示。
|
| 图 1 弹簧及簧丝截面受力情况 Fig. 1 Force analysis of spring and cross section of wire |
截面A-A受到4个分力(力矩)作用,分别为垂直于横截面的纵向(z向)剪切力V、沿簧丝切向(x向)的拉力F、绕簧丝截面法向(x轴)的扭矩T和沿y轴的弯矩M。
根据材料力学理论:当弹簧螺旋角β较小时,由其引起的弯矩M和拉力F等可忽略;当弹簧旋绕比C较大,即C=D/d≥10时(D和d分别为弹簧中径和簧丝直径,定义见图 1),剪切力V对弹簧压缩刚度贡献较小,也可忽略。因此,经典解析解中,满足上述条件的弹簧一般仅考虑簧丝所受扭矩T,忽略其他3个作用力及力矩[11]。基于上述假设,本文的理论模型推导如下:
在轴向载荷P作用下,螺旋弹簧刚度κ为
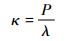
|
(1) |
式中:λ为载荷P引起的变形,其计算式为
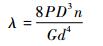
|
(2) |
式中:n为有效圈数;G为弹簧材料的剪切模量。
由式(1)和式(2)可知:以塑代钢时,弹簧刚度除了与几何尺寸有关外,还受复合材料在截面上的剪切模量影响。
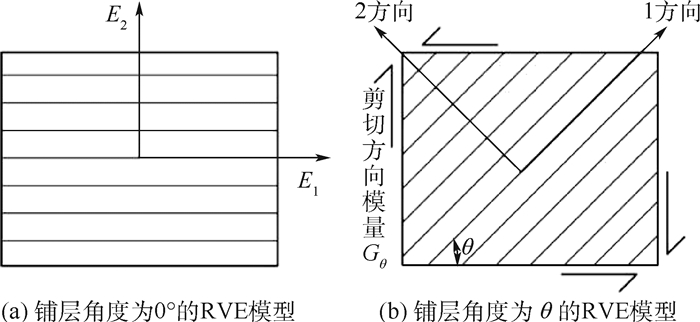
图 2为复合材料单层的代表性体积单元(RVE)示意图。本文采用的材料参数列于表 1[12]。其中,E1为单层层合板纤维方向的弹性模量,E2为单层层合板垂直纤维方向的弹性模量,G12为单层层合板垂直线方向的剪切模量,ν12为泊松比,XT为纤维拉伸强度,XC为纤维压缩强度,YT为基体拉伸强度,YC为基体压缩强度,S12为单向纤维与基体混合后的单向层合板横向剪切强度(纤维方向为纵向)。当铺层顺序为±45°时,材料的许用剪切强度S±45°为361.7 MPa。
|
| 图 2 RVE的铺层结构示意图 Fig. 2 Schematic of layer structure of RVE |
根据复合材料力学原理,可推导出RVE的剪切模量:

|
(3) |
式中:Ef和Em分别为纤维和基体的拉伸弹性模量。
单向复合材料的剪切模量随θ变化,在θ=45°时达到最大。因此,为了提高单层材料的剪切模量,本文采用±45°铺层。当纤维体积百分比为50%时,剪切模量的计算式为[13]
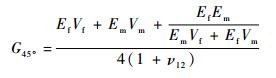
|
(4) |
式中:Vf和Vm分别为纤维和基体的体积分数。
假设纤维和基体本身均为各向同性材料。将式(2)和式(4)代入式(1),得到该复合材料螺旋弹簧压缩刚度计算式为

|
(5) |
弹簧的剪切应力τs可以由式(6)计算得到[11]:

|
(6) |
式中:Ks为弹簧圈数对强度的影响系数[3],其计算式为

|
(7) |
由于布置空间以及载荷条件的限制,某款微型面包车后悬架圆柱螺旋弹簧的设计要求[14]如下:簧丝直径为12~22 mm;弹簧中径为120~180 mm;弹簧圈数为4~10;静态压缩刚度为75 N/mm;剪切强度安全系数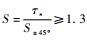
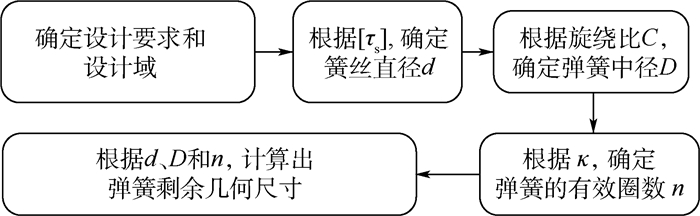
初始参数设计流程见图 3。簧丝直径根据式(8)得到:
|
| 图 3 初始参数理论设计流程 Fig. 3 Theoretical design process of inital parameters |
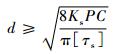
|
(8) |
按照弹簧剪切安全系数为1.3进行设计,弹簧受载时的许用剪切应力[τs]为278.2 MPa;考虑到理论模型忽略了部分力的作用,初始设计时将原本许用剪切应力再降低10%,设置为250.4 MPa。然后,根据设计所要求的压缩刚度,采用式(9)得到弹簧的有效圈数n。弹簧几何参数的初始设计结果见表 2。

|
(9) |
| 参 数 | 簧丝直径/mm | 弹簧中径/mm | 弹簧有效圈数 |
| 数 值 | 21.2 | 123.5 | 5.4 |
2 初始结构性能的有限元仿真验证
为了进一步验证第1节中的初始几何模型是否能满足设计要求,在商业有限元软件ABAQUS中建立了有限元模型并进行数值仿真。采用四面体实体单元C3D10建模。由于弹簧压缩过程中变形均匀,且通过网格尺度敏感性和收敛性检验,最终,全部单元边长均设置为5 mm。
选用Hashin失效准则[15]来判断弹簧是否发生失效,各失效机理对应的准则判据见表 3,其中,σ11和σ22分别为1和2方向上的正应力;τ12为剪应力;Fft、FfC、Fmt和FmC分别表示4种状态下失效临界值,取值均为1。
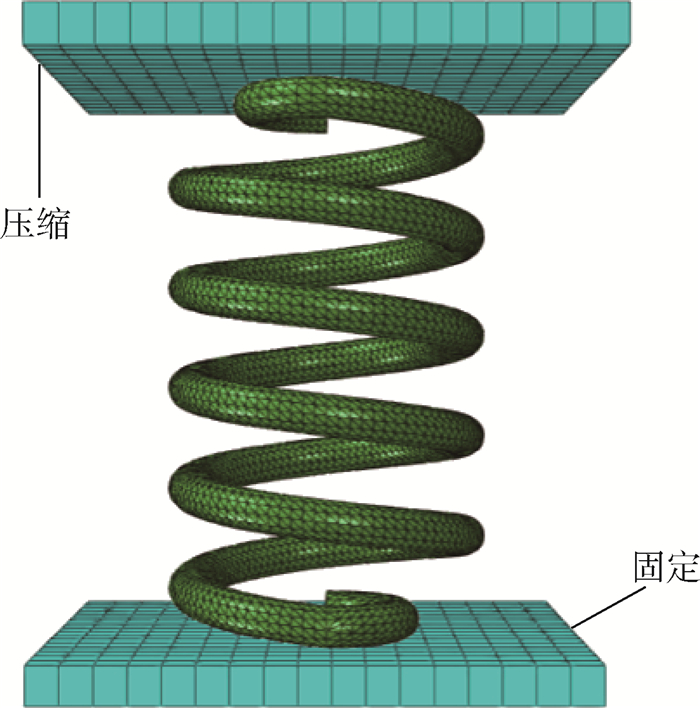
在弹簧模型的上、下两端建立2个刚性平板,与弹簧间设置为刚性接触约束,以防止穿透现象。如图 4施加边界条件和加载条件,固定下端平板,对上端平板施加向下的位移。
|
| 图 4 仿真模型中的载荷与边界条件 Fig. 4 Loads and boundary condition in simulation model |
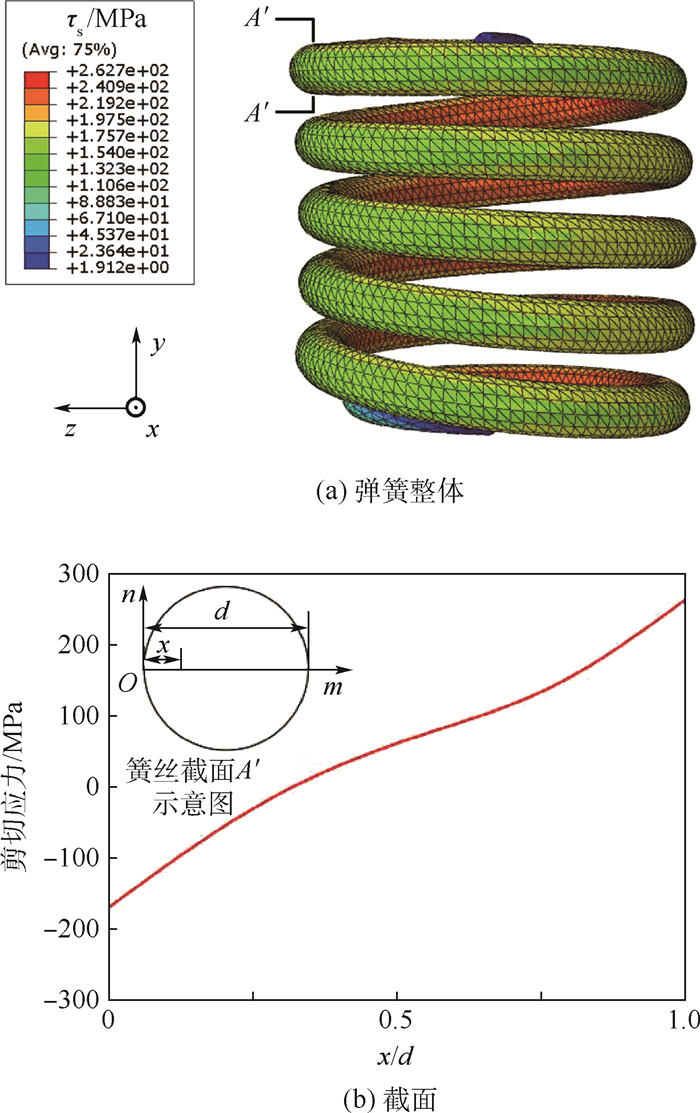
用ABAQUS/standard求解器进行静力学分析,得到压缩量达到最大值时的剪切应力τs分布结果。图 5(a)为垂直于x轴指向y轴方向上的剪切应力τs分布结果。从弹簧模型中选取一个危险截面A′,其应力分布见图 5(b),x/d为簧丝截面过圆心水平线上各点的相对位置。最大剪切应力为262.7 MPa,位于簧丝边缘处,靠近弹簧螺旋中心一端。此时弹簧的剪切安全系数为1.38,压缩刚度为73.2N/mm,均满足设计要求。因此,通过有限元仿真结果,进一步验证了理论设计得到的初始弹簧参数可满足设计要求。而且质量相比金属弹簧降低了28.5%,体现了复合材料弹簧的巨大优势。
|
| 图 5 压缩量最大时弹簧整体及截面的剪切应力分布 Fig. 5 Shear stress distribution of whole spring and cross section at ultimate compression |
然而,仿真结果也发现:最大剪切应力的数值模拟值262.7 MPa比理论设计要求的250.4 MPa略高,但是仍低于安全系数1.3要求下的剪切强度许用值278.2 MPa。此外,刚度相对于理论值也有相应的降低。这是由于在有限元仿真中,考虑到了理论计算过程中所忽略的一些力,因此最大应力会有所提高,刚度有所降低。
3 结构参数优化设计在汽车轻量化的趋势下,为了进一步降低复合材料螺旋弹簧的质量(W),本文对复合材料螺旋弹簧的几何结构进行了优化。以弹簧中径、有效圈数和簧丝直径为设计变量,以弹簧的剪切强度安全系数(S)和压缩刚度(κ)为约束条件,以重量最轻为目标,进行优化设计,数学模型如下:
优化目标:min W。
设计变量:n,D,d。
约束条件:n=4~10;d=12~22 mm;D=120~180 mm;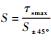
由于设计变量和约束条件较多,传统的优化过程依赖大量的有限元计算迭代次数,计算成本较高。本文采用响应面法,能够在降低计算成本的同时,保证优化结果的精度。选择具有良好连续性和可导性的二阶多项式模型,通过拉丁方正交实验设计得到了弹簧强度、刚度与弹簧中径、有效圈数和簧丝直径的映射关系,并构造了响应面模型。最终,基于响应面模型进行优化,获得满足约束条件且轻量化效果最好的复合材料弹簧几何结构。
首先,根据设计变量数目和设计域范围,选用了3因素16水平的拉丁方法进行实验设计(L16(163)),采用相同载荷及边界条件,对设计的16组样本点进行数值仿真计算,结果见表 4。
| d/mm | D/mm | n | κ | S |
| 19.27 | 120 | 5.2 | 64.94 | 1.18 |
| 20.83 | 121.06 | 6 | 84.29 | 1.33 |
| 19.66 | 122.11 | 4.93 | 66.37 | 1.22 |
| 20.05 | 123.17 | 5.87 | 71.53 | 1.26 |
| 20.44 | 124.23 | 4.13 | 68.57 | 1.27 |
| 20.25 | 125.28 | 4.53 | 72.13 | 1.29 |
| 19.08 | 126.34 | 5.47 | 61.8 | 1.31 |
| 19.86 | 127.4 | 4.8 | 55.5 | 1.14 |
| 21.03 | 128.45 | 4.67 | 74.13 | 1.38 |
| 21.22 | 129.51 | 5.33 | 75.59 | 1.39 |
| 20.64 | 130.57 | 5.07 | 80.87 | 1.38 |
| 21.81 | 131.62 | 5.73 | 66.42 | 1.29 |
| 22 | 132.68 | 5.6 | 81.3 | 1.40 |
| 21.42 | 133.74 | 4.27 | 70.64 | 1.35 |
| 19.47 | 134.79 | 4.4 | 48 | 1.29 |
| 21.61 | 135.85 | 4 | 69.81 | 1.41 |
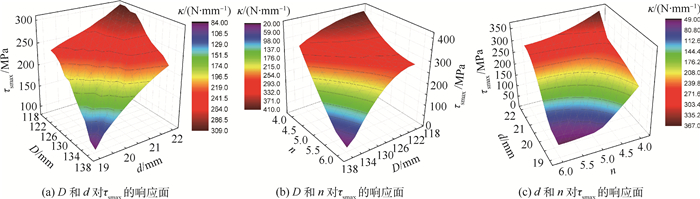
基于仿真结果,构造了响应面模型。图 6和图 7反映了3个设计变量交互作用对弹簧刚度和最大剪切应力的影响规律。图 6(a)和图 7(a)分别为弹簧刚度和最大剪切应力关于弹簧中径D和簧丝直径d的变化关系,发现当D=120 mm、d=22 mm时,弹簧刚度值为141.7 N/mm,最大剪切应力为308.8 MPa,且刚度和最大剪切应力随着弹簧中径的增大而减小、随着簧丝直径的减小而减小;同时,结合分析图 6(b)和(c)、图 7(b)和(c)可以发现,当弹簧中径D增加,另外2个变量保持不变时,弹簧刚度和最大剪切应力不断减小;当簧丝直径d增加,另外2个变量保持不变时,弹簧刚度和最大剪切应力不断增加;当有效圈数n增加,另外2个变量保持不变时,弹簧刚度和最大剪切应力不断减小。弹簧刚度和最大剪切应力随几何参数的变化趋势与理论一致。

|
| 图 6 κ与d、D和n的响应面 Fig. 6 Response surface of κ with geometric parameters d, D and n |
|
| 图 7 τsmax与d、D和n的响应面 Fig. 7 Response surface of τsmax with geometric parameters d, D and n |
然后,借助响应面模型,在设计域范围内,采用遗传算法进行优化计算。遗传算法利用简单的编码技术和繁殖机制来表现复杂的现象,可以解决非常困难的问题。首先,随机生成多个个体,形成初始群体,计算个体适应度;然后, 将各个个体适应度大小排序;再次,用各个体等级作为选择权重选取2个双亲,经杂交、突变繁殖一个后代;最后,用后代代替群体中等级最低的一个个体[16]。
最后,考虑到弹簧的制造工艺限制,经圆整后得到了最终的优化结果。表 5对比了优化前后的复合材料弹簧和金属弹簧三者之间的性能。从表 5中可以发现:在刚度和强度都能符合设计要求的前提下,优化后的复合材料弹簧的质量为3.43 kg,比优化前质量减轻了8.3%,比金属弹簧的质量减轻了34.4%。说明优化后的弹簧能够在保证设计要求的同时,进一步降低汽车质量,从而达到汽车轻量化的目标。
| 弹簧 | W/kg | κ/(N·mm-1) | S | d/mm | D/mm | n |
| 金属弹簧 | 5.23 | 75 | 2.74 | 16.4 | 142.1 | 7.3 |
| 初始理论设计复合材料弹簧 | 3.74 | 73.2 | 1.38 | 21.2 | 123.5 | 5.4 |
| 有限元优化后的复合材料弹簧 | 3.43 | 75 | 1.33 | 19.1 | 121.4 | 5.0 |
为了验证基于响应面模型优化结果的精度,根据优化结果的几何尺寸,建立新的有限元仿真。表 6为对仿真结果和响应面优化结果的比较,通过仿真得到优化后结构的最大切应力和刚度值,分别为276.4 MPa和72.7 N/mm,与响应面计算得到的结果误差分别为2.2%和3.1%,在工程误差范围内。这说明基于响应面模型得到的优化结果精准可靠。
| 约束参数 | 优化结果 | 优化结构的数值仿真 | 误差/% |
| κ | 75 | 72.7 | 3.1 |
| τsmax | 270.3 | 276.4 | 2.2 |
4 结论
本文基于汽车轻量化的大背景,为了实现以塑代钢,首先根据某车型悬架螺旋弹簧的设计要求,通过解析法推导了±45°铺层结构复合材料螺旋弹簧的初始设计参数;然后建立了相应的数值仿真模型,校验了理论设计结果;最后,以理论设计结果为初始变量,基于响应面模型对螺旋弹簧进行了几何参数优化,达到了降低弹簧质量的目标。得到以下结论:
1) 建立了复合材料螺旋弹簧设计开发流程:利用材料力学和弹性力学原理,建立了螺旋弹簧刚度和强度的简化计算公式;推导了±45°铺层复合材料螺旋弹簧的压缩刚度;按照刚度和强度指标,进行了几何参数的初步设计;应用有限元仿真法获得了具有各向异性特征的弹簧整体及界面应力分布和最大应力值;以有限元模型为依据,建立了几何参数与弹簧性能的响应面模型;基于该响应面模型进行优化,得到了满足设计要求的轻量化效果最好的复合材料螺旋弹簧结构。
2) 通过拉丁方法实验设计确定了16组样本点,建立了响应面模型。基于响应面模型,利用遗传算法,得到了最终的优化结果。最终得到的复合材料弹簧,相比原金属弹簧质量减轻达34.4%。本文提出的材料-结构-性能一体化设计流程,对其他汽车复合材料结构件的开发也有借鉴作用。
| [1] |
张靠民, 李敏, 顾轶卓, 等. 先进复合材料从飞机转向汽车应用的关键技术[J].
中国材料进展, 2013, 32 (11): 685–695.
ZHANG K M, LI M, GU Y Z, et al. Key technology of advanced composite materials from aircraft to automobile[J]. Materials China, 2013, 32 (11): 685–695. (in Chinese) |
| [2] | BUDAN D A, MANJUNATHA T S. Investigation on the feasibility of composite coil spring for automotive applications[J]. World Academy of Science Engineering & Technology, 2010, 4 (10): 1035–1039. |
| [3] | CHOI B L, CHOI B H. Numerical method for optimizing design variables of carbon-fiber-reinforced epoxy composite coil springs[J]. Composites Part B Engineering, 2015, 82 : 42–49. DOI:10.1016/j.compositesb.2015.08.005 |
| [4] | SEQUEIRA A A, SINGH R K, SHETTI G K. Comparative analysis of helical steel springs with composite springs using finite element method[J]. Journal of Mechanical Engineering and Automation, 2016, 6 (5A): 63–70. |
| [5] | JANG D, JANG S. Development of a lightweight CFRP coil spring[C]//SAE 2014 World Congress & Exhibition, 2014. https://www.sae.org/publications/technical-papers/content/2014-01-1057/ |
| [6] | OH S H, CHOI B L. A determination of design parameters for application of composite coil spring in a passenger vehicle[J]. Journal of the Korean Society of Manufacturing Process Engineers, 2013, 12 (1): 77–83. |
| [7] | DJOMSEU P, SARDOU M A, BERG T R. Composite coil spring development and testing[C]//IEEE/ASME/ASCE 2008 Joint Rail Conference. Piscataway, NJ: IEEE Press, 2008: 71-78. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1630839 |
| [8] | WANG G G. Adaptive response surface method using inherited Latin hypercube design points[J]. Journal of Mechanical Design, 2003, 125 (2): 210–220. DOI:10.1115/1.1561044 |
| [9] |
宁方飞, 刘晓嘉. 一种新的响应面模型及其在轴流压气机叶型气动优化中的应用[J].
航空学报, 2007, 28 (4): 813–820.
NING F F, LIU X J. New response surface model and its applications in aerodynamic optimization of axial compressor blade profile[J]. Acta Aeroautica et Astronautica Sinica, 2007, 28 (4): 813–820. (in Chinese) |
| [10] | ARORA V K, BHUSHAN G, AGGARWAL M L. Enhancement of fatigue life of multi-leaf spring by parameter optimization using RSM[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2017, 39 (4): 1333–1349. |
| [11] |
杨永宝, 金达锋, 高希. CFRP圆柱螺旋弹簧静刚度预测理论及仿真[J].
汽车技术, 2013 (7): 21–25.
YANG Y B, JIN D F, GAO X. Static stiffness prediction theory and simulation of CFRP cylindrical coil spring[J]. Automobile Technology, 2013 (7): 21–25. (in Chinese) |
| [12] |
朱建辉, 曾建江, 陈滨琦, 等. 复合材料层合板压缩载荷下渐进损伤分析与试验验证[J].
机械科学与技术, 2015, 34 (5): 785–789.
ZHU J H, ZENG J J, CHEN B Q, et al. Analysis and experimental validation of the progressive damage for laminate composite under compression[J]. Mechanical Science & Technology for Aerospace Engineering, 2015, 34 (5): 785–789. (in Chinese) |
| [13] |
沈观林, 胡更开, 刘彬.
复合材料力学[M]. 北京: 清华大学出版社, 2013: 231-237.
SHEN G L, HU G K, LIU B. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2013: 231-237. (in Chinese) |
| [14] |
时培成, 龚建成. 汽车悬架变刚度螺旋弹簧最优化设计[J].
现代制造工程, 2006 (11): 112–114.
SHI P C, GONG J C. Optimal design for the variable stiffness coil spring of vehicle suspension[J]. Modern Manufacturing Engineering, 2006 (11): 112–114. DOI:10.3969/j.issn.1671-3133.2006.11.037 (in Chinese) |
| [15] | ZHAN B W, SUN L Y, HUANG B C. Energy absorption optimization of GFRP Laminate by considering inner-lamina damage model with parameter identification[C]//ASME 2016 International Mechanical Engineering Congress and Exposition. New York: ASME, 2016, 11: 65774. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=2602830 |
| [16] |
徐小力, 徐洪安, 王少红. 旋转机械的遗传算法优化神经网络预测模型[J].
机械工程学报, 2003, 39 (2): 140–144.
XU X L, XU H A, WANG S H. Predicting model of the neural network with adaptation based on GA optimization to rotary machinery[J]. Chinese Journal of Mechanical Engineering, 2003, 39 (2): 140–144. (in Chinese) |