2. 江西理工大学 信息工程学院, 赣州 341000
2. School of Information Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
移动机器人自主轨迹跟踪控制的关键即为机器人在环境中的精确定位。在室外宽阔环境中, 基于GPS与惯性测量单元(Inertial Measurement Unit, IMU)融合的自主导航系统研究已经较为成熟[1-2], 尤其近年来随着人工智能(Artificial Intelligence, AI)的快速发展, 已经将深度学习用于车辆在复杂、动态环境中提高GPS定位精度[3]。在室内或GPS信号受到抑制的环境中进行导航, 研究较多的是机器人同时定位与地图构建(Simultaneous Localization and Mapping, SLAM)算法[4-5], 尤其基于激光、视觉的SLAM算法得到快速发展[6-8]。近年来也引入了基于深度学习的SLAM算法, 虽有发展, 但远没有达到实际应用的程度[9-10]。
上述室内定位算法都只是提供了机器人的局部坐标, 当转换到全局坐标时, 由于IMU的累计误差, 以及运动对传感器测量数据的影响等因素, 会出现测量精度不够等情况, 特别是当基于多机器人系统时, 算法的复杂度又大幅度提升, 实时性也受到影响[4]。不同于视觉、超声波和激光等传感器, 本文采用的超宽带(Ultra Wideband, UWB)技术可以穿透墙壁和森林, 其相较于传统窄带射频信号, 响应频率可以达到20 Hz以上, 时间分辨率高, 抗多径效应能力强, 穿透能力强, 有利于在室内完成对机器人的实时定位[11]。文献[12]提出了基于UWB的微型四旋翼自主飞行算法, 但未对UWB数据进行处理, 飞机在悬停时抖动比较剧烈[12]。张一淳等提出了基于运动学模型的室内全向机器人轨迹跟踪算法, 但未考虑机器人的动力学模型, 且没有外部定位系统, 未对位置闭环控制进行验证[13]。
本文以微型飞行器crazyflie2.0[14]与全向机器人[15]为基础, 研究了基于UWB的机器人轨迹跟踪控制算法, 并完成了轨迹跟踪、协同控制等实验, 在实际环境中验证了UWB定位系统和控制算法的实时性和稳定性。
1 超宽带定位系统以DecaWave公司最新推出的UWB测距芯片DW1000为基础[16], 构建了4个锚点、多标签的实时定位系统。
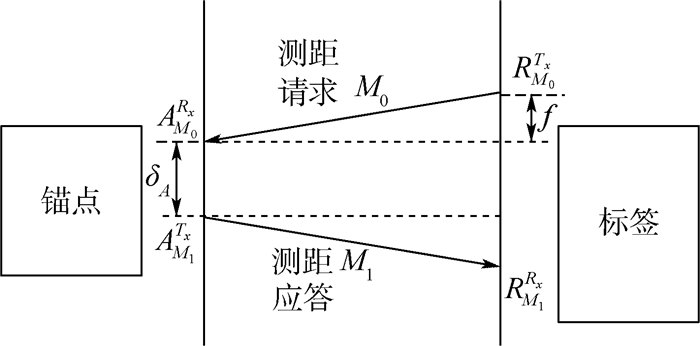
1.1 双向测距算法在锚点和标签上都装上接收机和发射机, 通过双向测距可以消除时钟误差和偏移误差, 得到更加精确的测距结果, 其算法如图 1所示。
|
| 图 1 双向测距算法 Fig. 1 Two-way ranging algorithm |
标签置于机器人上, 由标签向锚点发送测距请求, 锚点在接收到请求信号M0后, 会自动发送应答信号M1。如图 1所示, 可以看出, 2个UWB模块不是对称的。当位于机器人上的标签在RM0Tx发出请求信号M0, 锚点在延迟f时间后于AM0Rx时刻接收到脉冲。在δA时间内, 计算前沿偏移误差, 然后锚点在AM1Tx发送应答信号, 标签在延迟f时间后于RM1Rx时刻收到应答信号。则标签与锚点之间的传输时间f, 可以表示为

|
(1) |
则标签与锚点之间的距离为
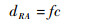
|
(2) |
式中:c=3×108 m/s为电磁波在空气中的传播速度。
实验中分别选取测距距离为1和15 m 2个点进行测量, 结果如图 2所示。

|
| 图 2 双向测距算法实测结果 Fig. 2 Measured results of two-way ranging algorithm |
由实验可得, 测距精度在±5 cm, 响应时间5 ms, 满足机器人控制对定位的实时性和准确性要求。但是在实验过程中, 发现会随机出现奇异值。奇异值的出现对后续的机器人定位, 轨迹跟踪等会有极大的影响, 甚至会出现机器人失控等反应, 所以在1.2节设计了奇异值去除模块。
1.2 改进的马氏距离奇异值检测算法针对UWB测距随机出现的奇异值, 本系统对马氏距离奇异值检测算法进行了改进, 设计了奇异值去除模块。传统马氏距离奇异值检测算法直接利用传感器测得数据的均值和协方差矩阵计算马氏距离, 算出来的结果有可能是不稳健的, 容易受到奇异值遮蔽作用的影响, 导致正常数据和奇异值算出来的马氏距离差别不大, 从而无法去除奇异值。而基于最小协方差行列式(Minimum Covariance Determinant, MCD)估计的马氏距离奇异值检测算法中, 所利用的均值和协方差矩阵都是在MCD估计中计算出的稳健估计量, 奇异值和正常数据的马氏距离有较大差值, 从而达到检测并去除奇异值的作用。
有一组数据集合D={xi|i=1, 2, …}, 若T为均值, S为协方差矩阵, 设B=[xi-T](i=1, 2, …), 则该组数据的马氏距离计算公式为
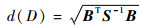
|
(3) |
得到的马氏距离近似服从自由度为p的卡方分布, 在一定置信度下设定阈值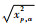
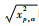
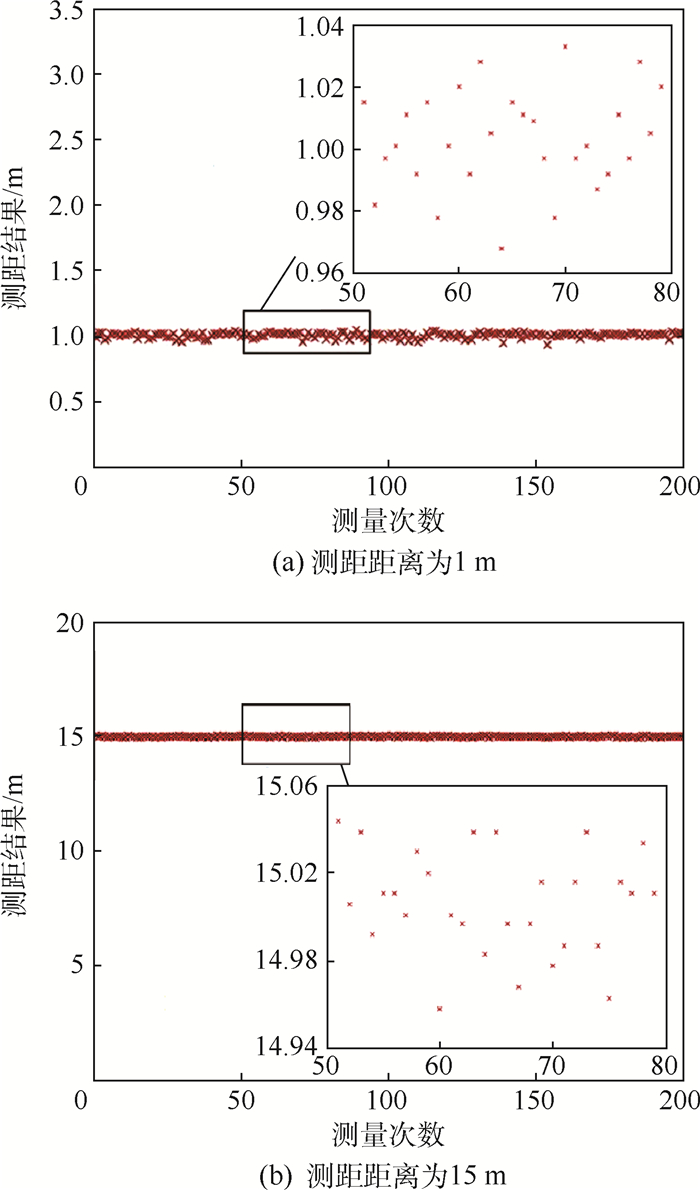
基于MCD的马氏距离奇异值检测算法即采用Rousseeuw和Driessen提出的FAST-MCD算法[18], 首先, 通过迭代得到稳健的均值和协方差矩阵, 然后再计算稳健的马氏距离, 最后进行奇异值检测。算法流程如图 3所示。实验中, 仍选取测距距离为1和15 m 2个点进行测量, 结果如图 4所示。

|
| 图 3 基于MCD的马氏距离奇异值检测算法流程图 Fig. 3 Flowchart of Mahalanobis distance singular value detection algorithm based on MCD |
|
| 图 4 基于稳健马氏距离奇异值去除之后的测距结果 Fig. 4 Ranging results based on robust Mahalanobis distance after removal of singular value |
由实验可得, 测距精度在±5 cm, 响应时间为5 ms, 奇异值被去除。实验证明, 基于MCD的马氏距离奇异值检测算法, 能够在不影响测距实时性的前提下, 有效去除随机出现的奇异值。
1.3 位置测算模块考虑到UWB模块可以得到较为准确的两点之间距离, 加之三边测量法计算量小易于实现, 所以系统运用该算法进行位置测算。
已知锚点坐标为(x1, y1, z1), (x2, y2, z2), (x3, y3, z3), (x4, y4, z4), 未知点坐标为(x0, y0), 以及未知点到4个已知锚点的距离分别为d1, d2, d3, d4, 由此可得
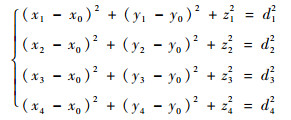
|
(4) |
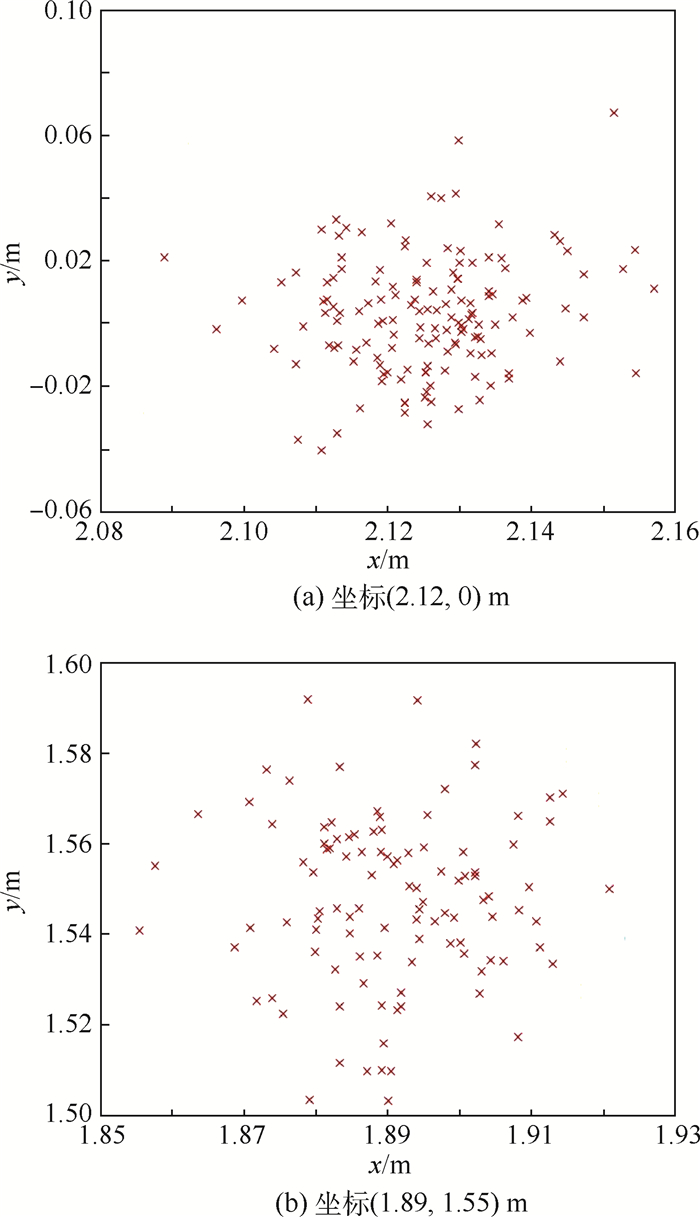
实验中, 实测了2组xy平面坐标, 1组为x轴边界附近点, 1组为一般点, 如图 5所示。
|
| 图 5 三边测量法的实测结果 Fig. 5 Measured results of trilateration algorithm |
由实验可得, 坐标测量较准确, 测量误差±4 cm, 但是在坐标轴边界附近的点, 误差偏大为±8cm, 分析其主要原因是三边测量法在边界处将UWB测距误差的影响放大了。针对一般点误差和边缘效应, 后续依据机器人运动学和动力学模型, 设计了基于扩展卡尔曼滤波(EKF)的优化算法, 对得到的坐标进行优化处理。
2 异构机器人轨迹跟踪控制针对全向机器人的运动学和动力学特点, 提出了一种基于滑模+PID控制的逆动力学前馈控制算法; 针对UWB定位算法中出现的坐标跳动、边缘效应以及微型四旋翼的运动学特点, 设计了基于EKF的轨迹跟踪控制算法。
2.1 全向机器人控制全向机器人为实验室自行设计, 大小20 cm×20 cm, 高12 cm, 续航2 h。
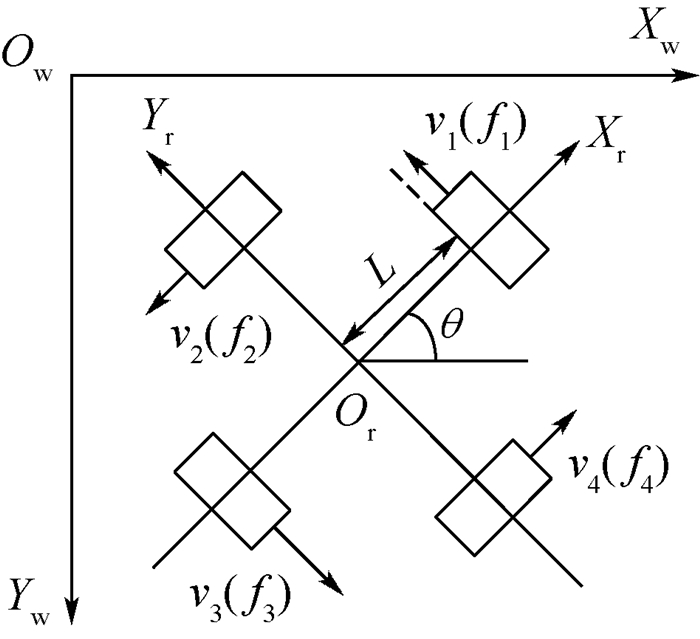
四轮全向机器人的坐标系如图 6所示, 其中Ow-XwYw是以锚点为基点的全局坐标系, Or-XrYr为相对坐标系; (xw, yw, θw)为全局坐标系下机器人位姿, (xr, yr, θr)为相对坐标系下机器人位姿; v1~v4为机器人轮子线速度, θ为方位角, L为轮子到质心的距离, f1~f4为每个全向轮上的驱动力。
|
| 图 6 四轮全向机器人坐标系 Fig. 6 Coordinate system of four-wheeled omnidirectional robot |
分析可得四轮全向机器人的运动学模型为
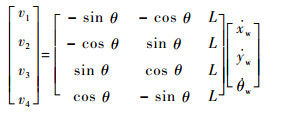
|
(5) |
动力学模型为
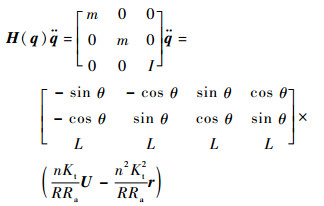
|
(6) |
式中:m为机器人总质量; I为机器人绕中心旋转的转动惯量; R为轮子半径; Ra为电机的电枢电阻; Kt为电机转矩常数; U=(U1, U2, U3, U4)T为电机电压; r=(r1, r2, r3, r4)为轮子转速; q为全局坐标系下机器人坐标; n为电机齿轮减速比。
假设期望轨迹为qd(t)=(xd(t), yd(t), θd(t))T, 期望速度为vd=(vxd, vyd, wd)T。
运动学控制设计如下:
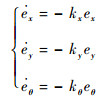
|
(7) |
式中:eq=(ex, ey, eθ)为轨迹跟踪误差; kx, ky, kθ>0为运动学参数。
由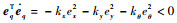
设ωi为全向轮的角速度, 则vi=Rωi, 由式(5)可得

|
(8) |
将式(8)代入式(6)可得

|
(9) |
式中:
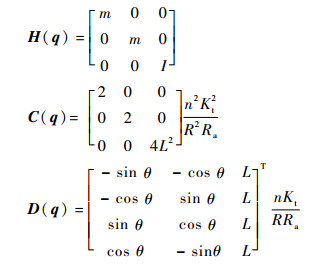
|
实际应用中, 因为存在扰动, 所以式(9)通常为
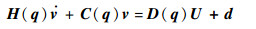
|
(10) |
式中: 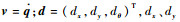
设控制律为
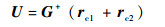
|
(11) |
式中:G=H0-1D(q), H0=a0H(q), 0 < a0 < 1;G+为G的广义逆矩阵, G+=GT(GGT)-1; rc1为PID控制信号; rc2为动力学前馈的控制信号。设
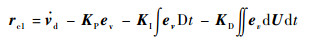
|
(12) |
式中:KP、KI、KD分别为PID控制中3个分量上的系数; ev=v-vd。由式(11)可得
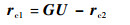
|
(13) |
由式(10)可得
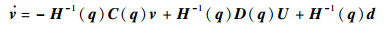
|
(14) |
由式(13)和式(14)可得
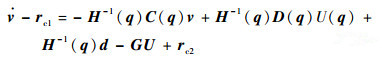
|
(15) |
由式(12)可得
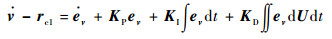
|
(16) |
式(15)和式(16)联立可得
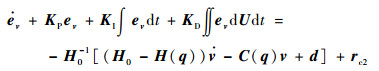
|
(17) |
将式(17)按状态方程写为
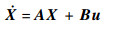
|
(18) |
式中:
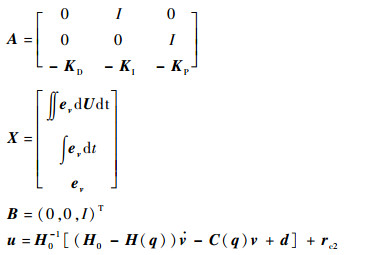
|
选定滑模面为
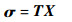
|
(19) |
式中:

|
由滑模控制原理可知, 当X移动到滑模面σ=0时, 
令
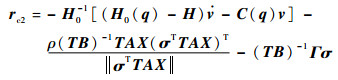
|
(20) |
式中:Γ=ΓT>0为待设计控制系数。

|
ρ参数可以确保误差状态方程在一定时间内趋近于0。假设有拉格朗日方程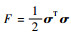
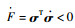
为适应机器人越来越小型化的趋势, 微型四旋翼选择开源飞机crazyflie2.0, 该飞机大小只有9 cm×9 cm, 质量27 g, 续航7 min。研究中针对飞机尺寸设计了适应飞机载重和尺寸的UWB模块(大小3 cm×2 cm, 质量6 g), 编写了位置控制环和坐标系变换函数, 基于UWB的运动学模型和测量模型分析如下。
若UWB在飞机运行中某一节点测得位置为S=(Sx, Sy, Sz)T, 估计的速度为v=(vx, vy, vz)T, 假设加速度a=(ax, ay, az)T在时间[tk-1, tk]保持不变, 则可得到该节点的离散模型为
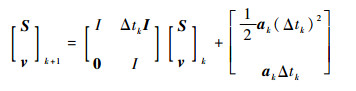
|
(21) |
式中:Δtk为相邻时间差, 下标k表示时间序列; ak为tk时刻加速度。
离散模型基于UWB的测量方程为
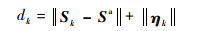
|
(22) |
式中:dk为UWB测得的标签到各个锚点的距离; Sa=(xa, ya, za)为锚点的位置; ηk为测量误差。
综上所述, 基于UWB的crazyflie2.0的运动学和测量模型可以写为

|
(23) |
式中:εk为[tk, tk+1]时间内的运动增量; 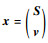
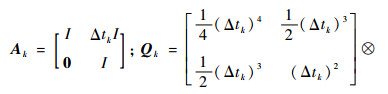
|
diag(σx2, σy2, σz2); Rv为方差。
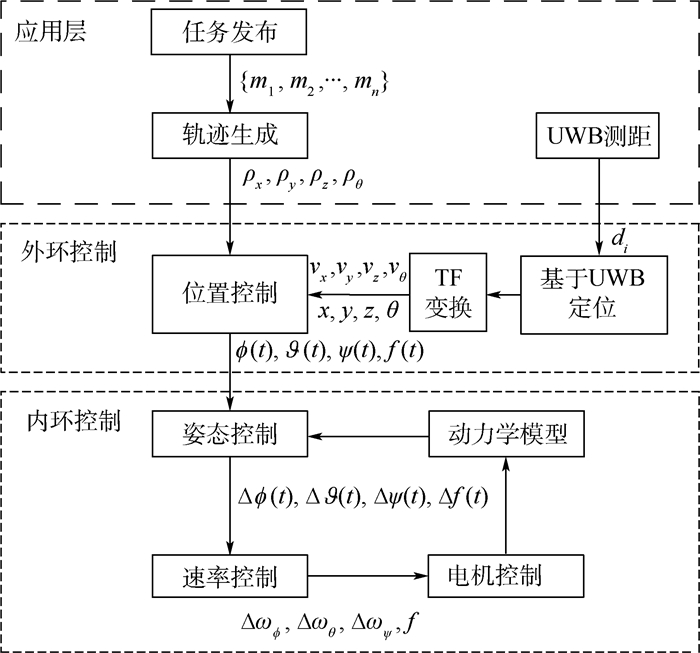
基于UWB的crazyflie2.0自主控制流程图如图 7所示。其中, {m1, m2, …, mn}为任务列表, ρx、ρy、ρz和ρθ为依据任务生成的期望轨迹, di为UWB测距结果, vx、vy、vz和vθ为当前四旋翼飞行速度, x、y、z和θ为四旋翼在全局坐标系下的位姿信息, φ(t)、∂(t)、ψ(t)和f(t)为经过位置控制环解析出的与期望轨迹的差值, Δφ(t)、Δ∂(t)、Δψ(t)和Δf(t)为经过姿态控制环解析的与期望姿态的差值, Δωφ、Δωθ、Δωψ和f为经过速率控制环解析的期望控制量。
|
| 图 7 基于UWB的crazyflie2.0自主控制流程图 Fig. 7 Flowchart of crazyflie2.0 autonomous control based on UWB |
针对坐标跳动偏大问题, 基于crazyflie2.0的运动学模型, 采用EKF算法设计了优化模块。算法原理如下:
输入:t-1时刻状态(x, y)t-1, St-1; t时刻控制信号ut; t时刻观测值zt。
输出:t时刻状态(x, y)t, St。
1 predict(((x, y)t-1, St-1, ut))→((x, y)t-, St-)
2 update((x, y)t-, St-, zt)→((x, y)t, St)
3 return(x, y)t, St
其中:函数predict()和update()是卡尔曼滤波的标准程序, 以2.2.1节分析的crazyflie2.0运动学和测量模型为例, 则此时predict()为
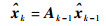
|
(24) |

|
(25) |
式中:“^”表示估计值, “-”表示先验值。
update()为
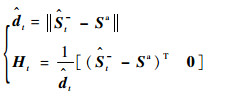
|
(26) |

|
(27) |
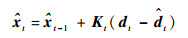
|
(28) |
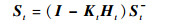
|
(29) |
式中:Sa为锚点位置。
3 实验 3.1 算法仿真实验 3.1.1 全向机器人轨迹跟踪算法在MATLAB中对全向机器人控制算法进行了仿真验证。仿真中设定L=0.12 m, m=2 kg, I=1.013 kg·m2, Kt=0.014, R=0.03 m, Ra=1.9 Ω。设期望轨迹函数为
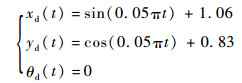
|
(30) |
设定参数kx=ky=kθ=0.8, H0=0.7H, ρ=40, 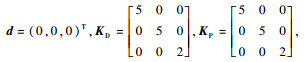


|
| 图 8 轨迹跟踪仿真实验结果 Fig. 8 Trajectory tracking simulation experimental results |

|
| 图 9 轨迹跟踪误差随时间变化 Fig. 9 Variation of trajectory tracking deviation with time |
实验结果表明, 全向机器人轨迹跟踪状态良好, 响应速度快, 稳态误差为0, 验证了轨迹跟踪控制算法的有效性, 可以将该算法用于实际全向机器人的轨迹跟踪控制。
3.1.2 基于EKF优化的crazyflie2.0轨迹跟踪算法利用ROS在Gazebo中对crazyflie2.0改进后的轨迹跟踪算法进行了仿真, 验证了EKF优化模块的有效性。实验中, 实地采集了一组UWB数据作为飞机的飞行轨迹的实测值, 仿真结果如图 10所示。

|
| 图 10 基于EKF crazyflie2.0运行轨迹 Fig. 10 crazyflie2.0 running trajectory based on EKF |
实验结果表明, 通过EKF优化模块对数据进行处理后, 飞行轨迹与期望轨迹基本重合, 有效抑制了坐标跳动对飞行控制的影响, 可以将该算法用于实际crazyflie2.0的轨迹跟踪控制。
3.2 异构多机器人平台算法验证基于UWB在ROS框架下构建了多机器人研究平台, 系统共包含4个全向机器人和一个crazyflie2.0微型四旋翼, 实验平台如图 11所示。基于整套系统, 分别完成了单全向机器人轨迹跟踪实验、crazyflie2.0的定点悬停实验和多机器人协同控制实验, 验证了UWB定位和机器人控制算法的实时性、稳定性和准确性。

|
| 图 11 多机器人研究平台 Fig. 11 Multi-robot research platform |
设计中每个全向机器人搭载微处理器树莓派并安装Ubuntu系统及ROS操作平台, 中央处理机直接控制crazyflie2.0并对所有机器人进行监控。中央处理机分配任务后, 每个全向机器人依据自己得到的任务信息, 规划路径, 完成轨迹跟踪并向云端发送消息, 通告所有机器人其目前状态。crazyflie2.0由中央处理机完成路径规划并通过数传发送给飞机实现控制。
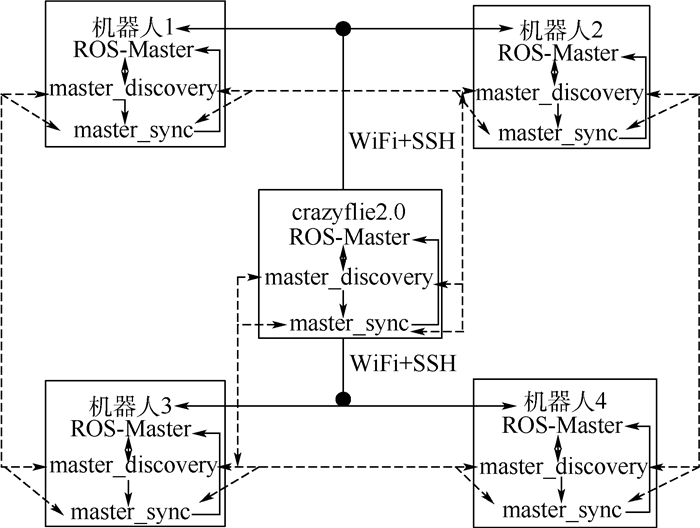
系统通过WiFi进行通信, 中央处理机通过SSH工具远程登录各个机器人, 从而实现离板控制。在中央处理机和每个机器人上运行roscore, 即每个机器人包括中央处理机都作为一个独立的master, 这样设计有2个优点:第一, 假如某一个机器人出现问题或是中央处理机出现故障, 不会造成整个多机器人系统瘫痪或运行混乱; 第二, 方便设计加入与退出机制, 在运行过程中添加或减少机器人个数, 例如某一机器人完成所分配任务后, 可以选择退出多机器人系统, 这样有助于减少中央处理机的负担。在这里构建的多机器人系统, 通过github中master_discovery和master_sync2个开源项目, 对机器人加上时间标签, 并进行时间同步。多机器人系统网络示意图如图 12所示。
|
| 图 12 多机器人系统网络示意图 Fig. 12 Schematic diagram of multi-robot system network |
由于UWB在不同环境使用时会受到经纬度、海拔高度、空气质量、障碍物等影响, 因此在实验前需要进行标定。
在室内[0.4, 4] m实测了已知真实距离的50组数据, 然后进行曲线拟合, 考虑到需要满足精度要求前提下, 又不影响计算速度, 因此采取3次多项式拟合, 得到拟合函数为
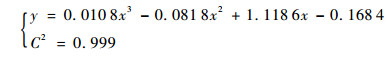
|
式中:C为相关系数, C2越趋近于1拟合曲线越精确。
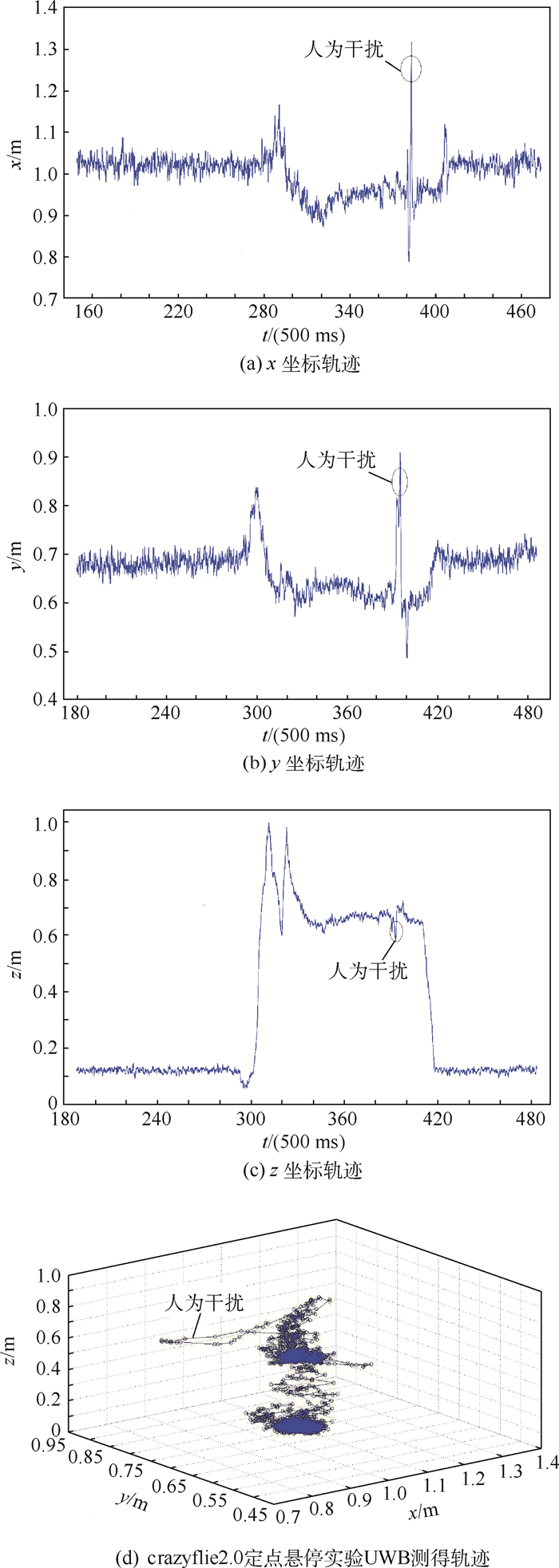
3.2.3 crazyflie2.0定点悬停实验为了验证crayflie2.0轨迹跟踪控制算法和快速运动中UWB定位的实时性、准确性, 设计了crazyflie2.0定点悬停实验。实验中, 首先读取当前位置(x, y, z), 设定目标点为(x, y, z+0.5)。当飞机悬停后, 用较大力气推动飞机施加干扰, 验证位置控制环的鲁棒性和抗干扰性。实验中UWB实测结果如图 13所示。
|
| 图 13 crazyflie2.0定点悬停UWB实测结果 Fig. 13 Measured UWB results of crazyflie2.0 fixed point hovering |
由实验可得:①实验中, 位置跟踪状态良好, 在悬停位置时x与y方向UWB定位精度在±8 cm, z方向的定位精度在±6 cm, 位置刷新率为30 Hz。在人为施加干扰后, 飞机能立即做出机动, 在4 s内再次回到目标位置, 并进入稳定状态。②2016年bitcraze研究组[12]发布在YouTube的实验, 使用6个锚点做了基于UWB的crazyflie2.0定点悬停实验, 但在实验中, 未对UWB数据进行处理, 仅做了基本应用。本实验只用了4个锚点, 同时对测得的数据进行奇异值去除处理, 并设计了EKF优化模块, 飞行控制更加稳定、响应更加迅速, 实验结果已经发布在YouKu上, 但在实际实验中, 起飞阶段过调达到30 cm, 且人为干扰后, “对抗”机动响应不够强烈, 后续研究可针对这两方面对控制算法进行改进。
3.2.4 单全向机器人轨迹跟踪实验为了验证全向机器人控制算法和UWB定位精度, 设计了单机器人轨迹跟踪实验。设定机器人期望轨迹函数为

|
(31) |
需要注意的是, 目前, 由于全向机器人未搭载其他任何传感器, 只依靠UWB定位系统进行控制, 所以当机器人初次开机时, 需要进行初始姿态判断。设计中, 机器人开机后先向机体坐标系的x轴方向移动20 cm, 然后再退回原位, 从而判断出机器人的初始姿态。实验结果如图 14所示。

|
| 图 14 单机器人sin x轨迹跟踪 Fig. 14 Single robot sin x trajectory tracking |
由实验可得, 机器人轨迹跟踪状态良好, 误差在4 cm, 验证了算法的实时性和鲁棒性, 同时可见, 在弯道处UWB测量点较多, 是由于目前控制算法为了得到平滑的运行轨迹, 在遇到大角度弯道时会降速行驶, 后续可进行大角度弯道快速通过的控制算法研究。
3.2.5 多机器人协同控制实验为了验证机器人控制算法、多机器人系统和通信网络鲁棒性、异构机器人协作及多机器人条件下UWB的定位精度, 设计了简单的异构多机器人协同控制实验。
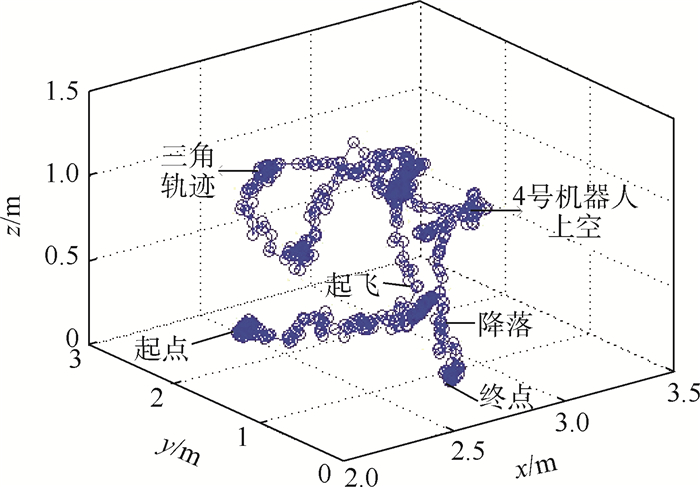
实验内容:①全向机器人1号、2号、3号、4号分别移动到点(1.0, 0.8) m, (1.0, 1.8) m, (3, 1.8) m, (3, 0.8) m, crazyflie2.0置于3号全向机器人上, 设定互不碰撞优先级为1号>2号>3号>4号, 当任意两车x或y坐标相差小于10 cm时优先级低的停车等待; ②各全向机器人到达目标点后, 3号机器人等待crazyflie2.0起飞, 1号、2号、4号机器人开始跟踪椭圆轨迹; ③crazyflie2.0起飞, 3号机器人跟踪椭圆轨迹; ④crazyflie2.0到达悬停点后, 跟踪三角形轨迹一周; ⑤4号车停车等待, crazyflie2.0自主跟踪4号车, 先移动到4号车正上方后再垂直降落。实验结果如图 15和图 16所示。
|
| 图 15 crazyflie2.0协同任务实验轨迹 Fig. 15 Experimental trajectory of crazyflie2.0 collaborative task |
|
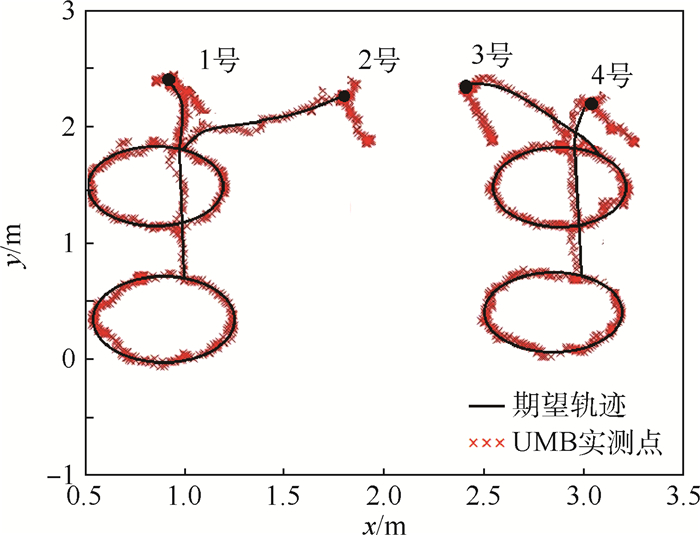
| 图 16 全向机器人协同任务实验轨迹 Fig. 16 Experimental trajectory of omnidirectional robot collaborative task |
由实验可得, 多机器人网络通信实时流畅, 在实际多机器人条件下, 异构移动机器人的轨迹跟踪误差在6 cm, 能够在室内实现有效、稳定、实时的轨迹跟踪, 验证了控制算法的实时性和稳定性。但目前只是进行了简单的异构机器人协同实验, 后续可基于该平台继续研究:①微型四旋翼降落到移动中的全向机器人上; ②空地多机器人编队控制算法研究。
4 结论本文基于UWB以全向机器人和crazyflie2.0四旋翼为基础, 提出了基于滑模+PID控制的逆动力学前馈控制算法和基于EKF优化的轨迹跟踪控制算法, 并进行了仿真验证。
1) 搭建了异构多机器人研究平台, 基本解决了传统多机器人控制算法到实践之间脱节的问题, 相较于基于运动捕获系统的研究平台, 性价比显著提高, 应用范围更加广泛, 且该平台传输数据非常简单, 对机器人数据处理能力要求低, 有利于真正实现移动机器人的自主控制。
2) 实验结果表明UWB定位与轨迹跟踪控制算法的实时性和准确性能够满足机器人控制要求。另外,多机器人协同控制实验为后续多机器人编队、轨迹跟踪控制算法研究奠定基础。
| [1] | SUEOKA S, IRIE T. The study for control of the robot plane with GPS and IMU[J]. Journal of Medical Virology, 2016, 13 : 417–418. |
| [2] | SASANI S, ASGARI J, AMIRI-SIMKOOEI A R. Improving MEMS-IMU/GPS integrated systems for land vehicle navigation applications[J]. GPS Solutions, 2016, 20 (1): 89–100. DOI:10.1007/s10291-015-0471-3 |
| [3] | LI J, SONG N, YANG G, et al. Improving positioning accuracy of vehicular navigation system during GPS outages utilizing ensemble learning algorithm[J]. Information Fusion, 2017, 35 (C): 1–10. |
| [4] | SAEEDI S, TRENTINI M, SETO M, et al. Multiple-robot simultaneous localization and mapping:A review[J]. Journal of Field Robotics, 2016, 33 (1): 3–46. DOI:10.1002/rob.21620 |
| [5] | LOPEZ E, GARCIA S, BAREA R, et al. A multi-sensorial simultaneous localization and mapping (SLAM) system for low-cost micro aerial vehicles in GPS-denied environments[J]. Sensors, 2017, 17 (4): 802. DOI:10.3390/s17040802 |
| [6] | AGHILI F, SU C Y. Robust relative navigation by integration of ICP and adaptive Kalman filter using laser scanner and IMU[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21 (4): 2015–2026. DOI:10.1109/TMECH.2016.2547905 |
| [7] | STACHNISS C, KRETZSCHMAR H. Pose graph compression for laser-based SLAM[M]//CHRISTENSEN H, KHATIB O. Robotics research. Berlin: Springer, 2017: 271-287. |
| [8] | ENDRES F, HESS J, STURM J, et al. 3-D mapping with an RGB-D camera[J]. IEEE Transactions on Robotics, 2017, 30 (1): 177–187. |
| [9] | GAO X, ZHANG T. Unsupervised learning to detect loops using deep neural networks for visual SLAM system[J]. Autonomous Robots, 2017, 41 (1): 1–18. DOI:10.1007/s10514-015-9516-2 |
| [10] | CAO J, ZENG B, LIU J, et al. A novel relocation method for simultaneous localization and mapping based on deep learning algorithm[J]. Computers & Electrical Engineering, 2017, 63 (10): 79–90. |
| [11] | ERYILDITIM A, GULDOGAN M B. A Bernoulli filter for extended target tracking using random matrices in an UWB sensor network[J]. IEEE Sensors Journal, 2016, 16 (11): 4362–4373. DOI:10.1109/JSEN.2016.2544807 |
| [12] | crazyflie2. 0[EB/OL]. [2017-04-20]. https://www.bitcraze.io. |
| [13] |
张一淳, 张雪波, 方勇纯, 等. 基于主动偏心轮的全方位移动机器人航位推算与跟踪控制[J].
机器人, 2015, 37 (3): 361–368.
ZHANG Y C, ZHANG X B, FANG Y C, et al. Dead reckoning and tracking control of omnidirectional mobile robots[J]. Robot, 2015, 37 (3): 361–368. (in Chinese) |
| [14] | MADHUSUDHAN M G. Control of crazyflie nano quadcopter using Simulink[M]. Long Beach: California State University, 2016. |
| [15] | JAFAROV S M, ZEYNALOV E R, MUSTAFAYEVA A M. Synthesis of robust controller-regulators for omnidirectional mobile robot with irregular movement[J]. Procedia Computer Science, 2016, 102 : 469–476. DOI:10.1016/j.procs.2016.09.429 |
| [16] | HAMMER F, YUDANTO R, KAI N, et al. Performance evaluation of 3D-position estimation systems[J]. IEEE Sensors Journal, 2016, 16 (16): 6416–6424. DOI:10.1109/JSEN.2016.2581489 |
| [17] |
阴盼强, 路东明, 袁渊, 等. 基于马氏距离的改进非局部均值图像去噪算法[J].
计算机辅助设计与图形学学报, 2016, 28 (3): 404–410.
YIN P Q, LU D M, YUAN Y, et al. An improved non-local means image de-noising algorithm using Mahalanobis distance[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28 (3): 404–410. (in Chinese) |
| [18] | ROUSSEEUW P J, DRIESSEN K V. A fast algorithm for the minimum covariance determinant estimator[J]. Technometrics, 1999, 41 (3): 212–223. DOI:10.1080/00401706.1999.10485670 |



