2. 中国民航大学 工程技术训练中心, 天津 300300
2. Engineering Technology Training Center, Civil Aviation University of China, Tianjin 300300, China
民航发动机广泛使用可调静子叶片(VSV)系统来提高发动机工作稳定性,防止发动机失速或喘振等不稳定工作状态的产生。VSV系统的主要作用是通过调整VSV的角度,使气流以最佳攻角进入压气机转子叶片,避免出现涡流和气流阻塞,减少气流损失[1],达到提高发动机工作稳定性的目的。发动机VSV系统结构复杂、调节频繁,容易发生故障,严重时会引起发动机喘振[2]。因此,对发动机VSV的调节规律进行研究对于发动机故障诊断和安全高效的运营至关重要。在VSV调节角度设计及对发动机性能影响方面,黄爱华[3]通过发动机试车数据研究了发动机在高低转速下的VSV调节规律,分析了叶片角度调节对发动机性能的影响;吴秀宽和林森[4]通过基准气流角法估算了风扇可调导流叶片的调节规律,并通过特性分析法进行了验证;曹志鹏等[5]将特性计算程序与导、静叶角度优化调节方案相结合,确定了不同转速下导、静叶的最佳调节角度;张健和任铭林[6]通过试验确定了压气机VSV在设计转速下的最佳组合角度。
目前,中国民航使用的发动机均为国外厂家制造,VSV控制规律属技术保密,同时也罕见对其状态监控和故障诊断方面的研究。近年来,基于大数据,支持向量机、神经网络等智能算法开始应用于发动机故障诊断[7-9]、数据回归与性能预测[10-11]。本文以蕴含发动机工作状态信息的快速存取记录装置(QAR)数据为基础,基于粒子群优化(PSO)算法和支持向量回归机(SVR)建立PW4077D发动机的VSV调节规律模型,以探索VSV调节规律,对于VSV的位置监控和故障诊断具有重要的意义。
1 算法理论 1.1 支持向量回归机支持向量机是一种基于统计学习理论的机器学习方法,通过寻求结构风险最小来提高学习机泛化能力,其克服了神经网络训练样本需求多、容易陷入局部最优等缺点。
设存在样本集合{(xi, yi), …, (xs, ys)},i=1, 2, …, s。通过求解函数f(x)来预测x对应的y值。
线性函数设为

|
(1) |
式中:ω为权值变量; b为线性函数系数。
引入松弛因子ξi、ξi*和惩罚参数C,优化问题表示为

|

|
(2) |
式中:ε为不敏感损失函数。
为便于求解,将上述二次规划优化问题式(2)转换为其对偶问题:
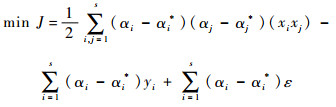
|
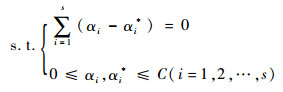
|
(3) |
式中:αi、αi*为拉格朗日系数。
近似的回归模型可表示为

|
(4) |
式中:K(xi, x)为核函数,本文选用的是应用广泛的高斯核,表达式如下:
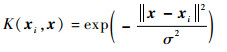
|
(5) |
其中:σ为高斯核宽度系数。
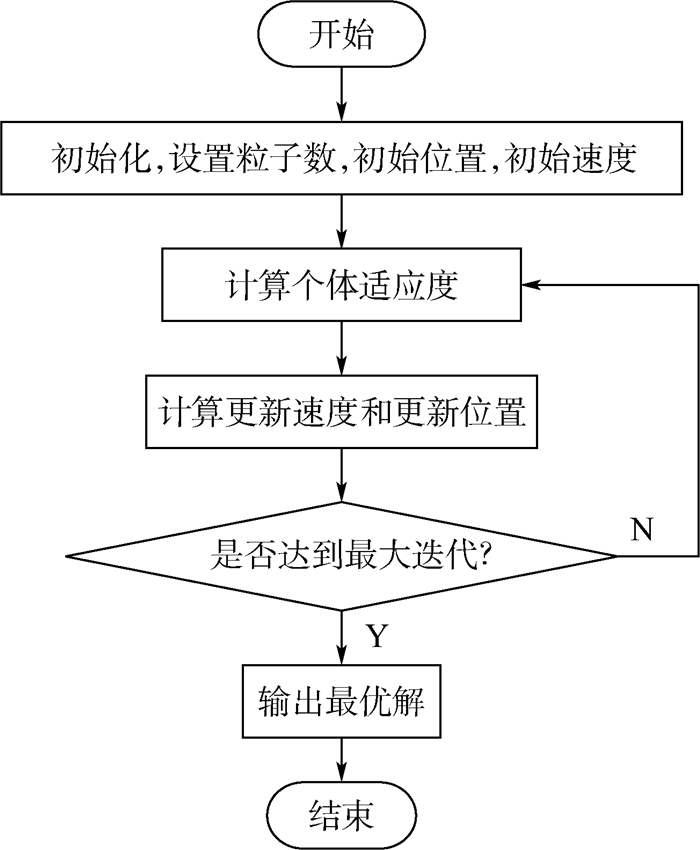
1.2 粒子群优化算法为了保证SVR模型的准确性,需要对惩罚参数C和高斯核参数σ的取值进行优化。PSO算法是一种基于群体智能的优化算法,从一组随机解开始,利用适应度来评价解的品质,通过层层迭代找到最优解[12]。该算法实现容易、精度高、收敛快,并在解决工程实际问题中展示了其优越性。
|
| 图 1 PSO算法流程图 Fig. 1 Flowchart of PSO algorithm |
飞机在下降阶段,环境参数变化大,飞行状况复杂,VSV调节规律复杂,且极易发生故障,因此重点研究此阶段的调节规律。选取某航空公司B777-200飞机的10个正常航班下降段数据作为训练样本,另外4个航班下降段数据作为验证样本。其中代表VSV开度的作动筒位置SVA作为因变量,对于自变量的选取遵循2个原则[14]:①不能漏掉重要的解释因素造成模型失真;②尽量减少自变量个数,降低问题的复杂度。对QAR数据中部分参数与SVA做了相关性分析,筛选出相关性较高的参数,如表 1所示。
| 参数 | 相关系数 |
| N1 CMD | 0.986 |
| N1 | 0.986 |
| Tt3 | 0.973 |
| N2 | 0.939 |
| Ma | 0.901 |
| Tt25 | 0.895 |
| ALTC | 0.871 |
| ALT | 0.871 |
| TRA | 0.820 |
| BP | 0.778 |
| WF | 0.702 |
| TAT | -0.750 |
| Pt5 | -0.767 |
| Tt2 | -0.809 |
| SAT | -0.851 |
| Pt2 | -0.864 |
由表 1可知,多个参数与SVA相关性较大,如指令低压转子转速N1 CMD、低压转子转速N1、高压压气机出口总温Tt3、高压转子转速N2、飞行马赫数Ma、低压压气机出口总温Tt25、粗略飞行高度ALTC、飞行高度ALT、油门杆角度TRA、高压压气机出口总压BP、燃油流量WF、大气总温TAT、低压涡轮出口总压Pt5、低压压气机进口总温Tt2、大气静压SAT、低压压气机进口总压Pt2。其中低压转子转速N1与SVA的相关系数最高,达到0.986,而高压转子转速N2与SVA的相关系数也达到了0.939。由航空公司维修手册[15]知,PW4077D发动机的EEC依据N1、N2、低压压气机进口总温Tt2,通过力矩马达控制液压油操作VSV作动筒,改变VSV位置,所以自变量中应有N1、N2、Tt2。
低压压气机进口总压、飞行马赫数和飞行高度有固定的函数关系,考虑到飞行高度与大气湿度相关,飞行马赫数反映了飞行的速度特性,为避免信息重复,这3个参数仅保留飞行高度和马赫数作为变量。同时为保证模型的准确性和可行性,保留表 1中与SVA相关系数较高且影响燃油流量的油门杆角度TRA、反映VSV前后总温变化的Tt25和Tt3。
综上所述,建立模型的变量确定为低压转子转速N1、高压转子转速N2、低压压气机进口总温Tt2、飞行高度ALT、飞行马赫数Ma、油门杆角度TRA、低压压气机出口总温Tt25和高压压气机出口总温Tt3。
2.1.2 数据预处理由于不同的航班所经历的外界大气条件不同,主要的性能参数差别很大,所以需要对样本数据进行相似处理。
根据相似理论[16],N1、N2的相似修正公式为
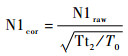
|
(6) |
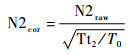
|
(7) |
式中:下标raw表示原始实际转速;下标cor表示修正后的转速;T0为标准大气状态下的温度。
飞机在飞行过程中推力不同,发动机性能参数也不同。因此要对上述数据功率修正,根据普惠公司的ECM手册[17],修正公式为
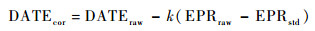
|
(8) |
式中:DATEraw为修正前数据;DATEcor为修正后数据;EPRraw为实际推力值;EPRstd为设定的标准推力值;k为该参数与EPR的斜率关系[18]。
为了避免具有不同量纲的输入变量之间的数量级差别对模型的影响,数据需要进行归一化处理:
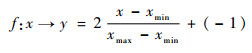
|
(9) |
不同航班的数据经过相似修正、功率修正和归一化处理后,完成数据准备工作。
2.2 支持向量回归机参数优化研究SVR模型的训练相关系数R2和测试相关系数R2随惩罚参数C和核参数σ的变化规律,结果如图 2、图 3所示。
|
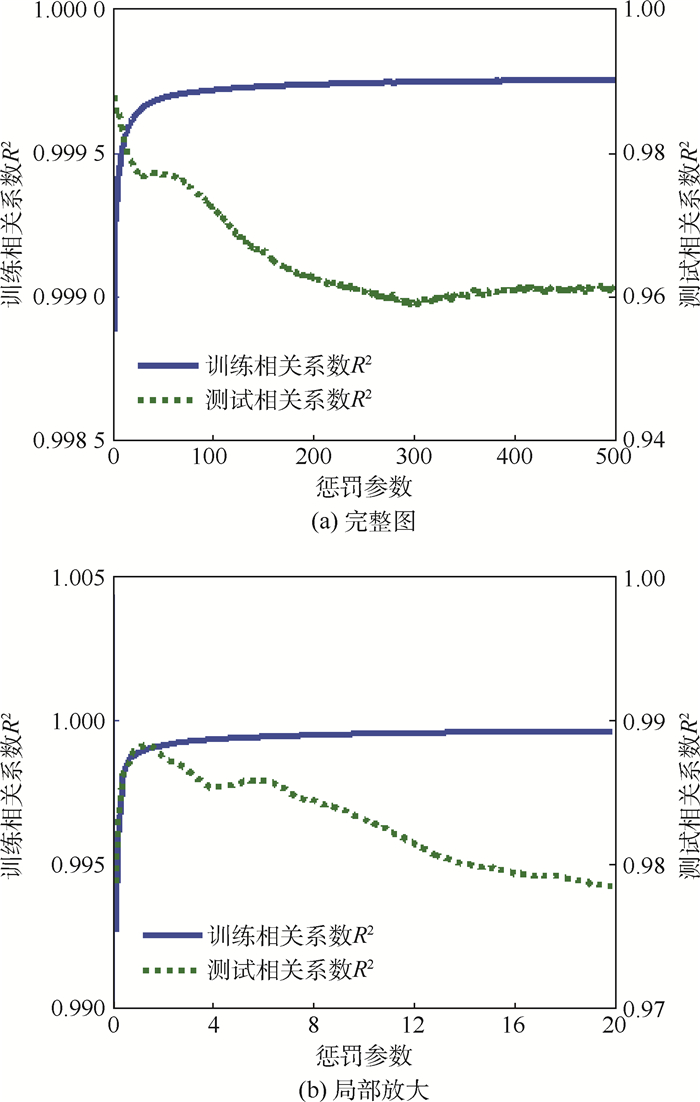
| 图 2 SVR模型训练相关系数和测试相关系数随惩罚参数的变化(σ=5) Fig. 2 Variation of SVR model training correlation coefficient and test correlation coefficient with penalty parameter(σ=5) |
|
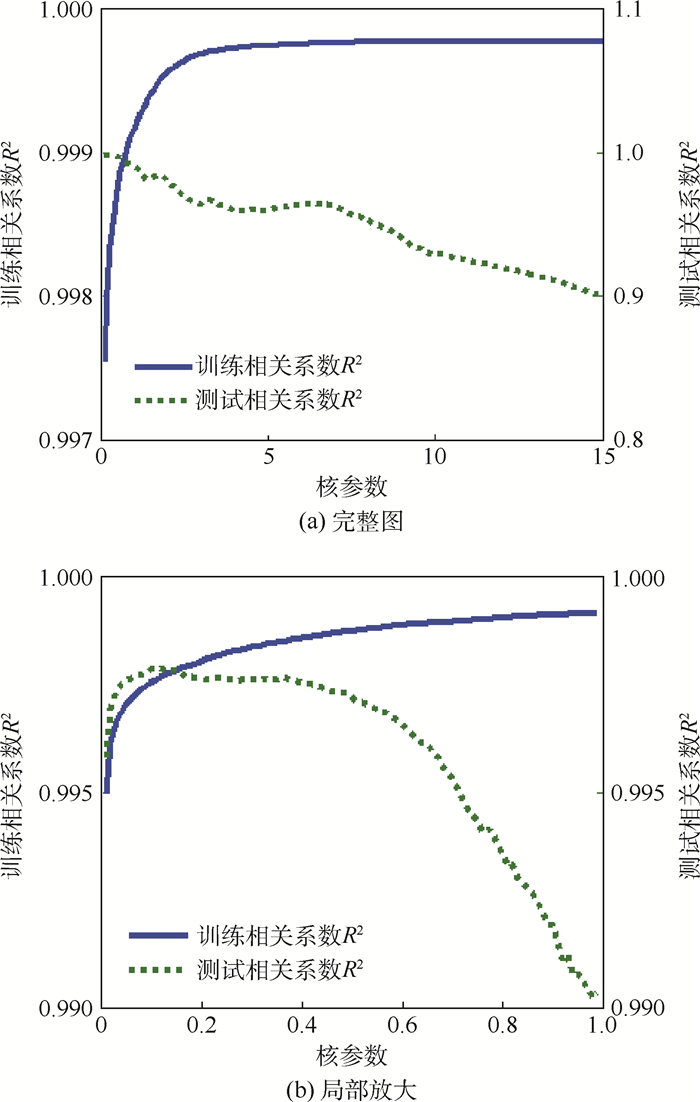
| 图 3 SVR模型训练相关系数和测试相关系数随核参数的变化(C=300) Fig. 3 Variation of SVR model training correlation coefficient and test correlation coefficient with kernel function parameter(C=300) |
由图 2可知,在核参数一定时,训练相关系数随着惩罚参数的增大首先急剧增大,最后趋于平稳;而测试相关系数首先在一个很小的范围内增大然后减小最后趋于平稳,模型的学习推广能力经历了由低到高再到低的过程,说明惩罚参数过大或过小都会导致模型泛化能力降低。另外训练相关系数和测试相关系数的最大值并不重合,说明传统的经验风险最小化并不能保证良好的推广能力。
由图 3可知,在惩罚参数一定时,随着核参数的增大,训练相关系数急剧增大而后趋于平稳,测试相关系数首先增大而后减小,说明核参数取值不当会使模型学习推广能力降低。
综上分析,惩罚参数C与高斯核参数σ的选取对回归效果有显著影响。为了得到精度较高的模型,利用PSO算法对2个参数进行了优化。
通过调用LIBSVM工具箱中相关函数,初始化各参数,迭代200次得到粒子群优化结果为:Cbest=100, σbest=0.503 12,进化代数曲线如图 4所示,模型经过120次迭代后趋于收敛,最佳适应度趋于稳定。

|
| 图 4 PSO算法进化曲线 Fig. 4 Evolution curves of PSO algorithm |
下面建立基于PSO-SVR的VSV调节规律模型,依据2.1.1节分析,输入量设置为8个影响参数:ALT、Ma、TRA、N1、N2、Tt2、Tt25、Tt3,输出量设置为SVA。PSO-SVR模型训练的相对误差率如图 5所示。

|
| 图 5 PSO-SVR模型训练的相对误差率 Fig. 5 Relative error rate of PSO-SVR model training |
由图 5可知,由PSO-SVR建立的VSV调节规律模型的训练相对误差率较小,大部分在-5%~5%之间。考虑到下降阶段发动机性能状态变化较大,飞行员操纵频繁等原因使VSV角度调节幅度和频率都大于其他阶段,该误差是可以接受的。
为了验证所建立的PSO-SVR模型的学习推广能力,另选取B777-200飞机4个航班的QAR数据进行验证,同时将验证结果与传统的PSO-BP神经网络模型进行对比,来检测PSO-SVR模型在VSV调节规律预测方面的优劣性。评价指标选择均方误差MSE和相关系数R2,4个航班的预测结果如表 2所示。
| 验证航班 | PSO-SVR模型 | PSO-BP神经网络模型 | |||
| MSE | R2/% | MSE | R2/% | ||
| a | 8.20×10-4 | 99.57 | 1.05 | 97.60 | |
| b | 6.08×10-4 | 99.76 | 0.65 | 99.03 | |
| c | 1.00×10-3 | 99.67 | 1.34 | 98.69 | |
| d | 7.80×10-3 | 99.69 | 0.97 | 99.08 | |
从表 2可以看出:①PSO-SVR模型的均方误差MSE都接近0,相关系数R2都接近1,说明PSO-SVR模型的预测值与实际数据的相关度高、误差小,模型的预测精度高;②PSO-SVR模型的均方误差均小于PSO-BP神经网络模型,相关系数均大于PSO-BP神经网络模型,说明PSO-SVR模型的预测精度、学习泛化能力均优于PSO-BP神经网络模型。另外,通过SVR建立模型训练样本学习时间更少、收敛速度更快。综合来看,PSO-SVR模型优于PSO-BP神经网络模型,在一定范围内能够准确反映飞机下降阶段VSV调节规律,可以为发动机故障诊断提供参考。
3 基于PSO-SVR模型的故障诊断通过健康状态QAR数据建立的PSO-SVR模型可作为基准,如果实际运行中VSV调节开度偏离过大,则可判断为VSV系统故障。利用PSO-SVR模型对2个航班的下降阶段进行监控,如图 6所示。

|
| 图 6 2个航班的监控结果 Fig. 6 Monitoring results for two flights |
由图 6(a)航班e监控结果可知,VSV角度的实际值与回归预测值相差不大,相对误差率大多集中在-5%~5%之间,在下降后期波动较大,但仍处于可以接受的范围之内。说明该航班VSV调节开度正常。
对于航班f(见图 6(b)),PSO-SVR模型回归数据与实际数据前期吻合较好,从275点开始出现较大误差,最大相对误差率达到-60%,明显大于正常航班的相对误差率,判断该航班的VSV系统发生故障。经航空公司实际排故检测发现,该航班是VSV作动筒故障,使VSV卡滞,导致发动机从275点开始发生喘振,并于526点发生了空中停车。
基于PSO-SVR建立的VSV调节规律模型可用于VSV系统故障的初步诊断,再结合孔探或其他技术手段对VSV系统的各个部件(如作动筒、曲柄机构、同步作动环、作动杆等)进一步检查,可最终实现故障隔离。
4 结论1) 支持向量回归机惩罚参数和高斯核参数对回归模型的预测精度有较大影响,过大或过小都会降低模型的学习推广能力,本文应用PSO算法实现了对两者的优化。
2) PSO-SVR模型的回归预测精度优于传统的PSO-BP神经网络模型,具有更好的泛化性能,在一定范围内能够准确反映VSV调节规律。
3) PSO-SVR模型能够实现VSV位置监控和VSV系统故障的初步诊断,为发动机状态监控和故障诊断提供帮助。
| [1] |
唐庆如, 孔萌. CFM56-7B发动机VSV结构损伤分析[J].
航空维修与工程, 2011 (4): 31–33.
TANG Q R, KONG M. Analysis of CFM56-7B VSV structural damage[J]. Aviation Maintenance Engineering, 2011 (4): 31–33. (in Chinese) |
| [2] |
李世林. VSV系统对CFM56发动机喘振的影响分析[J].
科学技术与工程, 2011, 11 (20): 4934–4936.
LI S L. Research on VSV faults based CFM56 engine surge[J]. Science Technology and Engineering, 2011, 11 (20): 4934–4936. DOI:10.3969/j.issn.1671-1815.2011.20.063 (in Chinese) |
| [3] |
黄爱华. 涡扇发动机可调静子叶片控制规律研究[J].
燃气涡轮试验与研究, 2017, 30 (1): 48–51.
HUANG A H. Control law of variable stator vane for turbofan engine[J]. Gas Turbine Experiment and Research, 2017, 30 (1): 48–51. (in Chinese) |
| [4] |
吴秀宽, 林森. 某涡扇发动机风扇进口可调导流叶片调节规律分析[C]//第五届中国航空学会青年科技论坛文集(第5集). 北京: 北京航空航天大学出版社, 2012: 227-231.
WU X K, LIN S. The analyse about the control law of turbofan'IGV[C]//Proceedings of the Fifth China Aviation Society Youth Science and Technology Forum (Fifth Episodes). Beijing: Beihang University Press, 2012: 227-231(in Chinese). |
| [5] |
曹志鹏, 刘波, 丁伟. 静叶角度调节对组合压气机性能优化机理[J].
北京航空航天大学学报, 2007, 33 (8): 878–881.
CAO Z P, LIU B, DING W. Stator setting angles adjustment on performance improvement of axial-centrifugal compressor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33 (8): 878–881. (in Chinese) |
| [6] |
张健, 任铭林. 静叶角度调节对压气机性能影响的试验研究[J].
航空动力学报, 2000, 15 (1): 27–30.
ZHANG J, REN M L. Experimental investigation on effect of stator vane angle adjustment on compressor performance[J]. Journal of Aerospace Power, 2000, 15 (1): 27–30. (in Chinese) |
| [7] |
张宇飞, 么子云, 唐松林, 等. 一种基于主成分分析和支持向量机的发动机故障诊断方法[J].
中国机械工程, 2016, 27 (24): 3307–3311.
ZHANG Y F, YAO Z Y, TANG S L, et al. An engine fault diagnosis method based on PCL and SVR[J]. China Mechanical Engineering, 2016, 27 (24): 3307–3311. DOI:10.3969/j.issn.1004-132X.2016.24.008 (in Chinese) |
| [8] | BI F R, LIU Y P. Fault diagnosis of valve clearance in diesel engine based on BP neural network and support vector machine[J]. Transactions of Tianjin University, 2016, 22 (6): 536–543. DOI:10.1007/s12209-016-2675-1 |
| [9] |
殷锴, 钟诗胜, 那媛, 等. 基于BP神经网络的航空发动机故障检测技术研究[J].
航空发动机, 2017, 43 (1): 53–57.
YIN K, ZHONG S S, NA Y, et al. Research on aeroengine fault detection technology based on BP neural network[J]. Aeroengine, 2017, 43 (1): 53–57. (in Chinese) |
| [10] |
栾圣罡. 基于气路参数样本的航空发动机状态监视方法与系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
LUAN S G. Aeroengine condition monitoring technique and system based on gas path parameter sample[D]. Harbin: Harbin Institute of Technology, 2008(in Chinese). |
| [11] |
刘永建. 基于改进神经网络的民机发动机故障诊断与性能预测研究[D]. 南京: 南京航空航天大学, 2012.
LIU Y J. Research on modified neural network for fault diagnosis and performance prediction of aeroengine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). |
| [12] |
王芳. 基于支持向量机的沪深300指数回归预测[D]. 济南: 山东大学, 2015.
WANG F. CSI 300 index regression prediction based on support vector machine[D]. Jinan: Shandong University, 2015(in Chinese). |
| [13] |
史峰, 王辉, 郁磊, 等.
智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011.
SHI F, WANG H, YU L, et al. 30 cases analysis of intelligent algorithm[M]. Beijing: Beihang University Press, 2011. (in Chinese) |
| [14] |
崔智全. 民航发动机气路参数偏差值挖掘方法及其应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
CUI Z Q. Civil aeroengine gas path parameter deviation mining method with application[D]. Harbin: Harbin Institute of Technology, 2013(in Chinese). |
| [15] | Boeing. 777 aircraft maintenance manual[Z]. Chicago: Boeing, 2015. |
| [16] |
彭泽琰, 刘刚.
航空燃气轮机原理[M]. 北京: 国防工业出版社, 2000.
PENG Z Y, LIU G. Principles of aviation gas turbines[M]. Beijing: National Defense Industry Press, 2000. (in Chinese) |
| [17] | Pratt & Whitney Company. ECMⅡtraining manual[Z]. Hartford: Pratt & Whitney Company, 1994. |
| [18] |
周百政, 曹惠玲. 基于EHM软件思路的QAR数据处理[J].
航空维修与工程, 2010 (4): 60–62.
ZHOU B Z, CAO H L. QAR data processing based on the method of EHM software[J]. Aviation Maintenance & Engineering, 2010 (4): 60–62. (in Chinese) |



