随着控制过程复杂性的提高和对非线性问题认识的深入,非线性系统辨识越来越成为控制问题的关键。建立描述非线性现象的模型是研究非线性问题的基础,如Bilinear模型、Hammerstein模型、Wiener模型和输入输出仿射模型等[1-3]。但这些模型由于受到自身结构限制,只能描述部分特殊的非线性系统,所以一些普遍意义上的非线性模型相继被提出,如Volterra模型、NARMAX模型、神经网络模型、模糊逻辑模型、支持向量学习机模型和遗传规划(GP)模型等[4-11]。综观上述非线性模型,各有优势和不足,但其均可用非线性的线参数多项式组合模型来表示。国内外针对此类模型结构和参数的一体化辨识方法开展了一系列研究。文献[12]采用经典Gram-Schmidt(CGS)算法和改进Gram-Schmidt(MGS)算法对NARMAX模型进行子模型集合的选取;文献[13]采用新模型选项准则对NARMAX模型进行结构确定和参数估计研究;文献[14]采用前向正交最小二乘法(OLS)和误差衰减(ERR)准则对线参数非线性多项式模型进行结构预选;文献[15]提出自适应遗传算法与相关度评估结合方法对组合非线性系统进行结构和参数一体化辨识研究。文献[16]采用正交回归与嵌套最优正则化对一类非线性模型进行非线性辨识。
本文提出一种非线性多项式模型结构与参数一体化辨识策略。首先,采用递归改进Gram-Schmidt (RMGS)算法从向量空间的全集中执行“择优过程”,即寻找出一个能够描述输入输出映射关系的集合,该集合是包含核心结构项和少量冗余项的优选集。其次,在优选集合里执行“劣汰过程”,根据基于改进正交化次序的模型结构劣汰策略逐个删除对实际输出贡献相对较小的结构项,以系统完备性指标为约束,确认结构与参数。二者结合即为结构辨识与参数辨识的一体化方法,此方法避免了正交最小二乘法和前向逐步回归法在非线性系统辨识过程会漏选关联性结构项的问题。为方便对比分析,本文称该一体化方法为MTGS (Modified Total Gram-Schmidt)算法。
1 线参数多项式组合模型描述普适性的非线性系统有一大类可以用线参数多项式组合模型[15]来描述。这类模型通用表达式为
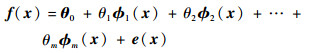
|
(1) |
式中:f(x)为模型输出, x为训练样本的输入向量;θ0为系统广义截距;θi(i=1, 2, …, m)为模型系数;ϕi(x)(i=1, 2, …, m)为多项式结构项;e(x)为干扰噪声。
若ϕi(x)∈u(k-j),j=1, 2, …, m,则模型为脉冲响应模型,u为与输入有关的结构项,k为采样时刻;若ϕi(x)∈{u(k-i), y(k-j)},i=0, 1, …, m1,j=1, 2, …, m2,则模型为AMAX模型,y为与输出有关的结构项;若ϕi(x)∈{y(k-j)},j=1, 2, …, m2,则模型为自回归(AR)模型;若ϕi(x)∈{u(j),u(j)u(k),u(j)u(k)u(l), …},j, k, l=1, 2, …, n,则模型为Volterra级数模型;若ϕi(x)∈{u(j), y(j), u(j)u(k), u(j)y(k), y(j)y(k), …},j, k=1, 2, …, n,则模型为非线性NARMAX模型;若ϕi(x)∈{K(x, x1), K(x, x2), …, K(x, xl), b},其中x1, x2, …, xl为l个训练样本,K(·)为样本输入的非线性映射,则模型为基于核函数映射的非线性模型,b为常数;若ϕi(x)∈{(x, cos x, ex, ln x, …),[+, /, ∑·, …]},其中(·)为对输入向量非线性描述,[·]为非线性运算符,则模型为非线性多项式组合模型。
在辨识过程中,首先对数据进行中心化处理,消除广义截距对结构项的共线性影响。根据实际N个采样点数据,式(1)转化为
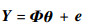
|
(2) |
式中:Y=[y(x1), y(x2), …, y(xN)]T;θ=[θ1, θ2, …, θm]T;e=[e(x1), e(x2), …, e(xN)]T;Φ=[ϕ1, ϕ2, …, ϕm]N×m, i=1, 2, …, N, N≥m。
任何系统在其寿命范围内,严格非时变情况是不存在的,因此多项式系数也是时变的。为有效观测或控制一个系统,本文以非线性时变多项式模型为研究对象,开展模型结构与参数的一体化辨识研究。
2 基于向量空间投影理论的正交化分析非线性多项式模型结构辨识问题的关键在于如何从一个满覆盖的空间集合Vm中寻找一个次优且满足精度的子空间集合Vr,r≤m是有界但未知。
引理1[17] Y(V)为向量Y在空间V的投影,其与向量Y夹角为β,投影残差为δYV,且满足: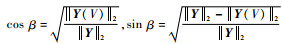
定理1 假定由张成的满空间为Vm=span{ϕ1, ϕ2, …, ϕm},任意的Vr=span{ϕ1, ϕ2, …, ϕr},Vr-1=span{ϕ1, ϕ2, …, ϕi-1, ϕi+1, …, ϕr}。记向量Y在满空间的投影为Y(Vm),在Vr空间与Vr-1空间的投影分别为Y(Vr)与Y(Vr-1),投影残差分别为δYVr与δYVr-1,且分别满足δYVr⊥Vr,δYVr-1⊥Vr-1。记向量ϕi在Vr-1空间的投影为ϕi(Vr-1),在Vr-1空间的投影残差δϕiVr-1=ϕi-ϕi(Vr-1),且满足δϕiVr-1⊥Vr-1;则有如下结论:
1) Y(Vr)=Y(Vr-1)+δYVr-1δϕiVr-1。
2) ||Y(Vr)||2=||Y(Vr-1)||2+||δYVr-1δϕiVr-1||2。
证明 结论1)的证明:
由Vr=Vr-1+span(δϕiVr-1), 得Y(Vr)=Y(Vr-1+span(δϕiVr-1))=Y(Vr-1)+YδϕiVr-1;又由Y(Vr-1)⊥span(δϕiVr-1),span(δϕiVr-1)⊥Vr-1,Vr-1⊥δϕiVr-1得Y(Vr-1)⊥δϕiVr-1;即YδϕiVr-1=YδϕiVr-1-Y(Vr-1)·δϕiVr-1=δYVr-1δϕiVr-1。故Y(Vr)=Y(Vr-1)+δYVr-1δϕiVr-1。
结论2)的证明:
由Vr-1⊥δϕiVr-1,得||Y(Vr)||2=||Y(Vr-1)||2+||YδϕiVr-1||2=||Y(Vr-1)||2+||δYVr-1δϕiVr-1||2。 证毕
定理1揭示了向量在空间的投影与残差在空间的投影之间的对应关系。由定理1可得以下2条推论:
推论1 δYVr=δYVr-1-δYVr-1δϕiVr-1。
推论2 ||δYVr||2=||δYVr-1||2(1-cos2(δϕiVr-1, δYVr-1))。
证明 推论1的证明:
由δYVr=Y-Y(Vr)=Y-(Y(Vr-1)+Y·δϕiVr-1)=δYVr-1-YδϕiVr-1;又Y(Vr-1)⊥δϕiVr-1得δYVr=δYVr-1-YδϕiVr-1+Y(Vr-1)δϕiVr-1=δYVr-1-δYVr-1δϕiVr-1。
推论2的证明:
由||δYVr||2=||δYVr-1-δYVr-1δϕiVr-1||2=(δYVr-1)2-2δYVr-1(δYVr-1δϕiVr-1)+(δYVr-1δϕiVr-1)2和Y-Y(Vr)=δYVr, Y-Y(Vr-1)=δYVr-1,得δYVr-1=Y(Vr)+δYVr-Y(Vr-1)=δYVr-1δϕiVr-1+δYVr;又由δYVr-1δϕiVr-1∈Vr, δYVr⊥Vr得δYVr⊥δYVr-1δϕiVr-1;所以δYVr-1(δYVr-1δϕiVr-1)=(δYVr+δYVr-1δϕiVr-1)(δYVr-1δϕiVr-1)=(δYVr-1δϕiVr-1)2。故||δYVr||2=||δYVr-1||2-||δYVr-1δϕiVr-1||2=||δYVr-1||2(1-||δYVr-1δϕiVr-1||2/||δYVr-1||2)=δYVr-1||2(1-cos2(δYVr-1, δϕiVr-1))。 证毕
推论描述了向量在空间的投影残差之间的递推关系。
正交化算法有2个功能[18]:①将变量集合中的信息进行正交分解;②排除ϕ1,ϕ2,…,ϕm中的冗余变量(即被变换成0的变量)。由于这m个向量非正交,为求解模型系数θ,需对其正交化得到正交空间及向量Y在正交空间的投影。而误差就产生在上述过程中。
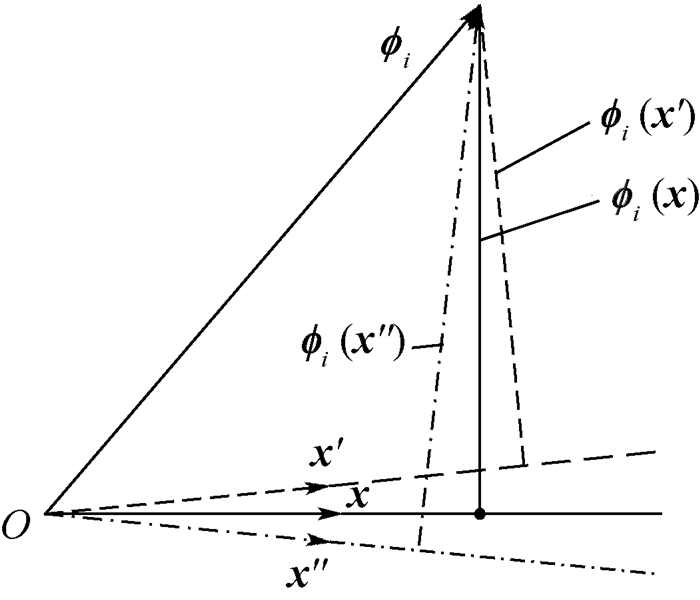
由推论可知,正交化次数越多,正交化向量范数越小,舍入误差对正交化进程的影响越大。因此CGS算法[12]每一次迭代都是原始向量ϕi相对前面已正交化小向量的正交化,即“大向量面向小向量正交化”的过程,故误差较大,如图 1所示,其中x、x′、x″为正交空间的正交向量。
|
| 图 1 大向量正交误差传播 Fig. 1 Orthogonal error propagation of large vectors |
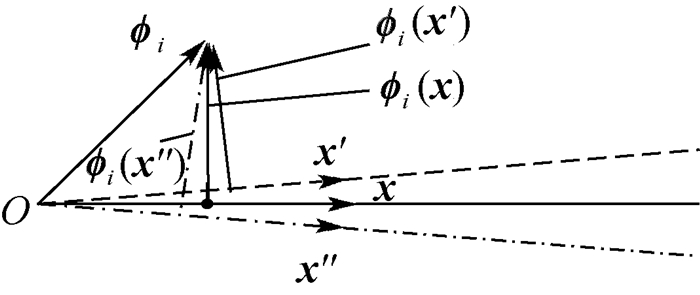
MGS算法[12]由于每一次迭代选择的向量是ϕik而非原始向量。而ϕik的获得是基于原始向量已正交化后的向量,可理解为“小向量面向小向量正交化”的过程,故误差较小,如图 2所示。
|
| 图 2 小向量正交误差传播 Fig. 2 Orthogonal error propagation of small vectors |
综上,正交化过程选择不同,直接导致计算误差的不同传递,造成计算结果变差甚至错误,此现象在大矩阵计算中尤为明显。以上2种算法未对正交化向量选择次序进行处理,计算中仍可能出现“大向量面向小向量正交化”的过程。考虑到正交化次序对输出向量残差化的影响,本文提出非线性多项式模型结构和参数一体化辨识方法。
3 多项式模型的结构和参数一体化辨识 3.1 模型结构优选分析与停止条件由推论1和2可知:①随着正交化次数的增多,输出向量的投影残差模越来越小,最终趋于噪声化;②在正交化过程中,输出向量残差模在某些项时其二阶范数迅速递减。分析可知,下降较大时对应为模型结构项。若正交化过程中执行一种残差监视线程,则可区分这些结构项,实现多项式模型的结构辨识。
改善这种投影有2种思路:①在每一步投影时,向与输出残差相关度最大的向量投影;②采用向二阶范数最大的基向量投影。思路①的风险在于:若范数小,正交化残差偏差较大;思路②的风险在于:若范数大,但有可能不是结构项,且增加了正交化次数。因此,本文折中选择某一项使得输出残差向量范数下降最快,这样迭代过程就较快实现输出向量残差的噪声化。
针对线参数模型式(2),根据QR分解有eN×1=Y-Φθ=Y-QRθ=Y-QG,其中:Q=[q1, q2, …, qm]N×m,Rm×m为对角线为1的上三角矩阵。数学上为方便求解,设D=QTQ=diag[d1, d2, …, dm],经过对输出向量Y的处理可得m维实向量,即G=D-1QTY;然后针对Rθ=G回代计算求解。对Y=QG+eN×1两边取二阶范数的平方得
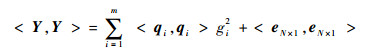
|
(3) |
将式(3)变形可得
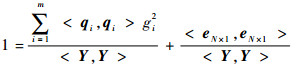
|
(4) |
因此,若在选项中选择对应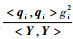
1) 监视残差比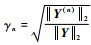
2) 监视残差化输出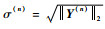
在MGS算法基础上提出RMGS算法,即采用选择主元策略,调整正交化次序,使得正交化过程的误差影响最小。
原先的正交化待选项为Φ=[ϕ1, ϕ2, …, ϕm]和Q=[q1, q2, …, qm],对应的解为θ,原先解的序号对应为λ(0, :)=[1, 2, …, m]。
记重新选择的正交化矩阵为Φnew=[ϕ1, new, ϕ2, new, …, ϕm, new]和Qnew=[q1, new, q2, new, …, qm, new],对应的解为θnew,选主元后的序号为λ(m, 1), λ(m, 2), …, λ(m, m)。
RMGS算法的迭代流程如下:
步骤1 记ϕj0=ϕj, j=1, 2, …, m;记Y(0)=Y;记q1i=ϕi0, i=1, 2, …, m。计算:d1i= < q1i, q1i>;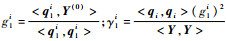
假设d1i1=max{γ1i, 1≤i≤m},记q1, new=q1i1并作为Qnew的第1列。分别计算g1, new=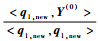
执行一个提取过程:for i=1:k-1,有Ri, 1new⇐αnewi, i1。即将前面i=1~(k-1)步骤中得到的αinew第i1列元素作为Rnew的第1列元素,以确保回归迭代过程中结构向量与系数是对应的。
计算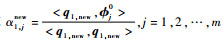
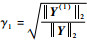
步骤k 1 < k≤m:此时i=1, 2, …, m,j∉{i1, i2, …, i(k-1)};记qki=ϕik-1,计算dki= < qki, qki>,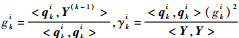
假设dkik=max{γki, k≤i≤m},记qk, new=qkik并作为Qnew的第k列。分别计算gk, new=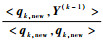
执行一个提取过程:for i=1:k-1,有Ri, knew⇐αnewi, ik。即将步骤i(i=1, 2, …, k-1)中得到的αinew第ik列元素作为Rnew的第k列元素,确保回归迭代过程中结构向量与系数是对应的。
计算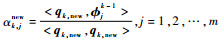
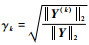
如果k≥m或者γk < ε,ε为阈值,则跳出循环,给出模型重要结构项系数的序号λ=[i1, i2, …, ik],进入步骤Last;否则迭代循环。
步骤Last 至此已得到Gnew和Rnew,其中:
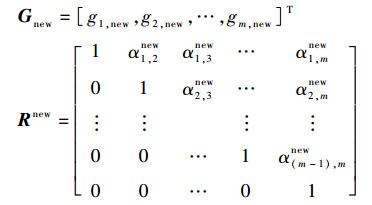
|
对Rnewθnew=Gnew回代,回代结果对应序号{λ(1), λ(2), …, λ(m-1)}的原始结构项系数。
3.3 基于改进正交化次序模型结构劣汰策略由第2节可知,后期正交化过程会产生较大误差。在此过程中,选项个数仍记为m个,原始输入向量矩阵的重新排列为Φnew=[ϕλ(1), ϕλ(2), …, ϕλ(m)],其正交化矩阵Qnew=[q1, new, q2, new, …, qm, new]中第i个向量qi, new相对于q1, new, q2, new, …, qi-1, new是正交的,但相对于后面向量的正交化程度是不均等的。为平等对待正交化向量,将结构项顺序重新排列,每一向量分别最后正交化,并计算其贡献,再根据贡献大小排序,实现“平等”劣汰过程。
针对ϕλ(i),重新排列Φnewi=[ϕλ(1), ϕλ(2), …, ϕλ(i-1), ϕλ(i+1), …, ϕλ(m)],记Qnewi=[q1, new, q2, new, …, qi-1, new, q′i+1, new, …, q′m, new, q″i, new],故ϕλ(i)相对于ϕλ(1), ϕλ(2), …, ϕλ(i-1), ϕλ(i+1), …, ϕλ(m)对描述Y的贡献为C(λ(i))=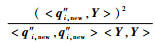
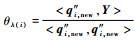
对Qnewi的求解可重新执行一次正交化过程,但会占用大量计算资源。考虑到上述迭代过程中已进行正交化,因此通过适当的变形即可求出Qnewi。下面给出推理过程:
在已正交化过程中,以第i个向量qi, new为例,其后续向量为qi+1, new;进行重新排列后,得到的q′i+1, new相对qi+1, new少执行了一次针对qi, new的正交化过程。因此:q′i+1, new-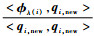
依次类推,其后面的向量q′i+2, new, q′i+3, new, …, q′m, new相对qi+2, new, qi+3, new, …, qm, new都少执行了一次针对qi, new的正交化过程。因此,q′j, new=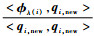
同理,由于第i个向量在重排后放置于最后位置的q″i, new,其相对于原始向量增加了针对q′i+1, new, q′i+2, new, …, q′m, new的正交化过程。故可得其推理过程:
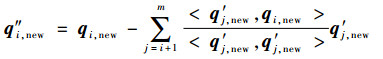
|
(5) |
综上,上述推理方法可减少求解Qnewi时,再次正交化的全部计算量。分别对每个向量重新排列,使每个候选项在正交化过程中受到的误差影响是一致的,然后在这种一致的基础上,删除贡献较小的项,谨慎地保护了结构项不易漏选。单纯的劣汰过程也可针对特征项的全集进行,但需要注意某些项在计算过程会出现 < q′j, new, q′j, new>接近于零,此时需将该项删除,避免数值计算病态问题。
4 仿真算例为说明MTGS算法的有效性,以2个典型算例为研究对象,将MTGS算法与CGS算法、MGS算法进行仿真对比。给出了MTGS算法详细仿真步骤,限于篇幅对CGS算法和MGS算法只给出仿真对比结果。
4.1 算例1非线性多项式模型——Volterra模型设定三阶脉冲响应输入输出表达式

|
(6) |
式中:e(k)为白噪声干扰信号,噪信比为0.1;一、二、三阶时延分别为d1=5、d2=5和d3=2。
在对上述模型进行辨识前,认为对系统的输入输出关系有一定了解,预先假定系统为一个阶次为3的非线性多项式模型,其中一阶时延为10,二阶时延为7,, 三阶时延为5,共含有C101+(C72+C71)+(C53+C51C41)+C51=73个结构项(包含了系统式(6)的核心结构项)。此时问题转化为如何从这些结构项集合中选择结构并辨识参数。
由排列顺序可假定系统的结构项为:ϕ1=u(k-1), …, ϕ10=u(k-d1), ϕ11=u(k-1)2, …, ϕ17=u(k-1)u(k-d2), …, ϕ38=u(k-d2)2, …, ϕ39=u(k-1)3, ϕ40=u(k-1)2u(k-2), …, ϕ73=u(k-d3)3。
由采样点数N(N>73),可计算73个结构项分别对应的N个采样数据,并组成矩阵xϕ1=[u(k), u(k+1), …, u(k+N-1)]T,xϕ2=[u(k-1), u(k), …, u(k+N-2)]T,…,xϕ73=[u(k-d3+1)3, u(k-d3+2), …, u(k-d3+N)3]T,Y=[y(k+1), y(k+2), …, y(k+N)]T。根据排列可知:系统的实际结构项对应为ϕ1, ϕ2, ϕ3, ϕ5, ϕ11, ϕ12, ϕ13, ϕ19, ϕ24, ϕ26, ϕ40。
辨识步骤如下:
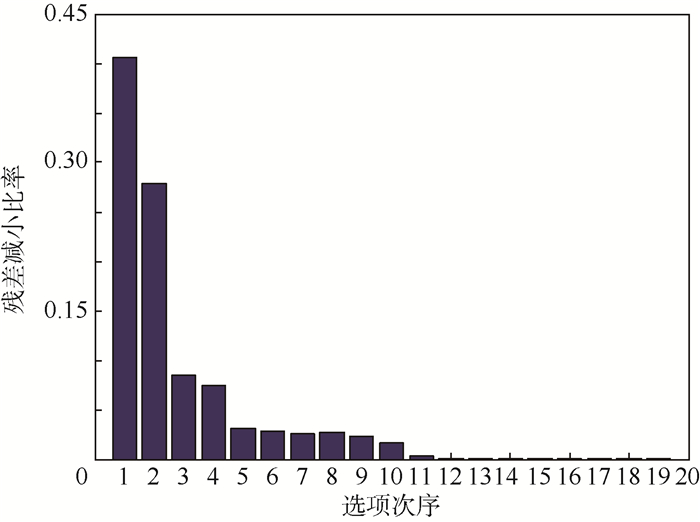
步骤1 择优过程残差减小比率如图 3所示,共筛选出19项,图中序号1~19对应为2、1、24、3、40、11、12、13、26、19、5、28、21、66、39、17、34、68、8;基本上前面11项对应系统式(6)实际结构项,但由于择优过程需要保持一定的冗余度,故多选择了部分项。
|
| 图 3 残差减小比率(算例1) Fig. 3 Residual decrease ratio (Example 1) |
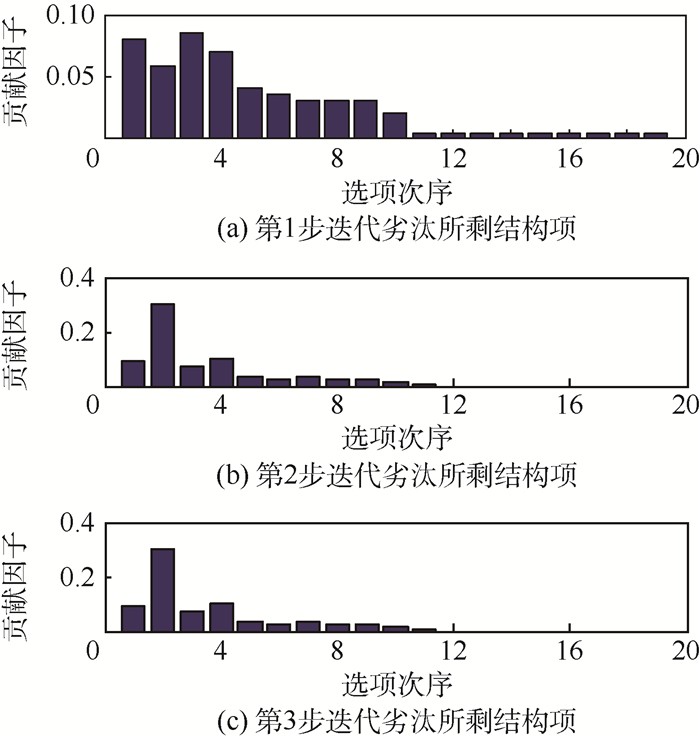
步骤2 劣汰过程贡献因子变化如图 4所示。图 4(a)、(b)、(c)依次表示算法每一步迭代后淘汰贡献因子小的结构项的动态过程。可见每一项的贡献在正交化顺序不同时发生了变化,因此劣汰过程中采取的方式对每一个向量都是公平的;在劣汰过程,通过2步迭代就达到了满意度。系统值与3种算法辨识的结构项及对应参数值的对比如表 1所示。
|
| 图 4 贡献因子变化(算例1) Fig. 4 Change of contribution factor (Example 1) |
| 模型 | ϕ2 | ϕ1 | ϕ24 | ϕ3 | ϕ40 | ϕ11 | ϕ12 | ϕ13 | ϕ26 | ϕ19 | ϕ5 |
| 实际模型 | 0.8 | 1.0 | -1.8 | 0.5 | 4.6 | 1.0 | 1.0 | 1.0 | 1.0 | 0.8 | -0.1 |
MTGS算法 辨识模型 | 0.844 2 | 0.997 1 | -1.706 9 | 0.496 7 | 4.633 4 | 0.982 5 | 1.015 3 | 0.998 5 | 1.000 0 | 0.798 7 | -0.101 5 |
| CGS算法 辨识模型 | 0.879 3 | 1.055 6 | -1.706 9 | 0.526 5 | 4.181 2 | 0.894 6 | 0.993 0 | 0.988 3 | 1.020 5 | 0.786 9 | -0.054 9 |
| MGS算法 辨识模型 | 0.874 2 | 0.993 8 | -1.775 9 | 0.496 2 | 4.636 4 | 1.007 7 | 1.003 3 | 0.984 9 | 0.994 4 | 0.810 2 | -0.106 3 |
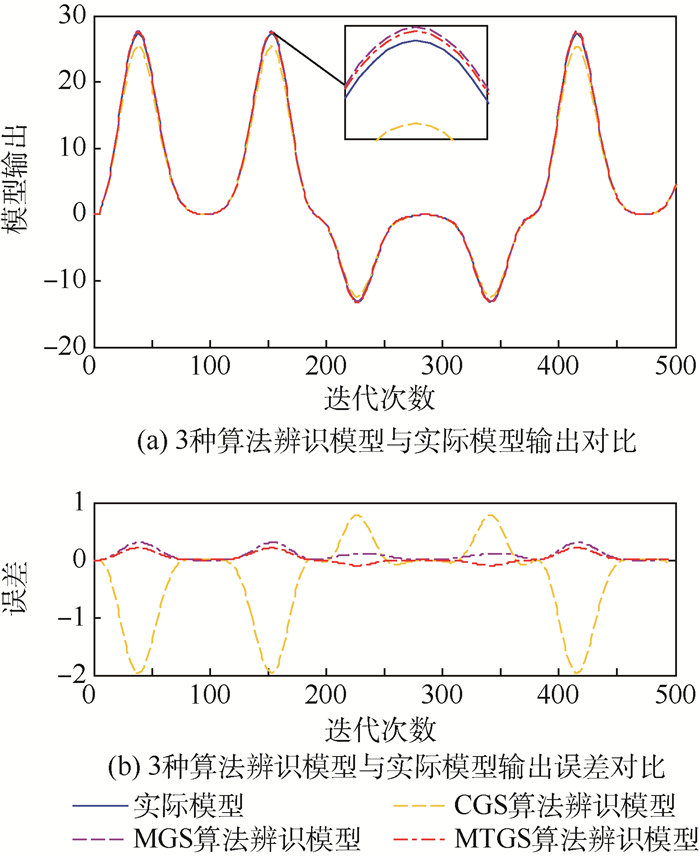
设输入u(k)=sin (k/20)+sin (k/60),k=1, 2, …, 500,设置初始时刻值为y(1)=y(2)=y(3)=0.01。图 5所示为实际模型输出与3种算法辨识模型输出的仿真对比。
|
| 图 5 辨识模型与实际模型仿真对比(算例1) Fig. 5 Comparison of identifiation model and actual modelsimulation(Example 1) |
非线性多项式模型——NARMAX模型系统的结构选择如下模型
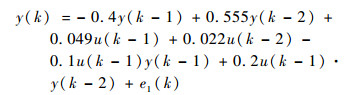
|
(7) |
式中: e1(k)为输入信号强度的1/50随机信号。为了验证方法,预先假定系统为一个阶次为2的非线性多项式模型,其中u(k)与y(k)的时延均为3,共含有C3+31+C3+31+C3+32=27个结构项(包含了系统式(7)的核心结构项)。由排列顺序可假定系统的结构项为:ϕ1=u(k-1), …, ϕ3=u(k-3), ϕ4=y(k-1), …, ϕ6=y(k-3),…,ϕ7=u(k-1)2, …, ϕ10=u(k-1)u(k-3), …, ϕ13=u(k-3)2, …, ϕ14=y(k-1)2, …, ϕ27=y(k-3)2。根据采样点数N(N>27),可计算27个结构项分别对应的N个采样数据,原理同算例1,不在赘述。此时问题转化为如何从这些结构项集合中选择结构并辨识参数。
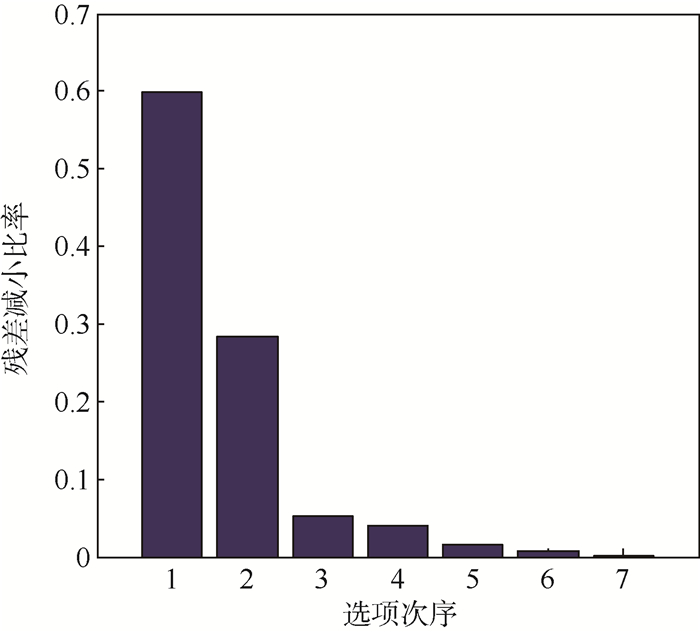
步骤1 择优过程残差减小比率如图 6所示,共筛选出7项,图中选项次序1~7分别为5、11、4、1、10、2、22项,包含了系统结构项。
|
| 图 6 残差减小比率(算例2) Fig. 6 Residual decrease ratio (Example 2) |
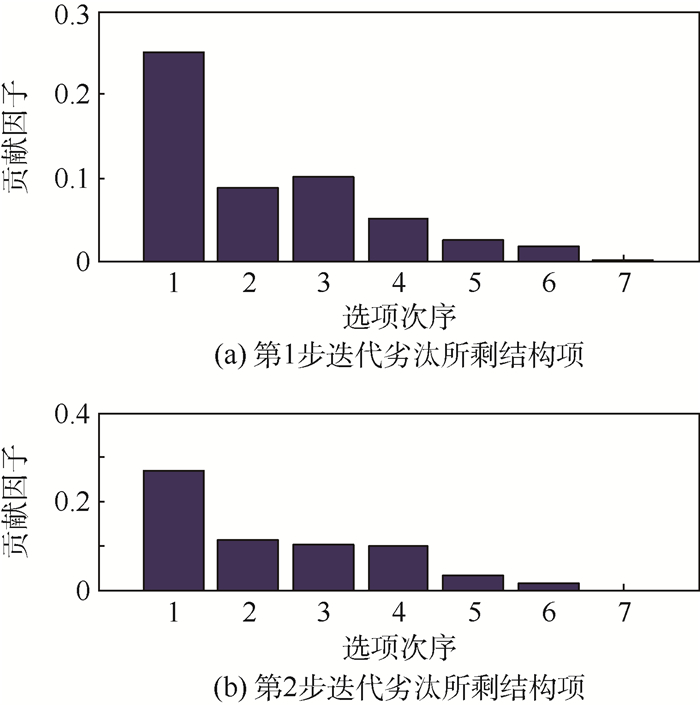
步骤2 劣汰过程贡献因子变化如图 7所示。2个分图依次表示算法每一步迭代淘汰贡献因子小的结构项的动态过程。删除了第22结构项,剩下前6项,即正确的结构项,同时得到结构项对应系数,见表 2。上述结构辨识,虽然结构辨识正确,但辨识的参数仍存在不足(如第1项),见表 2。分析原因,笔者认为是采样数据奇异或误差的吸收造成的;重新对数据进行处理后产生第2次仿真数据,进行系统结构与参数辨识,其过程如下:
|
| 图 7 贡献因子变化(算例2) Fig. 7 Change of contribution factor (Example 2) |
| 模型 | ϕ5 | ϕ11 | ϕ4 | ϕ1 | ϕ10 | ϕ2 |
| 实际模型 | 0.555 | 0.2 | -0.4 | 0.049 | -0.1 | 0.022 |
| MTGS算法辨识模型 | 0.567 1 | 0.199 8 | -0.397 8 | 0.048 9 | -0.100 0 | 0.022 0 |
| CGS算法辨识模型 | 0.562 950 | 0.199 490 | -0.369 880 | 0.049 000 | -0.100 180 | 0.020 574 |
| MGS算法辨识模型 | 0.543 270 | 0.200 060 | -0.429 500 | 0.048 992 | -0.099 997 | 0.023 458 |
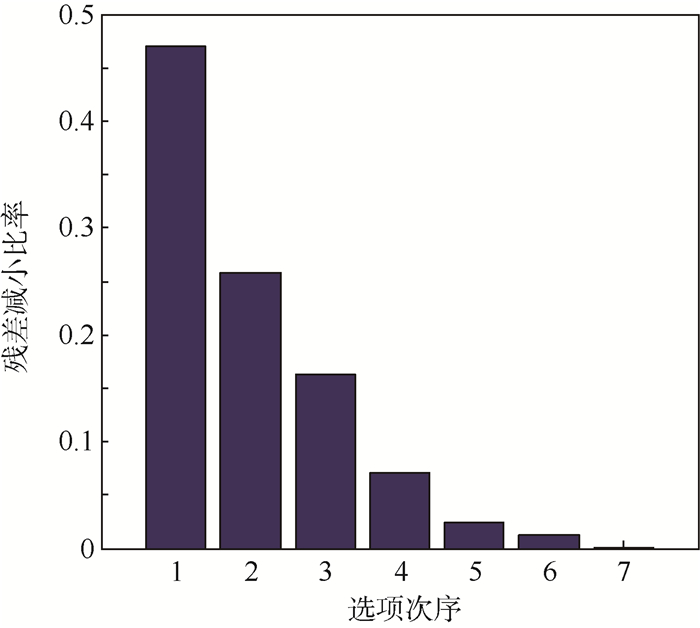
步骤1 择优过程残差减小比率如图 8所示。该步骤中选出了7项,图中选项次序1~7分别为4、11、5、1、10、2、18项,包含了系统结构项。
|
| 图 8 残差减小比率(算例2第2次仿真数据) Fig. 8 Residual decrease ratio (data in the second simulation for Example 2) |
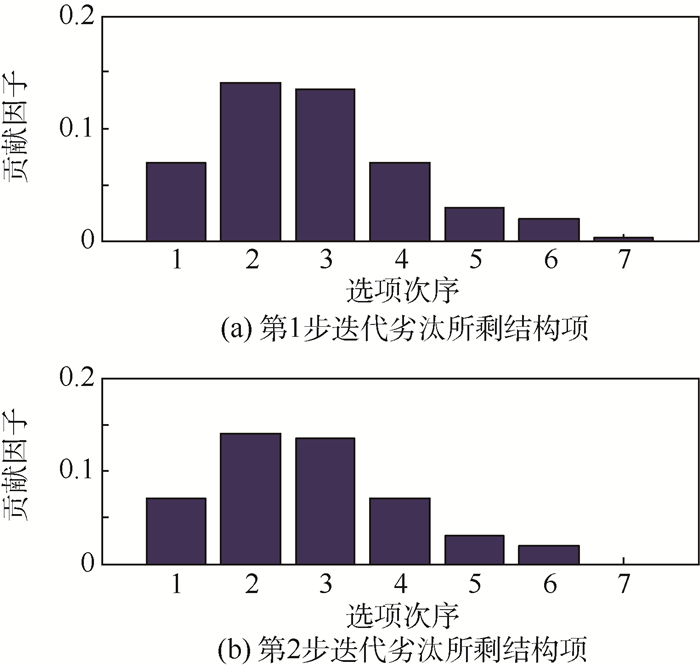
步骤2 劣汰过程贡献因子变化如图 9所示。图 9(a)、(b)依次表示算法每一步迭代淘汰贡献因子小的结构项的动态过程。删除了第18项后,只剩下6项,即正确的结构项,对应参数如表 3所示。这个过程的结构辨识正确,参数偏差相对前次较小,可看出正交化次序的不同会对辨识结果有影响。
|
| 图 9 贡献因子变化(算例2第2次仿真数据) Fig. 9 Change of contribution factor (data in the second simulation for Example 2) |
| 模型 | ϕ4 | ϕ11 | ϕ5 | ϕ1 | ϕ10 | ϕ2 |
| 实际模型 | -0.4 | 0.2 | 0.555 | 0.049 | -0.1 | 0.022 0 |
| MTGS算法辨识模型 | -0.391 7 | 0.208 8 | 0.554 8 | 0.048 9 | -0.100 0 | 0.022 0 |
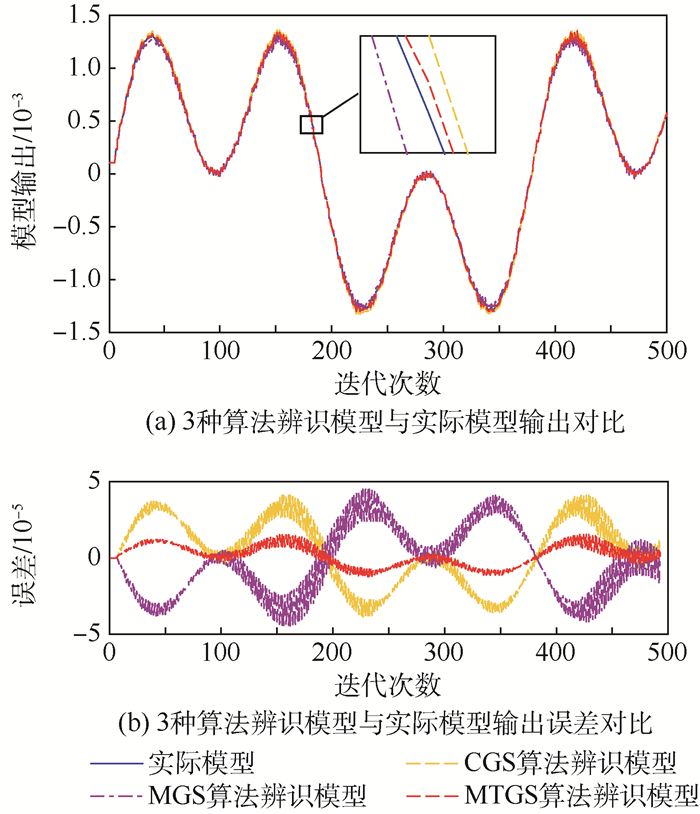
设输入为u(k)=0.001(rand-0.5)+0.01·(sin(k/60)+sin(k/20)),k=1, 2, …, 500,初始时刻值y(1)=y(2)=y(3)=0.000 1。图 10为实际模型与3种算法辨识模型的仿真输出对比。
|
| 图 10 辨识模型与实际模型仿真对比(算例2) Fig. 10 Comparison of identification model and actual model simulation (Example 2) |
本文提出了一种非线性多项式模型结构和参数辨识方法,该方法包含基于贡献项的“择优过程”与基于冗余项的“劣汰过程”,研究了线参数多项式组合模型的结构与参数一体化辨识:
1) 采用RMGS算法可以从一个满覆盖的向量空间集合Vm中寻找出一个次优且满足精度需求的子空间集合Vr。
2) 基于改进正交化次序的模型结构劣汰策略,在包含核心结构项和少量冗余项的优选集中筛选出对实际输出贡献相对较小的结构项,以系统完备性指标为约束,确认了系统模型的结构与参数,稳妥地保护了随正交化次数增加可能会漏选的非显著模型项。
3) 对2个典型的非线性多项式模型进行仿真验证。无论从辨识模型的模型系数还是基于辨识模型的再次仿真对比结果,都说明MTGS算法比CGS算法和MGS算法更具有效性且计算时间短。
4) 需要说明的是,合理地定量选择阈值仍需进一步研究。若设置过大,则会将某些微弱贡献项漏选;若设置过小,则又可能无端增加迭代次数,增加计算时间。
| [1] | DING F, LIU X P, LIU G. Identification methods for Hammerstein nonlinear systems[J]. Digital Signal Processing, 2011, 21 (2): 215–238. DOI:10.1016/j.dsp.2010.06.006 |
| [2] | RUGH W J. Nonlinear system theory-The Volterra Wiener approach[M]. Baltimore: Johns Hopkins University Press, 1981: 412-414. |
| [3] | LEONTARITIS I J, BILLINGS S A. Input-output parametric models for nonlinear system, part:Stochastic nonlinear system[J]. International Journal of Control, 1985, 41 (2): 1863–1878. |
| [4] | CHEN S, BILLINGS S A, GRANT P M. Non-linear system identification using neural networks[J]. International Journal of Control, 1990, 51 (6): 1191–1214. DOI:10.1080/00207179008934126 |
| [5] |
欧文, 韩崇昭, 王文正. Volterra泛函级数在非线性系统辨识中的应用[J].
控制与决策, 2002, 17 (2): 239–242.
OU W, HAN C Z, WANG W Z. Application of Volterra series in the identification of nonlinear system[J]. Control and Decision, 2002, 17 (2): 239–242. (in Chinese) |
| [6] | SUGENO M, KANG G. Structure identification of fuzzy model[J]. Fuzzy Sets and Systems, 1988, 28 (1): 15–33. DOI:10.1016/0165-0114(88)90113-3 |
| [7] |
李应红, 尉询楷, 刘建勋.
支持向量机的工程应用[M]. 北京: 国防工业出版社, 2004: 44-50.
LI Y H, YU X K, LIU J X. Engineering application of support vector machines[M]. Beijing: National Defense Industry Press, 2004: 44-50. (in Chinese) |
| [8] | KOZA J R. Genetic programming:On the programming of computers by means of natural selection[M]. Cambridge: MIT Press, 1992: 23-25. |
| [9] |
周霞, 沈炯. 多目标免疫GEP算法及其在多项式NARMAX模型辨识中的应用[J].
控制与决策, 2014, 29 (6): 1009–1015.
ZHOU X, SHEN J. A immune based multiobjective GEP algorithm for identifying polynomial NARMAX model[J]. Control and Decision, 2014, 29 (6): 1009–1015. (in Chinese) |
| [10] |
程长明. 基于Volterra级数的非线性系统辨识及应用研究[D]. 上海: 上海交通大学, 2015: 98-120.
CHENG C M. Nonlinear system identification and application based on Volterra series[D]. Shanghai: Shanghai Jiao Tong University, 2015: 98-120(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10248-1016787797.htm |
| [11] |
陈森林, 高正红. 基于多小波展开的Volterra级数非线性系统建模方法[J].
西北工业大学学报, 2017, 35 (3): 428–434.
CHEN S L, GAO Z H. Nonlinear system modeling using multi-wavelet expansion based Volterra series[J]. Journal of Northwestern Polytechnical University, 2017, 35 (3): 428–434. (in Chinese) |
| [12] | CHEN S, BILLINGS S A, LUO W. Orthogonal least squares methods and their application to nonlinear system identification[R]. Sheffield: The University of Sheffield, 1988. |
| [13] |
王晓, 谢剑英, 贾青. 非线性NARMAX模型结构与参数一体化辨识的改进算法[J].
信息与控制, 2000, 29 (2): 102–110.
WANG X, XIE J Y, JIA Q. New modified integrated algorithm for structure determination and parameter estimation for nonlinear stochastic systems[J]. Information and Control, 2000, 29 (2): 102–110. (in Chinese) |
| [14] | WEI H L, BILLINGS S A, LIU J. Term and variable selection for nonlinear system identification[R]. Sheffield: The University of Sheffield, 2003. |
| [15] |
翟旭升, 王海涛, 谢寿生, 等. 基于自适应遗传算法的多项式模型结构与参数一体化辨识[J].
控制与决策, 2011, 26 (5): 761–767.
ZHAI X S, WANG H T, XIE S S, et al. Polynomial model structure and parameter integration identification based on adaptive genetic algorithm[J]. Control and Decision, 2011, 26 (5): 761–767. (in Chinese) |
| [16] | HONG X, CHEN S, GAO J. Nonlinear identification using orthogonal forward regression with nested optimal regularization[J]. IEEE Transactions on Cybernetics, 2015, 45 (12): 2925–2936. DOI:10.1109/TCYB.2015.2389524 |
| [17] |
龚怀云, 寿纪麟, 王锦森.
应用泛函分析[M]. 西安: 西安交通大学出版社, 1995: 160-178.
GONG H Y, SHOU J L, WANG J S. Applied functional analysis[M]. Xi'an: Xi'an Jiaotong University Press, 1995: 160-178. (in Chinese) |
| [18] |
王惠文, 夏棒. 快速Gram-Schmidt回归方法[J].
北京航空航天大学学报, 2013, 39 (9): 1259–1262.
WANG H W, XIA B. Quick Gram-Schmidt regression method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39 (9): 1259–1262. (in Chinese) |



