金属材料的疲劳是各类机械结构中的常见失效形式[1-2]。承受循环载荷的受力构件易在初始缺陷或应力集中处萌生裂纹,裂纹逐渐扩展使得结构丧失承载能力最终导致破坏。材料的疲劳在没有产生宏观裂纹之前都难以观测,一旦产生了宏观裂纹之后,其损伤的发展速度会很快加速,在工程上会导致严重的后果[3]。目前工程上通过统计学与实验的结合,已经形成了一种较为成熟,适用性较强的一套理论方法,可以对工程件的寿命进行预测分析。通常是通过大量的疲劳损伤实验,拟合得到材料的S-N曲线,再通过力学分析计算结构的疲劳寿命[4]。
损伤力学将疲劳过程中的裂纹萌生视为一个渐进损伤的过程[5]。认为材料在交变载荷下,在微观层次上出现微缺陷,这些微缺陷的发展导致了局部宏观力学性能的变化。在微缺陷生长到一定程度后,此处便出现了宏观裂纹。损伤力学方法用热力学方法描述此不可逆的过程,通过定义损伤度场来刻画局部微缺陷的危险程度,并推导损伤演化方程表征其演化规律[6-7]。
损伤演化方程通常是描述损伤度累积速率的函数形式,其中损伤参数是代表材料损伤性能特征的材料参数。一般地,损伤演化参数多于一个,即会有2个或者更多的损伤演化参数,这些参数大多数都是通过实验决定。最常用的方法是通过S-N曲线决定参数,这些参数无法直接获得,而是采用参数拟合的方式进行估算,多参数拟合的方法计算量大,并且过程较为复杂,为结果带来一定的不确定性[8-14]。
本文研究目的是提出一种损伤演化方程参数确定的新方法,推导出充分利用实验数据,减少同时拟合参数个数,逐一确定损伤演化参数。
1 损伤演化方程首先,根据损伤力学理论[5, 8],对于各向同性金属材料,定义损伤度D为

|
(1) |
式中:E为材料的弹性模量;ED为材料损伤后微缺陷造成的有损弹性模量。显然损伤度D的取值范围为0~1。当D=0时,材料无损;当D=1时,材料局部失去承载能力,产生宏观裂纹。
材料含损伤的本构方程可以表示为
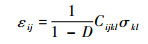
|
(2) |
式中:εij为应变分量;σkl为应力分量;Cijkl为四阶柔度张量。
损伤驱动力Y可定义为[8]
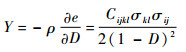
|
(3) |
式中:ρ为材料密度;e为应变能密度。
此时,损伤演化方程可以表示为[9]

|
式中:N为交变载荷循环次数;Yth为损伤驱动力门槛值;YM为相应于载荷峰值的损伤驱动力;Ym为载荷谷值的损伤驱动力;α和p为待定的材料常数。
特别地,对于单轴加载情况,由式(3)知:
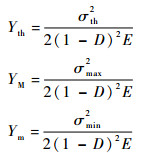
|
式中:σth为损伤应力门槛值;σmax为载荷应力峰值;σmin为载荷应力谷值。当Yth>Ym时,损伤演化方程简化为
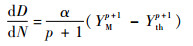
|
(4) |
代入单轴加载损伤驱动力表达式得
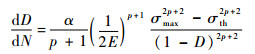
|
(5) |
一般通过式(5)的积分形式建立载荷与寿命的关系。然后利用标准疲劳实验数据对α和p这2个参数进行最小二乘法同时拟合,这种“多参数直接拟合”计算量大,对于误差十分敏感,给疲劳问题的计算带来了不必要的麻烦。
2 参数确定新方法 2.1 损伤参数p的确定对式(5)进行积分得

|
(6) |
式(6)等号左边取D=0和D=1为积分上下限定积分可得
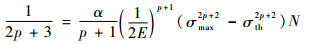
|
(7) |
观察式(7)右边非常数项,其乘积为一常量,当最大应力σmax产生微小增量Δσmax时,相应的循环次数N也将产生相应的微小负增量ΔN,即
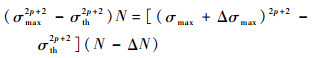
|
(8) |
泰勒展开式(8)右边项,消去高阶小量
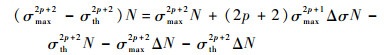
|
(9) |
整理式(9)并取极限可得
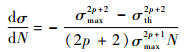
|
(10) |

|
(11) |
式(10)和式(11)中仅有一个未知材料损伤参数p,令对应的损伤度为1,式(10)即为S-N曲线上一点(σmax,N)的斜率,损伤参数p即可基于实验的S-N曲线通过式(10)确定。
基于材料疲劳寿命的分散性和实验误差,可在S-N曲线上取多组中值疲劳实验数据点(σmaxi,Ni),对式(10)两边取对数并整理后得

|
(12) |
进一步,定义参数拟合均方差函数为

|
(13) |
一般认为损伤参数p为材质参数,与载荷无关,故对于特定S-N曲线,p为常数。因此,p的取值应使其拟合均方差取得极小值,即

|
(14) |
至此,综合式(10)~式(14)可计算出p值,从而实现损伤参数的单一确定。
2.2 损伤参数α的确定参看式(5),假设材料初始无损伤,当材料产生宏观裂纹时有

|
假定疲劳实验数据中,同一应力下疲劳寿命N0最长的实验点对应于无初始损伤的情况,则有
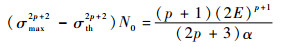
|
(15) |
由式(15)可确定损伤参数α。
参照2.1节做法,为提高参数确定的准确性,可在S-N曲线上取多组距中值疲劳寿命最远的实验点N0i(对应于无初始损伤的情况),对式(15)两边取对数并整理后有

|
(16) |
定义参数拟合均方差函数为

|
(17) |
令参数拟合均方差取极小值,即
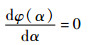
|
(18) |
至此,综合式(15)~式(18)可计算出α值,从而实现了损伤参数的单一确定。
2.3 损伤参数D0的确定如2.2节所述,在应用成组法确定材料疲劳的S-N曲线的实验中,可以假定同一应力下疲劳寿命N0最长的实验点对应于材料无初始损伤的情况。
当初始损伤度D0≠ 0时,对式(5)积分有
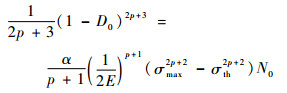
|
(19) |
在2.1节和2.2节中已经确定损伤参数α和p的前提下,利用式(19)可基于疲劳实验的S-N曲线确定材料的初始损伤度D0。
与2.1节同理,基于材料疲劳寿命的分散性和实验误差,在同样的疲劳寿命置信度下,在S-N曲线上取多组这样对应于初始损伤度D0的实验数据点(σmaxi,Ni),遵循前述的处理方法,对式(19)两边取对数有
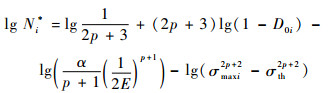
|
(20) |
定义参数拟合均方差函数为
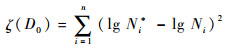
|
(21) |
令参数拟合均方差取极小值,即

|
(22) |
至此,综合式(19)~式(22)可计算在建立材料疲劳的S-N曲线的实验中,具有同样置信度的初始损伤D0。
3 应用举例本节举例说明第2节参数拟合方法的应用,选取航空工程常用的铝合金材料LC9标准板件的疲劳实验数据[15]拟合损伤参数。
超硬铝合金LC9板材标准疲劳实验的几何外形和尺寸如图 1所示,材料热处理方法为CGS1,在室温下沿轴向施加循环载荷,加载频率为160 Hz,在应力集中系数Kt分别为1、3和5时的疲劳实验数据如表 1所示。
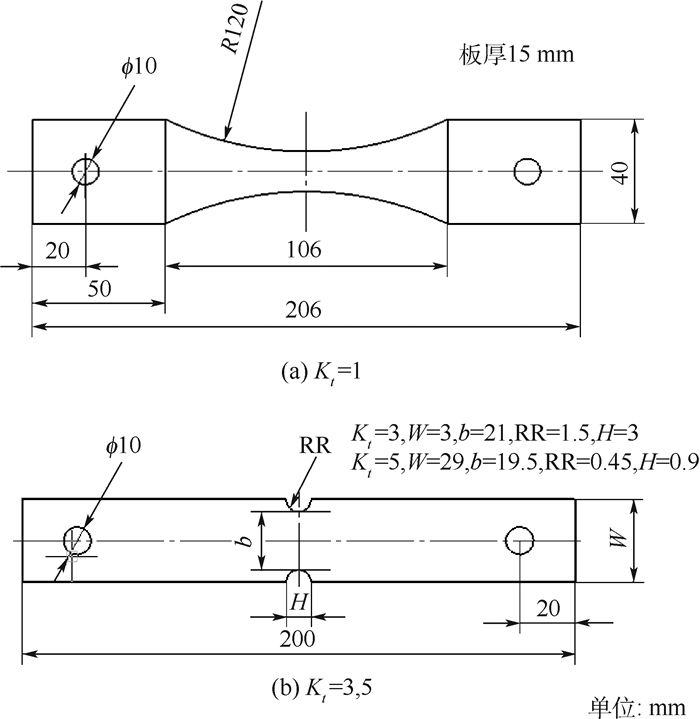
|
| 图 1 标准试样示意图 Fig. 1 Schematic diagram of standard specimen |
| Kt=1 | Kt=3 | Kt=5 | |||||
| σn/MPa | lg N | σn/MPa | lg N | σn/MPa | lg N | ||
| 270 | 4.996 4 | 147 | 4.733 5 | 98 | 4.707 0 | ||
| 221 | 5.345 6 | 98 | 5.314 1 | 78 | 5.074 4 | ||
| 196 | 5.449 2 | 88 | 5.664 5 | 67 | 5.305 7 | ||
| 156 | 5.916 7 | 76 | 5.969 8 | 60 | 5.317 8 | ||
| 130 | 6.445 8 | 70 | 5.994 1 | 57 | 5.527 3 | ||
根据表 1数据拟合S-N曲线,然后根据上述单一损伤参数确定方法分别计算p和α,所得结果如表 2所示。
| Kt | p | α |
| 1 | 1.021 | 2.505 67×10-5 |
| 3 | 1.112 3 | 4.304 6×10-4 |
| 5 | 0.389 9 | 2.867×10-4 |
分别将表 2中3套参数代入损伤演化方程式(15),并假设初始损伤为零。拟合曲线如图 2所示,可见拟合效果良好。
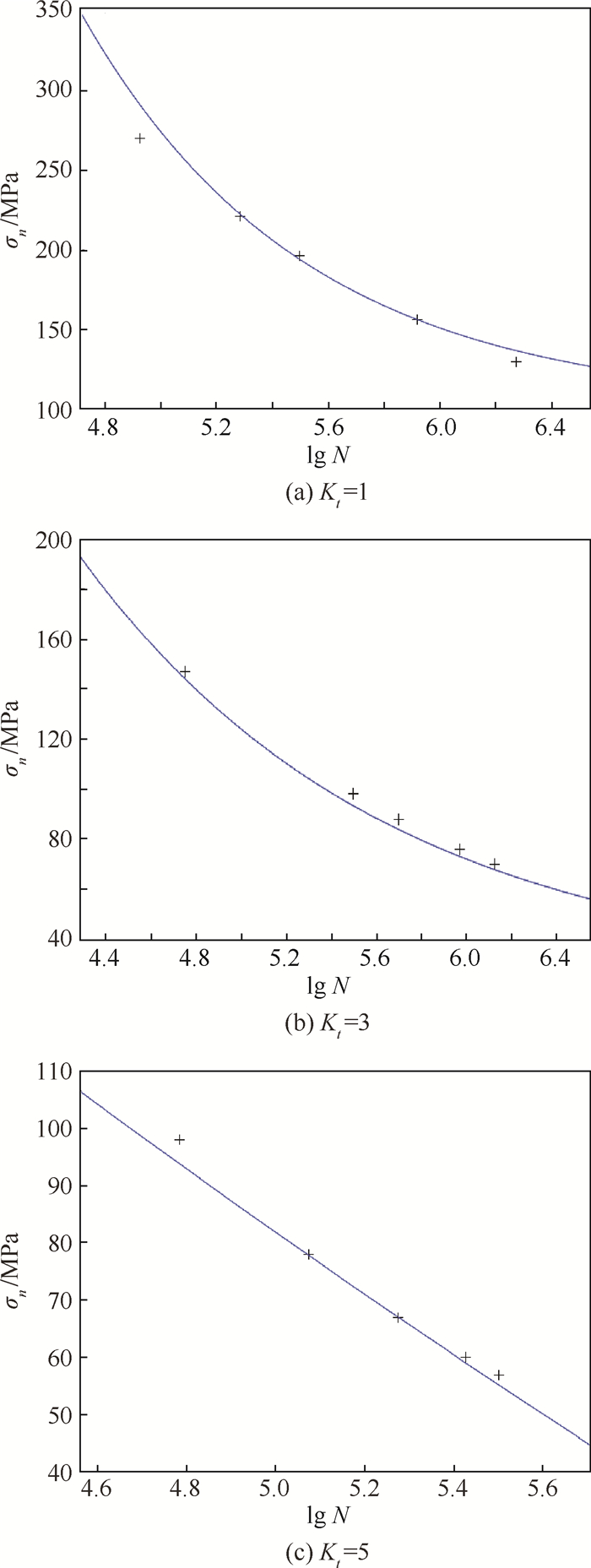
|
| 图 2 实验点与拟合曲线 Fig. 2 Test point and fitting curve |
金属材料虽然各方面的性能不尽相同,但就疲劳问题而言,损伤演化的规律性有着很强的一致性,即损伤演化可用损伤驱动力的指数函数表示。因此,常规的多参数拟合也具有较好的适用性,但是,参数越多拟合结果的不确定性就越强,可能由此造成损伤演化方程对损伤描述的偏离。一般应用中,多参数拟合是最常用的方式。
1) 本文单一损伤参数确定法旨在充分利用实验(现象/曲线)的特征,在理论框架内建立损伤参数的物理含义,不仅确定参数的方法简明,拟合的计算量小,适用性更宽泛,同时可以准确地反映金属构件的疲劳性能。
2) 本文分别基于典型结构材料的标准件(棒件/板件)疲劳实验结果,进行了损伤参数的单一确定,与实验结果相比,取得了良好的一致性,也证明了本文方法的合理性和适用性。
| [1] | ARGENTE DOS SANTOS H A, AURICCHIO F, CONTI M. Fatigue life assessment of cardiovascular balloon expandable stents:A two-scale plasticity-damage model approach[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2012, 15 : 78–92. DOI:10.1016/j.jmbbm.2012.06.011 |
| [2] |
张建宇, 费斌军. 疲劳裂纹扩展随机过程相关参数的估计[J].
北京航空航天大学学报, 1998, 24 (3): 308–310.
ZHANG J Y, FEI B J. Estimation of related parameters for stochastic process of fatigue crack propagation[J]. Journal of Beijing University of Aeronautics and Astronautics, 1998, 24 (3): 308–310. (in Chinese) |
| [3] | ZHANG L, LIU X S, WANG L S, et al. A model of continuum damage mechanics for high cycle fatigue of metallic materials[J]. Transactions of Nonferrous Metals Society of China, 2012, 22 (11): 2777–2782. DOI:10.1016/S1003-6326(11)61532-X |
| [4] |
曾春华, 邹实践.
疲劳分析方法及应用[M]. 北京: 国防工业出版社, 1991.
ZENG C H, ZOU S J. Fatigue analysis method and appliction[M]. Beijing: National Defense Industry Press, 1991. (in Chinese) |
| [5] |
张明, 王珉, 左敦稳. TC4钛合金微动疲劳特性的研究[J].
机械设计与制造, 2002 (1): 12–13.
ZHANG M, WANG M, ZUO D W. Study on the fretting fatigue properties of TC4 titanium alloy[J]. Journal of Mechanics, 2002 (1): 12–13. (in Chinese) |
| [6] |
杨锋平, 孙秦, 罗金恒, 等. 一个高周疲劳损伤演化修正模型[J].
力学学报, 2012, 44 (1): 140–147.
YANG F P, SUN Q, LUO J H, et al. A corrected damage law for high cycle fatigue[J]. Acta Mechanica Sinica, 2012, 44 (1): 140–147. (in Chinese) |
| [7] | SHANG D G, SUN G Q, DENG J, et al. Nonlinear cumulative damage model for multi-axial fatigue[J]. International Journal of Fatigue, 2006, 1 (3): 265–269. |
| [8] |
张行, 崔德渝, 孟庆春, 等.
断裂与损伤力学(第二版)[M]. 北京: 北京航空航天大学出版社, 2009: 318-348.
ZHANG X, CUI D Y, MENG Q C, et al. Fracture and damage mechanics(2nd Edition)[M]. Beijing: Beihang University Press, 2009: 318-348. (in Chinese) |
| [9] |
彭艳, 李浩然. 考虑附加强化效应的多轴高周疲劳损伤演化模型[J].
机械工程学报, 2015, 51 (16): 135–142.
PENG Y, LI H R. Multiaxial high cycle fatigue damage evolution model including additional hardening effect[J]. Journal of Mechanical Engineering, 2015, 51 (16): 135–142. (in Chinese) |
| [10] | LI D L, CHOW C L. A damage mechanics approach to fatigue assessment in offshore structures[J]. International Journal of Damage Mechanics, 1993, 1 (2): 385–405. |
| [11] |
徐小兵. 表面有横向裂纹的抽油杆寿命估算[J].
石油机械, 1993, 21 (5): 29–33.
XU X B. Life estimation of sucker rod with transverse cracks on the surface[J]. Journal of Petroleum Machinery, 1993, 21 (5): 29–33. (in Chinese) |
| [12] |
袁熙, 李舜酩. 疲劳寿命预测方法的研究现状与发展[J].
航空制造技术, 2005 (12): 80–84.
YUAN X, LI S M. Research status and development of forecast method of fatigue life[J]. Aeronautical Manufacturing Technology, 2005 (12): 80–84. DOI:10.3969/j.issn.1671-833X.2005.12.016 (in Chinese) |
| [13] |
詹志新, 佟阳, 李彬恺, 等. 考虑冲击缺陷的钛合金板的疲劳寿命预估[J].
航空学报, 2016, 37 (7): 2200–2207.
ZHAN Z X, TONG Y, LI B K, et al. Fatigue life prediction for titanium plate considering impact defect[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (7): 2200–2207. (in Chinese) |
| [14] | WAN H L, WANG Q Z, ZHANG Z. Anisotropic elastoplastic damage mechanics method to predict fatigue life of the structure[J]. Advances in Materials Science and Engineering, 2016, 2016 : 7128347. |
| [15] |
吴学仁.
飞机结构金属材料力学性能手册[M]. 北京: 航空工业出版社, 1996: 55-100.
WU X R. Manual of metal material mechanics performance in plane structure[M]. Beijing: Aviation Industry Press, 1996: 55-100. (in Chinese) |



